基于微球透鏡遠場超分辨率成像方法研究
林巧文,楊春花,劉紅梅,康占成
(1.山西大同大學 固體物理研究所,大同 037009;2.山西大同大學 物理與電子科學學院,大同 037009)
引 言
在物體結構測量時,有非光學探測和光學測量方式,其中光學測量技術因為具有非接觸、測量速度高、系統(tǒng)結構簡單等優(yōu)點被廣泛地應用[1-4]。隨著納米技術的快速發(fā)展,對成像系統(tǒng)的空間分辨率的要求越來越高。由于攜帶物體高頻細節(jié)信息的倏逝波沿著物體表面按指數(shù)衰減,在波長量級的距離內很快衰減為0,導致成像系統(tǒng)在遠場受到衍射效應的限制。由于倏逝波攜帶了物體的更多高頻細節(jié)信息,利用在近場掃描探測的方法可以獲得倏逝波實現(xiàn)超越衍射極限的分辨率,如近場掃描光學顯微鏡和受激發(fā)射損耗熒光顯微鏡[5-6]。1972年,ASH等人通過近場掃描顯微鏡,獲得了超分辨率顯微成像,由于其是通過探針在近場區(qū)域逐點進行掃描測量物體的信息,耗時長,無法實時地成像[5]。2000年,PENDRY通過介電常數(shù)和磁導率均為負數(shù)的材料制成了完美透鏡將倏逝波放大,實現(xiàn)了在近場突破衍射極限的成像[7]。2004年,美國加州大學ZHANG團隊利用銀板制成了近場透鏡[8],為了實現(xiàn)遠場超分辨率成像,2007年,該團隊首先利用負折射率材料制成的超級透鏡將倏逝波放大,然后利用光柵的頻移特性將倏逝波轉換成傳輸波,實現(xiàn)遠場超分辨率成像[9],同年,他們使用雙曲透鏡實現(xiàn)了遠場超分辨率成像,其結構必須嚴格設計,在實際應用時也受到了限制[10]。近年來,利用微球結合普通的光學顯微鏡在遠場實現(xiàn)了突破衍射極限的分辨率,有結構簡單、成本低等優(yōu)點[11-21],吸引了許多國內外眾多學者的關注。作者通過折射率為2、半徑為26.5μm的鈦酸鋇微球與光學顯微鏡相結合,實現(xiàn)對藍光光盤的遠場超分辨成像。
1 理論分析
1.1 普通光學顯微鏡的極限分辨率
普通光學顯微成像系統(tǒng)記錄過程的簡化模型如圖1所示。(x,y)為物體所在的平面,垂直于物平面的z軸為光的傳播方向,物平面距顯微物鏡面的距離為d1,顯微物鏡面的距離與像面的距離為d2,d1和d2滿足物像關系。
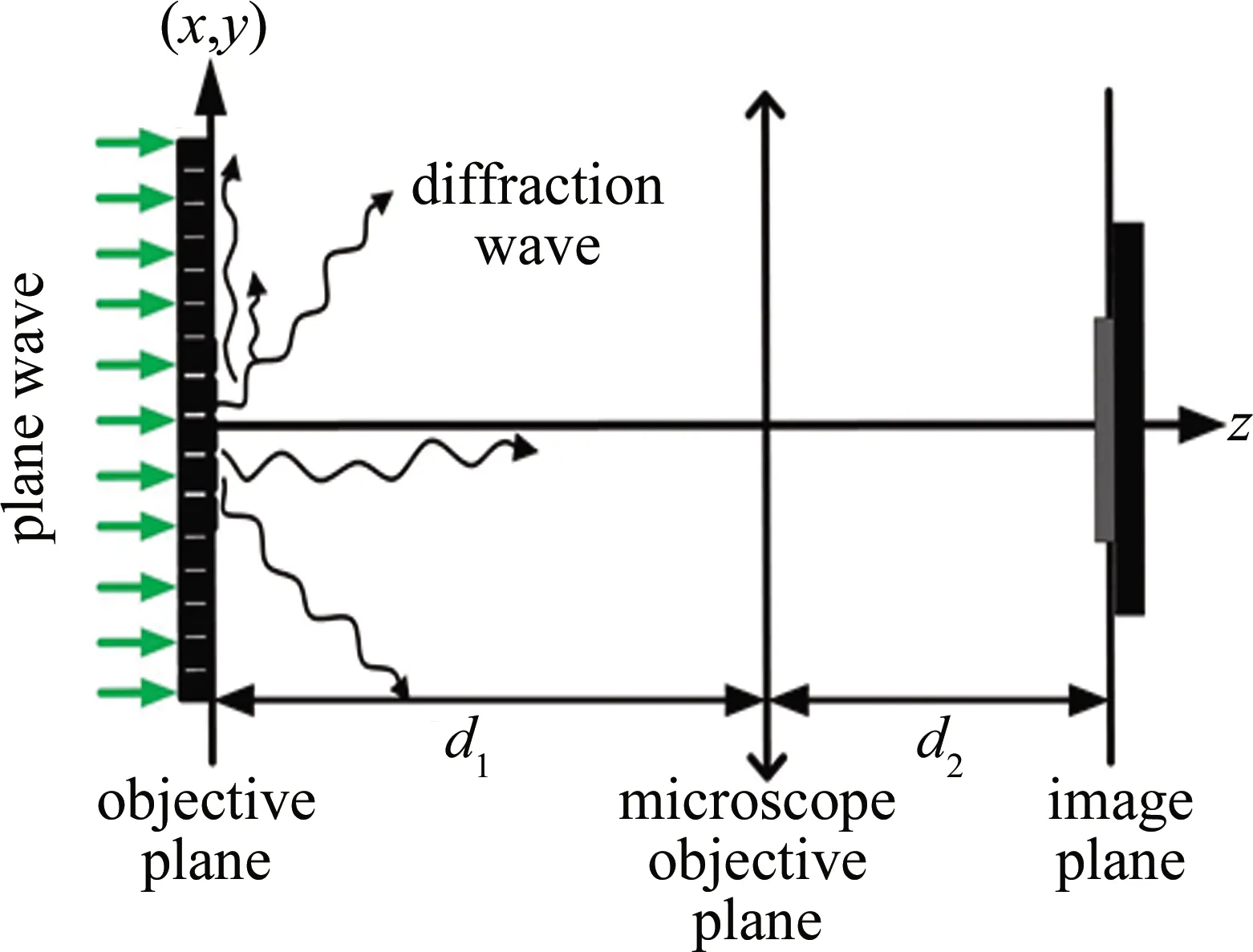
Fig.1 The simplified model of the optical microscopic imaging system
當用一束平面光波垂直照射被測物體后,在物體表面,即z=0處,物體光波場的分布為[18-22]:
u(x,y,0)=
(1)
式中,(kx,ky)為沿著x,y方向的空間波矢分量。
在空氣中傳播距離d1后的物體光波場為:
exp[i(kxx+kyy+kzd1)]dkxdky
(2)
式中,kz2=k02-kx2-ky2,k0為不同方向疊加的空間波矢,k0=2π/λ為光波在傳播方向的波數(shù),kz為沿著z方向的空間波矢分量,λ為照明光波波長。
(2)式表示物體光波場是由空間頻率為(kx,ky)的無窮多組平面波沿不同傳播方向的疊加,每組平面波可表示為[21-22]:
U(kx,ky,0)exp[i(kxx+kyy+kzz)]
(3)
當k02>kx2+ky2時,傳播距離d1后其光場分布為:
U(kx,ky,0)exp[i(kxx+kyy)]×
(4)
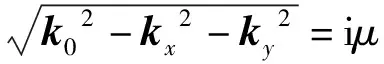
U(kx,ky,0)exp(-μd1)exp[i(kxx+kyy)]
(5)
此稱為倏逝波,隨著傳播距離d1的增加,其振幅按指數(shù)規(guī)律衰減,當傳播距離大于一個波長λ時很快衰減為0。由于d1?λ,倏逝波沒有達到顯微物鏡面,不能參與遠場成像。成像系統(tǒng)頻譜分布如圖2所示。
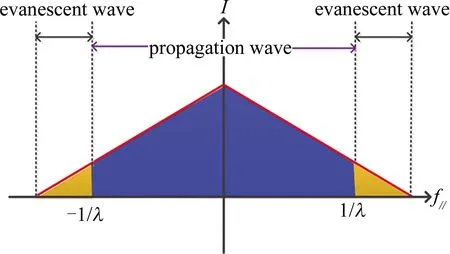
Fig.2 The spectrum distribution of the imaging systems
能參與遠場成像的傳輸波被限制為k02>kx2+ky2,其最大的橫向空間波矢為:
k∥,max=k0
(6)
因此,遠場成像的橫向最高空間頻率被限制在[7,20-21]:
(7)
如圖2所示,橫向頻率小于1/λ時,為傳輸波;橫向頻率大于1/λ時,為倏逝波,沿著傳播方向衰減,在探測器處無法探測到。因此遠場成像系統(tǒng)的空間分辨率為[7,20]:
(8)
因此普通光學顯微鏡的極限分辨率為λ/2。由于倏逝波攜帶了納米結構樣品的更多亞波長細節(jié)信息,為了在遠場實現(xiàn)超越衍射極限的分辨率,需要收集到倏逝波。
1.2 基于微球的超分辨率成像
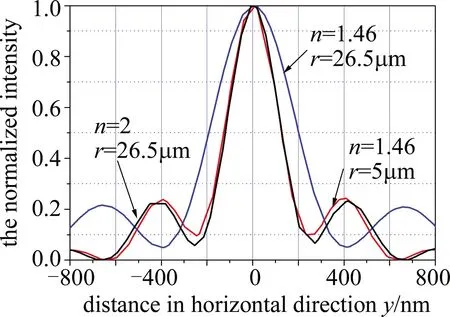
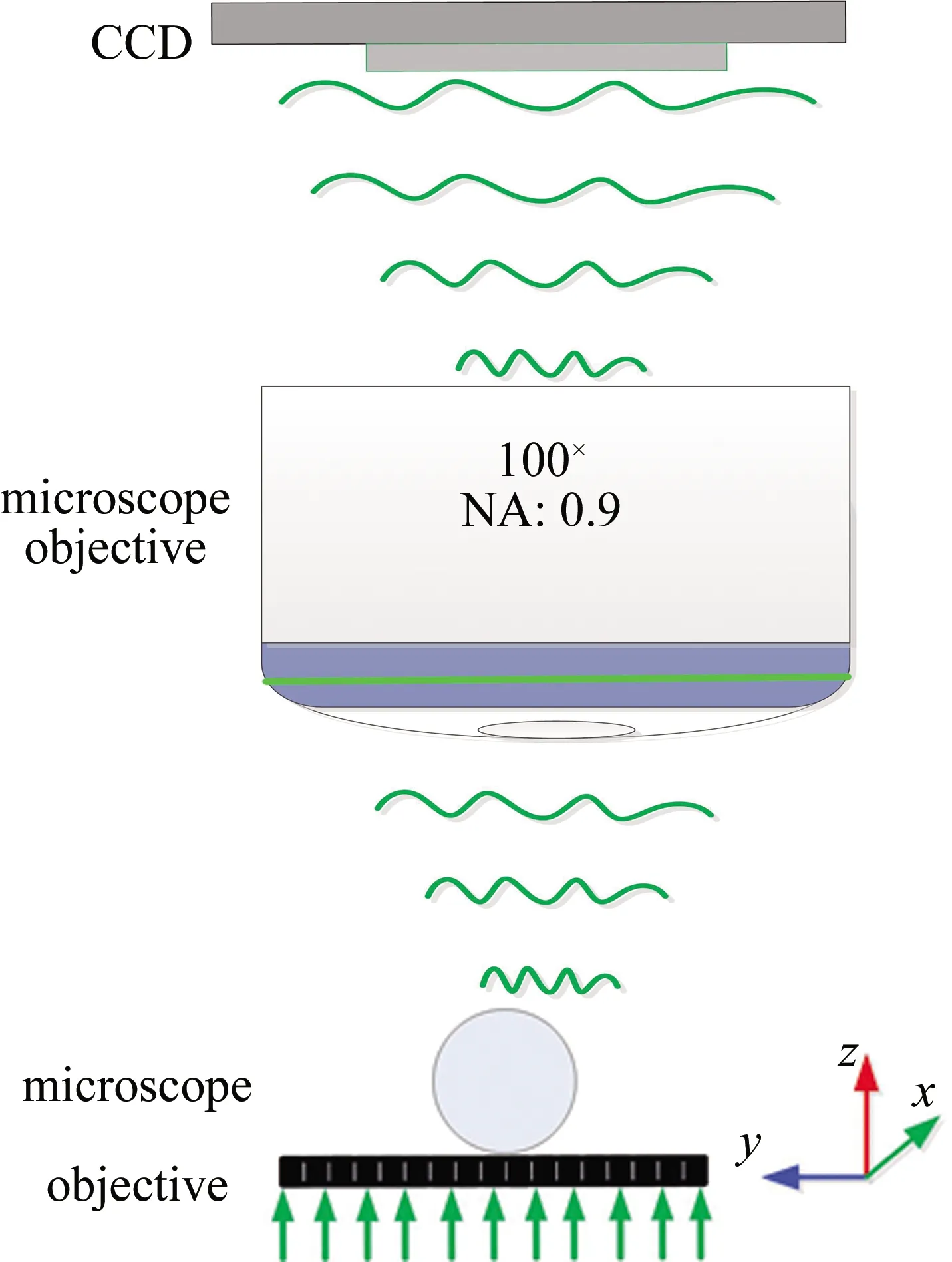
當橫向波矢量滿足k02 Fig.3 The simplified model of the microsphere-based optical microscopic imaging system 微球中,分解到u和w方向的波矢量分別為ku和kw,且滿足: ku2+kw2=n2k02 (9) 當倏逝波入射到微球時,通過Snell定量可知,微球內沿著u方向的波矢量ku可以表示為[18-19]: ku2=kx2cos2θ+kz2sin2θ= (10) (11) (12) 物體散射后產生的倏逝波在微球里傳播與微球的半徑和折射率有關,且需滿足(12)式。 由(12)式可知,通過微球后可獲得最大的空間頻率為: (13) 微球光學顯微成像系統(tǒng)可分辨的最小距離為: (14) 由(14)式可知,微球光學顯微成像系統(tǒng)可分辨的最小距離與微球的折射率和半徑有關。由于n2R-2λ-(R-4λ)>0,由(14)式可得: (15) 利用COMSOL Multiphysics軟件來分析微球的光納米噴射特性。用波長為400nm的平行光照射折射率為1.46、半徑分別為5μm和26.5μm的二氧化硅微球以及折射率為2、半徑為26.5μm的鈦酸鋇微球后,產生的光納米噴射結果分別如圖4a、圖4b和圖4c所示。分別在其光納米噴射光斑的最大光強處作出沿著豎直方向上的強度分布如圖5所示。仿真結果表明,微球對平行光產生光納米噴射的作用,且其光納米噴射光斑的半徑小于λ/2;從仿真結果圖4a、圖4b和圖5可以看出,對相同折射率不同半徑的微球,光噴射的尺寸隨著微球半徑的增大而增大;從圖4b、圖4c和圖5可以看出,對相同半徑不同折射率的微球,光噴射的尺寸隨著折射率的增大而減小,說明微球具有收集倏逝波的作用。當成像系統(tǒng)中加入微球后可以使其分辨率突破衍射極限。 Fig.5 The intensity distribution of the photonic nanojet in the maximum intensity along the vertical direction 將鈦酸鋇微球與光學顯微鏡組合成遠場超分辨率成像系統(tǒng),其實驗光路如圖6所示。所用的光學顯微鏡為OLYPUS BX51,顯微物鏡的數(shù)值孔徑(numerical cperture,NA)為0.9,放大倍數(shù)為100×。實驗中利用反射模式,中心波長為600nm的鹵素燈作為光源;顯微鏡的極限分辨率為406.6nm;線寬為200nm、間隔為100nm的藍光光盤作為被測對象。通過掃描電子顯微鏡(scanning electron microscopy,SEM)測得的藍光光盤的結構如圖7a所示。由于藍光光盤尺寸小于顯微鏡的極限分辨率,直接在顯微鏡下觀察不到藍光光盤的細節(jié)信息如圖7b所示。從仿真結果圖4可知,折射率為1.46、半徑為5μm的二氧化硅微球與折射率為2、半徑為26.5μm的鈦酸鋇微球產生的光噴射尺寸相近,且都小于折射率為1.46、半徑為26.5μm的二氧化硅微球。為了得到大視場的超分辨率成像,實驗研究中所選用的微球參量為折射率為2、半徑為26.5μm的鈦酸鋇微球,微球直接在顯微鏡下的成像如圖7c所示。在實驗前將藍光光盤上面的保護膜去掉,并將微球用去離子水稀釋后,滴到藍光光盤的表面上,等水蒸發(fā)完后,將微球半浸沒在無水的乙醇溶液中。 Fig.6 The light path diagram of the microsphere-based far-field super-resolution imaging system 通過微球結合光學顯微鏡的成像系統(tǒng)得到藍光光盤的像如圖7d所示。圖7e為圖7d方框區(qū)域的放大圖。從圖7e可以看出,藍光光盤的細節(jié)信息被清晰分辨。實驗結果說明,實驗中加入微球后可將攜帶物體細節(jié)信息的倏逝波轉換成傳輸波參與遠場成像,實現(xiàn)了樣品的超分辨率成像。 Fig.7 The imaging results of the blu-ray disc 針對對微納結構元器件結構檢測精度高、速度快的需求,設計了一套基于微球與傳統(tǒng)光學顯微鏡相結合的遠場超分辨率成像系統(tǒng),并分析了該成像系統(tǒng)的實現(xiàn)遠場超分辨率成像的物理機理。利用微球對平行光產生光納米噴射的特性,將攜帶物體高頻細節(jié)信息的倏逝波轉換成傳輸波,然后傳輸波通過顯微物鏡在光電探測器處成像實現(xiàn)遠場超分辨成像;實驗中實現(xiàn)了對藍光光盤的遠場超分辨率成像,獲得了100nm的分辨率。由于微球具有球對稱性,其可以實現(xiàn)各個方向的超分辨率成像。 該成像方法具有系統(tǒng)結構簡單、成本低等優(yōu)點,可以應用于對微納元件結構的檢測、光刻技術、生物醫(yī)學等領域。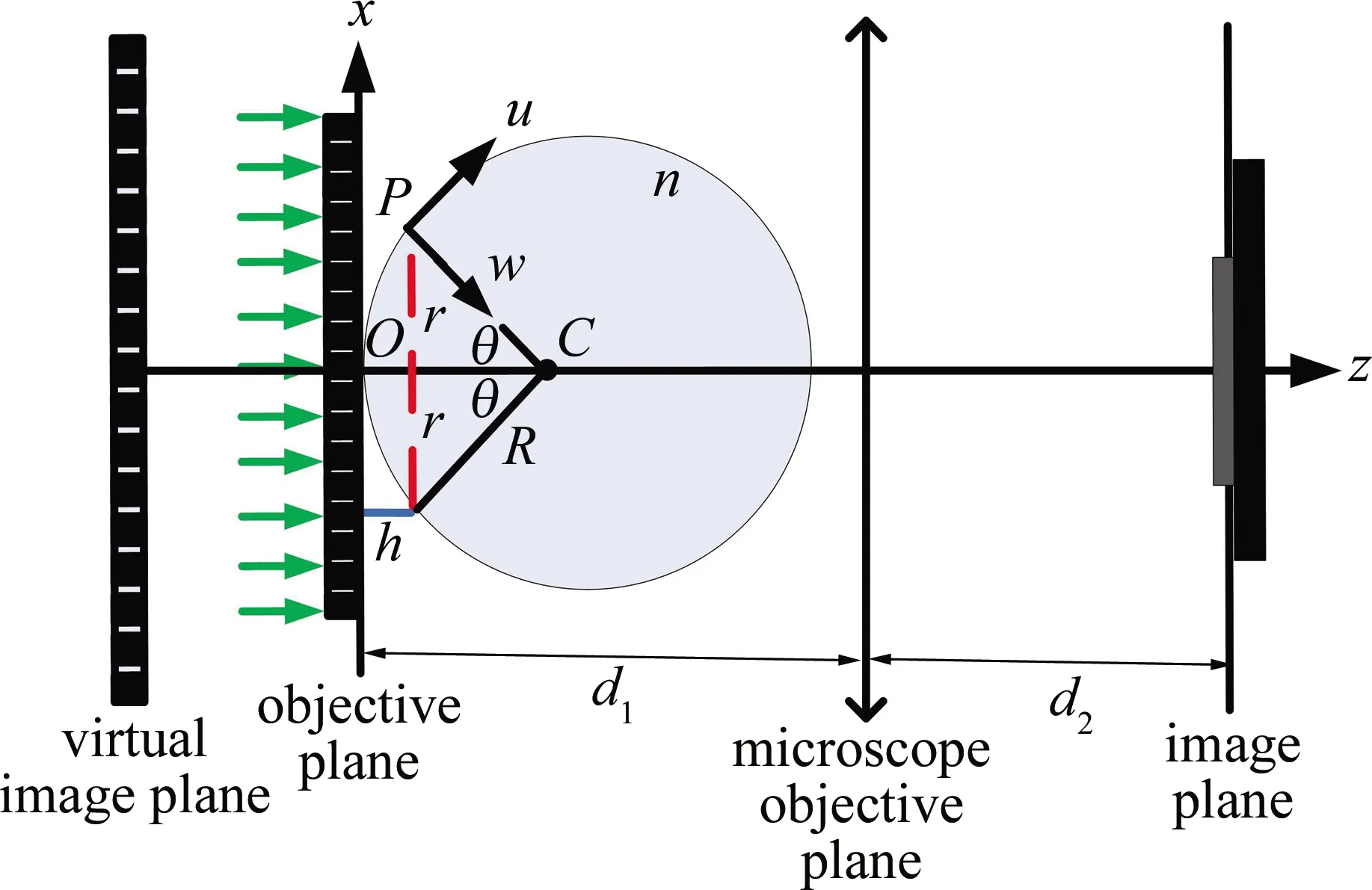

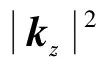
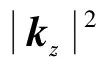
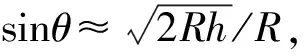
2 仿真研究
3 基于微球超分辨率成像的實驗研究

4 結 論

