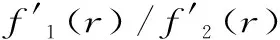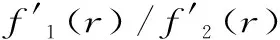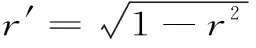Toader型平均的兩個最佳不等式*

張 帆

(湖州職業技術學院 建筑工程學院， 浙江 湖州 313000)

一、研究背景

設0

第一類和第二類完全橢圓積分滿足下列微分公式和Landen恒等式[1]474-475:

且第一類完全橢圓積分κ(r)在區間(0,1)內嚴格單調遞增,第二類完全橢圓積分ε(r)在區間(0,1)內嚴格單調遞減.

設x,y>0和x≠y.則將調和平均H(x,y),幾何平均G(x,y),算術平均A(x,y),Toader平均T(x,y)[2]358-368,正弦平均Msin(x,y)和雙曲正切平均Mtanh(x,y)[3]1 071-1 092分別定義如下:

(1)

(2)

(3)

最近,Toader平均,正弦平均和雙曲正切平均與其他二元經典平均的比較得到了國內外學者的深入研究，在特殊情形下,發現了許多關于完全橢圓積分,三角函數和雙曲函數的重要不等式.

有人證明了λ=3/2和μ=ln2/ln(π/2)=1.534 9L是使得雙向不等式

Mλ(x,y)

還有人證明了雙向不等式

A(x,y)

(4)

對所有x,y>0和x≠y成立[3]1 078.

顯然,雙向不等式

H(x,y)

(5)

對所有x,y>0和x≠y成立.

從不等式(4)和(5)可推得

H(x,y)

(6)

對所有x,y>0和x≠y成立.

根據不等式(6),本文的主要結果為以下兩個定理:

定理1雙向不等式

對所有x,y>0和x≠y成立的充分必要條件是:α1≤4sin2(1)/π2=0.286 9L和β1≥9/14.

定理2雙向不等式

對所有x,y>0和x≠y成立的充分必要條件是:α2≤4tanh2(1)/π2=0.235 0L和β2≥9/16.

二、引 理

為證明本文的主要結果,需要以下引理:

引理1對-∞

也在(a,b)內單調上升(下降);如果f′(x)/g′(x)的單調性是嚴格的,則結論中的單調性也是嚴格的[3]10.

引理3冪級數公式:

其中,Bn是Bernoulli數[7]4 874-4 888.

引理4雙向不等式

對所有n∈+成立,其中Bn是Bernoulli數[8]1-14.

引理5(1)函數r[κ(r)-ε(r)]/r2在區間(0,1)內是嚴格單調遞增的，且值域為(π/4,1)[1]70.(2)函數r[ε2(r)-r′2κ2(r)]/r4在區間(0,1)內是嚴格單調遞增的，且值域為(π2/32,1)[1]70.

引理6函數rε(r)[(1+r2)ε(r)-r′2κ(r)]/r2在區間(0,1)內是嚴格單調遞減的，且值域為(2,3π2/8).

證明:設

φ(r)=ε(r)[(1+r2)ε(r)-r′2κ(r)]/r2.

簡單計算可得:

(7)

(8)

所以,引理6容易從引理5及等式(7)和(8)得到.

引理7函數

在區間(0,1)內嚴格單調遞增，且值域為(7/3,2/sin2(1)).

證明:簡單計算可得:

(9)

(10)

其中,

λ1(r)=3rsec2(r)-r3sec2(r)-3tan(r)+r2tan(r)-2r3.

由引理3得到:

(11)

其中,

(12)

由引理4和等式(12)得到:

(13)

其中,

?1(n)=12n(22n+2-1)(22n-1-1)-π2(n-1)(22n-1)(22n+1-1)>

22n[22n+1((12-π2)n+π2)-3((18-π2)n+π2)]+(12-π2)n+π2>

22n[22n+1((12-π2)n+π2)-3((18-π2)n+π2)]+2n+π2.

(14)

應用二項式展開式,可得:

22n+1((12-π2)n+π2)-3((18-π2)n+π2)>

2(1+2n)((12-π2)n+π2)-3((18-π2)n+π2)=

4(12-π2)n2+5(π2-6)-π2>132-7π2>0,

(15)

且對所有n≥2成立.

所以,引理7容易從等式(9)～(11)和不等式(13)～(15)得到.

引理8函數

在區間(0,1)內是嚴格單調遞增的,且值域為(8/3,2coth2(1)).

證明:函數μ(r)可變為：

(16)

由雙曲正弦函數和雙曲余弦函數的冪級數展開公式可得:

r2sinh(3r)+sinh(3r)+r2sinh(r)+sinh(r)+4r3cosh(r)-4rcosh(r)=

(17)

(18)

設

(19)

則由等式(16)～(18)得到:

(20)

(21)

其中,

ω(n)=32n+1[(4n+7)32n+4-2(192n3+536n2+356n+9)]-(48n2+148n+111).

(22)

應用二項式展開式可得:

(4n+7)32n+4-2(192n3+536n2+356n+9)>

2 208n3+3 464n2-388n+549>0.

(23)

由等式(22)和不等式(23)得:

ω(n)>32n+1(2 208n3+3 464n2-388n+549)-(48n2+148n+111)>3(2 208n3+3 464n2-388n+549)-(48n2+148n+111)=6 240n3+9 320n2-1 876n+1 629>0,

(24)

且對所有n∈成立.

根據引理2和等式(19)～(21)協同不等式(24)導致的結論是:函數μ(r)在區間(0,1)內嚴格單調遞增.注意到,

(25)

所以,引理8容易從等式(25)和函數μ(r)的單調性得到.

三、主要結果的證明

定理1的證明:根據二元平均H(x,y),Msin(x,y)和T[A(x,y),G(x,y)]是對稱的且一階齊次,不失一般性,假設x>y>0,r=(x-y)/(x+y)∈(0,1).則由等式(1)和(2)得到:

(26)

設f1(r)=4ε2(r)/(π2r′4)-1和f2(r)=r2/[r′4sin2(r)]-1.簡單計算得到:

f1(0+)=f2(0)=0,f(r)=f1(r)/f2(r),

(27)

(28)

其中,函數λ(r)定義在引理7.

(29)

定理2的證明:根據二元平均H(x,y),Mtanh(x,y)和T[A(x,y),G(x,y)]是對稱的且一階齊次,不失一般性,假設x>y>0,r=(x-y)/(x+y)∈(0,1).則從等式(1)得到:

(30)

設f1(r)=4ε2(r)/(π2r′4)-1和f3(r)=r2/[r′4tanh2(r)]-1.則簡單計算得到:

f1(0+)=f3(0)=0,g(r)=f1(r)/f3(r),

(31)

(32)

其中,函數μ(r)定義在引理8.

(33)

根據定理1和定理2,得到推論如下:

推論1雙向不等式