反雙紐線三角函數的兩個最佳不等式*
何曉紅, 李少云
(1.衢州廣播電視大學 教務處, 浙江 衢州 324000; 2.溫州廣播電視大學 教師教學發展中心, 浙江 溫州 325000)
一、研究基礎
反雙紐線正弦和反雙紐線雙曲正弦函數[1]496-505 [2]259的定義分別為:
和
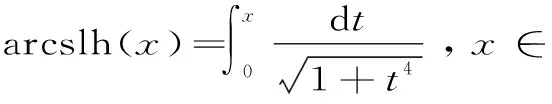
為論述方便,對這兩個函數的極限值記為:[2]259
和
其中,
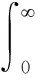
是經典伽馬函數[3]1-17,并且
是第一類完全橢圓積分[4]1-10.對實數a,b,c∈且c≠0,-1,-2….將高斯超幾何函數F(a,b;c;x)定義為:
其中,當a≠0時,(a,0)=1;當n∈≡{k:k是正整數}時,
是移位階乘函數.
另一對反雙紐線三角函數,即反雙紐線正切函數和反雙紐線雙曲正切函數分別定義為[5]77-94:
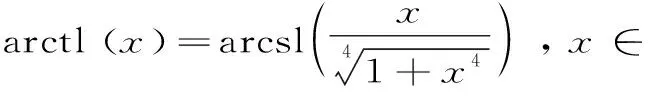
和
近幾年,反雙紐線三角函數的性質和不等式引起了國內外許多研究者的關注,并取得了豐碩成果.例如:陳超平建立了反雙紐線三角函數的Wilker和Huygens型不等式[6]673-684
對所有0<|x|<1成立.
還有學者給出了反雙紐線三角函數之間的不等式[7]1-14
arctl(x) 對所有x∈(0,1)成立. 本文的主要目的是發現并證明最佳參數α1,α2,β1,β2∈(0,1),使得雙向不等式 α1arcsl(x)+(1-α1)arcslh(x) α2arctlh(x)+(1-α2)arctl(x) 對所有x∈(0,1)成立. 為證明本文的主要結果,需要一些反雙紐線三角函數的基本知識和三個引理. 我們記下面兩個反雙紐線函數值為: 根據反雙紐線三角函數的定義和求導法則,我們容易得到它們的導數公式: 引理1設x1,x2∈且x1 在區間(x1,x2)內也是(嚴格)遞增(遞減)的[8]10. 引理2函數 φ(x)=(1+x4)3/2+(1-x4)3/2-2 證明:對函數φ(x)求導,可得 (1) 對所有x∈(0,1)成立.注意到: (2) 所以,引理2容易從式(1)和式(2)得到. 引理3函數 φ(x)=(1+x4)7/4+(1-x4)7/4-2 證明:對函數φ(x)求導,可得 (3) 對所有x∈(0,1)成立.注意到: (4) 所以,引理3容易從式(3)和式(4)得到. 下面給出本文的主要結果并證明之. 定理1雙向不等式 α1arcsl(x)+(1-α1)arcslh(x) (5) 對所有x∈(0,1)成立,當且僅當α1≤(1-σ)/(ω-σ)=0.190 0L和β1≥1/2. 證明:不等式(5)可以寫成: (6) 簡單計算可得: (7) (8) 其中,φ(x)定義在引理2. (9) 定理2雙向不等式 α2arctlh(x)+(1-α2)arctl(x) (10) 對所有x∈(0,1)成立,當且僅當α2≤(1-τ)/(κ-τ)=0.108 9L和β2≥1/2. 證明:不等式(10)可寫成: (11) 簡單計算可得: (12) (13) 其中,φ(x)定義在引理3. (14) 根據定理1和2,我們可得到如下最優不等式: 定理3雙向不等式 對所有0<|x|<1成立. 自17世紀末以來,反雙紐線三角函數得到了深入的研究,許多國內外數學工作者取得了豐碩的研究成果.本文通過對四個反雙紐線三角函數的比較,推得了反雙紐線正弦函數和反雙紐線雙曲正弦函數,以及反雙紐線正切函數和反雙紐線雙曲正切函數凸組合的兩個精確不等式,這對進一步研究反雙紐線三角函數之間的關系具有重要的理論意義.二、三個引理
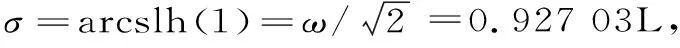
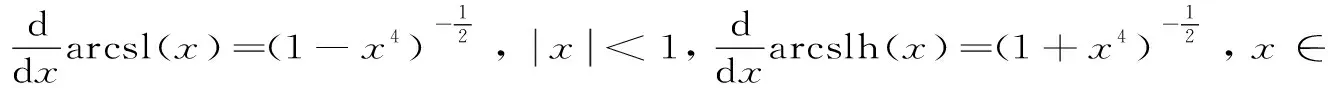
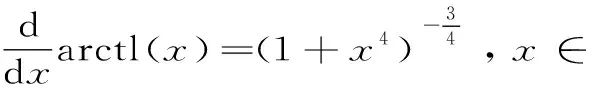
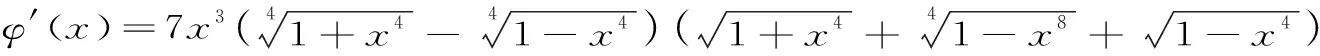
三、主要結果
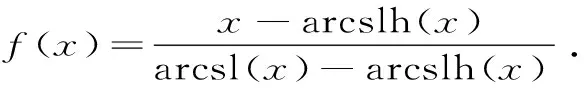
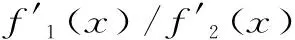
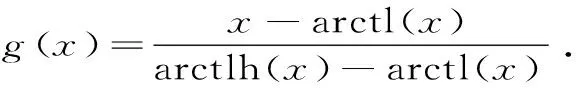
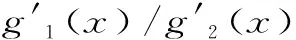
四、結 語

