2021年全國乙卷理科第21題解法探究與背景溯源

安徽 劉守文

一、試題呈現

(2021·全國乙卷理·21)已知拋物線C:x2=2py(p>0)的焦點為F，且F與圓M:x2+(y+4)2=1上點的距離的最小值為4．

(1)求p；

(2)若點P在M上，PA,PB是C的兩條切線，A,B是切點，求△PAB面積的最大值．

二、試題第(2)問解法探究

本題的第(2)問求△PAB面積的最大值，是高考圓錐曲線常考的面積問題.考查學生對圓錐曲線基本解題方法、技能的掌握和解題基本思想的領悟，側重學生分析和解決問題的能力.本文主要針對第(2)問進行分析.

解法1：“設而不求”法

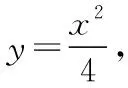
設點A(x1,y1)，B(x2,y2)，P(x0,y0)，

即x1x-2y1-2y=0，

同理可知，直線PB的方程為x2x-2y2-2y=0，

由于點P為這兩條直線公共點，

即點A,B兩點的坐標均滿足方程x0x-2y-2y0=0，

所以直線AB的方程為x0x-2y-2y0=0，

可得x2-2x0x+4y0=0，

由韋達定理可得x1+x2=2x0，x1x2=4y0，

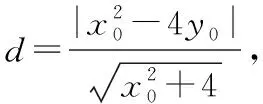
解法2：三角代換法(利用圓的參數方程)

解法3：圖形割補

如圖,設點A(x1,y1),B(x2,y2),P(x0,y0)，

過點P作PQ∥y軸,交AB于點Q，則

由解法1可知，直線AB:x0x-2y-2y0=0，與直線PQ：x=x0聯立，

下同解法1.

點評：解法1～3是典型的“設而不求”思想方法的運用，不同的是解法3將△PAB一分為二，方法處理上更加技巧.這幾種方法是高考復習中解決圓錐曲線面積問題的通性通法，考查了學生對基礎知識的掌握、基本技能的應用以及對基本思想的理解與領悟，教師教學中要注重通性通法的講解，加強對學生“四基”的針對性訓練.

解法4：三角形面積向量公式法

設點A(x1,y1)，B(x2,y2)，P(x0,y0)，

下同解法1.

解法5：向量轉化法

設點A(x1,y1)，B(x2,y2)，P(x0,y0)，

由解法1可知，直線AB：x0x-2y-2y0=0，

則直線AB與y軸交點為C,則C(0,-y0).

λy2+y1+(λ+1)y0=0 ②，

下同解法1.

三、試題結論推廣

限于篇幅，此處只證明當x2=2py(p>0)時的結論，其他形式的證明過程類似.

證明：當x2=2py(p>0)時，如圖所示，過點P作PQ∥y軸,交AB于點Q，

設點A(x1,y1)，B(x2,y2)，聯立PA,PB的方程

當|AB|為定值時，令點P到直線AB的距離為d，

四、試題數學文化背景溯源

《普通高中數學課程標準(2017年版2020年修訂)》指出: 數學文化是指數學的思想、精神、語言、方法、觀點,以及它們的形成和發展.數學的形成和發展史是數學文化的重要內容，2021年高考數學全國乙卷涉及拋物線的弦與過弦的端點的兩條切線所圍的三角形，這個三角形又常被稱為阿基米德三角形.阿基米德是古希臘偉大的數學家、物理學家，他最早用逼近的思想推出了拋物線弓形的面積,是微積分思想的先驅，享有“數學之神”的稱號.阿基米德三角形內涵豐富，在數學史上具有重要地位，其重要性質一直是高考圓錐曲線命題的熱點素材和高頻考點，是從高考命題角度對課標理念“數學文化融入數學課程”的重要體現，其出題多以隱性形式給出.筆者歸納了近些年高考全國卷試題中阿基米德三角形的常考知識點，如下表所示.

出題形式考查性質考查目標2019年全國卷Ⅲ理21題解答題阿基米德三角形頂點在準線上,則底邊恒過焦點定點、面積2018年全國卷Ⅲ理16題填空題阿基米德三角形頂點在準線上,則頂點與焦點連線與底邊垂直焦點弦斜率2006年全國卷Ⅱ理21題解答題阿基米德三角形頂點在準線上,則頂點與焦點連線與底邊垂直定值、面積最值

阿基米德三角形在高考各省自主命題中也屢有出現，在此不再一一列舉.通過歸納可以發現，試題主要運用阿基米德三角形性質考查弦長、定點(值)、軌跡、切線、面積、范圍等圓錐曲線基本知識.

五、教學啟發

笛卡兒的坐標系為數學發展插上了一對翅膀，坐標系將數與形完美地結合起來，詮釋了數學的統一美.解析幾何利用“數”的方法解決“形”的問題，通過代數運算確認幾何圖形的內在關系.圓錐曲線高考試題考查了數學運算能力，是發展數學運算核心素養的重要載體，是獲取“四基”，提高“四能”的重要途徑.對于圓錐曲線教學，有以下兩點教學啟發.

(一)注重通性通法研究

高考圓錐曲線試題具有運算量大，思維嚴謹性高的特點.教學中教師要重視通性通法的講解，重視打牢基礎知識，傳授基本解題思路及技巧，滲透基本解題思想方法，提升學生分析和解決問題的能力.如2021年全國乙卷第21題，其主要考查學生對圓錐曲線解題中最一般也是最核心的思想方法——“設而不求”思想方法的理解與掌握.教師在教學中要總結常見幾何圖形關系的代數表征，將平面幾何圖形關系“翻譯”成代數表達式.對于復雜問題，可以嘗試分解為幾個步驟，采用分步策略幫助學生理解問題.引導學生歸納、總結一般思路、一般規律.通過數學運算理清思路、拓展思維，發展數學核心素養.

(二)注重高考試題背景研究