從一道高考題談試題命制
山東 孫 浩
圓錐曲線問題是歷年高考的主力軍,也是高三復習備考的重頭戲.但是在高三復習備考中卻體現為用時多、收效低的特點,學生在歷次考試中都作答不理想,試題得分率極低.下面筆者基于多年參與統考試題命制工作,從試題命制的角度談談看法,期望能給讀者以啟迪.
1.高考試題為命制試題提供優秀藍本
命制試題經常會參考往年全國卷及各省市的高考試題,高考試題出題嚴謹,無論是考查的知識點、考查能力,還是命題角度都能給命制試題提供好的思路和想法,因此在命制試題時經常以高考試題為藍本進行改編命制.
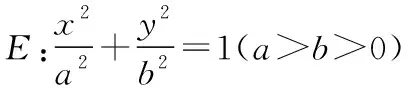
(1)求橢圓E的方程;
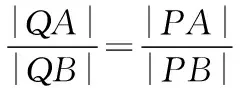

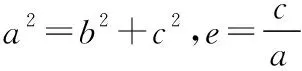
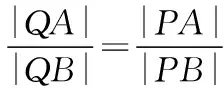
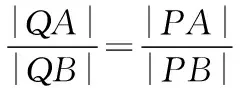

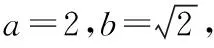
(2)當直線l與x軸平行時,設直線l與橢圓相交于C,D兩點.

∴Q點在y軸上,可設Q點的坐標為(0,y0).
當直線l與x軸垂直時,設直線l與橢圓相交于M,N兩點,

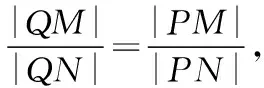
∴若存在不同于點P的定點Q滿足條件,則Q點的坐標只可能為Q(0,2).
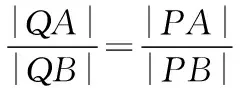
當直線l的斜率不存在時,由上可知,結論成立.
當直線l的斜率存在時,可設直線l的方程為y=kx+1,A,B的坐標分別為(x1,y1),(x2,y2).
其判別式Δ=16k2+8(2k2+1)>0,
∴kQA=-kQB,
∴∠PQA=∠PQB.
過點A,B向y軸分別作垂線AM,BN,垂足分別為M,N,則Rt△QMA∽Rt△QNB,
又Rt△PMA∽ Rt△PNB,
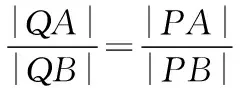
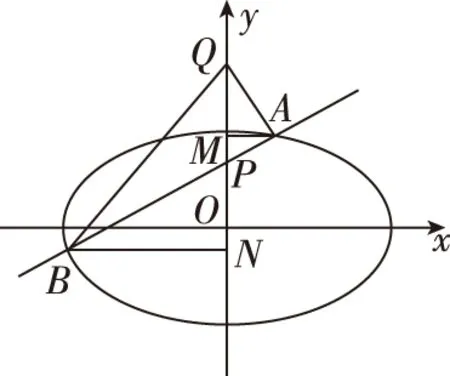
從這道高考試題的分析和解答過程可以看出,本題設置了求橢圓方程和兩直線的斜率關系兩個落腳點,試題命制圍繞這兩個落腳點而展開.下面談談依據這兩個落腳點如何進行試題命制的.
2.以求橢圓的標準方程為落腳點進行試題命制
橢圓的標準方程含有a,b兩個量,這兩個量與c,e有直接關系,因此在試題命制中,一般是圍繞a,b,c,e四個量來建構兩個方程,思考這幾個量與哪些知識點有關聯,如何建立聯系,圍繞其中一個或幾個量進行問題設計、建構關系式,從而達到考查有關知識和能力的目的.
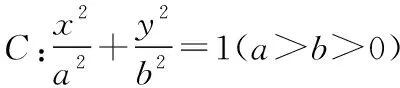

(1)求橢圓C的方程;
(2)略.
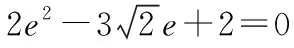
【詳解】(1)由題意可得,
∴a=2.

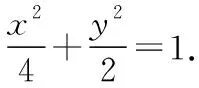

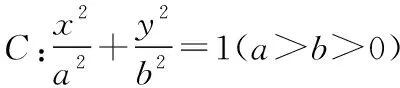
(1)求橢圓C的方程;(2)略.
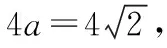
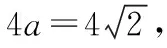

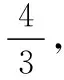
解得c=1或c=2(舍去),
∴b2=1,
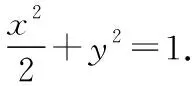
通過上面兩道試題的命制,發現以求橢圓的標準方程為落腳點的試題命制,先確立要求的橢圓標準方程是什么,然后根據a,b,c,e的具體值,從這些值中選取兩個,圍繞這兩個值結合其他相關知識來設計問題,完成試題的命制.
3.以斜率為落腳點來命制考查直線與圓錐曲線位置關系試題
試題命制就是尋找一個問題有什么不同的說法,把這個問題延伸拓展一下,向前走幾步或者向后退一退,尋找合適的說法進行化歸與轉化,把舊問題轉化為新問題、新情境,實現新瓶裝老酒,靈活考查知識、能力和數學核心素養.

3.1 直接以斜率之間的關系來命制試題
命制試題時,考慮學生對知識掌握的程度,有時需要降低試題難度,直接給出斜率之間的關系,來考查學生的知識熟練度.
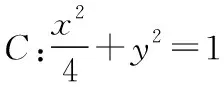
(1)略;
(2)在x軸上是否存在定點,使得直線TA與TB的斜率互為相反數?
【分析】(2)由題意可知,直線l的斜率存在且不為0,先假設存在定點并設為T(x0,0),用坐標直接表示出kTA,kTB,然后借助韋達定理就能求出滿足條件的x0.
【題目1(2)改編題1】(2)在y軸上是否存在與點P不同的定點Q,使得直線QA與QB的斜率互為相反數?若存在,求出點Q的坐標;若不存在,請說明理由.
題目1經過這樣改編,就成為一道直接考查兩直線斜率關系的基礎題.這種追根逐源,透過現象看本質的命題辦法,在命制試題時經常使用.
3.2 以角度關系為切入點來命制試題
直線的傾斜角與斜率有著密切的聯系,斜率問題向前走一步可以轉化為角的問題來呈現,進而考查學生的化歸與轉化能力.
3.2.1直接給出角度關系
【題目1(2)改編題2】(2)在軸上是否存在與點P不同的定點Q,使得∠PQA=∠PQB?若存在,求出點Q的坐標;若不存在,請說明理由.
3.2.2 用線段比值設置問題,暗含角度關系
如果兩個三角形相似,則對應角相等,對應線段成比例.因此,在命制試題時,可以以線段成比例為視角,通過恰當的化歸與轉化把問題轉化為對應角相等,在問題中經常以構建直角三角形實現轉化與溝通.
題目1第(2)問就是用線段比值的視角來命制的斜率問題.
3.2.3 借助面積比轉化為角度問題
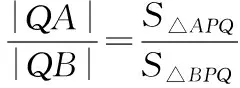
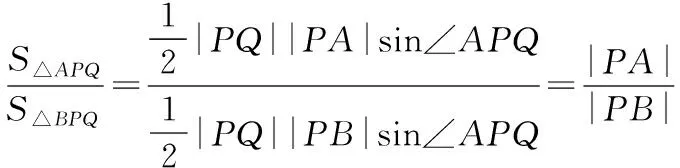
3.3 以直線過定點為切入點來命制試題
直線過定點可以轉化為定點與兩個動點連線的斜率相等,因此在命制試題時,可以用直線過定點來變相考查斜率問題.

(1)略;
(2)過點A(-4,0)的直線l與橢圓C1交于M,N兩點,點M關于x軸的對稱點為E.當直線l繞點A旋轉時,直線EN是否經過一定點?請判斷并證明你的結論.
【分析】(2)當直線l的斜率為0時,直線l與橢圓C1交于M,N兩點,則M,N兩點為橢圓C1的左、右頂點,因此點M關于x軸的對稱點E是點M本身,所以直線EN與x軸重合,由此可得直線EN若經過一定點,定點一定在x軸上,可設為T(x0,0).由題意可知,kTM=-kTE,然后根據kTE=kTN,結合韋達定理求出x0的值.
4.結束語
以考查橢圓的標準方程為落腳點命制試題時,圍繞a,b,c,e四個關鍵基本量如何建構兩個方程上下功夫,通過建構不同的方程來考查學生對基本知識和基本方法的掌握程度,不斷變換考查角度,靈活設置問題,考查學生的數學核心素養.命制此類試題可以從以下幾個方面思考如何設置問題,建立方程式:
①從考查橢圓定義的角度來命制試題;
②從考查橢圓性質的角度來命制試題;
③從考查點與橢圓的位置關系的角度來命制試題;
④從考查直線與橢圓的位置關系的角度來命制試題;
⑤從與其他曲線相結合的角度來命制試題.
以斜率為落腳點來命制考查直線與圓錐曲線位置關系命制試題時,可以直接考、間接考、變換考,把斜率、傾斜角、線段成比例和三角形面積等知識有機結合,不斷變化命題角度,靈活設置問題考查學生知識的遷移度和數學核心素養.


