海陸過渡相頁巖氣藏不穩(wěn)定滲流數(shù)學模型1)

陳志明 王佳楠 廖新維 曾聯(lián)波 趙鵬飛 Yu Wei

* (中國石油大學(北京)油氣資源與探測國家重點實驗室,北京 102249)

? (美國德州大學奧斯汀分校,美國奧斯汀 78712)

引言

海陸過渡相頁巖氣沉積環(huán)境穩(wěn)定,富有機質(zhì)頁巖大面積分布;發(fā)育微納米級孔?縫體系,具備較好儲集能力;富含石英等脆性礦物,有利于儲集層壓裂改造[1];頁巖地層壓力適中[2],含氣量高[3];存在大量微小孔洞和裂隙,但整體滲透率較差.為高效開發(fā)頁巖氣藏,壓裂技術(shù)的應用越來越廣泛[4-6].與普通氣藏相比,海陸過渡相頁巖常煤層、致密砂巖層互層,形成頁巖氣、煤層氣和致密砂巖氣疊置成藏[7],儲層連續(xù)性較差、橫向變化快、非均質(zhì)性強,水力壓裂技術(shù)是其獲得經(jīng)濟產(chǎn)量的關(guān)鍵手段[8].特別是海陸過渡相頁巖氣,地層可采性和可壓裂性良好,具有較好的穩(wěn)產(chǎn)能力,開發(fā)前景較好[9].然而,目前缺乏有效的海陸過渡相頁巖氣藏不穩(wěn)定滲流數(shù)學模型,對其滲流特征分析及儲層參數(shù)評價不利[10-12].因此,亟需開展海陸過渡相頁巖氣藏滲流模型的研究工作.

目前,國內(nèi)外一些學者在頁巖氣藏的滲流理論方面取得了良好的進展.1986年,Lee 和Brockenbrough[13]假設(shè)儲層和裂縫之間的流動方式是三線性流,建立了無限大均質(zhì)地層有限導流垂直裂縫井的三線性滲流模型.隨后,Ozkan 等[14]將三線性流解析模型應用于壓裂水平井試井分析中,分析了非常規(guī)儲層中的不穩(wěn)定滲流特征.進一步地,許多學者開展了頁巖氣藏的滲流理論工作[15-26].例如,高杰等[27]考慮了頁巖氣吸附解吸和擴散機理頁巖氣壓裂水平三線性流模型,通過數(shù)值反演求得考慮井儲和表皮系數(shù)的無因次井底壓力解,并繪制了壓力響應特征曲線,分析了頁巖氣藏不穩(wěn)定滲流特征.2016年,肖聰[28]針對頁巖氣藏中多級壓裂水平井和體積壓裂水平井裂縫網(wǎng)絡(luò)模型,綜合考慮吸附、擴散、基質(zhì)變形、天然裂縫應力敏感以及裂縫網(wǎng)絡(luò)高速非達西等非線性流動效應的作用,建立了考慮壓裂裂縫和天然裂縫耦合條件下的頁巖氣藏氣井滲流模型.2018年,任文希[29]采用離散裂縫模型對水力裂縫進行顯式處理,并采用連續(xù)介質(zhì)模型表征壓裂區(qū)和未壓裂區(qū),建立了考慮應力敏感、多組分滲流和多組分吸附的頁巖氣多級壓裂水平井滲流模型.2020年,Meng 等[12]基于滲流理論,建立了頁巖儲層復雜裂縫網(wǎng)絡(luò)系統(tǒng)條件下的滲流數(shù)學模型,模型中考慮了壓裂裂縫的非均勻性,并分析了頁巖儲層的不穩(wěn)定滲流特征.同年,吳明錄和丁明才[30]基于分形理論,考慮到天然裂縫的方向、位置、開度和長度等幾何規(guī)律,建立了分形離散裂縫網(wǎng)絡(luò)模型,并采用嵌入式離散裂縫和有限差分相結(jié)合的方法求解模型,得到了水平井井底壓力響應特征及影響規(guī)律,這些研究成果對頁巖氣藏滲流理論及特征研究具有十分重要作用.然而,由于海陸過渡相頁巖儲層的特殊物性[31],存在著滲透率極強非均質(zhì)性,其滲流數(shù)學模型未見報道,不利于海陸過渡相頁巖氣藏滲流特征分析及儲層參數(shù)評價.

針對這一問題,本文考慮頁巖氣吸附解吸,擴散,裂縫特點,以及海陸過渡相非均質(zhì)性等特征,建立并求解徑向非均質(zhì)頁巖氣藏壓裂直井的不穩(wěn)定滲流數(shù)學模型,得到典型的頁巖氣藏不穩(wěn)定滲流特征,建立海陸過渡相頁巖氣井的儲層參數(shù)評價方法,并進行數(shù)值模擬驗證,最后針對鄂爾多斯盆地海陸過渡相典型頁巖氣井開展了實例分析應用,可為同類頁巖氣藏的壓裂評價提供理論支撐.

1 海陸過渡相頁巖氣藏滲流數(shù)學模型

1.1 物理模型

海陸過渡相頁巖氣藏的物理模型如圖1 所示,考慮壓裂施工和儲層橫向變化快,物理模型考慮了壓裂裂縫和滲透率的非均質(zhì)性.頁巖氣藏為圓形封閉水平等厚,頂?shù)诪椴粷B透隔層;利用雙重介質(zhì)模型描述頁巖儲層天然裂縫和基質(zhì)系統(tǒng);考慮基質(zhì)系統(tǒng)的頁巖氣吸附解吸特性,利用Langmuir 等溫吸附曲線描述吸附氣體壓力與被吸附量的關(guān)系;經(jīng)過壓裂后,近井形成雙翼水力裂縫,水力裂縫為有限導流裂縫.根據(jù)上述物理模型,建立海陸過渡相頁巖氣藏壓裂直井數(shù)學模型.

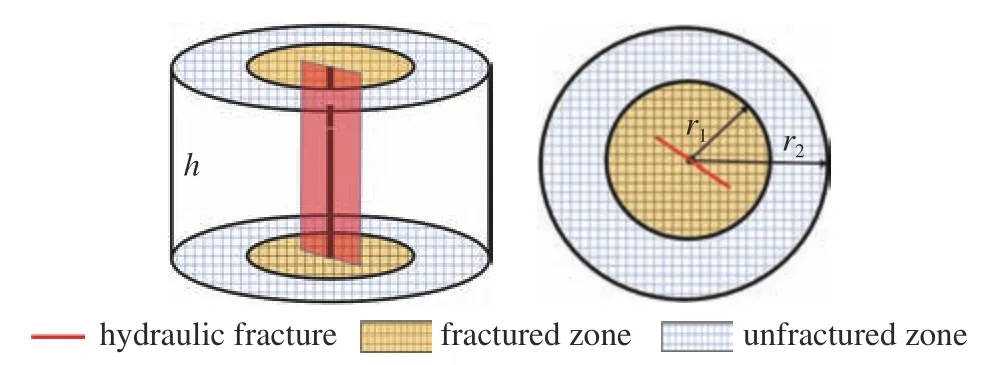
圖1 海陸過渡相頁巖氣壓裂直井模型Fig.1 Fractured vertical well model

1.2 數(shù)學模型

由于頁巖氣藏存在吸附解吸,Langmuir 方程為

其中,V為頁巖氣濃度,m3/kg;VL為吸附體積,m3/t;pL為解吸壓力,MPa.引入氣體擬壓力

(1)儲層滲流方程為

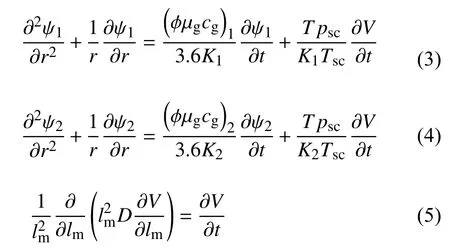
其中,1 表示內(nèi)區(qū);2 表示外區(qū);D為擴散系數(shù),m2/s;lm為基質(zhì)塊邊長,m.初始條件和內(nèi)外邊界條件為

式中,qsc為地面產(chǎn)量,m3/d;psc為地面壓力,MPa;Tsc為地面絕對溫度,K.

(2)壓裂裂縫滲流方程為

式中,WFKF為裂縫導流能力,mD·m;WF為裂縫寬度,m;KF為裂縫滲透率,mD.初始條件和內(nèi)外邊界條件為

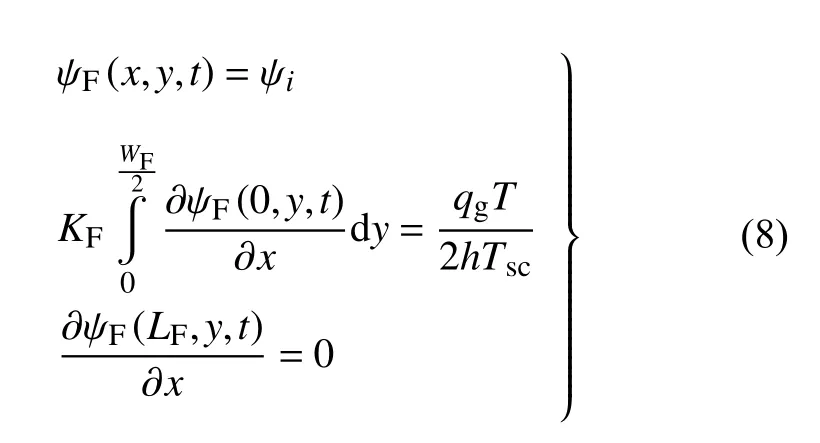
(3)無因次滲流數(shù)學方程為

為使方程簡潔,引入無量綱量如附錄A,可得無因次的儲層滲流數(shù)學模型

式中, ψ1,2D為內(nèi)外區(qū)儲層擬壓力,無因次.同時,可得無因次裂縫滲流數(shù)學模型

式中, ψFD和CFD分別為裂縫擬壓力和裂縫導流能力,無因次;qF為裂縫流量線密度,m3/(d·m);q為裂縫中的流量,m3/d;qFD為裂縫流量線密度,無因次.

1.3 模型求解

采用邊界元方法對非均質(zhì)油藏滲流模型進行求解.首先對油藏基質(zhì)滲流模型進行Laplace 變換,并利用微分算子進行簡化表示,同時考慮內(nèi)區(qū)裂縫井生產(chǎn)狀況,可得:

(1)油藏基質(zhì)滲流模型解

式中 δ 為Laplace 算子,無量綱.

同樣可得

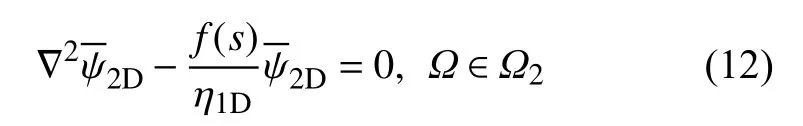
對于控制方程式 (11),引入Green 方程

很顯然,方程為無限大地層點源解,滿足

兩邊同乘ψ1D,則可將上述方程變形為

同樣對式 (11) 兩邊同乘G1得

將式 (15) 減去式(16) 并在區(qū)域1 內(nèi)積分

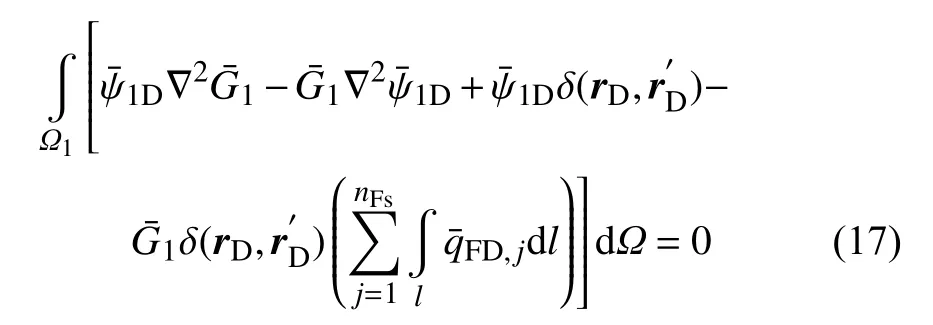
根據(jù) δ 函數(shù)和格林函數(shù)的性質(zhì)

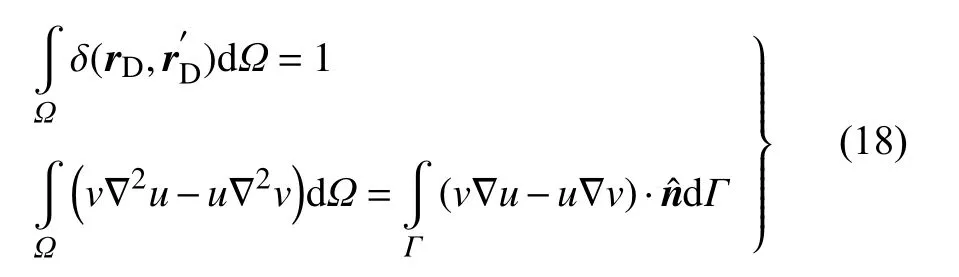
式(17)可得

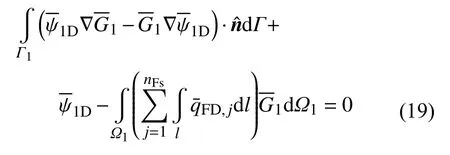
通過整理,可得區(qū)域1 無因次壓力解

同樣可得,區(qū)域2 無因次壓力解

(2)連接面條件

(3)壓裂裂縫滲流模型解

對壓裂裂縫滲流基本方程進行Laplace 變換得

利用積分方法可得

將邊界和裂縫單元進行離散,如圖2.假設(shè)邊界線 Γ1和 Γ2分別被劃分為N1和N2個邊界單元,裂縫被劃分為nFs裂縫單元和nFv裂縫點,如下圖所示.

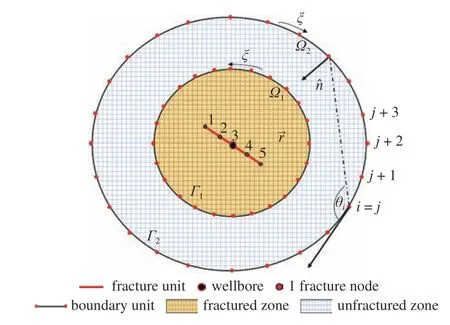
圖2 邊界離散示意圖Fig.2 Discretization of reservoir boundaries

根據(jù)離散邊界單元的幾何性質(zhì),式(19)～式(27)可離散為

①儲層滲流模型解

②連接面條件

③壓裂裂縫滲流模型解

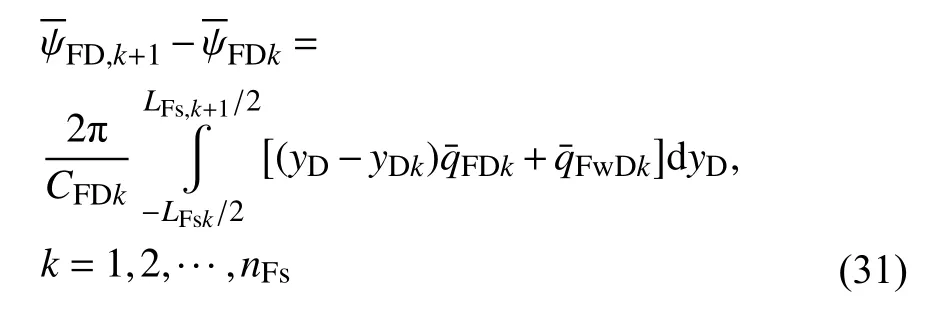
④輔助方程

利用質(zhì)量守恒方程來考慮裂縫節(jié)點處流動,同時考慮定產(chǎn)量生產(chǎn)條件,則可得

式(28)～式(32) 組成了一個 2nFv+nFs+4N1+N2階方程組.而對應的未知量為nFv個裂縫節(jié)點壓力pFD,nFv個裂縫節(jié)點出流量qwD,nFs個裂縫單元的單位長度流量qFD,N12個邊界單元節(jié)點壓力(ψ12,ψ21,ψ2) 和 2N1邊界單元壓力梯度 (?ψ12,?ψ21).可以看出,方程組是封閉的.對方程組進行聯(lián)立求解,即可得到每一個裂縫節(jié)點壓力ψFD(rD,s),包括井筒節(jié)點ψwD.考慮井筒儲集效應及表皮效應,進一步得到井底壓力響應為

式中,ψwCD為包含井儲效應和表皮效應的拉氏空間井底壓力解,無因次;CD為井筒儲集系數(shù),無因次;S為井筒表皮因子,無因次.最后運用stehfest 數(shù)值反演[31]即可得到實空間下的井底壓力解.

2 海陸過渡相頁巖氣藏不穩(wěn)定滲流特征

2.1 不穩(wěn)定滲流特征

基于時間與井底壓力和壓力導數(shù)的雙對數(shù)曲線特征,可分析海陸過渡相頁巖氣藏不穩(wěn)定滲流特征.根據(jù)上述數(shù)學模型解,取基礎(chǔ)參數(shù)如表1 所示,繪制頁巖氣藏壓裂井模型的時間與壓力和壓力導數(shù)的雙對數(shù)曲線,如圖3 所示.從圖可看出,海陸過渡相頁巖氣藏不穩(wěn)定滲流特征可分為以下階段:I 為流動早期階段:其受到井筒存儲效應及表皮效應的影響,在初期,壓力導數(shù)曲線表現(xiàn)為45°和隆起;II 為雙線性流階段:此階段流體從地層線性流入裂縫,裂縫流體線性流入生產(chǎn)井筒的階段,其壓力導數(shù)曲線的斜率為1/4;III 為線性流階段:此階段是流體從地層線性流入有限導流裂縫的流動階段,壓力導數(shù)曲線斜率為1/2;IV 為徑向流階段:壓力導數(shù)曲線的值等于0.5 的水平線,達到內(nèi)區(qū)徑向流階段;V 為頁巖氣解吸階段,頁巖氣的解吸發(fā)生在該階段,壓力導數(shù)出現(xiàn)下凹;VI 為內(nèi)外徑向流過渡,壓力導數(shù)上升;VII 為外區(qū)徑向流階段:壓力導數(shù)曲線的值等于0.5M 的水平線;VIII 為邊界控制階段,該階段主要受邊界條件影響,出現(xiàn)壓力導數(shù)曲線上揚的情況.

圖3 海陸過渡相頁巖氣藏不穩(wěn)定滲流特征Fig.3 Characteristics of unstable flow in marine-continental transitional shale gas reservoirs

表1 徑向復合氣藏壓裂直井模型參數(shù)取值表Table 1 Parameter table of fractured vertical well model in radial composite gas reservoir

2.2 不穩(wěn)定滲流特征

為了更好的認識海陸過渡相頁巖氣藏不穩(wěn)定滲流特征,了解不同的參數(shù)對其影響,運用控制變量法,研究一系列參數(shù)對滲流特征的敏感性影響,這些分析將為后續(xù)模型應用提供理論支撐.

2.2.1 裂縫半長的影響

根據(jù)不同的裂縫半長,分析對不穩(wěn)定滲流特征影響,如圖4.由圖可知裂縫半長主要影響雙線性流和線性流階段,隨著裂縫半長的增大,受影響的雙線性流階段結(jié)束時間推遲,其持續(xù)時間變長.同時,由于裂縫更靠近內(nèi)區(qū)邊界,使得壓力波更早到達內(nèi)區(qū)徑向流階段.

圖4 裂縫半長對不穩(wěn)定滲流特征的影響Fig.4 Influence of fracture half-length on unstable flow characteristics

2.2.2 裂縫導流能力的影響

根據(jù)不同裂縫的導流能力,分析對不穩(wěn)定滲流特征影響,如圖5.由圖可知裂縫導流能力主要影響中期流動階段,隨著裂縫導流能力增加,圖像整體下移,壓力降變小,壓力變化變緩,裂縫導流能力的變化對流動晚期影響較小.

圖5 裂縫導流能力對不穩(wěn)定滲流特征的影響Fig.5 Influence of fracture conductivity on unstable flow characteristics

2.2.3 解吸壓力的影響

根據(jù)不同解吸壓力,分析對不穩(wěn)定滲流特征影響,如圖6.由圖可知解吸壓力主要影響基質(zhì)系統(tǒng)流體向天然裂縫系統(tǒng)的供給階段.隨著臨界解吸壓力的增大,曲線整體下移,流體供給階段的開始時間滯后,同時下凹段越來越不明顯,直至逐漸消失.

圖6 臨界解吸壓力對不穩(wěn)定滲流特征的影響Fig.6 Influence of critical desorption pressure on unstable flow characteristics

3 模型驗證

利用數(shù)值模擬方法對數(shù)學模型進行驗證,建立一口海陸過渡相壓裂直井的數(shù)值模型(圖7).數(shù)值模型孔隙度為3.08%,目的層儲層溫度68 °C,原始地層壓力為 22 MPa,裂縫半長為30 m,裂縫導流能力100 mD·m,氣藏厚度5.4 m.壓裂直井進行壓降測試,流量為1000 m3/d,數(shù)值模擬測試數(shù)據(jù)見圖8.利用文中建立的數(shù)學模型與數(shù)值模型進行對比驗證,由模型驗證參數(shù)表(表2)和結(jié)果對比圖(圖8)可知,數(shù)學模型計算結(jié)果與數(shù)值模型結(jié)果基本一致.

圖7 海陸過渡相頁巖氣壓裂直井數(shù)值模型Fig.7 Virtual well model

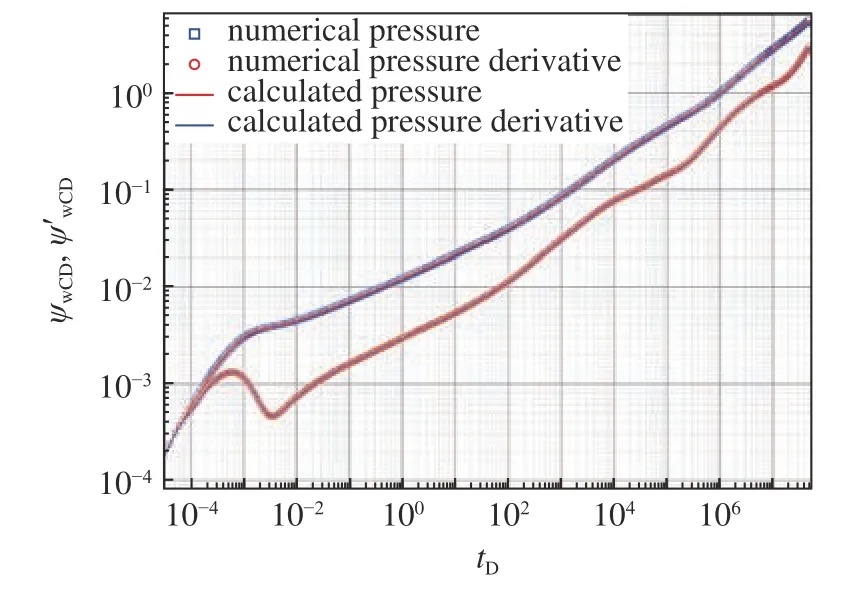
圖8 文中計算結(jié)果與數(shù)值模擬結(jié)果對比驗證Fig.8 Calculated results compared with the numerical simulation results

表2 模型驗證參數(shù)表Table 2 Model parameters

4 模型應用

基于海陸過渡相頁巖氣藏不穩(wěn)定滲流數(shù)學模型,通過與實際礦場壓力測試數(shù)據(jù)擬合分析[3],可評價儲層及裂縫參數(shù).DDJ 井為 2017年海陸過渡相頁巖氣藏完鉆的一口壓裂井.為評價DDJ 井的壓裂裂縫參數(shù),開展了不穩(wěn)定壓力測試,測試過程如圖9.連續(xù)測試階段約進行了 1150 h,測試階段測試了 600 h,測試時間相對比較長.

圖9 實際擬合壓力測試數(shù)據(jù)Fig.9 Practical fitted pressure data

針對測試過程不穩(wěn)定壓力數(shù)據(jù)進行分析(圖9),發(fā)現(xiàn)存在不穩(wěn)定流動特征的I,III,IV,V 和VI 階段.其中,第I 階段為流動早期階段,其受到井筒存儲系數(shù)以及表皮系數(shù)的影響;第II 階段沒有很明顯出現(xiàn),主要是因為裂縫半長較短導致流體在裂縫中的流動時間較短;第III 階段為線性流階段,流體從地層線性流入有限導流裂縫的流動階段;第IV 階段為徑向流階段,達到內(nèi)區(qū)徑向流階段;第V 階段為頁巖氣解吸階段,頁巖氣的解吸發(fā)生在該階段;第VI 階段為內(nèi)外徑向流過渡.利用建立的頁巖氣壓裂井滲流數(shù)學模型,對壓力測試數(shù)據(jù)開展擬合分析(圖9),擬合分析和裂縫參數(shù)評價結(jié)果如表3.分析發(fā)現(xiàn),經(jīng)過壓裂改造后,典型井附近形成了主裂縫和改造區(qū),主裂縫為有限導流兩翼縫,裂縫半長為31～33 m,導流能力為93～101 mD·m,改造區(qū)半徑為100 m,改造區(qū)滲透率為0.2～0.3 mD.典型井控制半徑約為318 m,控制可采儲量約為8.52 × 106m3.

表3 擬合分析參數(shù)結(jié)果表Table 3 Evaluated parameters using type-curve matching

5 結(jié)論

(1)考慮頁巖氣吸附解吸,擴散,裂縫特點,以及海陸過渡相非均質(zhì)性等特征,建立并求解徑向非均質(zhì)的頁巖氣藏壓裂直井不穩(wěn)定滲流數(shù)學模型,得到典型的頁巖氣壓裂井試井曲線特征,并進行了數(shù)值模擬驗證,最后針對鄂爾多斯盆地海陸過渡相典型頁巖氣井開展了實例分析應用,可為同類頁巖氣藏的壓裂評價提供一些理論支撐.

(2)海陸過渡相頁巖氣藏不穩(wěn)定滲流特征可分為以下階段:I 為流動早期階段:其受到井筒存儲效應以及表皮效應的影響,在初期,壓力導數(shù)曲線表現(xiàn)為45°;II 為雙線性流階段:此階段流體從地層線性流入裂縫,裂縫流體線性流入生產(chǎn)井筒的階段,其壓力導數(shù)曲線的斜率為1/4;III 為線性流階段:此階段是流體從地層線性流入有限導流裂縫的流動階段,壓力導數(shù)曲線斜率為1/2;IV 為徑向流階段:壓力導數(shù)曲線的值等于0.5 的水平線,達到內(nèi)區(qū)徑向流階段;V 為頁巖氣解吸階段,頁巖氣的解吸發(fā)生在該階段,壓力導數(shù)出現(xiàn)下凹;VI 為內(nèi)外徑向流過渡,壓力導數(shù)上升;VII 為外區(qū)徑向流,壓力導數(shù)曲線的值等于0.5M 的水平線;VIII 為邊界控制階段,該階段主要受邊界條件影響,出現(xiàn)壓力導數(shù)曲線上揚.

附錄

無量綱量

引入儲層滲流方程無量綱量如下

其中 ,ω為彈性儲容比,無量綱.

同時,引入關(guān)于裂縫無因次量如下

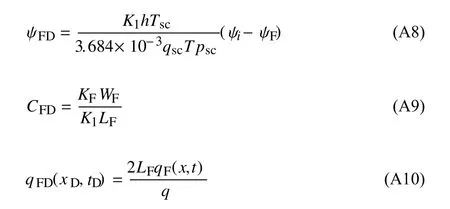
式中,ψFD 和CFD分別為裂縫擬壓力和裂縫導流能力,無因次;qF為裂縫流量線密度,m3/(d·m);q為裂縫中的流量,m3/d;q FD為裂縫流量線密度,無因次.