一道競賽題的探究
2021-11-10 06:19:58重慶三峽學院數學與統計學院404000古玲玲陳曉春
中學數學研究(江西) 2021年10期
重慶三峽學院數學與統計學院 (404000) 羅 建 古玲玲 陳曉春
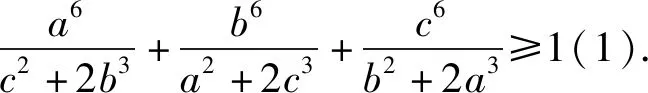
本文擬對不等式(1)的證明方法、變式、推廣等方面作一探究.
1.不等式(1)的證法探究
分析1:不等式(1)的左端結構對稱,利用柯西不等式有:
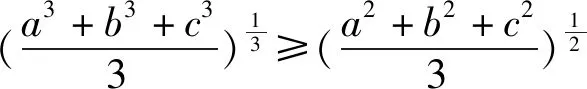
分析2:若注意到不等式(1)的左端的結構,利用基本不等式證明局部不等式后再疊加則有:
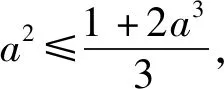
分析3:前述兩種證法的關鍵是尋求a2+b2+c2與a3+b3+c3的不等關系,除證明1及證明2 外,還有

2.不等式(1)的變式
從證明1的過程可知,在使用柯西不等式后只要分母的和a2+b2+c2+2(a3+b3+c3)以及分子的和a3+b3+c3不變,其證明方法都是相同的,因此可得如下(1)的變式不等式:
2.1 將分子的元素輪換
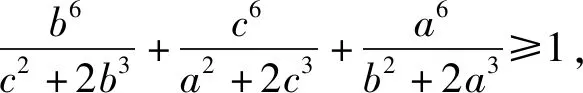
2.2 將分母的元素重排
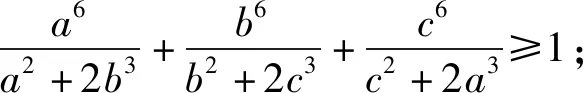
2.3 將分母的元素拆分并輪換
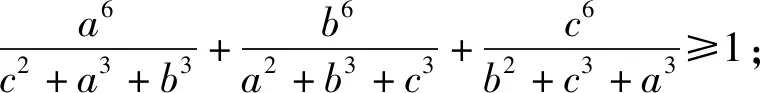
2.4 將分母的多項式擴充

顯然,通過對不等式中相應項的變式有很多,因此不等式(1)的變式還有許多,有興趣的不妨一試.
3.不等式(1)的推廣
推廣是數學探究中的一種常用的思維形式,將不等式(1)的系數一般化,元素個數推廣有:
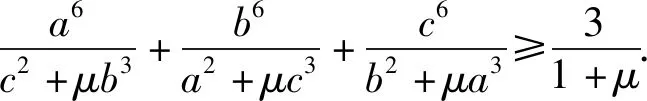
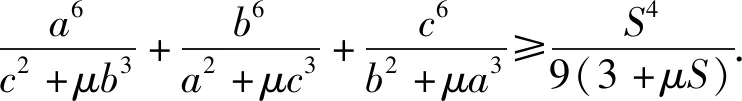
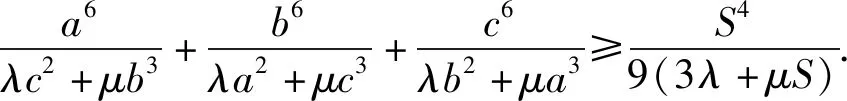
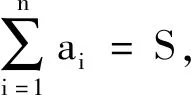
不等式5-8,前一個均是后一個的特例,下面只給出不等式8的證明.
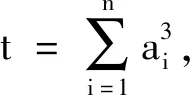
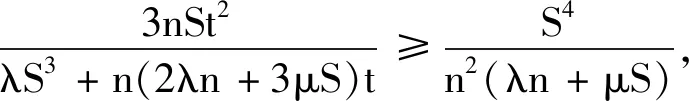
猜你喜歡
中學生數理化·七年級數學人教版(2022年5期)2022-06-05 07:51:48
中等數學(2021年11期)2021-02-12 05:11:46
民用飛機設計與研究(2020年4期)2021-01-21 09:15:02
電子制作(2018年18期)2018-11-14 01:48:24
快樂語文(2018年13期)2018-06-11 01:18:16
中等數學(2018年11期)2018-02-16 07:47:42
山東工業技術(2016年15期)2016-12-01 05:31:22
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
中學生數理化·高二版(2008年7期)2008-06-15 01:31:20

