探析2020年全國高中數學聯賽浙江初賽導數題
浙江省衢州第二中學 (324000) 廖如舟
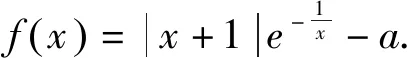
(Ⅰ)若f(x)=0恰有三個根,求實數a的取值范圍;
(Ⅱ)在(Ⅰ)的情形下,設f(x)=0的三個根為x1,x2,x3,且x1 本題以絕對值函數和指數函數為載體,主要考查函數導數、不等式、絕對值等基礎知識,其核心是通過導數分析函數的單調性,結合局部判斷等手段得到函數的大致圖像.浙江省初賽導數題設計的特點是規避題海、綜合性強、注重區分.第(Ⅱ)小題判斷方程的根之間的不等關系,考查學生推理論證、分類討論、轉化化歸等分析解決問題的能力.促進學生邏輯推理、數學建模、數學運算、直觀想象、數據分析等數學核心素養的培養. 命題組給出了如下的參考答案: 圖1 圖2 從命題組提供的解答中能夠感受到命題者對于題目設計的精巧之處,追本溯源可以發現在《數學分析中的典型問題與方法》一書中有一題與本題函數模型類似: 圖3 圖4 可以肯定的是很少會有學生按照參考答案的思路解題,而是會采用分析法利用函數單調性證明不等式,思路清晰,過程簡單,筆者在考后的第一時間完成本題,用的是如下解法: 通過分析證明的過程發現只用到了一個不等式ex≤x-1.從這個角度出發再改進一下本題證明: 導數是用來研究函數局部性質的一種重要的工具,是微積分中重要的基礎概念,其核心是用導數來研究連續函數的單調性,主要培養學生邏輯推理、數學建模、數學運算、直觀想象、數據分析等數學核心素養. 從知識點看,本題涉及的內容大都是學生熟悉的知識點,大部分學生做不出本題的原因有:(1)題目的新穎,比較少見的導數處理絕對值的問題,且還是絕對值函數和指數型函數的乘積形式;(2)容易與極值點偏移聯系在一起,在處理多變量不等式轉化的時候,運算分析能力不夠,同時沒有在合適的地方使用切線不等式放縮;(3)缺乏對解決問題的路徑進行規劃和試題命制背景的探究,缺少對于尋找同性態函數的勇氣,存在著循規蹈矩的思想,大部分學生不敢想、不會想,這個是當前教學亟待解決的問題. 基于以上分析,從發展學生核心素養角度審視導數教學,我們認為要培養學生三個方面的能力[1]. 第一,培養“敢想”的能力.在教學中,注重知識的發生、發展過程,引領學生認識導數的整體結構、本質,夯實基礎知識,選擇一些典型或者新穎的導數題進行教學,幫助學生建立方法體系,如學會用導數去分析函數的性質,進而刻畫函數的圖象,注意函數變化過程的增幅和趨勢,通過一題多解,比較各種解法的優劣,培養學生的數學理性思維,發展學生數學直觀想象、邏輯推理素養. 第二,指導“強算”的能力.為了突破導數問題的“運算關”,在導數教學中,選擇一些優秀的解法的推理演算過程,通過剖析展示運算錯誤的原因,指導學生明晰運算對象的基礎上,采用估算、口算、整體運算等方法,預判運算實施的可能性,養成在腦中建立思維過程的習慣,提升運算素養. 第三,引導“鉆研”的能力.在導數的教學中,常常要考慮從命題者的角度去剖析思考問題,培養學生對問題的分析態度,養成探究的習慣,對于課堂的問題加以延伸和推廣,實現有意義的深度學習.1 試題分析
2 解法探究
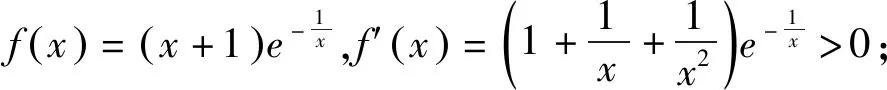

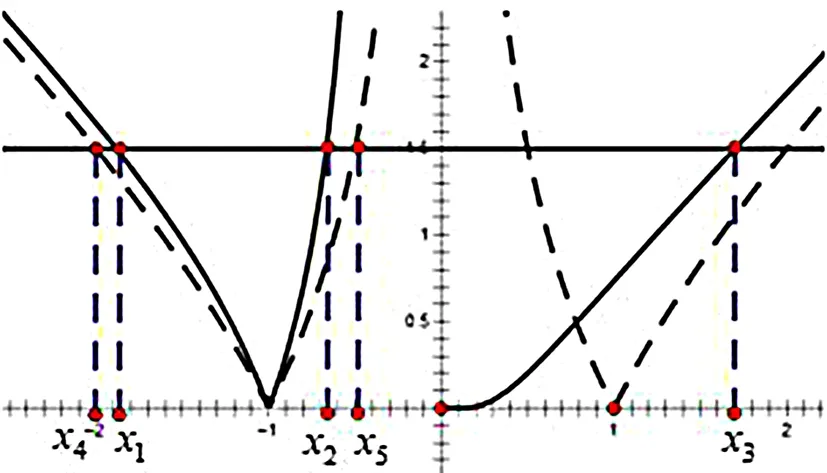

3 命制源流
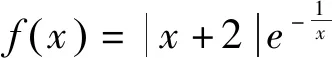
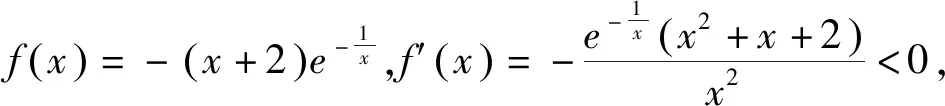


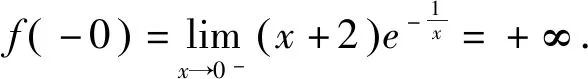
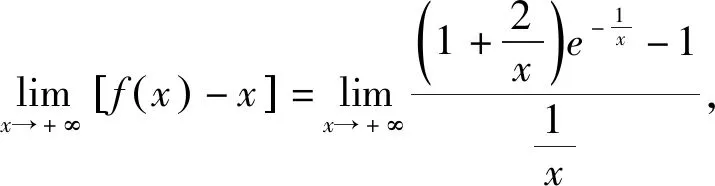




4 拓展延伸
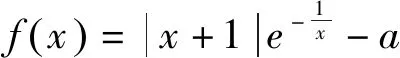
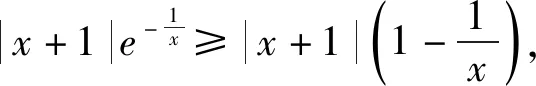
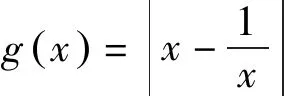
5 教學啟示

