沖擊載荷下顆粒材料臨邊界區域的波動行為及變形特征分析1)

王 蕉 楚錫華

* (西南交通大學力學與工程學院,成都 611756)

? (武漢大學土木建筑工程學院,武漢 430072)

引言

作為離散顆粒材料的土壤(或巖體),是日常生活中最常見的隨機多孔介質,沖擊載荷作用下材料的動力學響應對于工程實踐和地質災害防控有著重要的指導意義.注意到應力波的傳播行為與介質性質密切相關,基于應力波的行為特征分析可提供一種非侵入式研究顆粒材料性質的途徑.因此有非常多的學者致力于研究沖擊載荷作用下顆粒材料的動力學響應.

在過去幾十年中,一維顆粒鏈中的波傳播行為一直是一個備受關注的話題[1-3].在研究過程中,研究人員通常在邊界處設置傳感器,從多方面研究顆粒材料中的波特性[4],但很少討論邊界區的情況[5-6].對于更復雜的塑性接觸問題,研究者們構建了具有彈性和塑性特性的理想顆粒材料模型,研究不同的載荷條件下單分散的彈性和彈塑性顆粒鏈的動力學響應,給出了波傳播過程中能量衰減的機制[7-9].Hayden 等[10]開發了彈塑性球體動態壓縮力?位移模型來研究由金屬球體組成的系統對撞擊的響應,模擬中使用大型周期性顆粒晶體,以確定材料中應力波速的控制因素.除了天然材料之外,基于顆粒物質的超材料設計一直是一個充滿活力的研究領域,它結合了材料科學,非線性動力學和凝聚態物理等學科的思想[11].迄今為止大多數研究都集中討論一維晶體中的現象,基本回避了邊界問題[12].

對于二維、三維的情況,研究人員利用不同的方法研究了波在顆粒材料中的傳播行為[13-14],修晨曦和楚錫華[15]基于微形態模型研究了顆粒材料中波的頻散特性.Mouraille 等[16]利用周期性邊界條件,探討了應力波在顆粒材料中的傳播機制,分析了波速和頻散關系,并與基于宏細觀轉化的理論結果進行了對比.Awasthi 等[17]采用數值方法研究了材料中壓縮波的各向異性和傳播速度的影響.Chotiros和Isakson[18]發現在顆粒介質中的剪切波傳播會涉及與晶粒旋轉相關的能量.Huang 等[19]基于球形粒子模型,計算了砂土中剪切波速度的計算公式,其計算結果與現場測量數據非常吻合.Yang 和Sutton[20]通過數值和實驗方法研究了非線性波在密排顆粒通道中的傳播,證明了顆粒旋轉動力學的重要性.Lisyansky 等[21]研究了主脈沖在未壓縮的二維密排顆粒晶體中的傳播,通過降階模型描述了強定位主脈沖的空間演化.Keki 和Van Gorder[22]對具有赫茲相互作用勢的一維顆粒晶體中的孤波進行了研究,在界面兩側設置不同的相互作用勢,孤立波顯示出不同的反射和透射特性,并根據準粒子碰撞解釋了界面處的波傳播效應.Hua 和Van Gorder[23]研究了在赫茲接觸定律下二維球形晶體中的波傳播,討論了邊界處的波反射,盡管邊界的反復反射將使系統長時間陷入混亂狀態,但有許多有趣的波結構和模式會以瞬態的形式出現.除了對界面處波反射問題的簡單研究之外,Li 等[24]研究了波之間的相互作用,得到了波前速度和力幅值之間的通用關系.

顆粒材料中波傳播特性的一個重要研究目標是材料定制(即超材料設計),如何設計出具有特定導波特性的人工材料一直是研究者們努力的方向.Leonard 等[25]采用微型三軸加速度計來確定面內外碰撞所產生的應力波特性,研究了未壓縮不銹鋼球的二維方形堆積的動力響應.Leonard 等[26]還通過選取不同的材料組合,對應力波傳播過程中的波前形狀進行了調節.他們還通過試驗和數值模擬的方法,研究了顆粒質量和剛度比的系統變化對應力波波前形狀的改變.在這些顆粒系統中控制應力波前特性的能力可以用來研發新的波定制材料[27].這些結果為設計有效的減震結構開辟了道路,并為顆粒物質中波傳播的機理提供了新的見識[28].Xu 和Zheng[29]基于正方形密堆積和六角密堆積研究了二維布基球(buckyball C60)晶格的應力波行為,其計算結果與分子動力學模擬的結果非常吻合.Galich等[30]分析了彈性波在層狀介質中的傳播,分析了不同頻率范圍內帶隙的具體情況.Zhou 等[31]從基本波動方程出發,得出了二維固體聲子晶體帶隙的影響因素,并分析了波速比,聲阻抗比以及泊松比對帶隙的影響.

以上諸多研究工作主要從兩方面著手研究顆粒材料中的波傳播行為:(1)通過建立更精準的接觸本構模型(如彈塑性接觸模型),使計算所得的結果更符合實際.(2)通過人工設計顆粒材料內部結構,主動控制波在材料中的傳播行為.事實上在波傳播過程中,由于邊界的存在,邊界處應力波的反射、吸收等都把問題復雜化,目前的研究工作中只有極少一部分考慮了材料邊界對波傳播的影響;對邊界附近區域的設計也是超材料設計中極為重要的一部分,它往往比材料內部設計更有挑戰性.本研究從一維顆粒鏈中的波傳播出發,根據邊界的影響范圍,給出了臨邊界區域的定義;然后對不同顆粒排列方式下,不同形狀的臨邊界區域中波的傳播行為和顆粒材料的變形特征進行了分析.

1 臨邊界區域的定義

一維顆粒鏈模型由101 個半徑為0.5 mm 的顆粒組成,最右端設置剛性墻面,計算過程中時間步長dt設為0.01 μs,運動阻尼設為0.05.計算中使用了兩種常用的接觸本構模型,即線性接觸模型和赫茲接觸模型,接觸摩擦系數μ和接觸阻尼系數βn均為0.5.其他參數如法/切向接觸剛度,剪切模量以及泊松比等見表1.

表1 計算參數Table 1 Parameters used in the simulation

在模型最左端施加沖擊載荷,指定ID 為1 的顆粒有沿x方向的初速v0=1.0 m/s,分別記錄沿著初速度方向的若干觀測點處,波傳播過程中顆粒的速度,波速采用平均速度的定義,即波傳播距離l時,耗時為t,則平均波速v=l/t,如圖1、圖2 所示.在靠近邊界的局部區域,除正常沿程衰減(摩擦)的部分動能之外,顆粒能夠得到的最大動能(速度)明顯小于其他區域,顆粒的運動狀態與遠離邊界處有明顯不同,圖2 中也表現出同樣的速度變化規律.因此將距離邊界10 倍顆粒尺度的區域定義為臨邊界區域,以下分析主要限定在該區域中進行.

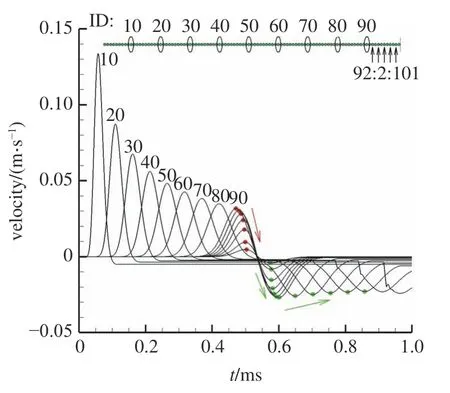
圖1 顆粒速度隨加載時間的變化(線性接觸模型)Fig.1 Particle velocity variation with loading time (linear contact model)

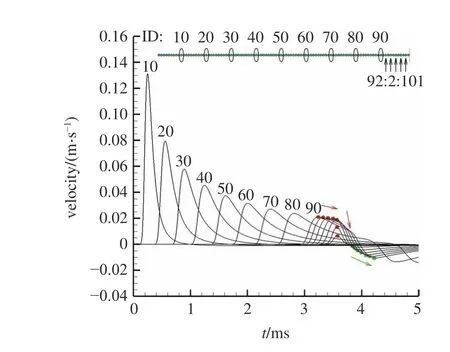
圖2 顆粒速度隨加載時間的變化(赫茲接觸模型)Fig.2 Particle velocity variation with loading time (Hertz contact model)

2 不同形狀邊界處波的反射

為探究邊界處波的反射,按照邊界墻體形狀的不同,分為以下3 類,如圖3 所示.

對于A,B 類θ范圍從0 每隔15°變化到75°,對于C 類θ范圍從0 每隔5°變化到45°.此外,變換顆粒排列方式,即單粒徑密排,單粒徑(r)隨機排列,均勻粒徑(rlo?rhi)隨機排列,如圖3(a)所示.在涉及顆粒材料中波傳播的研究當中,相比線性接觸模型,非線性的Hertz 接觸模型能更好地反映波在顆粒材料內的傳播特性.因此在下面的研究中,顆粒之間的接觸本構均采用Hertz 接觸,分別設置不同形狀的邊界,邊界與顆粒之間接觸力的計算也采用Hertz 模型,得到多組樣本,相關尺寸參數見表2,具體計算參數同表1.

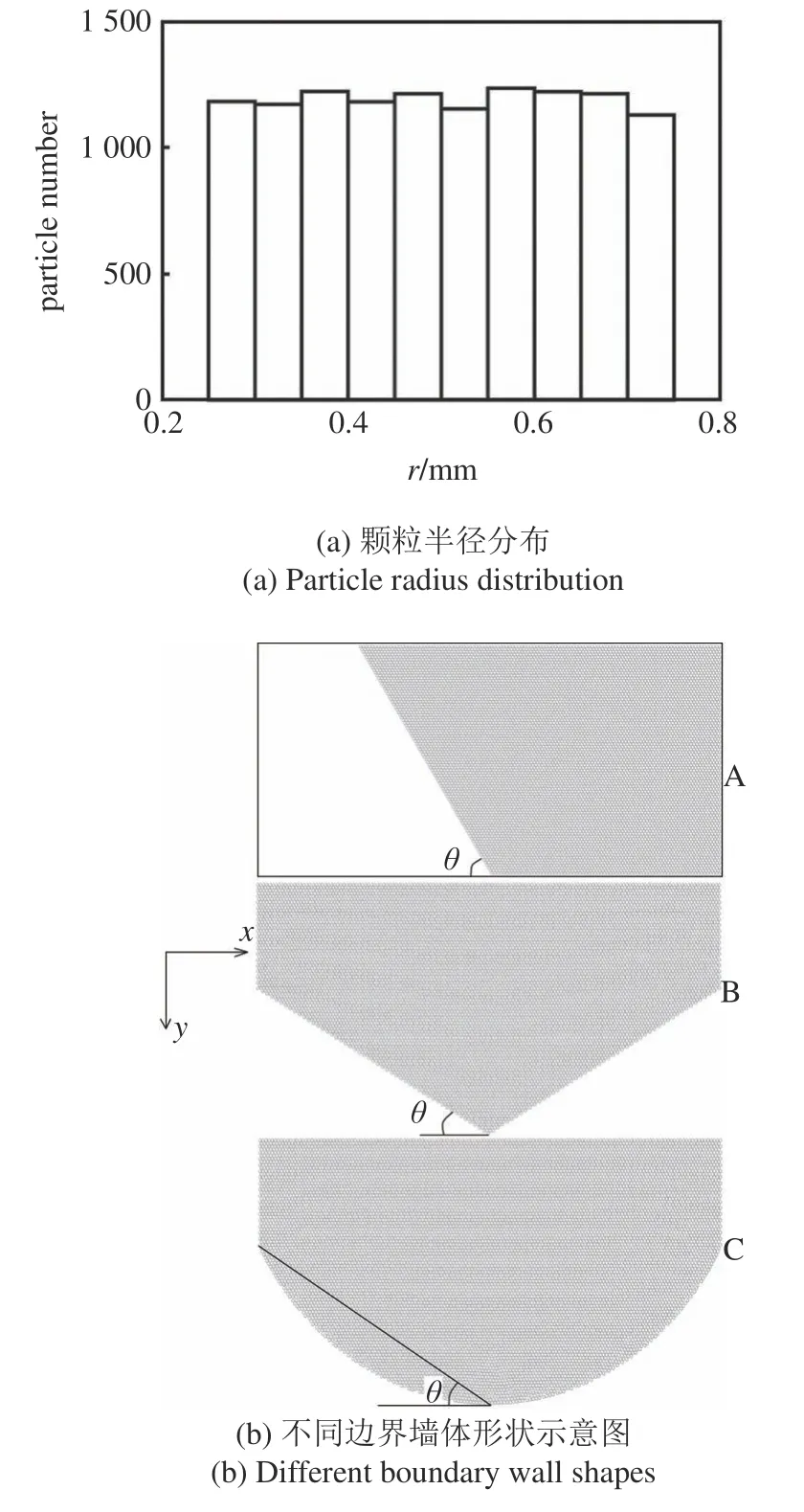
圖3 計算模型Fig.3 Simulation model

表2 二維樣本尺寸參數Table 2 Size parameters for 2-D specimen

對A 類密排顆粒樣本,以θ=0 和θ=60°為例,圖4 顯示了不同時刻應力波在樣本中的傳播情況.

由圖4 可以看出,波傳播初期,在主波形之后的次級波表現出了明顯的方向性圖4(b)～ 圖4(f),不同方向上傳播速度的差異.圖4(c)中明顯可以看到在距離激勵源相同遠近的下邊界和右邊界處,波前到達邊界的時間有較大差異,沿y方向的速度明顯更快.將圖4(c)單獨畫出,見圖5.根據圖中所示可以估算出橫向速度與縱向速度之間的比約為vx/vy=0.93,從豎向變化到橫向,隨著速度方向與x軸正向夾角變小,波傳播速度變小.

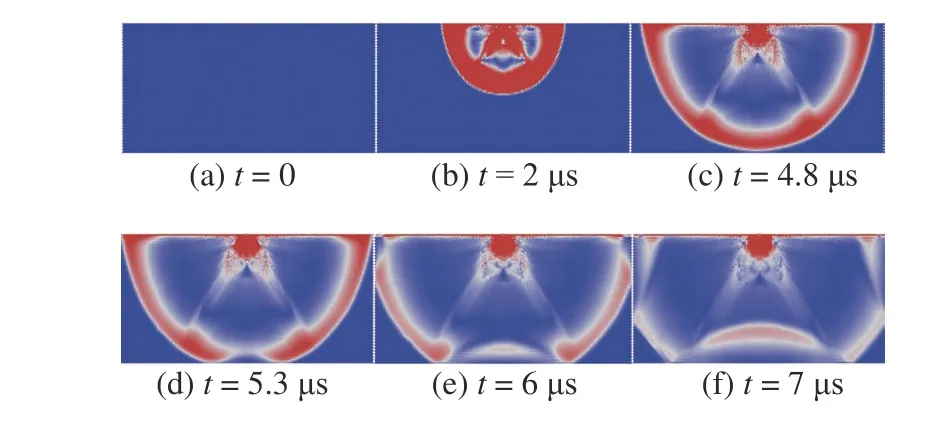
圖4 波前形狀隨時間演化θ=0Fig.4 Wavefront shape evolves over time (θ=0)

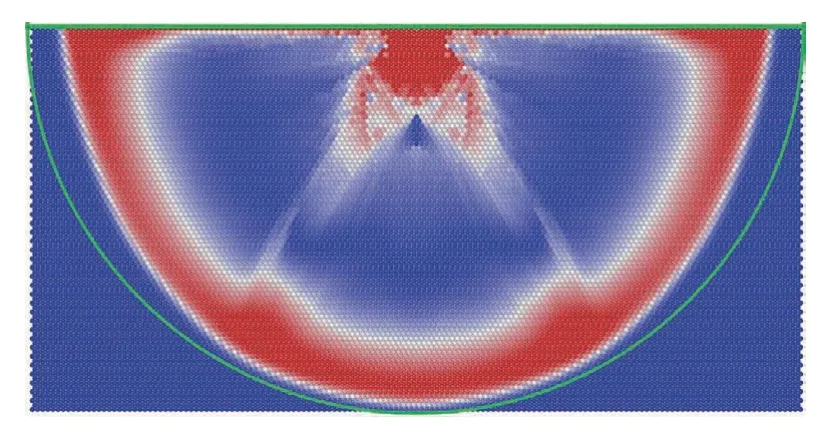
圖5 波前形狀分析示意圖Fig.5 Schematic diagram of wavefront shape analysis

根據之前的研究工作[32],在單一粒徑密排顆粒樣本中,波前形狀隨時間演化可以用以下式子來描述

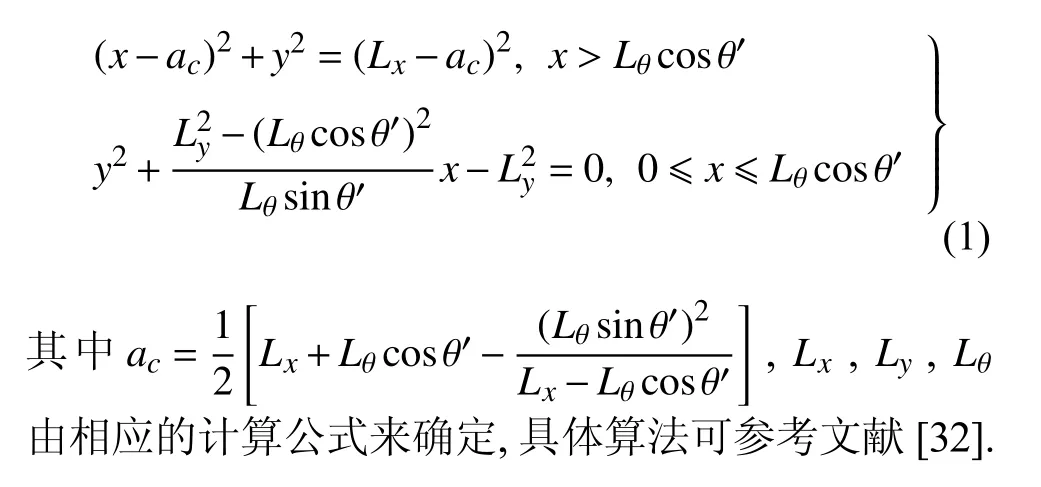
在之前的研究中沒有考慮邊界處的反射效應,此處將邊界的影響納入其中.圖6 顯示了邊界處反射之后波傳播的情況,圖中黑色虛線是無限大體中的波前形狀按下邊界進行鏡面對稱而得,黃色虛線是按左右邊界進行鏡面對稱而得;紅色長點劃線表示經下邊界反射后實際的波前形狀,黑色實線表示經左右邊界反射后實際的波前形狀.由圖可知下邊界與左右邊界處的反射有明顯的不同.為便于分析,仍然假設反射之后實際的波前形狀(紅色長點劃線)近似為圓弧,從圖中可以看出反射后的圓弧半徑明顯小于未經邊界反射的圓弧半徑.通過對波在時空中的演化過程進行細致分析,可以得出結論:下邊界處的反射會使波前形狀(圓弧)的半徑逐漸變小,這反映出反射后速度在不同方向上的分布呈現出中間高兩邊低的規律.左右兩邊反射后的波前形狀基本上為直線(黑色實線),即半徑為無窮大.這與下邊界的規律不一致,導致這種差異的主要原因是邊界處顆粒的排列方式不同.

圖6 邊界處應力波的反射Fig.6 Reflection of stress wave at the boundary

假設顆粒在邊界處的速度反射如圖7 所示,與邊界平行的速度分量不發生改變,與邊界垂直的速度分量反向.分別觀察下邊界和右邊界的細部圖可以看到,下邊界處顆粒與墻體接觸“緊密”,局部孔隙率(考慮邊界兩層顆粒)為0.137 6.右邊界處顆粒與墻體接觸“松散”,局部孔隙率為0.319 8.盡管顆粒的排列方式仍然規則,但經邊界反射之后,速度在樣本中的重分配會在孔隙處出現弱化(相同速度碰撞邊界的條件下,黃色顆粒獲得的動能將小于下邊界處綠色顆粒的動能),這在宏觀上表現為圖6 中黃色虛線向內收縮逐漸轉化為黑色直線的現象.

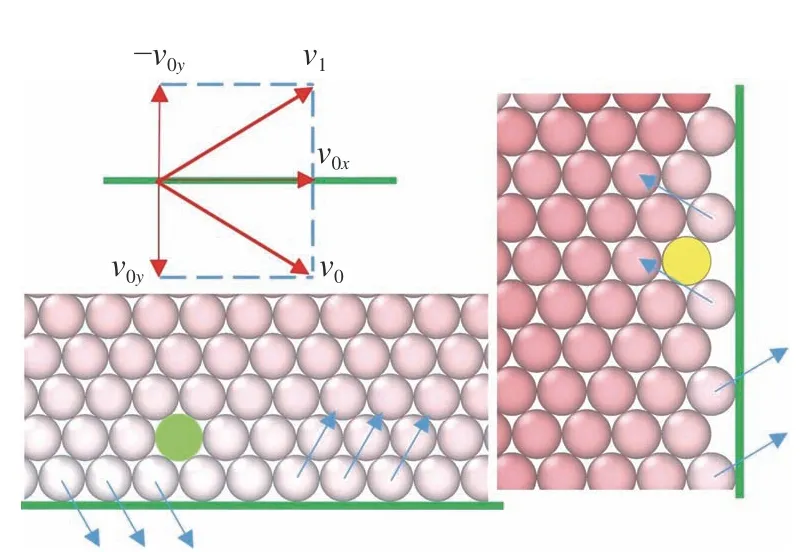
圖7 邊界反射細部圖Fig.7 Details of boundary reflection

對于θ=60°的A 類樣本,波前隨時間演化如圖8所示,應力波在邊界處的反射效果雖然不明顯,但仍然能看到反射后的波在樣本中的傳播情況,圖中標示了波前在樣本中的大致位置.除了能觀測到主波在邊界處反射之外,在圖8(e)中還能觀察到次級波在邊界處的反射(綠色波形),這個反射點與主波最初的反射點8(b)位置一致.

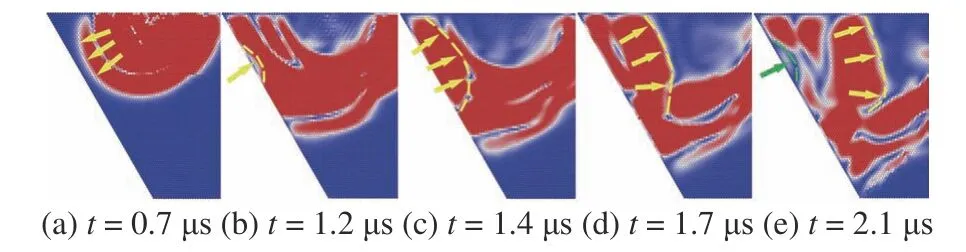
圖8 波前形狀隨時間演化θ=60°Fig.8 Wavefront shape evolves over time (θ=60°)

由于此時墻體角度與顆粒排列取向一致,可以得到形如圖9(c) 的規整邊界,圖中還展示了θ=30°和θ=45°時邊界細部情況,可以看到由于在靠近邊界處顆粒排列方式的細微差異,導致波在邊界處的反射表現出不同的形式.與θ=0 的情況相比,圖8(b)和圖10(a)經邊界反射后的波前形狀不明顯;對于局部孔隙率更大的θ=45°邊界圖9(b),甚至很難直接在臨邊界區內觀察到主波的反射現象.這是由于大孔隙的存在使臨邊界區內的顆粒有更多的“活動空間”,使顆粒攜帶的動能更容易分散到臨邊界區域中去,能量更易彌散開,而不是像圖6 所示的那樣朝著某個特定的方向傳播.

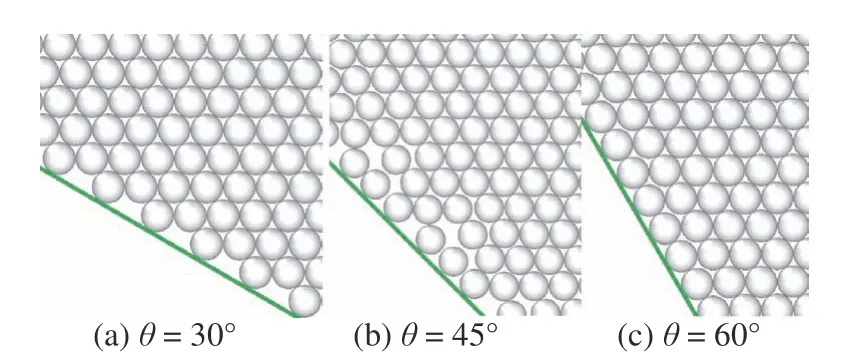
圖9 邊界細部圖Fig.9 Details of boundary

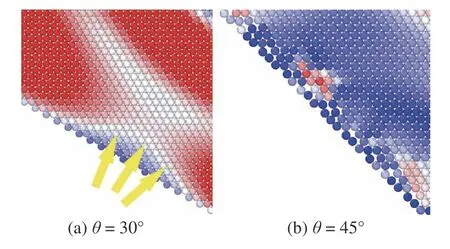
圖10 邊界反射圖Fig.10 Reflection at the boundary

為了驗證上面所得的結論,將樣本排列方式替換為單粒徑隨機排列和均勻分布多粒徑隨機排列,其他參數保持不變,這里仍然以θ=0°為例進行說明.如圖11 所示,當樣本受到沖擊載荷作用,波前形狀在到達邊界之前,基本保持為圓弧形,這反映出隨機排列樣本的各向同性性質.當主波到達邊界后,由于臨邊界區域內孔隙率較大,主波動能在臨邊界區發生了彌散,從而導致反射后的波前形狀很難直接觀察到.

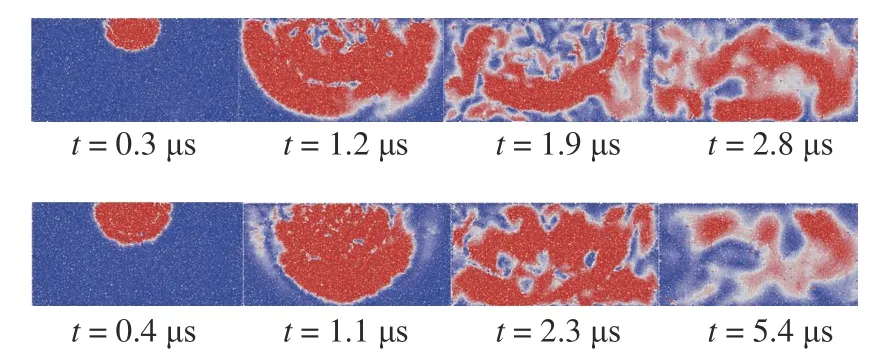
圖11 隨機排列樣本中波前演化圖.上:單粒徑,下:均勻分布多粒徑Fig.11 Wavefront evolution in randomly arranged specimens.Top:single-size particles,bottom:uniform distribution of multi-size particles

對于圖3 中B 類對稱邊界,由于密排顆粒取向的特殊性,在邊界與x軸夾角為0° (圖6),30°,60°時波前形狀隨時間的演化如圖12 所示.對于其他夾角的情況則幾乎很難直接觀察到波前在邊界處的反射,這是由于在臨邊界區域內部,孔隙率較大,顆粒動能發生彌散,這一現象還可以通過圖12 上左2 以及下左2 觀察到,當主波動能擴散到邊界時并沒有立刻發生反射,視覺上好像能量被臨邊界區域吸收了一樣,這部分能量將和后續次級波所攜帶的能量一起發生反射.隨著次級波的不斷傳播,原先主波攜帶的能量已經遠離邊界,次級波在邊界處發生反射,如圖12 下右2 所示.

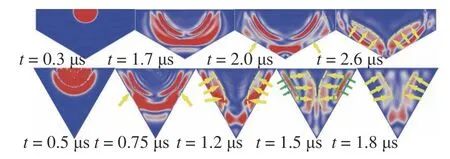
圖12 波前形狀隨時間演化.上:θ=30°,下:θ=60°Fig.12 Wavefront shape evolves over time.Top:θ=30°,bottom:θ=60°

對于反射波形的分析可以分為兩部分,在臨邊界區域內,反射波形主要受顆粒間的相互作用(方向)影響,表現為與顆粒排布方向一致的現象,如圖13所示:在臨邊界區反射波的波前形狀基本呈直線,并且與水平方向夾角約為順時針60°;在臨邊界區外(即材料中心區域),反射波形主要受應力波傳播速度的影響,波形會隨著時間不斷發生變化,在圖13 所示的時刻,可以看到中心區域的波形近似為兩段直線,第一段與水平方向夾角約為逆時針60°,第二段與邊界平行.對于折線邊界的情況,研究發現當θ>30° (如θ=60°,圖12 下左2)時,應力波從邊界一點處開始反射,反射波離開臨邊界區域時逐漸不與邊界平行,隨著角度增大,這種現象表現更加明顯.

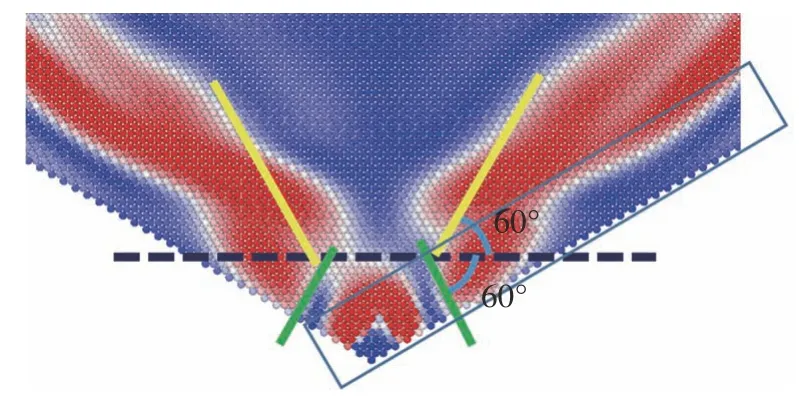
圖13 B 類邊界θ=30°波前形狀分析示意圖Fig.13 Schematic diagram of wavefront shape analysis of type B boundary θ=30°

對于圖3 中C 類對稱邊界,密排顆粒樣本很難保證臨邊界區域中較高的孔隙率,因此能直接觀察到的波反射現象并不明顯.與光或者聲音的反射進行類比,圓弧邊界應當具有匯聚效應,匯聚效應的強弱由圓弧邊界的半徑大小決定.臨邊界區域顆粒排列相對松散,這將使應力波反射的匯聚效應弱化.這兩個因素(邊界形狀和臨邊界區顆粒排列方式)共同影響應力波經材料邊界反射后的波前形狀.兩個因素是競爭關系,當圓弧半徑較大時,臨邊界區顆粒排列方式占據主導地位,臨邊界區域反射現象不明顯;隨著圓弧半徑減小,邊界形狀的影響逐漸增強,經材料邊界反射后的波向圓心附近匯聚,如圖14 下右1所示.

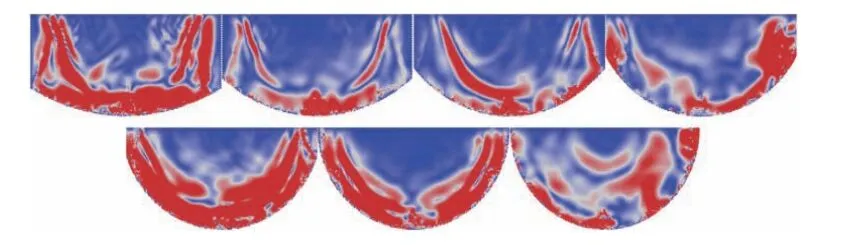
圖14 C 類邊界樣本中應力波的反射Fig.14 Reflection of stress wave at type C boundary

分別將樣本排列方式替換為單粒徑隨機排列和均勻分布多粒徑隨機排列,其他參數保持不變,經邊界反射之后波在樣本中的傳播如圖15 和圖16 所示,觀察到的現象與前面所得的結論一致.

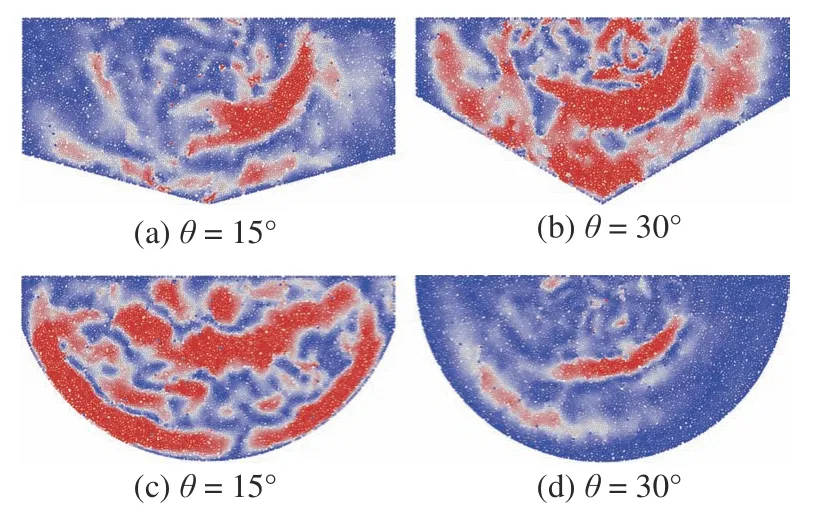
圖15 單粒徑隨機排列樣本波前形狀圖Fig.15 Wavefront shape in randomly arranged samples of single-size particles

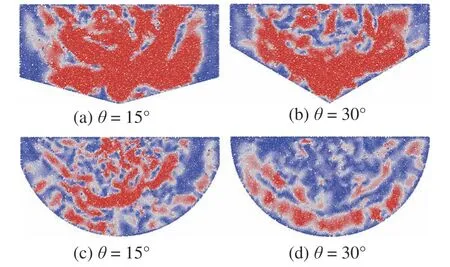
圖16 均勻分布多粒徑隨機排列樣本波前形狀圖Fig.16 Wavefront shape in randomly arranged samples of uniformly distributed multi-size particles

3 材料臨邊界區域的變形特征

下面從材料臨邊界區域內顆粒之間的接觸關系和相對運動出發,分析應力波反射過程中材料的變形特征.這里主要分析密排顆粒樣本,A 類邊界θ=0°時,下邊界附近區域中顆粒之間的力鏈如圖17 所示.

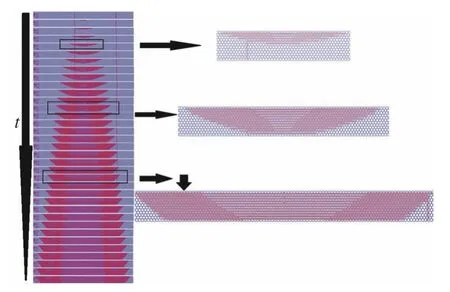
圖17 臨邊界區域力鏈隨時間的演化Fig.17 Evolution of force chain in the pro-border zone over time

注意:由于材料中顆粒按密排方式排列,每個顆粒都與周圍的6 個顆粒發生接觸,初始接觸力為0.隨著材料受到點沖擊作用,產生的應力波隨著時間由激勵點向四周傳播,顆粒之間發生相對位移,于是接觸力鏈的結構發生改變.這才是真實的波最前端,第二部分顯示的波形狀是由速度分布來表示的.根據顆粒振動規律,真實波前應當比圖中所顯示的略大,在之前的工作[33]中已經比較過應力波傳播范圍和顆粒運動(等效應變)之間的關系,并定義了“激活區”.事實上最準確的波前形狀應當由顆粒之間接觸力網絡的變化來確定,但是由于接觸力鏈的拓撲關系(連接或斷開)的改變,無法有效區分初始波和反射波,所以力鏈圖適合用來研究未經擾動的無限大體中波的傳播問題.

力鏈圖的優點是提供了接觸力的方向,如圖18所示,當應力波剛剛進入臨邊界區時,激活區中間部分顆粒之間的力鏈網絡胞元為菱形,主要接觸力的貢獻在豎直方向;激活區其余部分顆粒之間的力鏈網絡胞元為正六邊形(或正三角形),根據后續傳播路徑(圖17)判斷,(以右半為例)主要接觸力的貢獻在正六邊形的右和右下分枝.于是力鏈網絡整體表現為中間向下,兩邊向下向外擴展的形式,這與第2 節中波傳播速度以及動能分布是一致的.

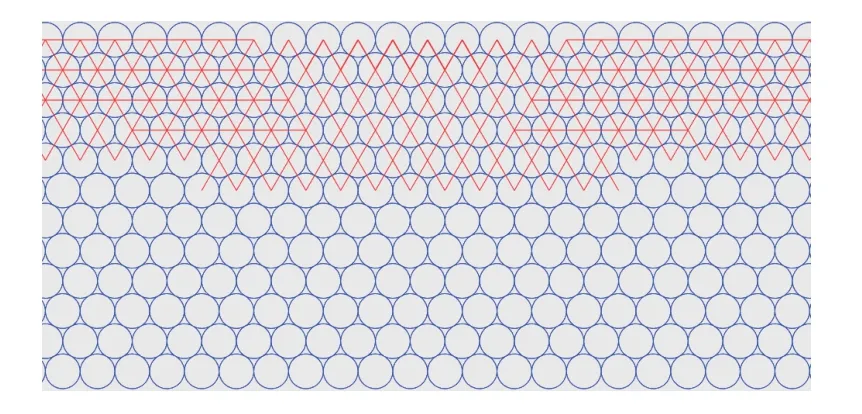
圖18 應力波進入臨邊界區時力鏈網絡Fig.18 Force chain network when stress wave enters the pro-border zone

圖19 顯示了應力波經過邊界反射之后,臨邊界區域的力鏈分布圖.也分為兩個不同的區域:中間區域,力鏈胞元為菱形;兩翼區域,力鏈胞元為正六邊形.似乎與反射前的力鏈分布(圖18)沒有區別,但仔細觀察臨邊界區域力鏈隨時間的演化圖17,發現中間區域和兩翼區域的分界線的凸向發生了改變:當應力波剛剛進入臨邊界區域時,分界線上凸;當應力波經邊界反射之后,分界線下凸.

圖19 應力波反射后臨邊界區力鏈網絡Fig.19 Force chain network in the pro-border zone after stress wave reflection

下面結合動能分布圖來進一步說明,如圖20 所示,分別顯示了應力波反射前后臨邊界區域顆粒動能的分布.由圖可知,兩翼部分具有最大動能,動能等值線的最大梯度方向與波前形狀的分布是一致的.此外,從動能分布上能直觀反映出“反射滯后”現象,臨邊界區域內顆粒與邊界接觸并反彈的過程對應著能量(動能)的存儲和釋放.

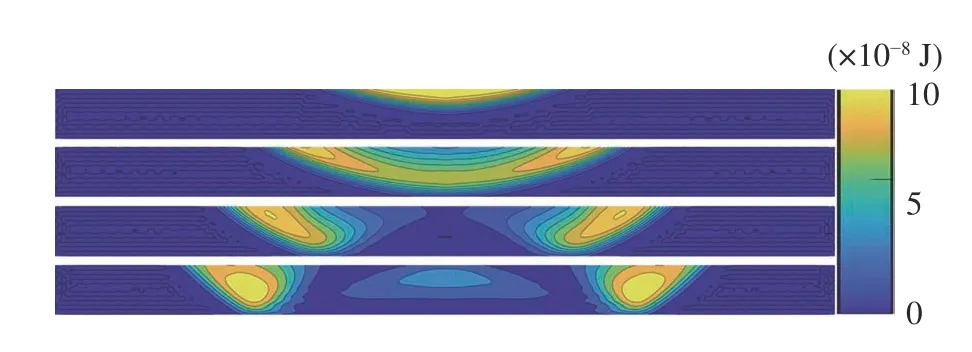
圖20 應力波反射前后臨邊界區顆粒動能分布Fig.20 Distribution of particle kinetic energy in the pro-border zone before and after stress wave reflection

4 結論

本文首先從一維顆粒鏈中應力波的傳播出發,考慮離散元計算中常用的兩種接觸本構關系,定義了臨邊界區域的范圍.然后討論了不同邊界形狀條件下,二維顆粒樣本受沖擊載荷作用時的動力響應,對波在臨邊界區域中的傳播進行了細致的分析,得出如下結論:

(1) 顆粒排列方式和邊界形狀是影響邊界反射的兩個重要因素.二維密排顆粒樣本在水平邊界處的反射表現為逐漸收縮的圓弧;在豎直邊界處的反射表現為直線波前形狀.

(2) 臨邊界區顆粒排列方式的影響可以概括為兩方面:顆粒的相對位置和局部孔隙率.臨邊界區內應力波的反射可以進行簡化,反射后的應力波直接以邊界形狀在臨邊界區內傳播.該結論在邊界情況越復雜(高局部孔隙率,顆粒無序隨機排列)時,越準確.中心區域(臨邊界區域外)的波前形狀主要由波速決定.

(3) 應力波在臨邊界區域中傳播時會出現“反射滯后”現象,顆粒與邊界接觸并反彈的過程對應著能量(動能)的存儲和釋放.經過臨邊界區域的彌散作用,主波動能通常會和緊隨其后的次級波動能一起發生反射.

(4) 圓邊界的匯聚作用和臨邊界區域內顆粒的排列方式是兩個競爭因素,共同決定臨邊界區域內波的反射過程.