面向精密氣磁隔振的磁斥力負(fù)剛度裝置的優(yōu)化設(shè)計(jì)
趙亞敏,崔俊寧,鄒麗敏,邊星元
(1.哈爾濱工業(yè)大學(xué) 超精密光電儀器工程研究所,哈爾濱 150080;2.哈爾濱工業(yè)大學(xué) 超精密儀器技術(shù)及智能化工信部重點(diǎn)實(shí)驗(yàn)室,哈爾濱 150080)
氣浮隔振器因其承載大,固有頻率低且基本不隨隔振負(fù)載變化等特點(diǎn)廣泛應(yīng)用于精密儀器、設(shè)備的隔微振技術(shù)領(lǐng)域[1-3]。隨著高端精密/超精密加工、測(cè)量設(shè)備精度需求的提高,隔振負(fù)載兼具大承載、體積龐大與結(jié)構(gòu)復(fù)雜等特點(diǎn),且對(duì)工作環(huán)境中的低頻微幅振動(dòng)干擾的隔離提出了越來(lái)越嚴(yán)苛的要求[4-5]。并聯(lián)負(fù)剛度裝置可在保證隔振器承載的條件下,進(jìn)一步降低固有頻率、提升低頻隔振性能[6-9]。為穩(wěn)定地實(shí)現(xiàn)大承載下的低頻/超低頻隔振效果,不僅要求負(fù)剛度裝置具有高幅值負(fù)剛度特性,以最大程度的抵消氣浮隔振器的正剛度,實(shí)現(xiàn)近零剛度特性;并且要求負(fù)剛度裝置具有高線性特性以保證隔振系統(tǒng)的穩(wěn)定性。實(shí)現(xiàn)負(fù)剛度裝置的高幅值、高線性負(fù)剛度特性是目前研究的一個(gè)難點(diǎn)。永磁式負(fù)剛度裝置由磁材料的特殊配置構(gòu)成,相比于歐壓連桿[10]、凸輪滾子彈簧[11-13]、倒立擺[14]等負(fù)剛度裝置,具有無(wú)摩擦、結(jié)構(gòu)緊湊、易于與主動(dòng)控制系統(tǒng)集成等特點(diǎn),廣泛用于與正剛度結(jié)構(gòu)并聯(lián)構(gòu)建低頻/超低頻隔振器。
Nijsse[15]利用三塊立方永磁體間的磁力作用設(shè)計(jì)了磁引力與磁斥力兩種負(fù)剛度結(jié)構(gòu)。Carrella等[16]與Wang等[17]分別將三塊立方永磁體構(gòu)成的磁引力負(fù)剛度裝置與螺旋彈簧、空氣彈簧并聯(lián)實(shí)現(xiàn)低頻隔振效果。Wu等[18]試驗(yàn)驗(yàn)證了磁斥力負(fù)剛度裝置的性能。戴鵬輝[19]將兩種負(fù)剛度裝置并聯(lián)實(shí)現(xiàn)寬域高線性負(fù)剛度特性。Dong等[20]將磁引力負(fù)剛度裝置中的立方永磁體替換為環(huán)形永磁體,并基于等效磁荷模型建立了負(fù)剛度裝置的剛度與剛度非線性度解析模型。Shan等[21]利用由吸引布置的四塊立方永磁體構(gòu)成的負(fù)剛度裝置隔離地面低頻振動(dòng)干擾;Oyelade[22]利用排斥布置的四塊立方永磁體設(shè)計(jì)了負(fù)剛度裝置,并對(duì)其動(dòng)力學(xué)特性進(jìn)行了研究。立方永磁體負(fù)剛度裝置的剛度可通過磁鐵間距調(diào)節(jié)、磁阻尼小、高頻段隔振性能優(yōu)越,但是磁引力負(fù)剛度裝置的磁鐵間距與振動(dòng)位移方向相同,限制了隔振負(fù)載的振幅[23]。Zheng等[24-26]利用兩個(gè)同軸嵌套的磁環(huán)構(gòu)成負(fù)剛度裝置,并給出了磁環(huán)負(fù)剛度裝置的優(yōu)化設(shè)計(jì)流程。Zhou等[27-28]將雙磁環(huán)負(fù)剛度裝置用于解決新生兒運(yùn)輸過程中的超低頻隔振問題。磁環(huán)負(fù)剛度裝置產(chǎn)生的高磁阻尼無(wú)法改善高頻段的振動(dòng)傳遞率,且磁環(huán)結(jié)構(gòu)確定后剛度不可調(diào)整,無(wú)法適應(yīng)載荷質(zhì)量及激勵(lì)頻率的變化[29]。
針對(duì)磁環(huán)負(fù)剛度裝置剛度不可調(diào)、立方永磁體構(gòu)成的磁引力負(fù)剛度裝置限制隔振負(fù)載振動(dòng)幅值的問題,提出了一種由三個(gè)沿垂向同向磁化的立方永磁體構(gòu)成的磁斥力負(fù)剛度裝置。磁斥力負(fù)剛度裝置的剛度通過磁鐵間距調(diào)整,且磁鐵間距與振動(dòng)位移的方向相互垂直,不受隔振負(fù)載振幅的影響。建立磁斥力負(fù)剛度裝置的解析模型,采用遺傳算法實(shí)現(xiàn)高幅值、高線性負(fù)剛度特性的優(yōu)化設(shè)計(jì)。論文的后續(xù)研究?jī)?nèi)容如下:首先,基于等效磁荷模型,建立磁斥力負(fù)剛度裝置的磁力、剛度及剛度非線性解析模型,并仿真驗(yàn)證理論模型的正確性。然后,采用遺傳算法優(yōu)化幾何參數(shù),給出優(yōu)化設(shè)計(jì)結(jié)論。
1 磁斥力負(fù)剛度裝置及理論建模
1.1 磁斥力負(fù)剛度裝置
由磁斥力負(fù)剛度裝置與氣浮隔振器并聯(lián)構(gòu)成的氣磁隔振器的原理如圖1所示。氣浮隔振器由主氣室、附加氣室與彈性膜構(gòu)成,主、附氣室間通過節(jié)流孔連接。磁斥力負(fù)剛度裝置由沿垂向同向磁化的左側(cè)永磁體、中間永磁體與右側(cè)永磁體構(gòu)成,與氣浮隔振器并聯(lián)支撐隔振負(fù)載。中間永磁體與隔振負(fù)載固定連接,左側(cè)永磁體與右側(cè)永磁體幾何尺寸相同、對(duì)稱固定在中間永磁體兩側(cè)。中間永磁體與左、右側(cè)永磁體的Z向、水平Y(jié)向中心重合,水平X向間距為h。通過氣浮隔振器充氣壓力的改變保證隔振負(fù)載及激勵(lì)頻率變化時(shí),中間永磁體的Z向高度中心始終與左、右永磁體等高。此外,在高集成度的應(yīng)用場(chǎng)合,也可將磁斥力負(fù)剛度裝置集成到氣浮隔振器的內(nèi)部。
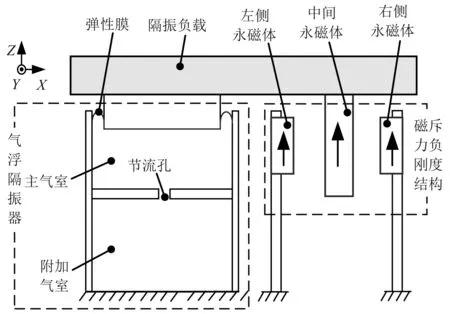
圖1 磁斥力負(fù)剛度裝置與氣浮隔振器并聯(lián)構(gòu)成的氣磁隔振器Fig.1 Air magnetic vibration isolator composed of negative stiffness device with magnetic repulsion and air floating vibration isolator
由于結(jié)構(gòu)的對(duì)稱性,在圖2所示的靜平衡點(diǎn)處(z=0),左、右側(cè)永磁體施加在中間永磁體上的磁斥力相互抵消。微小擾動(dòng)作用下,中間永磁體偏離靜平衡點(diǎn)運(yùn)動(dòng)(z≠0),左、右側(cè)永磁體產(chǎn)生與運(yùn)動(dòng)方向相同的磁斥力使中間永磁體繼續(xù)偏離靜平衡點(diǎn)運(yùn)動(dòng);無(wú)外力作用下,中間永磁體將不會(huì)回到靜平衡點(diǎn)。因此,中間永磁體在Z向呈現(xiàn)負(fù)剛度特性,可抵消彈簧的正剛度,實(shí)現(xiàn)高靜低動(dòng)剛度特性,提升氣浮隔振器的低頻隔振性能。
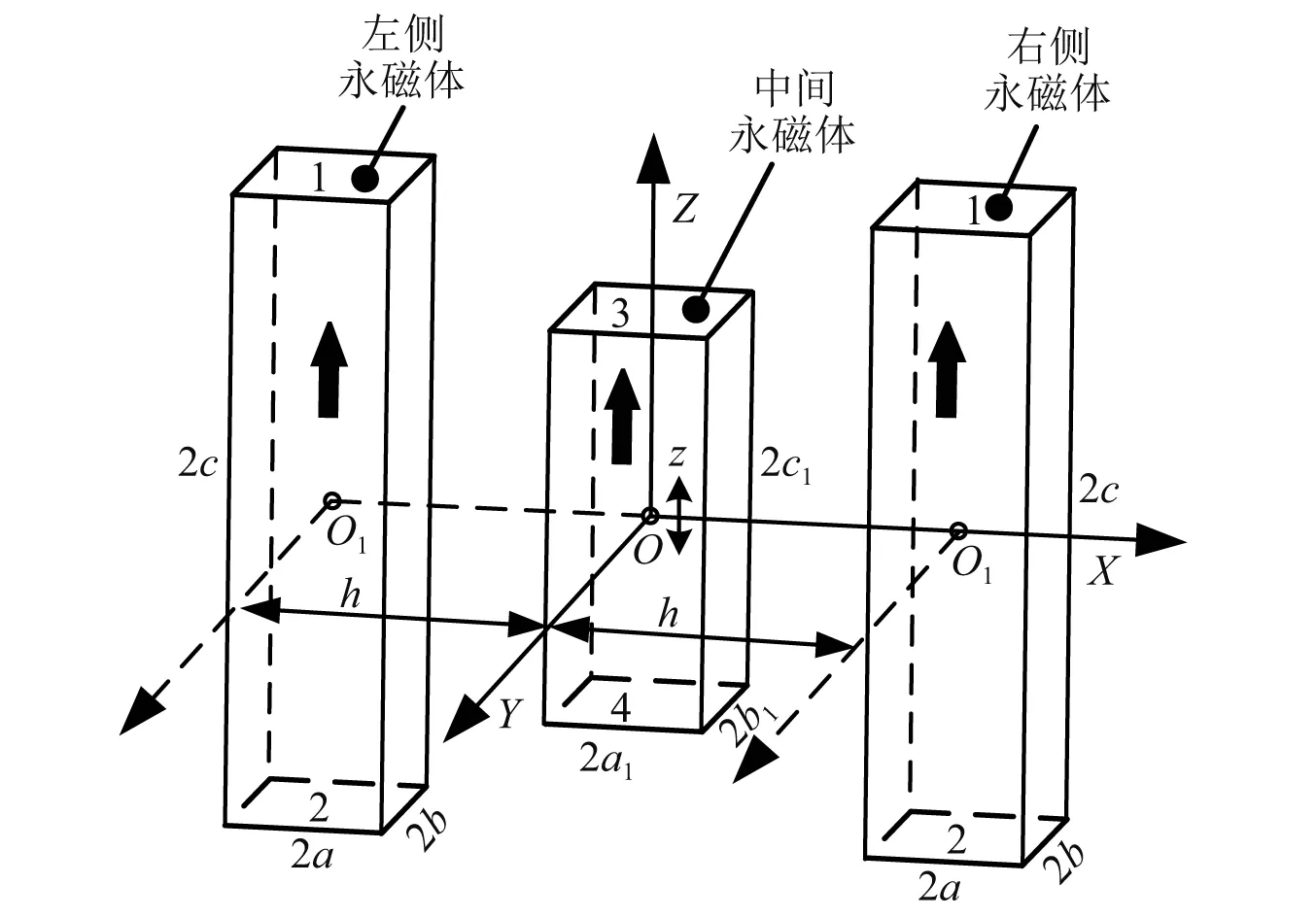
圖2 磁斥力負(fù)剛度裝置的原理圖Fig.2 Schematic diagram of the negative stiffness device with magnetic repulsion
本文重點(diǎn)研究磁斥力負(fù)剛度裝置的設(shè)計(jì)及優(yōu)化問題,將氣浮隔微振器等效為線性彈簧,且精密儀器設(shè)備所處環(huán)境中的低頻微幅振動(dòng)干擾通常在±1 mm范圍內(nèi),在此微振動(dòng)干擾下,通常不考慮氣浮隔微振器的非線性特性。
1.2 磁力理論建模
根據(jù)等效磁荷法原理,左側(cè)永磁體施加在中間永磁體上的磁力等于表面3、表面4上的磁荷與表面1、表面2上的磁荷間相互作用力的疊加。由于結(jié)構(gòu)對(duì)稱,中間永磁體所受Z向磁力等于左側(cè)永磁體與中間永磁體間Z向磁力的2倍。設(shè)同極性磁荷間作用力為正,異極性磁荷間作用力為負(fù),中間永磁體所受Z向磁力F為
F=2(F13+F24-F14-F23)
(1)
Fmn(m=1,2;n=3,4)為表面m施加在表面n上的Z向磁力。以F13為例推導(dǎo)中間永磁體所受Z向磁力。中間永磁體的長(zhǎng)、寬、高分別為2a1,2b1,2c1,左、右側(cè)永磁體的長(zhǎng)、寬、高分別為2a,2b,2c。中間永磁體的中心O與左側(cè)永磁體的中心O1的相對(duì)位移為h,0,z。以中間永磁體的中心O建立坐標(biāo)系,左側(cè)永磁體的中心O1的坐標(biāo)為(-h,0,0)。在表面1坐標(biāo)(-h+α,β,c)處取微元Q,微元Q的磁荷為Brdαdβ,Br為表面1的剩余磁感應(yīng)強(qiáng)度;在表面3坐標(biāo)(α1,β1,z+c1)處取微元P,微元P的磁荷為Br1dα1dβ1,Br1為表面3的剩余磁感應(yīng)強(qiáng)度。微元Q施加在微元P上的Z向磁力為
(2)
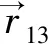
(3)
(4)
(5)
(6)
聯(lián)立式(1)與式(3)~式(6)可得Z向磁力F
(7)
其中:
u=z+(-1)qc1-(-1)pc,v=(h+α1-α)2+(β1-β)2+u2。
四重積分后得
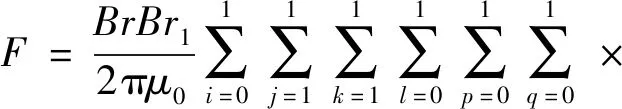
(8)
其中:
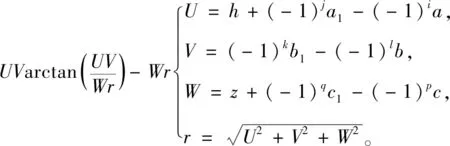
1.3 有限元仿真驗(yàn)證
采用maxwell電磁軟件的3維建模仿真驗(yàn)證所建理論模型的正確性,磁斥力負(fù)剛度裝置的幾何參數(shù)如表1所示,Br=Br1=1.34 T為永磁體的剩余磁感應(yīng)強(qiáng)度,μr=1.023為相對(duì)磁導(dǎo)率。磁鐵間距h=20 mm時(shí),磁斥力負(fù)剛度裝置靜平衡點(diǎn)的磁感應(yīng)強(qiáng)度云圖如圖3所示。不同磁鐵間距下,有限元仿真與理論計(jì)算得到的磁力-位移曲線如圖4所示。中間永磁體偏離平衡位置±10 mm,理論計(jì)算與有限元仿真的偏差小于10%,驗(yàn)證了所建理論模型的正確性。

表1 磁斥力負(fù)剛度裝置的幾何參數(shù)Tab.1 Geometric parameters of negative stiffness device with magnetic repulsion mm
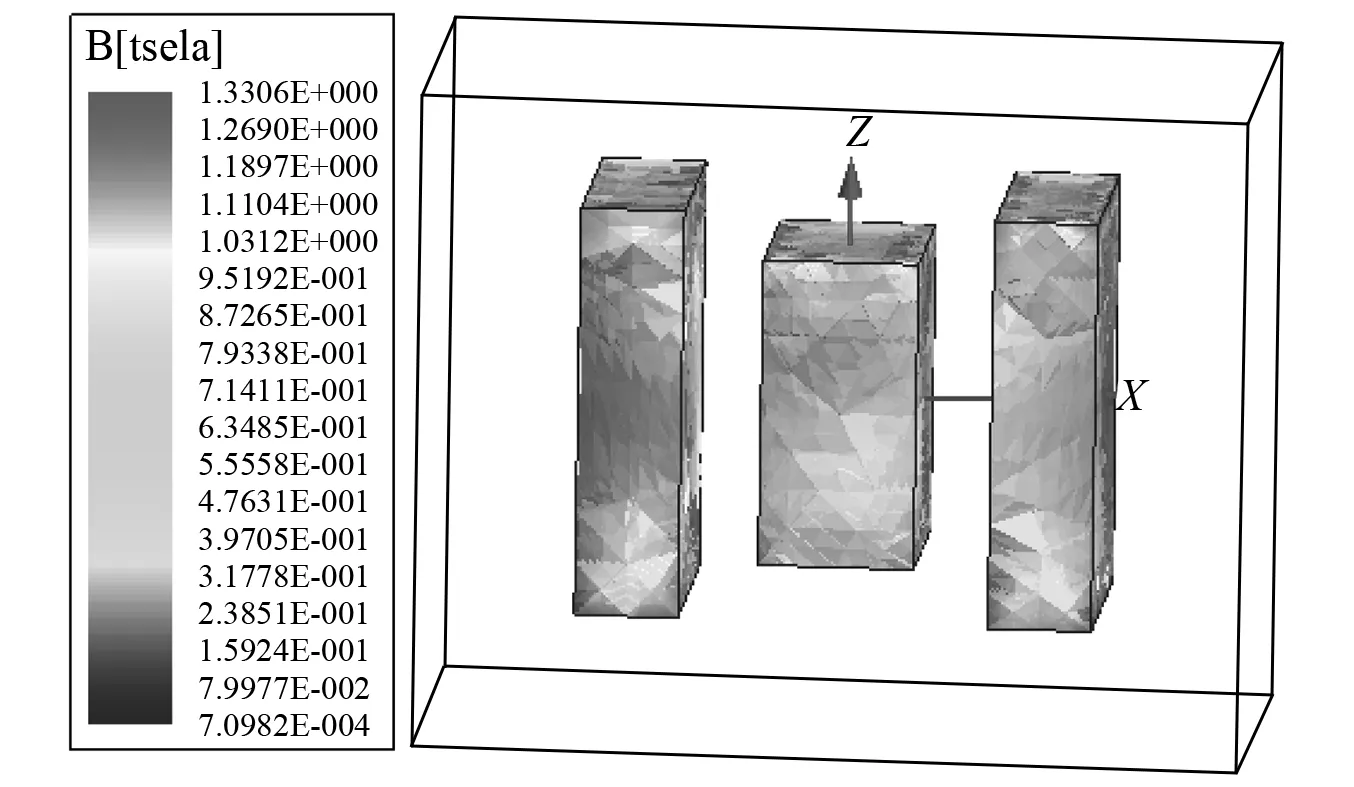
圖3 磁斥力負(fù)剛度裝置靜平衡點(diǎn)的磁感應(yīng)強(qiáng)度云圖Fig.3 Magnetic induction intensity cloud diagram at static equilibrium point of negative stiffness device with magnetic repulsion
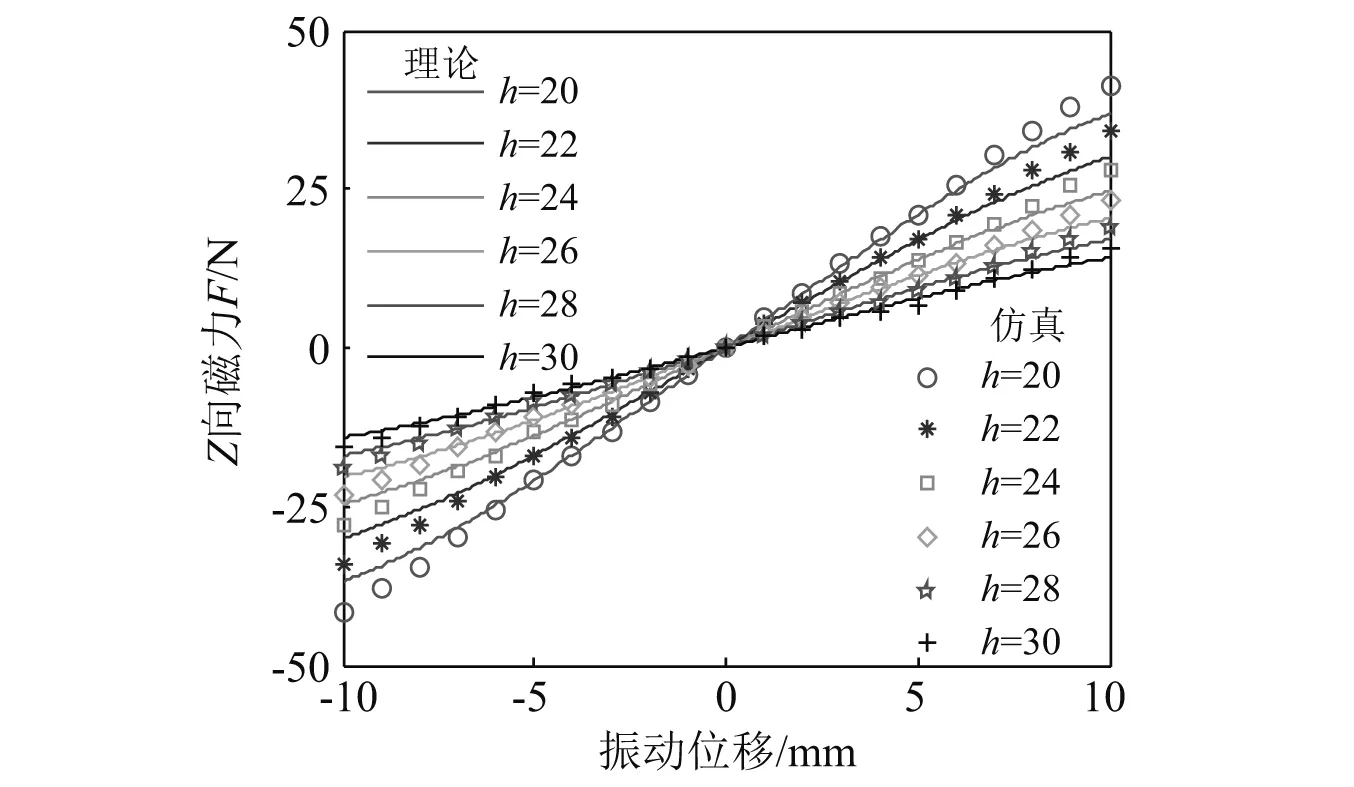
圖4 磁斥力負(fù)剛度裝置的磁力-位移曲線Fig.4 Magnetic force-displacement curve of negative stiffness device with magnetic repulsion
由式(8)計(jì)算得到磁斥力負(fù)剛度裝置的Z向磁力隨振動(dòng)位移z與磁鐵間距h變化的三維曲線如圖5所示。中間永磁體所受的Z向磁力隨磁鐵間距h的變化呈現(xiàn)較強(qiáng)的非線性特性,而在沿Z向的小區(qū)間振動(dòng)范圍內(nèi),則具有近似線性的Z向磁力-振動(dòng)位移關(guān)系。
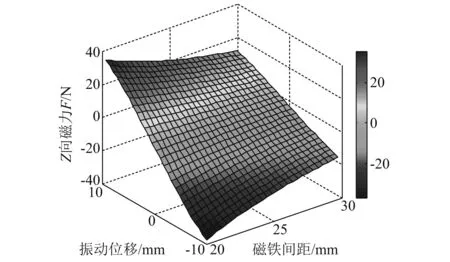
圖5 Z向磁力Fig.5 Magnetic force along Z axis of negative stiffness device with magnetic repulsion
1.4 剛度與剛度非線性度
根據(jù)剛度的定義,將磁力F對(duì)位移z取負(fù)導(dǎo)數(shù)得
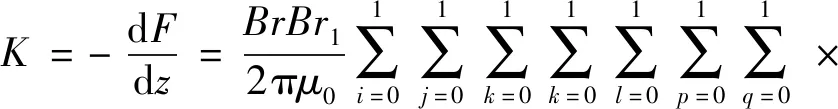
(9)
負(fù)號(hào)說(shuō)明回復(fù)力的方向與磁力方向相反,其中,φ(U,V,W,r)=2r+Vln(r-V)+Uln(r-U),U,V,W,r的取值與式(8)相同。
由式(9)可知,磁斥力負(fù)剛度裝置的剛度表示為中間永磁體振動(dòng)位移z的非線性函數(shù),隨振動(dòng)位移而變化。剛度非線性度定義為偏離靜平衡點(diǎn)負(fù)剛度值的程度,即
η=|(K-Kq)/Kq|×100%
(10)
式中:K=K(z)|z≠0為z處的剛度;Kq=K(z)|z=0為靜平衡點(diǎn)剛度。
超精密儀器設(shè)備的低頻/超低頻隔振系統(tǒng)要求負(fù)剛度裝置不僅具有高幅值負(fù)剛度,并且具有高剛度線性度,以保證隔振系統(tǒng)的穩(wěn)定性。選定中間永磁體的長(zhǎng)×寬×高(2a1×2b1×2c1)為15 mm×20 mm×30 mm,左、右側(cè)永磁體的長(zhǎng)×寬×高(2a×2b×2c)為10 mm×25 mm×40 mm,磁鐵間距h在20~30 mm,Br=Br1=1.34 T,由式(9)和式(10)計(jì)算剛度與剛度非線性度。由圖6所示的特性曲線可知,磁斥力負(fù)剛度裝置呈現(xiàn)較強(qiáng)的非線性。磁鐵間距越小、振動(dòng)幅值越大,非線性越明顯。增大磁鐵間距可降低剛度非線性,但會(huì)導(dǎo)致負(fù)剛度幅值降低。因此,調(diào)整磁鐵間距無(wú)法兼顧磁斥力負(fù)剛度裝置的負(fù)剛度幅值與剛度線性度,實(shí)際使用過程中需根據(jù)特定需求對(duì)兩個(gè)指標(biāo)進(jìn)行取舍。
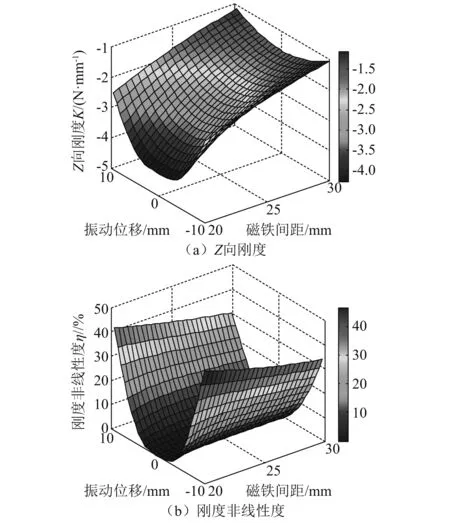
圖6 磁斥力負(fù)剛度裝置的特性曲線Fig.6 Characteristic curve of negative stiffness device with magnetic repulsion
2 磁斥力負(fù)剛度裝置的優(yōu)化設(shè)計(jì)
由式(9)與式(10)可知,磁斥力負(fù)剛度裝置的剛度及剛度非線性度均與永磁體的幾何尺寸有關(guān)。合適的幾何參數(shù)可實(shí)現(xiàn)高幅值、高線性負(fù)剛度特性。由圖6可知,較小的磁鐵間距及永磁體X向尺寸可保證負(fù)剛度幅值;此外,沿Y軸陣列布置多個(gè)磁斥力負(fù)剛度裝置、采用并聯(lián)的方式增大負(fù)剛度幅值,要求永磁體具有較小的Y向尺寸;因此,給定中間永磁體的長(zhǎng)×寬×高(2a1×2b1×2c1)為15 mm×20 mm×30 mm。考慮結(jié)構(gòu)的緊湊性及裝調(diào)空間,左、右側(cè)永磁體的尺寸滿足6≤2a≤15 mm,2b≥21 mm,2c≥31 mm,磁鐵間距h≥20 mm,磁斥力負(fù)剛度裝置的整體尺寸小于70 mm×40 mm×50 mm,即
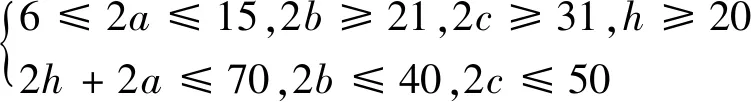
(11)
根據(jù)上述約束條件得到自變量的取值范圍如表2所示。環(huán)境微振動(dòng)引起精密儀器設(shè)備中隔振負(fù)載的垂向振動(dòng)位移通常在±1 mm;磁斥力負(fù)剛度裝置的負(fù)剛度幅值隨振動(dòng)位移的增大而減小,剛度非線性度隨振動(dòng)位移的增大而增大。因此,將靜平衡點(diǎn)剛度與±1 mm處的剛度非線性度作為目標(biāo)函數(shù),采用遺傳算法優(yōu)化左、右側(cè)永磁體的幾何參數(shù)與磁鐵間距。

表2 自變量的取值范圍Tab.2 The range of independent variables
2.1 以靜平衡點(diǎn)剛度為目標(biāo)函數(shù)的優(yōu)化
將靜平衡點(diǎn)剛度作為目標(biāo)函數(shù)對(duì)磁斥力負(fù)剛度裝置的幾何參數(shù)進(jìn)行優(yōu)化,優(yōu)化負(fù)剛度及其幾何參數(shù)如表3所示。優(yōu)化后,磁斥力負(fù)剛度裝置的負(fù)剛度幅值增大251.33%,剛度非線性度提高兩個(gè)數(shù)量級(jí)。因此,將靜平衡點(diǎn)剛度作為目標(biāo)函數(shù)的優(yōu)化可在犧牲剛度線性度的條件下提高負(fù)剛度幅值。

表3 靜平衡點(diǎn)剛度作為目標(biāo)函數(shù)的優(yōu)化結(jié)果Tab.3 Optimization result with the objective function of stiffness at static equilibrium
2.2 以±1 mm處的剛度非線性度為目標(biāo)函數(shù)的優(yōu)化
將±1 mm處的剛度非線性度作為目標(biāo)函數(shù)對(duì)磁斥力負(fù)剛度裝置的幾何參數(shù)進(jìn)行優(yōu)化,優(yōu)化剛度非線性度及其幾何參數(shù)如表4所示。優(yōu)化后,±1 mm處的剛度非線性度降低八個(gè)數(shù)量級(jí),負(fù)剛度幅值降低33.99%。因此,以±1 mm處的剛度非線性度為目標(biāo)函數(shù)的優(yōu)化同樣無(wú)法兼顧磁斥力負(fù)剛度裝置的高幅值與高線性特性。
對(duì)比表3與表4可知,采用單目標(biāo)函數(shù)優(yōu)化磁斥力負(fù)剛度裝置的幾何參數(shù)時(shí),優(yōu)化目標(biāo)的改變對(duì)幾何參數(shù)的影響較大,靜平衡點(diǎn)剛度與±1 mm處的剛度非線性度此消彼長(zhǎng)。
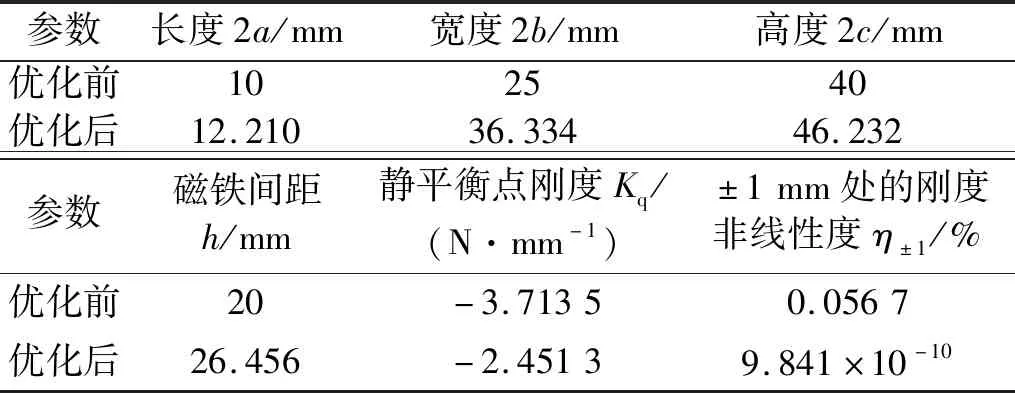
表4 ±1 mm處的剛度非線性度作為目標(biāo)函數(shù)的優(yōu)化結(jié)果Tab.4 Optimization result with the objective function of stiffness nonlinearity at ±1 mm
如圖7所示,c=20 mm,h=20 mm時(shí),靜平衡點(diǎn)剛度與±1 mm處的剛度非線性度兩個(gè)目標(biāo)函數(shù)的極值點(diǎn)對(duì)應(yīng)的幾何參數(shù)不同;靜平衡點(diǎn)剛度隨左、右側(cè)永磁體長(zhǎng)度與寬度的增大而增大,而±1 mm處的剛度非線性度隨左、右側(cè)永磁體長(zhǎng)度的增大先減小后增大;左、右側(cè)永磁體長(zhǎng)度較小時(shí),±1 mm處的剛度非線性度隨永磁體寬度的增大而增大;永磁體長(zhǎng)度超過一定值后,變化規(guī)律相反。因此,單目標(biāo)函數(shù)優(yōu)化無(wú)法兼顧高幅值、高線性負(fù)剛度特性,需要對(duì)兩個(gè)目標(biāo)函數(shù)進(jìn)行協(xié)調(diào)。
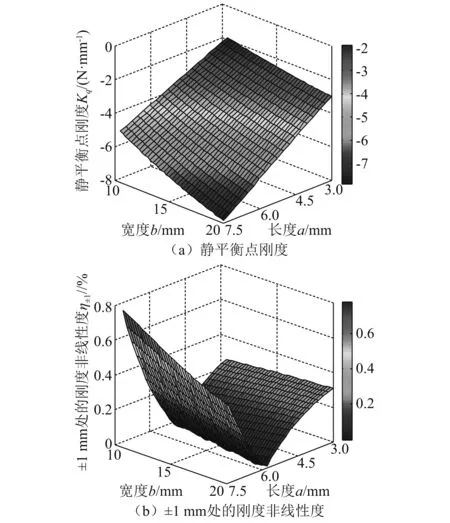
圖7 左、右側(cè)永磁體的長(zhǎng)度和寬度對(duì)磁斥力負(fù)剛度裝置的影響Fig.7 Influences of the length and width of the left or right permanent magnet on the negative stiffness device with magnetic repulsion
2.3 多目標(biāo)優(yōu)化
靜平衡點(diǎn)剛度和±1 mm處的剛度非線性度具有不同的單位和數(shù)量級(jí),采用式(12)與式(13)所示的利差方法分別對(duì)其進(jìn)行歸一化處理,以實(shí)現(xiàn)多目標(biāo)函數(shù)的協(xié)調(diào)。
(12)
(13)
將靜平衡點(diǎn)剛度作為目標(biāo)函數(shù)優(yōu)化得到Kqmin=-13.046 6 N/mm,Kqmax=-0.567 985 N/mm;將±1 mm處的剛度非線性度作為目標(biāo)函數(shù)優(yōu)化得到η±1min=9.841×10-10%,η±1max=3.941 35%。無(wú)量綱處理后,根據(jù)兩個(gè)優(yōu)化目標(biāo)對(duì)最終目標(biāo)函數(shù)的影響程度為其分配權(quán)重系數(shù)w1,w2,w1,w2>0,且w1+w2=1,采用線性加權(quán)的方式將兩個(gè)優(yōu)化目標(biāo)組合成單目標(biāo)函數(shù)g
g=w1K′+w2η′±1
(14)
按照表5中的權(quán)重系數(shù)分配方式優(yōu)化磁斥力負(fù)剛度裝置,由表6所示的優(yōu)化結(jié)果可知,權(quán)重系數(shù)的改變對(duì)左、右側(cè)永磁體長(zhǎng)度和寬度的影響較小,而對(duì)永磁體高度的影響較大。靜平衡點(diǎn)剛度權(quán)重系數(shù)較小時(shí),左、右側(cè)永磁體的高度2c取38.266 mm,可在保證負(fù)剛度線性度的基礎(chǔ)上提高負(fù)剛度幅值;靜平衡點(diǎn)剛度權(quán)重系數(shù)較大時(shí),永磁體高度取15.5 mm,有利于提高負(fù)剛度幅值,但會(huì)導(dǎo)致磁斥力負(fù)剛度裝置呈現(xiàn)強(qiáng)非線性特性。第2組與第3組、第4組與第5組的優(yōu)化結(jié)果相同,說(shuō)明對(duì)應(yīng)幾何參數(shù)下的歸一化剛度非線性度遠(yuǎn)大于歸一化負(fù)剛度。對(duì)比各組優(yōu)化結(jié)果可知,第3組權(quán)重系數(shù)為最佳分配方式,靜平衡點(diǎn)剛度大于9 N/mm,±1 mm處的剛度非線性度優(yōu)于0.000 15%,負(fù)剛度幅值與剛度線性度較優(yōu)化前均有顯著提升。考慮實(shí)際加工與裝配精度,將磁斥力負(fù)剛度裝置的幾何尺寸保留一位小數(shù),即2a=15.0 mm,2b=4.0 mm,2c=38.3 mm,h=20.0 mm,計(jì)算得到靜平衡點(diǎn)剛度為-9.138 5 N/mm,±1 mm處的剛度非線性度為0.020 2%。優(yōu)化前后磁斥力負(fù)剛度結(jié)構(gòu)的性能對(duì)比如圖8所示,優(yōu)化后,靜平衡點(diǎn)剛度提升146.09%,±1 mm處的剛度非線性度降低64.73%。

表5 權(quán)重系數(shù)分配方式Tab.5 Weight coefficient allocation method
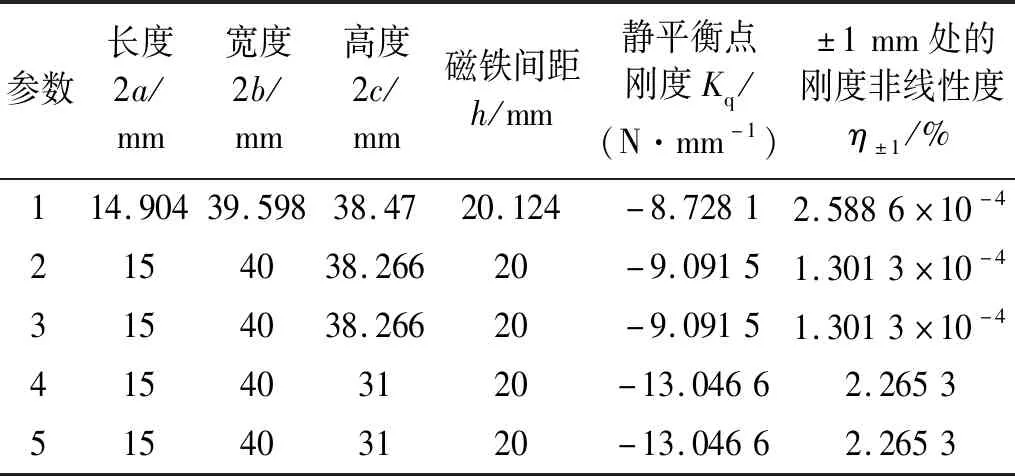
表6 不同權(quán)重下的多目標(biāo)優(yōu)化結(jié)果Tab.6 Multi-objective optimization results at different weight coefficients
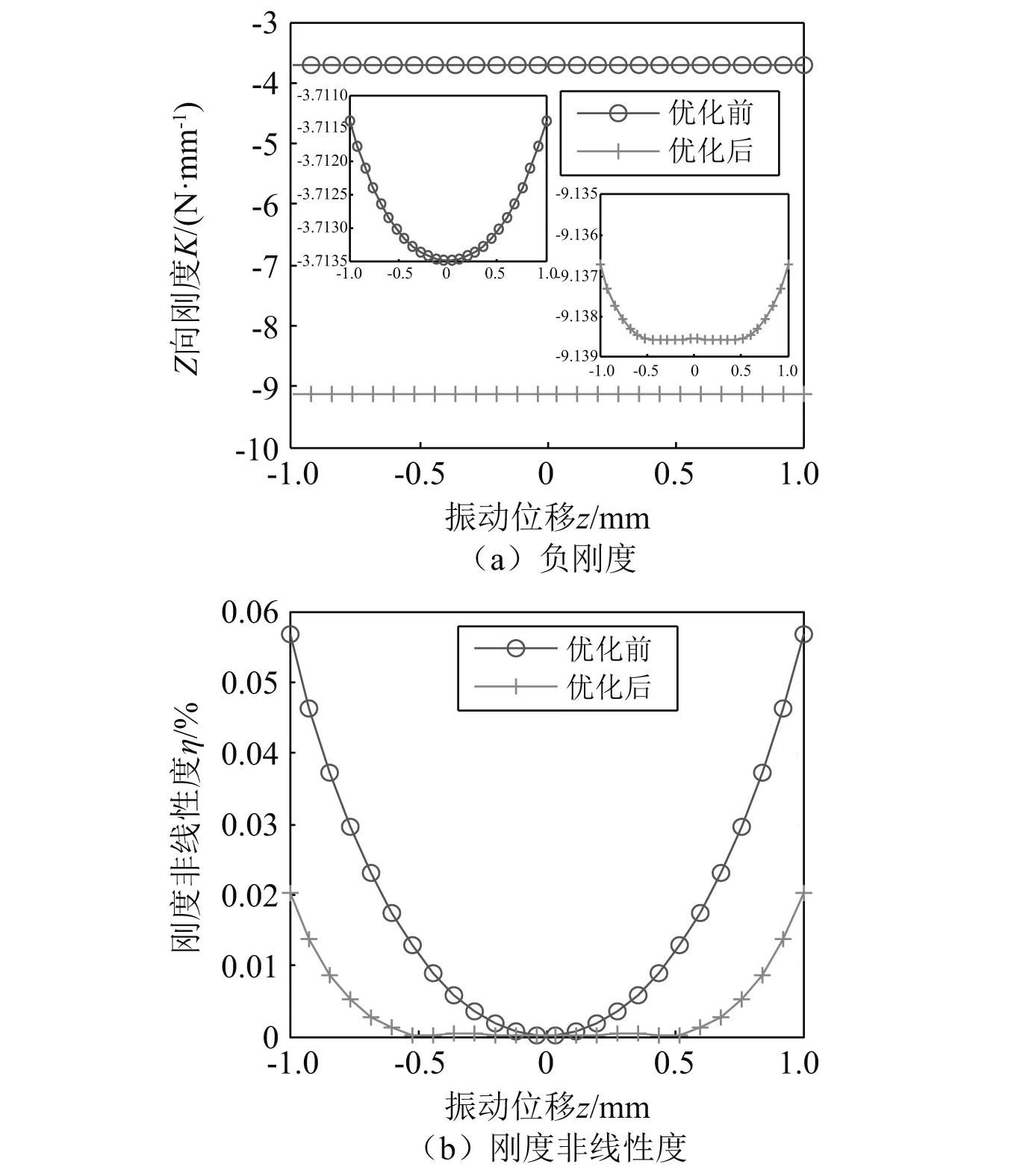
圖8 優(yōu)化前后磁斥力負(fù)剛度裝置的剛度與剛度非線性度Fig.8 Negative stiffness and stiffness nonlinearity of negative stiffness device with magnetic repulsion before and after optimization
實(shí)際工程應(yīng)用中,需要根據(jù)氣浮隔微振器的正剛度值對(duì)磁斥力負(fù)剛度裝置的負(fù)剛度值的范圍進(jìn)行約束,以保證并聯(lián)構(gòu)成的氣磁隔振器的剛度值接近于零、但大于零,處于穩(wěn)定狀態(tài)。
3 結(jié) 論
本文提出了一種面向精密氣磁隔振的磁斥力負(fù)剛度裝置,以進(jìn)一步提升氣浮隔振器的低頻性能、降低環(huán)境中的低頻微幅振動(dòng)干擾對(duì)高端精密加工、測(cè)量設(shè)備的影響。磁斥力負(fù)剛度裝置由三塊沿垂向同向磁化的立方永磁體水平布置構(gòu)成,剛度值可通過磁鐵間距調(diào)整。基于等效磁荷模型建立磁斥力負(fù)剛度裝置的磁力、剛度及剛度非線性解析模型,并采用遺傳算法對(duì)永磁體的幾何參數(shù)進(jìn)行優(yōu)化設(shè)計(jì)。通過研究得出以下結(jié)論:
(1)采用單目標(biāo)函數(shù)優(yōu)化磁斥力負(fù)剛度裝置的幾何參數(shù)無(wú)法兼顧高幅值、高線性負(fù)剛度特性,且優(yōu)化目標(biāo)的改變對(duì)幾何參數(shù)的影響較大。以靜平衡點(diǎn)剛度為目標(biāo)函數(shù)的優(yōu)化,將靜平衡點(diǎn)剛度Kq增大251.33%,η±1提高兩個(gè)數(shù)量級(jí);以±1 mm處的剛度非線性度為目標(biāo)函數(shù)的優(yōu)化,將±1 mm處的剛度非線性度η±1降低八個(gè)數(shù)量級(jí),靜平衡點(diǎn)剛度Kq降低33.99%。
(2)以靜平衡點(diǎn)剛度與±1 mm處的剛度非線性度為目標(biāo)函數(shù)的多目標(biāo)優(yōu)化將靜平衡點(diǎn)剛度Kq提升146.09%,±1 mm處的剛度非線性度η±1降低64.73%。
本文的研究實(shí)現(xiàn)了面向精密氣磁隔振的磁斥力負(fù)剛度裝置的高幅值、高線性度的優(yōu)化設(shè)計(jì),不僅可應(yīng)用于精密儀器及系統(tǒng)的氣浮隔振系統(tǒng)中,在超精密制造、尖端科學(xué)實(shí)驗(yàn)系統(tǒng)等領(lǐng)域也均具有重要的應(yīng)用價(jià)值。

