基于動載試驗荷載效率的簡支梁橋沖擊系數研究

周勇軍，趙 洋，趙 煜，曹 群，李 珍

(1.長安大學 公路學院，西安 710064；2.長安大學 公路大型結構安全教育部工程研究中心，西安 710064；3.呼和浩特市市政工程管理局，呼和浩特 010020)

沖擊系數是車輛激勵下，橋梁產生的結構動力效應與相應豎向靜力效應的比值。引入沖擊系數的概念可以有效地將橋梁結構復雜的動力問題靜力化，是研究車橋的耦合作用以及檢測現役橋梁動力性能的重要內容之一。但沖擊系數有很大的隨機性[1]，且受到眾多因素的影響[2]，因此眾多學者對沖擊系數進行了大量的研究與評價。橋面平整度是影響沖擊系數的重要因素，眾多研究表明沖擊系數隨著橋面平整度狀況變差而減小[3-5]。

車輛模型的不斷完善使的車橋耦合振動的更加貼近實際，Wang等[6]提出三軸車輛模型；Obrien等[7]參考歐洲大量卡車統計數據采用五軸車模型；蔣培文等[8]提出了四自由度雙軸平面車輛模型、五自由度三軸平面車輛模型、九自由度三軸空間車輛模型等車輛模型；鄧露等[9]基于中國橋梁規范中的設計車輛荷載，提出了一組5軸車輛模型參數；吳銘漢等[10]對比了移動彈簧-質量、四分之一、二分之一及整車模型的沖擊作用，結果顯示，二分之一車輛模型和整車模型作用下沖擊系數計算良好。

對車輛數和車輛加載位置對沖擊系數影響的研究方面，Huang等[11]發現車輛不同加載位置使混凝土梁橋各主梁上的沖擊系數發生變化；單輛車的靜荷載效應較小，但沖擊系數不一定小，甚至大于規范值[12-13]；研究表明單輛車的沖擊系數比多輛車沖擊系數大[14-15]。

在車重作用分析方面，研究表明沖擊系數隨著車重增加而減小[16]，也有研究認為沖擊系數隨著靜力效應增大而減小[17]，二者規律一致，韓萬水等[18]計算特重車荷載下的沖擊系數，指出特重車荷載下的沖擊系數小于現行規范值。

我國現行規范JTG D60—2015《公路橋涵設計通用規范》中規定沖擊系數的取值僅與橋梁結構基頻有關，計算公式是對6座鋼筋混凝土橋及1座預應力鋼筋混凝土通過現場實測的數據統計回歸分析得到，樣本數較少且種類單一，部分學者也對其適應性進行質疑[19]，現行規范采用均布力加集中力作為橋梁設計荷載形式，無法直接展現移動車輛荷載對橋梁結構的沖擊作用。若要研究設計荷載作用下的沖擊系數，應采用與規范規定的設計荷載標準值相近的車輛荷載或等效的隨機狀態進行研究，而現行規范中規定的車道荷載為均布力和一個集中力，均布力加集中力的車橋耦合振動可以近似的通過數值模擬來實現，但在實測中對于均布力加集中力用車輛荷載無法實現。因此采用現行規范中規定的車道荷載進行沖擊系數分析沒有實際工程價值。

沖擊系數是汽車荷載標準值的放大系數，而不是單一或少數車輛荷載的沖擊作用[20]。上述研究表明，車輛載重較小時，相比重車會產生較大的沖擊系數，而靜載時效應較小，雖然得到沖擊系數較大，但總的荷載效應仍然較小，這樣獲取的沖擊系數沒有實際意義。但在實際橋梁動載試驗中通常僅采用一輛車或兩輛車進行試驗，此時并不是在設計荷載下的標準試驗，缺乏與規范設計值的對比依據。

基于此，本文以標準跨徑簡支小箱梁橋為研究對象，采用橋梁動載試驗常見的三軸重車來等效還原設計車道荷載，考慮跨徑、橋面平整度、速度等因素的影響，進行準設計狀態車橋耦合振動分析，以此研究等效設計荷載作用下的沖擊系數，并與規范值進行對比；其次研究動載試驗荷載效率與沖擊系數的關系，分析不同因素對沖擊系數的影響規律；最后提出基于動載試驗荷載效率的輕荷載沖擊系數修正方法，建立輕荷載試驗沖擊系數與準設計狀態沖擊系數之間的關系，為橋梁動載試驗實測沖擊系數值的評價提供依據。

1 車橋耦合沖擊系數分析理論

1.1 沖擊系數計算方法

公路橋梁設計規范中一般采用動力沖擊系數來表征車輛對橋梁結構產生的動力沖擊效應。沖擊系數是汽車過橋時對橋梁結構產生的豎向動力效應的增大系數。車輛荷載的沖擊系數可表示為：

(1)

式中：Yjmax為在車輛過橋時測得的效應時間歷程曲線上最大靜力效應處量取的最大靜力效應值；Ydmax為在效應時間歷程曲線上最大靜力效應處量取的最大動效應值。

本文采用的最大動力效應由車輛過橋時的撓度時程曲線獲得，最大靜力效應為車輛低速過橋(準靜態)時結構的最大動力效應值。

1.2 車輛模型及振動方程

參考JTG/T J21-01—2015《公路橋梁載荷試驗規程》[21]，本文選擇橋梁動載試驗的主流車型三軸載重車為試驗加載車，采用五自由度三軸平面車輛模型，并選用了盡可能還原荷載試驗中實際三軸載重車的模型參數，車輛模型如圖1所示，模型參數見表1[22]。美國AASHTO橋梁規范中的主要設計車輛HS20-44三軸卡車模型規定懸架力是由線性彈簧的彈性彈簧力組成的，輪胎彈簧和所有阻尼器均可被認為是線彈性的，眾多學者[6,16-17]在研究車重多沖擊系數影響時，均采用的線彈性彈簧力為懸掛力，認為車重在合理取值范圍內，懸掛彈簧、輪胎彈簧及阻尼器均可被認為是線彈性的，即車體重量在合理范圍內調整時，懸掛參數是不改變的。相關標準DB61/T 916—2014《公路橋梁(梁式橋)荷載試驗技術規程》[23]規定，三軸載重車總重不宜大于38 t，且單軸重不大于16 t，參照相關規范并結合所選車型，本文選擇載重在25～38 t的車輛進行分析，通過改變表1中車體質量參數來實現調整車輛載重，懸掛參數不變。

表1 車輛模型參數Tab.1 Vehicle model parameters

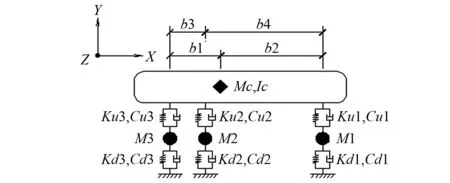
圖1 五自由度三軸平面車輛模型Fig.1 Five-degree-of-freedom three-axis planar vehicle model

圖1中，車體質量Mc有仰俯旋轉自由度α和豎向位移z，構架與輪對質量之和M1、M2、M3的豎向位移自由度z1、z2、z3，Ku、Cu為一系懸掛剛度、阻尼，Kd、Cd為二系懸掛剛度、阻尼。

根據達朗貝爾原理可得三軸平面車型振動方程：

(2)

式中：[Mv]、[Cv]、[Kv]分別為質量矩陣、阻尼矩陣、剛度矩陣；{Fbv}為輪胎與橋面接觸點處的瞬時耦合荷載向量；{Gv}為重力荷載向量。

1.3 橋梁模型

本文以標準跨徑的簡支小箱梁橋為研究對象，計算跨徑分為20 m、30 m、40 m，橋面凈寬11 m，橫向布置4片梁，20 m跨徑小箱梁橫斷面形式如圖2所示，運用ANSYS有限元程序建立空間梁格模型，如圖3所示。

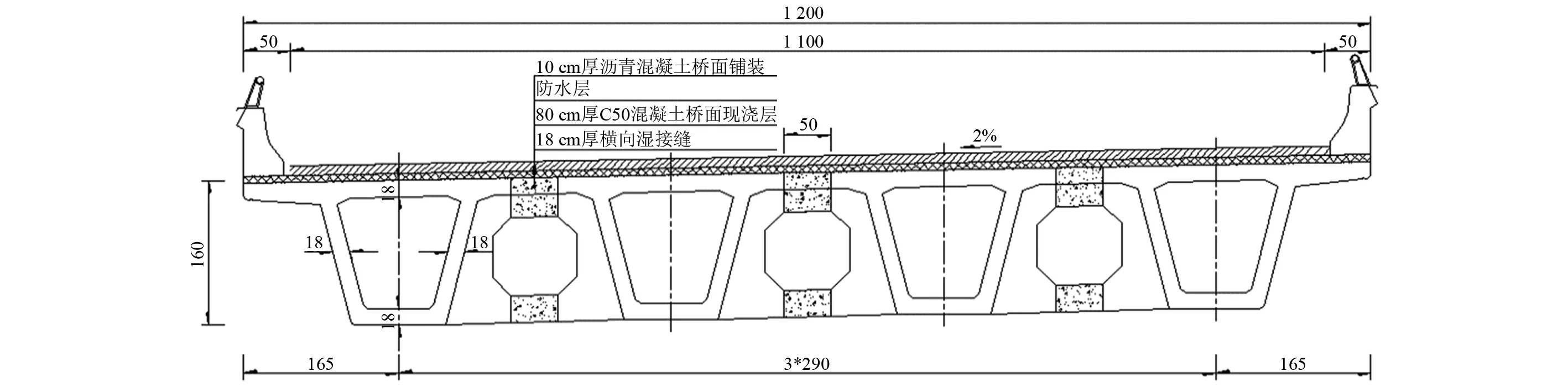
圖2 簡支小箱梁橋橫斷面圖(cm)Fig.2 Cross section of simply supported box girder bridge(cm)

圖3 簡支小箱梁橋模型示意圖Fig.3 Model diagram of simply supported box girder bridge

1.4 橋面平整度

橋面平整度是影響車橋耦合振動的重要因素，本文采用傅里葉變逆換法并參考GB7031—1986《車輛振動-路面平度表示方法》生成橋面平整度樣本。

傅里葉逆變換的平整度數值模擬計算模型如下式：

(3)

式中：xm為平整度的離散序列,Xk為離散傅里葉變換信號的模值；N為采樣點數。

由調查可知，我國橋面平整度大多處于A、B、C三個等級范圍內，因此以A、B、C三個等級的平整度作為研究參數，一組橋面平整度曲線如圖4所示。為減小不同橋面平整度樣本對計算結果的影響，使本文計算結果具有較好的代表性，每一個工況選取10組橋面平整度樣本計算動力響應，求10組樣本動力響應的平均值作為該工況計算結果。

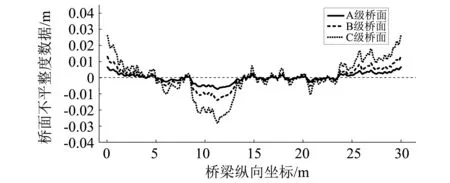
圖4 一組橋面平整度曲線Fig.4 A set of bridge deck flatness curves

2 準設計狀態下沖擊系數的分析

要正確評價沖擊系數，首先要采用與設計荷載等效的車輛荷載，進行準設計狀態下的沖擊系數研究。

2.1 分析方法及實例驗證

本文采用ANSYS的二次開發語言APDL對車橋耦合振動進行數值分析[24]，借助APDL語言實現車輛移動過程中對式(1)中{Fbv}的瞬時計算，將式(1)中{Gv}+{Fbv}荷載施加于各節點，并調用ANSYS的時程分析功能對每個子步計算，解出車橋之間的接觸力，進而計算時程響應。

為驗證本文程序的正確性，采用經典文獻[25]中的橋梁與車輛參數，將文獻中計算結果與本文程序計算結果進行對比，文獻中計算結果如圖5(a)所示，本文程序的計算結果如圖5(b)所示。對比分析可知，本文程序計算結果無論是數值大小還是變化趨勢均與參考文獻吻合。通過將本程序有限元計算值與實測值進行對比發現吻合度較好，驗證了車橋分析方法及本文數值計算結果的準確性。

圖5 不同速度移動荷載作用下橋梁跨中的位移響應Fig.5 Displacement response of bridge midspan under moving loads at different speed

2.2 準設計狀態的概念

荷載效應等效比計算式：

(4)

式中：η為荷載效應等效比；Ss為靜載作用下，某一加載試驗項目對應的加載控制截面內力或位移的最大計算效應值；S為控制荷載作用下控制截面內力或位移的最不利效應計算值(不計沖擊效應)；控制荷載為進行荷載試驗所確定的荷載，可用來確定荷載試驗效率，這里指設計荷載。

2.3 準設計狀態的車輛布載

由簡支小箱梁橋橫斷面的對稱性，選擇1#、2#主梁分析。車輛布載參照規范，橫向車間距為1.3 m，縱向車間距為5 m，縱向車輛首尾銜接。將車輛重量分配在車輛各軸，通過將車輛各軸在簡支梁各片梁跨中位置處的縱向位移影響線上加載，得到在簡支梁跨中位置產生最大位移效應時的各軸的縱向位置，從而確定準設計狀態車輛加載位置，車輛布載方式如圖6所示。

計算各跨徑簡支小箱梁橋在公路Ⅰ級設計汽車荷載(不計沖擊系數)作用下跨中控制截面的撓度效應值，然后將車輛按照圖6的布載方式加載，調整車輛載重，并按式(4)計算各跨徑橋梁跨中1#、2#主梁撓度效應等效比，使其等于或接近1，達到準設計狀態。計算結果見表2。

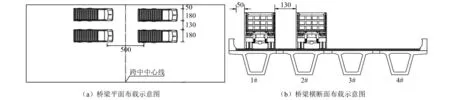
圖6 車輛布載方式(cm)Fig.6 Vehicle loading mode(cm)

表2 簡支小箱梁橋跨中撓度效應等效計算結果Tab.2 Equivalent calculation results of mid span bending moment effect of simply supported box girder bridge

參考JTG/TJ21-01—2015《公路橋梁荷載試驗規程》[21]，當荷載效應等效比介于0.95～1.05之間，則認為車輛荷載效應與設計荷載效應等效，此時稱為準設計狀態。

2.4 準設計狀態沖擊系數分析

結合我國橋面實際情況，選取三個行駛速度20 km/h、60 km/h、100 km/h表征低、中、高速行駛狀態，考慮A、B、C三個橋面平整度等級，同時選取十組橋面平整度樣本對20 m、30 m、40 m跨徑簡支小箱梁橋進行準設計狀態下車橋耦合振動分析，取10組樣本動力響應的平均值作為計算結果，車輛橫斷面布載形式見圖6。

任一跨徑橋梁的分析工況排列組合共計18個，對各工況的車橋耦合振動問題進行求解，得到撓度時程曲線，部分40 m跨徑小箱梁在B級橋面平整度下的撓度時程曲線見圖7。

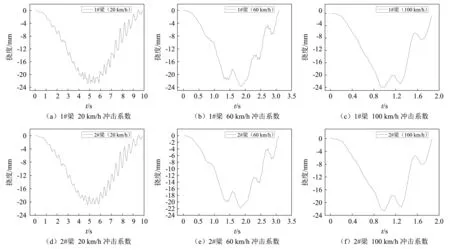
圖7 40 m跨徑小箱梁撓度時程曲線Fig.7 Deflection time-history curve of 40 m span box girder

為了直觀分析簡支小箱梁橋各主梁在準設計狀態下的沖擊系數，定義沖擊系數計算值超過規范值的工況數與總的工況數的比值為超規范工況百分比，按照15規范計算沖擊系數的規范值，將簡支小箱梁橋所有工況的沖擊系數計算結果進行統計分析后，匯總于表3。

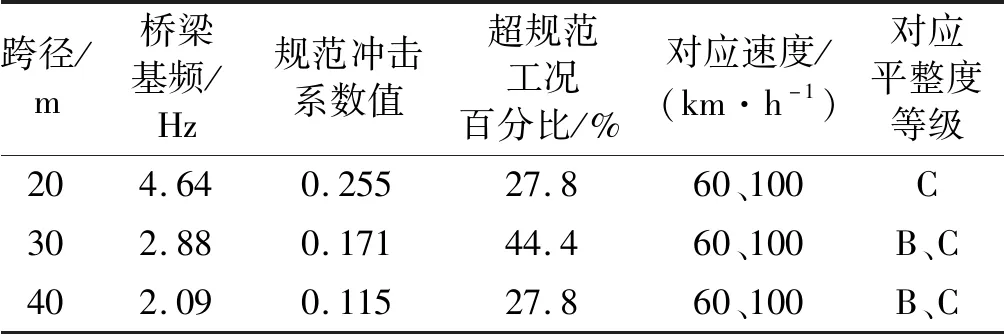
表3 簡支小箱梁橋撓度沖擊系數超工況統計Tab.3 Working condition statistics of deflection impact coefficient of simply supported box girder bridge

由表3可得，橋梁跨徑為30 m時超規范工況百分比最大。分析其原因，通過ANSYS有限元程序建立了如圖1所示的車輛系統模型，調整車輛載重，進行模態分析，采用LANB法提取相應的車輛豎向自振基頻，30 m跨徑橋梁對應加載車的車輛系統的豎向自振基頻為2.77 Hz，30 m跨徑小箱梁的基頻為2.88 Hz，30 m跨徑小箱梁的基頻與車輛懸掛系統的豎向自振基頻較為接近，使系統振幅增大，造成30 m跨徑小箱梁的沖擊系數超規范工況百分比最大。

速度對沖擊系數的影響規律不明顯，各跨徑小箱梁超規范工況均出現在中、高速。超規范的工況均發生在B、C級平整度橋面，可見橋面平整度對沖擊系數影響非常大。對于各跨徑簡支小箱梁橋，按規范取值的沖擊系數與偏不安全，但在橋面狀況良好和低速行駛時安全性較高。

3 動載試驗荷載效率下沖擊系數分析

通過調研大量動載試驗工程實例，發現在相關規范[21,23]對加載效率無明確規定的前提下，為測試簡便與保證試驗安全，實際簡支梁橋動載試驗時，通常僅采用單輛25～38 t的三軸載重車進行加載，此時動載試驗荷載效率較小。

通過改變車輛的載重為25～38 t來模擬動載試驗荷載效率的變化，選擇20 km/h、60 km/h、100 km/h表征低、中、高速行駛，考慮A、B、C三個橋面平整度等級，并取10組平整度樣本計算20 m、30 m、40 m跨徑簡支小箱梁橋在不同動載試驗荷載效率下的沖擊系數，來分析動載試驗荷載效率對橋梁沖擊系數的影響，并對輕荷載作用下的沖擊系數進行修正分析。

3.1 動載試驗荷載效率計算

(1)動載試驗荷載效率計算式：

(5)

式中：ηd為動載試驗荷載效率；Sd為動載試驗荷載作用下控制截面的最大內力或變形；S為控制荷載作用下控制截面的最大內力或變形(不計沖擊)；控制荷載為進行荷載試驗所確定的荷載，可用來確定荷載試驗效率，這里指設計荷載。

(2)車輛荷載作用方式

為使研究模擬過程貼切實際，車輛行駛車道寬度取值3.5 m，且車輛始終行駛在車道中間。以1#梁作為研究對象，由于車道寬度3.5 m，輪距為1.8 m，車輛橫向布置在距護欄0.85 m處；以2#梁作為研究對象，車輛橫向布置在2#梁的中心線處，具體布載方式如圖8所示。

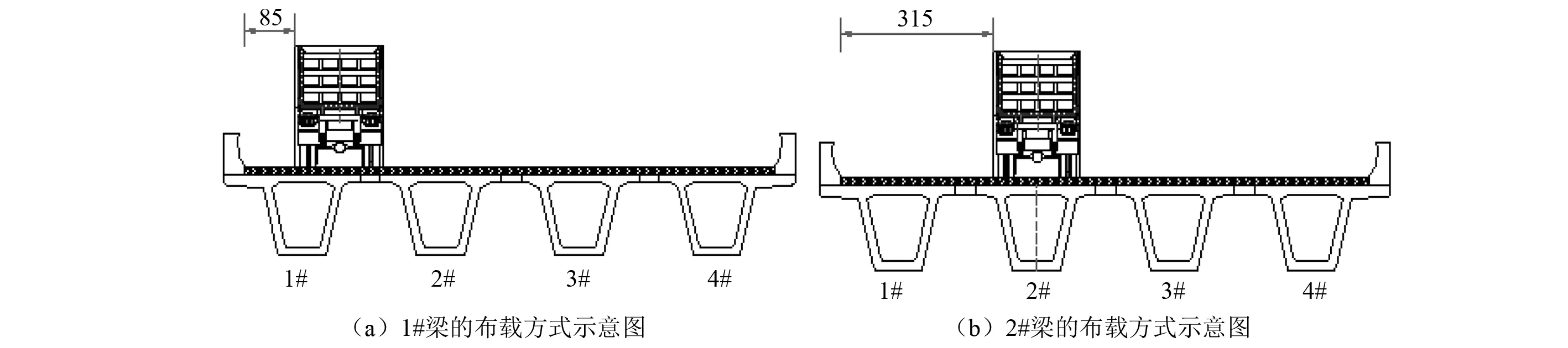
圖8 簡支小箱梁橋單輛車橫向布載示意圖(cm)Fig.8 Schematic diagram of lateral load of single vehicle on simply supported box girder bridge(cm)

(3)動載試驗荷載效率計算

按圖8的布載方式將單輛車荷載加載在橋梁跨中位置縱向位移影響線的最不利位置處，并通過改變三軸車輛的載重為25 t、30 t、35 t、38 t，來模擬動載試驗荷載效率的改變。按式(5)計算各跨徑簡支小箱梁橋1#、2#主梁的跨中撓度效應的動載試驗荷載效率，計算結果見表4所示。

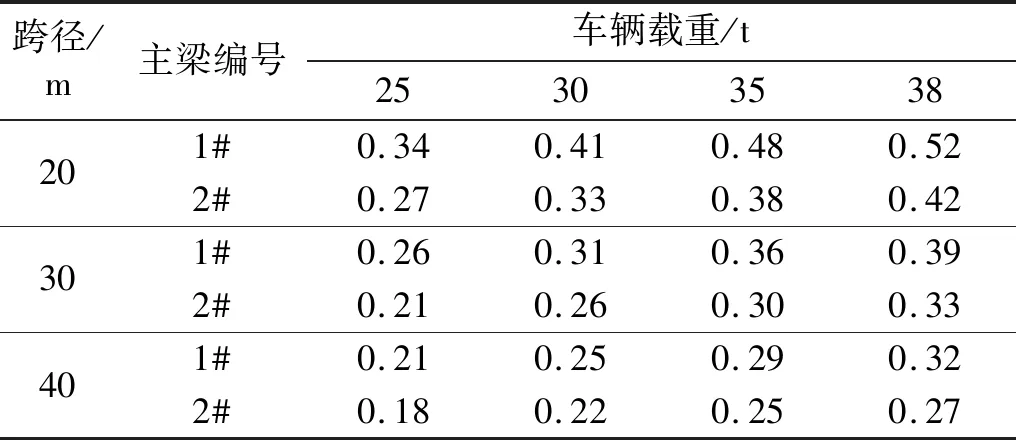
表4 簡支小箱梁橋跨中撓度效應動載試驗荷載效率Tab.4 Effect of deflection in midspan of simply supported box girder bridge load efficiency of dynamic load test

3.2 動載試驗荷載效率對沖擊系數的影響

對20 m、30 m、40 m跨徑簡支小箱梁橋進行車橋耦合振動分析，三軸車輛載重以25 t、30 t、35 t、38 t變化來模擬動載試驗荷載效率的改變。考慮A、B、C三個橋面平整度等級，并選擇10組平整度樣本，同時選取三個行駛速度20 km/h、60 km/h、100 km/h表征低、中、高速行駛。

對各工況進行車橋耦合振動求解，得到簡支小箱梁橋的撓度時程曲線，根據時程曲線計算沖擊系數，將1#、2#梁的撓度沖擊系數按不同速度繪制于圖9～圖11，分析沖擊系數隨動載試驗荷載效率改變而變化的規律。

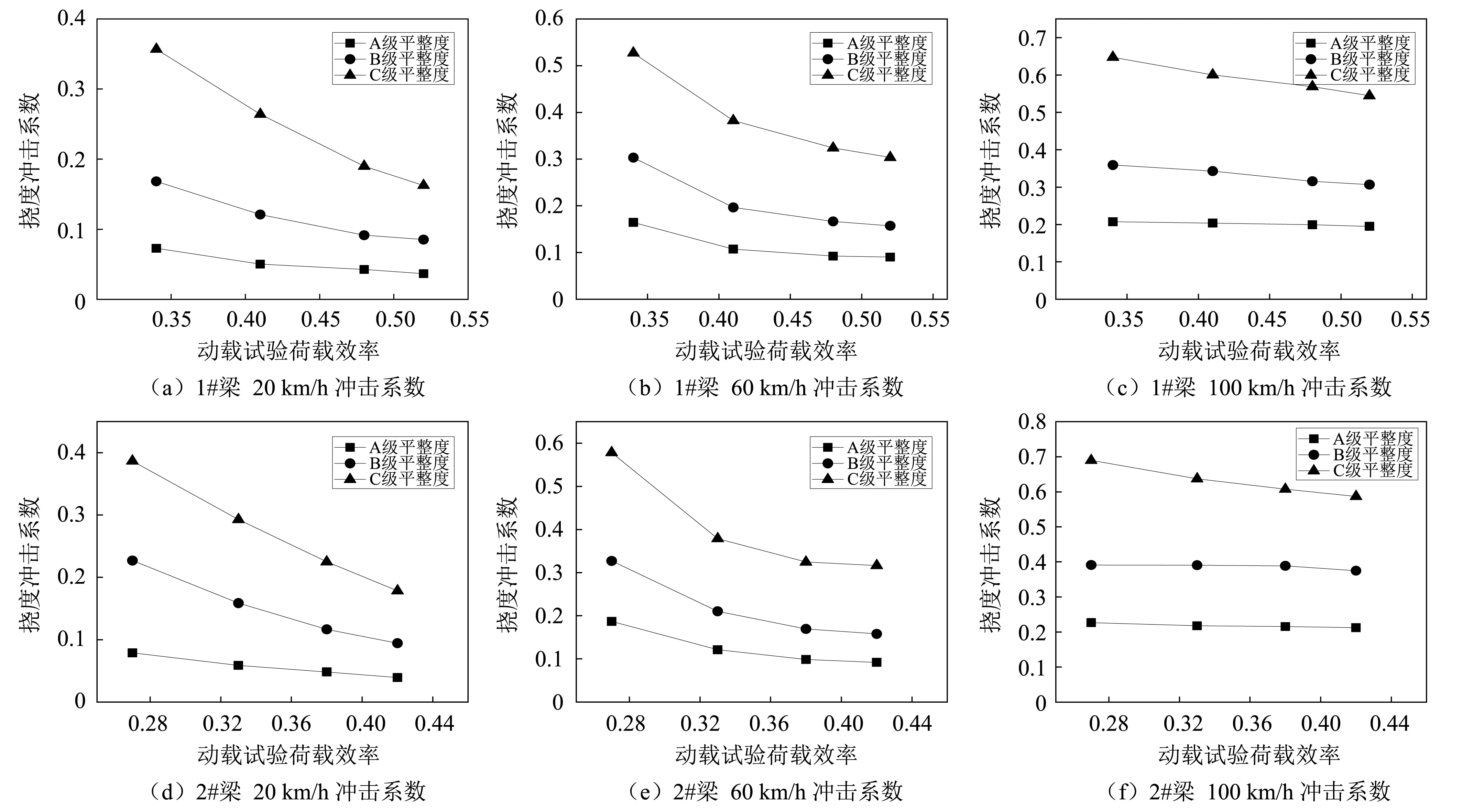
圖9 20 m跨徑簡支小箱梁撓度沖擊系數Fig.9 Deflection impact factor of 20 m span simply supported box girder

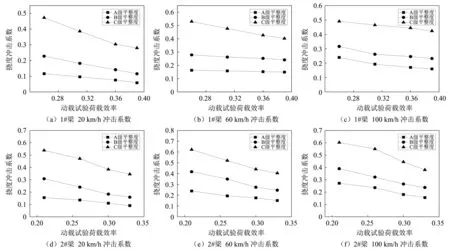
圖10 30 m跨徑簡支小箱梁撓度沖擊系數Fig.10 Deflection impact factor of 30 m span simply supported box girder

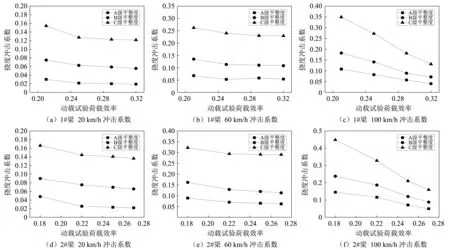
圖11 40 m跨徑簡支小箱梁橋沖擊系數Fig.11 Deflection impact factor of 40 m span simply supported box girder

由圖9～圖11分析可得，在單輛車荷載作用下，基于動載試驗荷載效率，各跨徑簡支小箱梁1#、2#的撓度沖擊系數有如下特征：

(1)總體來講，1#、2#梁的撓度沖擊系數隨著動載試驗荷載效率的增大而逐漸減小，且遞減速率逐漸變小，說明輕荷載容易產生更大的沖擊系數。

(2)隨著橋面平整度狀況變差，各片梁撓度沖擊系數隨動載試驗荷載效率變化的趨勢變陡，隨著動載試驗荷載效率的增大，各平整度下的趨勢線間的距離減小，當動載試驗荷載效率最小時，20 m跨徑、30 m跨徑、40 m跨徑小箱梁A級與C級平整度下的沖擊系數差值最大分別為0.460、0.383、0.300，當動載試驗荷載效率最大時，差值最大分別為0.362、0.264、0.220。說明隨著橋面平整度越差，沖擊系數越大，當動載試驗荷載效率增大時，沖擊系數的增大幅度減小。

(3)相同工況下的1#、2#梁，C級平整度下，當動載試驗荷載效率最小時，20 m、30 m、40 m跨徑的簡支小箱梁兩者沖擊系數最大差值分別為0.050、0.112、0.100；當動載試驗荷載效率最大時，最大差值分別為0.042、0.065、0.028。A級平整度下，當動載試驗荷載效率最小時，各跨徑簡支小箱梁兩片梁沖擊系數最大差值分別為0.022、0.076、0.037；當動載試驗荷載效率最大時，最大差值分別為0.017、0.032、0.010。說明隨著動載試驗荷載效率增大，相同工況兩片梁的撓度沖擊系數差值減小，且橋面平整度等級越高，沖擊系數差值越小。

(4)速度對撓度沖擊系數影響較大，但無明顯規律。高速狀態下，撓度沖擊系數與動載試驗荷載效率有呈線性變化的趨勢。

3.3 簡支梁橋沖擊系數修正分析

3.3.1 修正系數定義分析

根據YC4-4—1978《大跨徑混凝土橋梁的試驗方法》中規定：

(δmax-1)ηdyn≤δ-1

(6)

式中：δmax為實測動力放大系數；ηdyn為動載試驗荷載效率；δ為設計取用的動力放大系數。

該規范規定輕荷載下沖擊系數取值采用動載荷載效率進行修正，但是根據本文上述研究，準設計狀態的沖擊系數與輕荷載的沖擊系數之間的關系并不明確，其與平整度等級、速度、跨徑等有關系，以此方法修正沖擊系數的合理性有待商榷。

依據該規范并結合本文上述研究，且考慮對實際工程的實用原則，對輕荷載下沖擊系數進行修正，建立單輛車作用下沖擊系數與準設計狀態下沖擊系數的關系。引入修正參數ζ，ζ為考慮平整度等級、速度、跨徑等因素對沖擊系數影響的待定常值。基于此，提出能夠便于工程應用的單輛車試驗沖擊系數的修正系數ηdζ。

(7)

式中：us為準設計狀態下的沖擊系數；uq為與準設計狀態相應的單輛車的沖擊系數；ηd為與準設計狀態相應的單輛車的動載試驗荷載效率；ζ為待定常值。

3.3.2 修正系數計算分析

橋梁動載試驗通常是輕荷載在低速狀態下進行，且B級平整度橋面最為常見。因此選擇速度20～60 km/h，平整度等級為B級的工況，通過改變三軸載重車的載重為25 t、30 t、35 t、38 t，來模擬動載試驗荷載效率的改變。選擇10組平整度樣本對準設計狀態和單輛車作用的車橋耦合振動問題進行求解，得到撓度時程曲線，計算各工況的沖擊系數后按式(7)計算各跨徑ζ值。統計計算結果后，發現各跨徑橋梁不同動載試驗荷載效率下的ζ值在同一速度下較接近，對各跨徑同一速度下的ζ值進行數據處理，剔除個別離散性較大的值后，取均值作為考慮平整度等級、速度、跨徑等影響因素的修正參數ζ。

簡支小箱梁橋在單輛試驗車作用下的沖擊系數修正系數為ηdζ，本文給出B級平整度下考慮不同影響因素的ζ值，見表5。

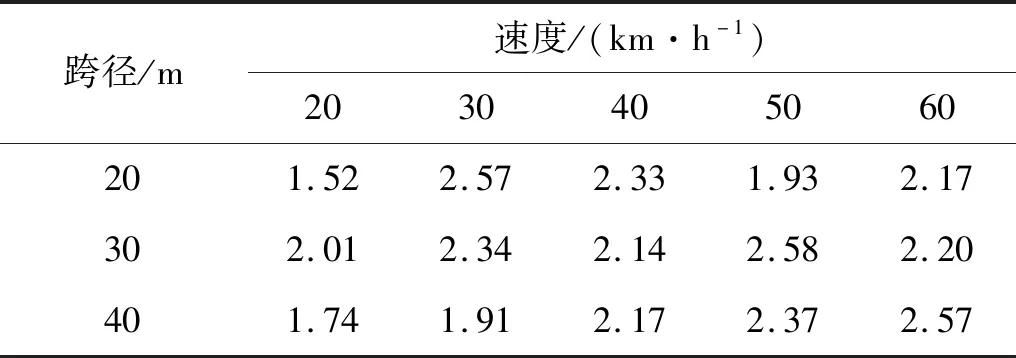
表5 各跨徑簡支小箱梁橋ζ平均值Tab.5 ζ average value of each span simply supported box girder bridge

由大量數據進行統計分析后得出的修正參數ζ，并結合動載試驗荷載效率ηd，可得修正系數ηdζ。使用修正系數對單輛車作用下的輕荷載沖擊系數進行修正，得到準設計狀態下的沖擊系數，即等效設計荷載作用下的沖擊系數，便于對橋梁動載試驗中輕荷載作用下的沖擊系數進行評價。

4 結 論

本文以標準跨徑的簡支小箱梁橋為研究對象，采用五自由度三軸平面車輛模型，考慮了平整度、速度、跨徑等影響因素，將設計車道荷載還原為等效的車輛荷載，進行了準設計狀態下沖擊系數的分析；分析了基于動載試驗荷載效率的撓度沖擊系數的變化規律，并提出了單輛車輕荷載下試驗沖擊系數的修正方法，建立了簡支小箱梁橋輕荷載沖擊系數與準設計狀態沖擊系數的關系。得出以下主要結論：

(1)將設計荷載的車道荷載等效還原為多輛重車荷載，進行準設計狀態下的車橋耦合振動分析，結果表明按15橋規取值的沖擊系數并不安全，但在橋面狀況良好和低速行駛時安全性較高。

(2)整體來看，簡支小箱梁橋的沖擊系數隨動載試驗荷載效率的增大而逐漸減小，且遞減速率逐漸減小。說明輕荷載容易產生更大的沖擊系數，通過輕荷載所得的沖擊系數直接與規范值對比評價并沒有實際意義。

(3)橋面平整度狀況較好時，沖擊系數隨動載試驗荷載效率增大略有降低，隨著動載試驗荷載效率增大各片主梁的沖擊系數相差微小或相等；橋面平整度等級較低時，沖擊系數迅速增大，但動載試驗荷載效率的增大會減緩其增大速率。

(4)輕荷載容易產生更大的沖擊系數，因此提出了基于動載試驗荷載效率的單輛車作用下的沖擊系數修正方法，提出了修正系數ηdζ，此修正系數與平整度等級、跨徑和車速等有關，建立了單輛車作用下沖擊系數與準設計狀態下沖擊系數的關系，可為公路簡支梁橋沖擊系數的修正及評價提供參考。