基于全箭振型數據的大型捆綁火箭模態篩選與對齊方法

胡明明，譚述君,2，周如好，何 驍

(1.大連理工大學 航空航天學院，遼寧 大連 116023；2.遼寧省空天飛行器前沿技術重點實驗室，遼寧 大連 116023；3.上海航天控制技術研究所，上海 201109)

隨著科技的不斷發展，空間技術是每一個大國爭相發展的技術。而運載火箭是人類進入空間的最主要手段[1]。考察國內外同類捆綁火箭,如大力神-ⅢC[2]、土星V[3]、航天飛機[4]、阿里安-4[5],CZ-2E[6]、長征五號[7]等，可以看出隨著火箭的大型化、長助推化發展，捆綁火箭彎、扭、縱耦合嚴重，形成十分復雜的模態族[8]。同時，運載火箭在飛行過程中隨著燃料的消耗，彈性模態也不斷變化，甚至會出現模態跳躍和消失的現象[9]，從而給運載火箭動力學建模和控制帶來極大的困難。因此提出大型捆綁火箭有效的模態篩選和對齊方法是非常必要的。

常用的模態篩選方法有模態有效質量法[10]和能量分數法[11]等等。Chung等[11]還提出了模態有效質量和能量分數相結合的方法，以便將整體和局部模態都包括在內。模態百分比法[12]則是在所考慮的激勵頻率范圍內量化模態相對重要性的方法[13]。Mercer等[14]對以上方法作了對比評估，并分析了其工程價值。傳統的運載火箭模態篩選方法一般僅利用頭部單點的模態數據進行模態篩選。運載火箭則提出了平方根位移法}，該方法易于受到特定位置或特定點選取的影響。對于捆綁火箭的復雜模態，單純利用某一點或特定位置的振型數據已很難區分，因此有必要利用全箭振型數據進行模態篩選。吳勝寶等[16]公布了一種大型液體捆綁火箭復雜模態辨識方法。王勇[17]提出一種基于火箭芯級振型數據的模態篩選方法，提高了模態篩選的正確性，然而對某些助推器局部模態未能很好的篩選出來，并且該方法在歸一化操作中沒有區分振型數據的橫向位移和角位移量綱的不同。

傳統的模態對齊方法一般是按照頻率的大小進行對齊，如鄧舞燕[18]提出的模態對齊思路，然而從本質上來說模態對齊應該是模態形狀的對齊，而模態形狀和模態頻率之間并沒有必然的聯系。Allemang等[19]提出了一種基于模態置信度準則(MAC)的模態快速自動排列技術。該方法使用了模態振型數據，提高了模態對齊的準確性，但是模態置信度準則只是按照相似度值來對齊，可能導致不同的模態類型的對齊，并且還可能導致出現某一階次同時和好幾個階次對齊的問題。

本文充分利用芯級和助推器的振型數據，改進了模態振型數據的歸一化方式，提出了彎曲模態、扭轉模態、縱振模態及局部模態等的模態篩選系數公式。并改進了基于振型數據的模態置信度準則的對齊方法，從而實現大型捆綁運載火箭的模態篩選和對齊。最后，在某型號運載火箭時變動力學模型上進行了仿真驗證。

1 傳統的火箭模態篩選方法

傳統火箭長細比較小，模態類型較為簡單，并且縱橫扭耦合不嚴重，因此一般通過頭部點(一般是火箭的理論尖點)振型數據來判斷模態類型。例如某工業部門進行某構型火箭姿控系統設計時曾使用一種單點法的模態篩選方法[17]。該方法首先取該時刻各模態頭部點(一般是火箭的理論尖點)振型數據的6個分量值[UXUYUZRXRYRZ]T，按照最大值歸一化。然后計算模態分量UY/UZ，RX，UX的值進行模態篩選，結果如下：

(1)UY/UZ=1時，為45°(或-13.5° )方向的彎曲模態。

(2)UY/UZ=-1時，為45°(或135° )方向的彎曲模態。

(3)RX=1時，為扭轉模態。

(4)UX=1時，為局部模態。

該技術經過仿真驗證，對于傳統火箭具有很好的可行性和工程價值。但其僅利用頭部點振型數據對模態進行篩選，沒有充分利用模態振型數據，因此，對大型捆綁火箭的復雜模態形狀的判別不夠準確，本文將發展基于全箭振型數據的模態篩選方法。

2 基于全箭振型數據的模態篩選方法

大型捆綁運載火箭長細比較大，縱橫扭耦合嚴重，導致其模態十分復雜。并且火箭的模態類型是由火箭整體模態振型數據來體現的，僅僅使用模態頭部點是不夠的。本節在王勇的基礎上，首先充分利用芯級和助推器振型數據提出了模態類型的精細化定義，然后對模態振型數據歸一化方式和彎曲、扭轉、縱振的篩選系數公式做出了改進，從而建立了適應大型捆綁火箭的新的模態篩選方法。

2.1 模態類型的定義

對于大型捆綁火箭，助推器的長細比也越來越大，導致助推器的模態振型成為構成整個箭體模態振型的重要組成部分，不宜忽略。因此，利用芯級和助推器振型數據分別對芯級和助推器進行模態篩選，得到的模態篩選結果如下表 1所示。這樣的分類可以很好的將捆綁火箭的整體振型特征和耦合模態描述出來。其中XJ表示芯級,ZT表示助推器，XJ彎ZT彎表示芯級是彎曲模態且助推器是彎曲模態，以此類比。

表1 模態類型組合Tab.1 Combination of modal types

2.2 振型數據歸一化處理

分別對芯級和助推器進行振型數據歸一化處理，令其全部站點x，y，z的歸一化位移平方和為：

(1)

令全部站點y橫向的歸一化位移平方和為：

(2)

令全部站點x，y，z的歸一化轉角平方和為：

(3)

令全部站點x的歸一化轉角平方和為：

(4)

同理Siz、Six、Siry和Sirz也是類似定義。

2.3 模態類型的表征

對于彎曲模態來說，其y方向和z方向的模態位移較大，因此彎曲模態的表征系數如下：

(5)

對于縱振模態來說，其x方向的模態位移較大，故縱振模態的表征系數如下：

(6)

而對于扭轉模態來說，其繞x方向的轉角位移較大，由此，扭轉模態的篩選公式使用轉角數據。扭轉模態表征系數如下：

(7)

同時，對于彎曲模態來說，其繞y和z軸的轉角位移較大，因此也可以采用轉角數據進行檢驗，公式如下：

(8)

此時，若為彎曲模態，則由轉角計算出的ηr也是接近于1。

對于彎曲模態，進一步可以將其分為俯仰和偏航。其中俯仰或偏航模態類型表征系數計算公式如下：

(9)

其中當ξ>1時，為俯仰模態，反之為偏航模態。

根據計算出的模態類型表征系數，找出最大值，那么該最大值所屬的模態類型即為當前階次的模態類型。

最后對于局部模態的判斷，引入一個比重系數λ，定義如下：

λ1是芯級比重的系數，由芯級所有數據平方和平均后，再開根號。n1為芯級站點個數，Si,xj是芯級所有站點位移平方加和，表達式為

(10)

(11)

λ2是助推器比重系數，Si,zt是助推器所有站點位移平方加和，其定義也是類似Si,xj，n2是助推器個數，同理：

(12)

(13)

當λ≥100%時，表示芯級變形為主；反之助推器變形為主。此時助推器的數據，按照一個助推器或者多個，對于芯級比重判別幾乎沒有影響。

3 不同秒點的模態對齊方法

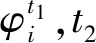
(14)

MAC值介于之間，MAC值越大，模態越相似。模態置信度與模態本身幅值大小無關，只與模態本身形狀有關，因此不受模態歸一化方式的影響。

然而，由于大型捆綁運載火箭模態振型的復雜性，僅利用模態置信度準則可能導致不同的模態類型進行了對齊，并且還有可能導致某一階次重復性對齊，使得模態數據難以對齊。對此，本文先進行模態篩選，然后結合模態篩選結果，利用模態置信度準則完成不同秒點的對齊。具體步驟如下：①對所有秒點進行模態篩選，按模態類型進行分類；②對于每一類型模態的集合，分別利用MAC準則去下一個秒點的對應類型的模態集合里進行對齊；③將已對齊的階次進行跳過，得到該模態類型的所有對齊的結果；④將遺漏的階次去下一個秒點剩下的所有階次里進行對齊，直到所有的階次都對齊為止。例如第0 s的俯仰彎曲模態類型，先從下一個秒點的俯仰彎曲模態集里找到與其對齊的階次，最后將第0 s遺漏的未對齊的階次按照置信度準則從下一個秒點剩下的階次中找對齊即可。

4 仿真驗證

采用本文提出的模態篩選、對齊方法，利用某型號大型捆綁火箭模態振型數據，完成了該火箭動力學模型的模態篩選和對齊，并與模態振型圖進行對比，來驗證本文方法的有效性。進一步將模態篩選和對齊結果在某型號捆綁火箭姿態控制系統模型上進行了仿真驗證。

4.1 模態篩選方法的驗證

使用某型號捆綁火箭的模態振型數據進行模態篩選，以該火箭第5 s的振型數據為例，其模態篩選結果如表 2所示。表中第6列為綜合后的模態篩選結果，分別為芯級變形為主的整體俯仰彎曲、偏航彎曲、扭轉和縱振模態，以及助推變形為主的局部模態。同時給出了芯級、助推器模態類型及芯級占全箭比重等信息。表中篩選的俯仰彎曲模態和偏航彎曲模態的頻率相互對應，也從側面驗證了篩選結果的正確性。

為了驗證表 2的篩選結果，將第5 s的前30階模態振型圖畫出。圖 1分別給出了第1、2、6、12、22、30階的振型圖，可以看出它們分別是偏航彎曲、俯仰彎曲、局部助推彎曲、扭轉、縱振和俯仰彎曲模態，這與表 2篩選結果一致，驗證了本文篩選方法的正確性。值得說明的是，圖 1中第30階的俯仰彎曲模態體現的是火箭頭部局部變形，這一點本文方法并沒有刻畫出來。

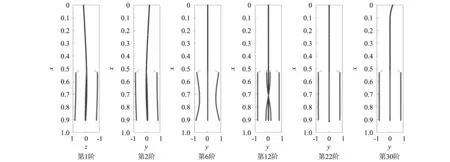
圖1 部分階次振型圖Fig.1 Partial order mode shape diagram

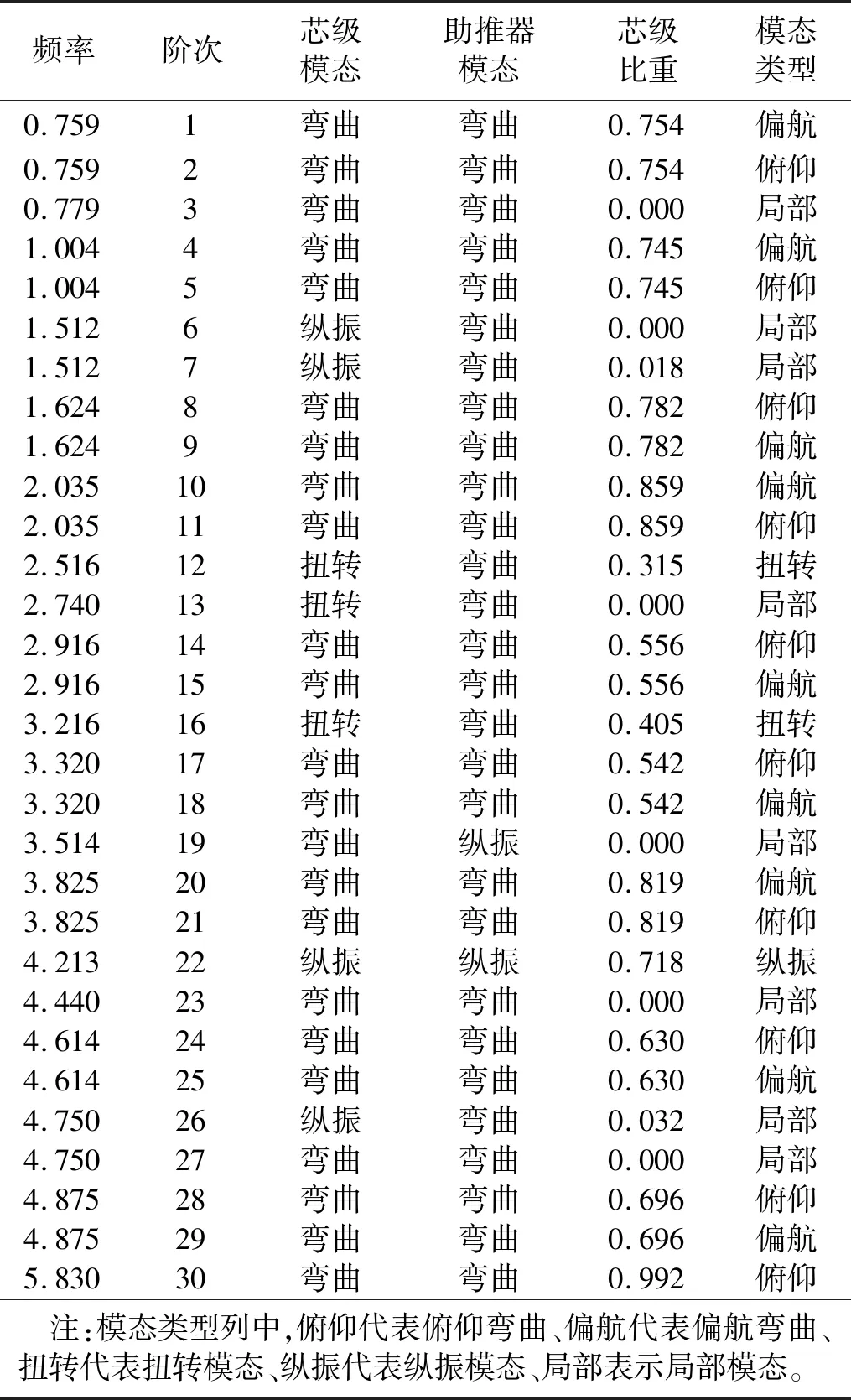
表2 第5 s時刻前30階模態篩選結果表Tab.2 The first 30 orders results of modal selection at the 5th second

4.2 模態對齊方法的驗證

將第0 s的模態篩選結果，按照彎曲(俯仰彎曲和偏航彎曲)、扭轉、縱振、局部模態依次排列，然后利用本文方法對后續秒點進行模態對齊。限于篇幅，表 3列出了彎曲(5階)、扭轉(2階)、縱振(1階)、局部模態(2階)的對齊結果。從表中給出模態類型可以看出第0 s、第5 s、第35 s的階次完全對齊，第125 s的對齊結果中只有第20階(模態類型是局部模態)與前面的秒點階次(模態類型是俯仰彎曲)沒有對齊，產生偏差的原因可能是由于時間間隔過大，導致沒有十分匹配的階次與其相對應，這也提示在模態對齊時秒點間隔不能太大。

為驗證表 3的對齊結果，將不同秒點對齊結果的振型圖畫出。限于篇幅，僅給出第0 s的第1階的對齊結果圖，如圖2所示。通過振型圖可以看出，不同秒點的振型圖非常接近，對齊結果正確。

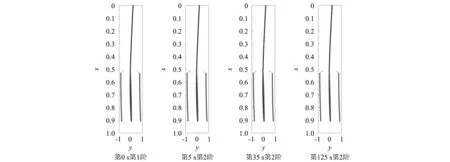
圖2 第0 s的第1階的對齊結果圖Fig.2 Alignment result of the 1st order of the 0th second

表3 4個秒點的模態對齊結果表Tab.3 4 seconds modal alignment result table

4.3 姿控系統模型的仿真驗證

運載火箭在飛行過程中的燃料消耗導致其模型是時變的，不同秒點的模態振型變化較大，同時隨著火箭柔性的增加，仿真模型中需要保留更高階的模態。如果模態篩選、對齊出現問題，將會導致仿真結果不合理、甚至發散終止。因此本文利用上面對該火箭的模態篩選、對齊結果，建立運載火箭的時變剛-彈姿態動力學模型，在專業仿真平臺進行姿控系統的仿真，驗證本文模態篩選、對齊方法的正確性。圖3～圖4給出了偏航通道姿態角和姿態角速度的響應曲線。可以看出，在運載火箭的整個飛行段中，雖然模型是時變的，干擾也是時變的，但是姿態角偏差響應曲線都在1°范圍之內，說明所設計的控制系統是穩定的。在60 s和80 s處出現的明顯波動，則是因為此處是大風區受較大的切變風干擾。圖5～圖6給出了對姿態穩定性影響較大的前兩階彈性振動模態的響應曲線，可以看出全箭彈性模態的波動曲線與姿態響應是一致的。上述仿真曲線與傳統上采用手動、經驗方法進行模態篩選和對齊得到的仿真模型的仿真曲線是一致的，驗證了本文提出的模態篩選、對齊方法的正確性。

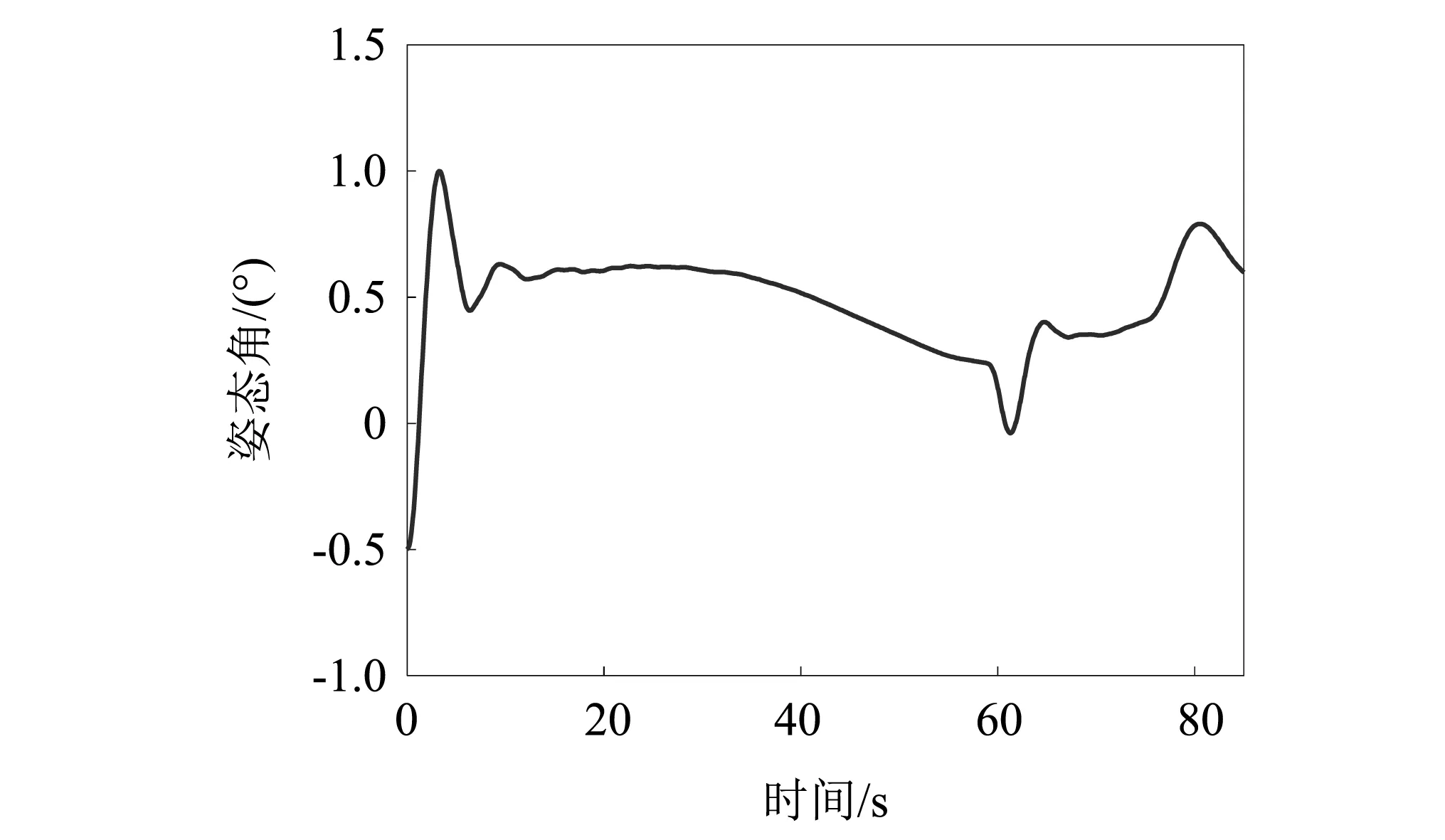
圖3 偏航姿態角曲線 Fig.3 The yaw attitude angle curve

圖4 偏航姿態角速度曲線Fig.4 Yaw attitude angular velocity curve

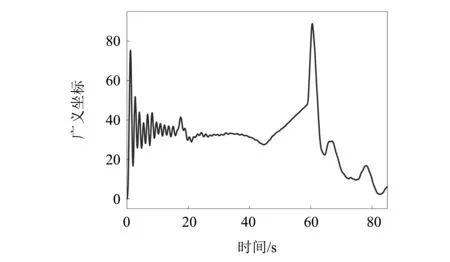
圖5 全箭一階彈性模態Fig.5 Full Rocket First Order Elastic Mode

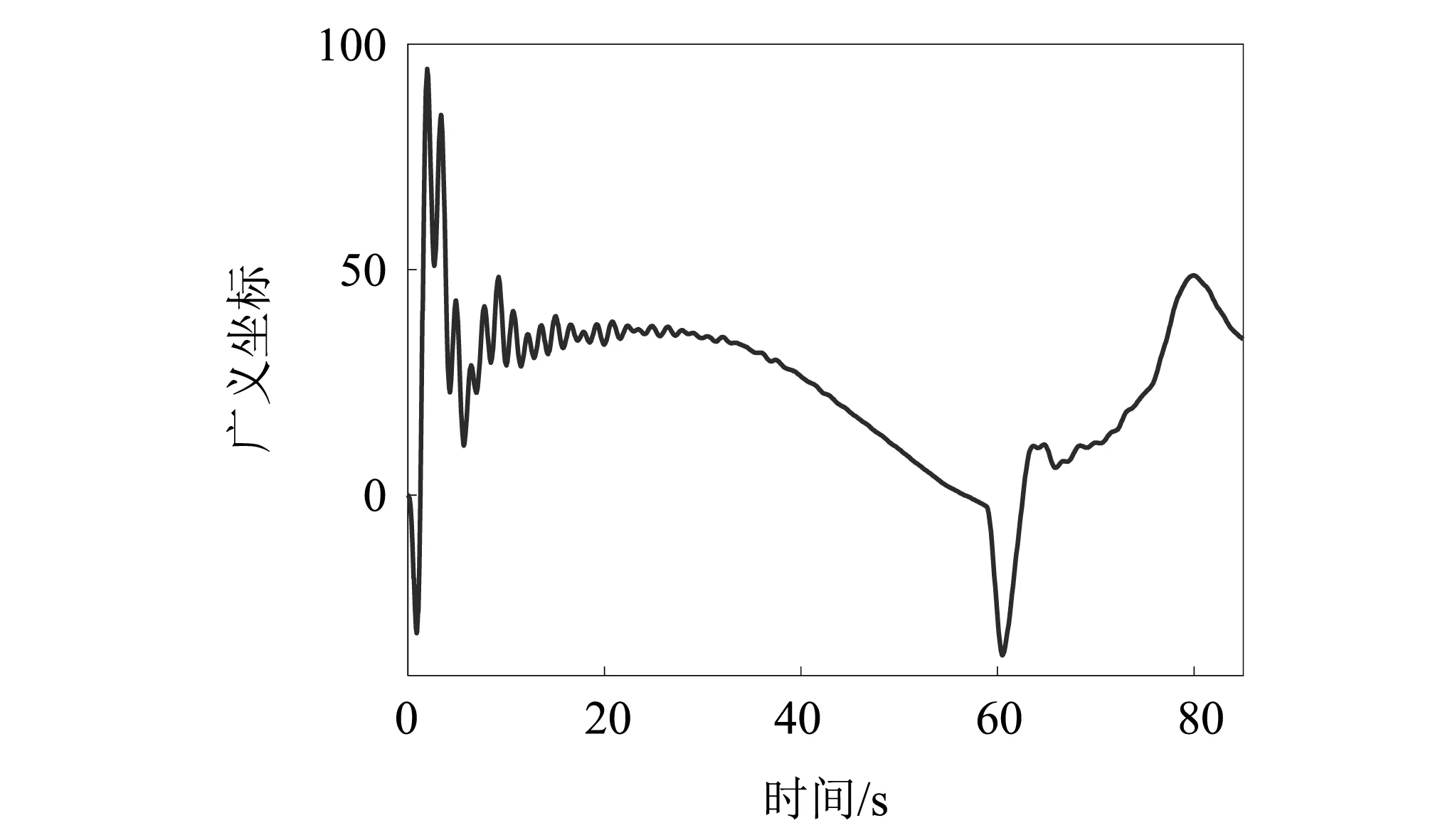
圖6 全箭二階彈性模態Fig.6 Full Rocket Second Order Elastic Mode

5 結 論

本文利用全箭振型數據提出了一種大型捆綁火箭的模態篩選和對齊方法，通過對芯級和助推器單獨進行模態篩選，給出了更準確的模態分類，并且定義了一個判別局部模態的系數，將以助推器為主的局部模態很好的篩選了出來。后續通過模態對齊和仿真驗證，得到了合理的仿真結果，進一步驗證了模態篩選和對齊的準確性，有效的解決了大型捆綁火箭模態復雜帶來的建模問題，為后續的復雜動力學仿真和姿態控制系統設計奠定了基礎。