新型覆土波紋鋼板-混凝土組合橋設計計算模型探討

劉 瑞，金浩然，孟根喜，劉保東，張繼磊

（1.內蒙古交通設計研究院有限責任公司，內蒙古 呼和浩特 010010；2.呼和浩特市公路勘察設計院；3.北京交通大學，北京 100089）

1 引言

近年來，重載交通、高填方、大跨度等新工況的出現對覆土波紋鋼板橋涵結構提出更高的要求，開發各種加強形式的波紋鋼板橋涵成為業界關心的重要課題之一。最直觀的解決方案即不斷加大波紋鋼板的波長和波高，國外已嘗試采用500mm×237mm波形[1]，如圖1所示。但當超過一定限度后，一味增加波高和板厚將導致結構經濟性變差。另一種可行的解決方案則是通過在波紋鋼板臺背澆筑混凝土，通過鋼-混組合截面協同承載提高主體結構正截面承載能力和穩定性。

圖1 不同波紋鋼板波形對比

波紋鋼板外覆混凝土一般用于修建開口式拱橋，該橋型為一種新型的組合橋型，主體結構為波紋鋼板-混凝土組合拱圈，如圖2 所示，鋼混界面采用剪力連接件連接，結構基礎一般采用擴大基礎或樁基礎，主體結構上覆結構性回填料，形成土體-混凝土-波紋鋼板組合承載體系。

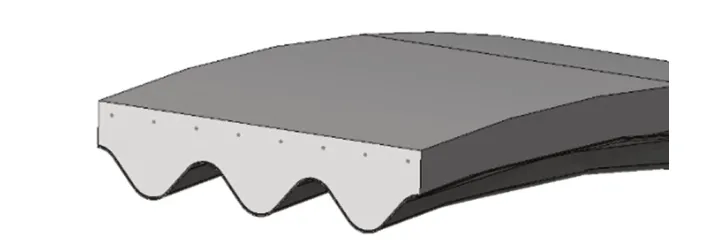
圖2 典型覆土波紋鋼板混凝土組合拱橋截面形式示意圖

由于該類橋型是一種新的結構形式，相關研究主要對波紋鋼板混凝土組合構件的軸壓性能、抗彎承載能力[2，3]以及界面剪切滑移性能[4]進行了試驗研究。驗證了該組合構件的可行性，但是在整體結構的設計和計算方法層面研究極少。

本文以覆土波紋鋼板混凝土組合拱橋為研究對象，探討既有計算理論和模型應用于該結構的可行性，并通過3D 及2D 有限元模型考察了不同混凝土覆層厚度及填高工況下結構整體剛度和變形特性，最后通過CANDE 軟件對內蒙古自治區省道203 線阿爾山-烏蘭浩特公路某覆土波紋鋼板-混凝土組合橋進行建模計算分析。

2 計算模型探討

既有結構形式中，埋置式排水管道、公路隧道、混凝土涵洞同覆土波紋鋼板橋涵結構形式類似，既有結構計算模型和設計方法對覆土波紋鋼板橋涵結構具有一定的借鑒意義。通過分析幾種相關結構的計算模型和設計方法，探討其適用于該新橋型的可行性。

2.1 相關結構計算方法

《給水排水工程管道結構設計規范》（GB 50332-2002）[5]中將埋置管道劃分為柔性管道和剛性管道兩大類，并在設計中區分對待，對于圓形管道結構，規范中引入管道結構同管周土體剛度比值αs作為劃分圓形管道剛柔類別的標準。αs計算方法見式（1）。

式中，Ep為管材的彈性模量，MPa；Ed為管側土的變形綜合模量，MPa；t為圓管的管壁厚度，mm；r0為圓管結構的計算半徑，mm。規范將αs<1的圓形管道歸入柔性管道范疇，將αs≥1的圓形管道、矩形管道及拱形管道歸入剛性管道范疇。對于柔性管道，需充分考慮土體-結構相互作用效應，規范中所用變形計算公式依然沿用Spangler[6]所提的經驗公式；對于剛性管道可忽略管體結構的變形影響，采用簡單的荷載結構模型進行計算。值得注意的是，規范中明確提出對于凈寬度大于3m的矩形或拱形結構，需采用管道-地基共同作用模型進行靜力計算。

《公路隧道設計規范》（JTG D70-2004）[7]中規定，公路隧道的襯砌設計應采用荷載結構模型進行計算。《公路涵洞設計細則》（JTGT D65-04-2007）[8]中同樣引入公式（1）所提的剛度相對系數，并認為大部分圓管涵為剛性管，可采用荷載結構模型計算結構內力響應。對于圓形混凝土埋置管涵，CHBDC[9]和AASHTO[10]規范中均采用Heger壓力分布模型（圖3）進行設計計算。

圖3 圓形混凝土管結構Heger壓力分布模型示意圖

對于覆土波紋鋼板橋涵結構，已有研究大多集中于加拿大和北歐，早期計算模型為相對簡單的環壓理論模型，AISI、ASTM、AASHTO 等規范中大都以環壓理論作為基礎，AASHTO 規范[10]后續引入相關研究成果，對環壓理論在大跨度結構等特殊工況中的應用做了改善。20世紀70年代Duncan提出的SCI法[11]成為被廣泛認可的覆土柔性橋涵計算方法，基于該理論的衍生方法，較為常用的主要有CHBDC方法[9]和Pettersson-Sundquist方法[12]。CHBDC方法和Pettersson-Sundquist方法中在計算結構的正截面彎矩時，均引入剛度對比系數Nf對不同線型、不同跨度、不同截面形式的結構進行區分計算。剛度對比系數Nf計算見式（2）。

式中，Es為土體剪切模量，MPa；Dh為結構跨度，mm；E 為主體結構材料彈性模量，MPa；I 為主體結構單位長度正截面慣性矩，mm4/mm。

總結以上類似結構的設計計算模型可知，模型主要分為兩大類，一類為考慮土體-結構相互作用的整體模型，模型中考慮土體-結構的相互影響，能夠相對較準確的反應結構內力分布情況，一般適用于柔性結構或跨度較大的剛性結構。另一類模型為荷載-結構模型，該模型將覆土、車輛等各種作用以等效荷載的形式加載在主體結構上，模型大多用于小跨度剛性結構的設計計算，且多數情況下將導致過于保守的設計結果。對于覆土波紋鋼板混凝土組合拱橋，考慮土體-結構相互作用的整體模型是可行的，但既有的基于有限元分析的衍生方法是否需要改進有待研究，同時簡單易行的荷載-結構模型是否可行也有待分析。

2.2 有限元模型

規范[10]中提出可采用專用有限元程序SPIDA 進行混凝土管涵的土體-結構相互作用分析及設計，并提出可采用專用有限元程序CANDE 進行柔性覆土金屬管涵的結構計算和設計。各種大型通用有限元軟件，如ABAQUS、ANSYS 等，均可用于該類結構的建模分析和計算。

采用有限單元法進行覆土管涵、覆土拱橋分析的相關研究數量較多，該類模型的普遍特點是將原位土體、回填土體和主體結構一并體現在模型中，并通過適當的接觸關系模擬土體-結構的相互作用，從而得到相對準確的結構內力分布。

有限元計算平臺可選項較多，需根據具體問題具體分析，選擇合適的數值模型、合適的計算軟件進行計算。

3 新結構特性有限元分析

作為一種新型結構，對覆土波紋鋼板混凝土組合拱橋依照整體剛度和變形特性進行定性分類，有助于更好的選擇合適的設計計算方法。通過相對剛度系數法對該結構的整體剛度做區分，并輔以2D、3D 有限元模型線性屈曲分析，通過對線性屈曲模態的區別，進一步印證結構的整體類型劃分。

3.1 相對剛度系數計算

以本項目依托工程備選方案為例，如圖7方案A所示，擬建覆土鋼混組合橋跨度為13m，矢高為5.89m，周邊回填料變形綜合模量取20MPa，用公式（1）進行計算。組合截面采用等效后的截面厚度和彈性模量計算。等效計算公式見式（3）。

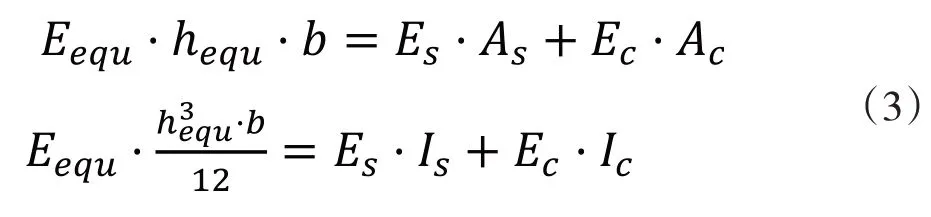
式中，Eequ為等效截面彈性模量，MPa；hequ為等效截面厚度，mm；b 為計算寬度，mm，可取為單位寬度；Es為波紋鋼板的彈性模量，MPa；Ec為混凝土材料彈性模量，MPa；As為單位寬度波紋鋼板正截面面積，mm2/mm；Ac為單位寬度混凝土覆層正截面面積，mm2/mm，其中處于波紋鋼板波谷內的混凝土可作為剪力連接件組成部分，不計入正截面剛度計算；Is為單位寬度波紋鋼板抗彎慣性矩，mm4/mm；Ic為單位寬度混凝土抗彎慣性矩，mm4/mm。參考規范[6]計算結果及結構剛度&柔度判別見表1。

經計算可知，當混凝土覆層厚度增大時，主體結構剛度逐漸增大，因此結構同周圍土體的相對剛度系數也逐漸增大，從100mm 覆層的0.07 增長至900mm 覆層的6.73，參照規范[5]規定，當混凝土覆層厚度為300mm及以下時，結構為柔性結構，需考慮土體-結構的相互作用；當混凝土覆層厚度為500mm及以上時，結構為剛性結構，可采用荷載-結構模型進行計算和設計。

3.2 3D模型屈曲模態分析

結構的屈曲模態能夠在一定程度上反映結構的剛度特性，通過精細3D 模型的線性屈曲有限元分析，考察結構的剛度特性，并同上節的結構剛度和柔性劃分對比驗證。

該有限元模型僅以主體拱圈為研究對象，不考慮土體作用，波紋鋼板及混凝土的材料特性見表2，采用綁定連接將鋼混結構連接成為一個整體，線性屈曲單位荷載為拱圈上表面的環壓均布荷載。此處同樣考慮多種不同混凝土覆層厚度的計算結果，覆層厚度分別取100mm、300mm、500mm、700mm、900mm，并取線性屈曲的第一階屈曲模態進行對比，各個模型計算結果如圖4所示。

圖4 不同混凝土覆層厚度模型一階屈曲模態計算結果

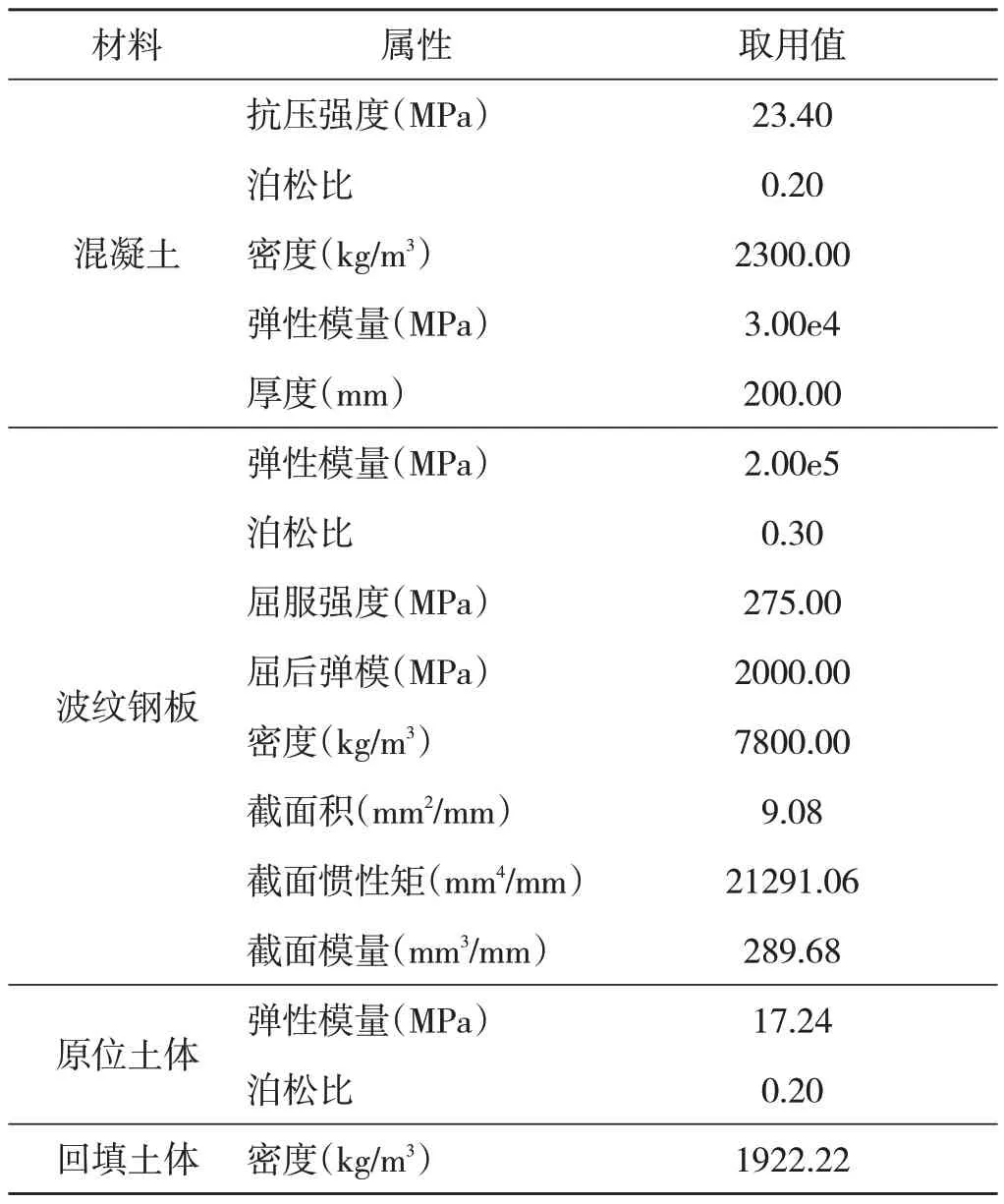
表2 材料特性參數取值

從主體結構拱圈的計算結果可知，當混凝土覆層厚度為500mm 及以下時，結構的一階屈曲模態為整體屈曲模態，表征此時結構整體剛度相對較小；當混凝土覆層厚度為700mm 及以上時，結構一階屈曲模態為局部屈曲，表征此時結構的整體剛度相對較大。該計算結果印證了上節計算結果，其中，500mm覆層的結構同100mm 覆層結構的變形特性類似，而上節計算結果表明，500mm覆層結構應歸化為剛性結構，當混凝土覆層處于500mm 左右時，相對剛度系數接近劃分閾值1，此時結構處于剛性結構、柔性結構的過渡區域，難以嚴格定性，但從結構設計和計算角度看，應趨于保守的將結構歸化為柔性結構。

3.3 2D模型屈曲模態分析

通過結構線性屈曲模態分析結構整體剛度和變形特性，同時考慮上覆土層厚度對結構的影響。為避免計算量過大，采用2D土體-結構相互作用模型，土體采用線彈性模型，并采用平面四邊形單元模擬，彈性模量為20MPa，泊松比為0.2，拱橋兩側分別取2.5 倍跨徑土體寬度[13]；主體結構混凝土及波紋鋼板材料參數同上節，并分別采用梁單元模擬，混凝土覆層同波紋鋼板之間采用connector 單元模擬，混凝土覆層同土體之間采用綁定連接。線性屈曲單位荷載取用土體頂面均布壓力。當覆土厚度為3m時，不同混凝土覆層厚度模型一階屈曲模態如圖5所示。

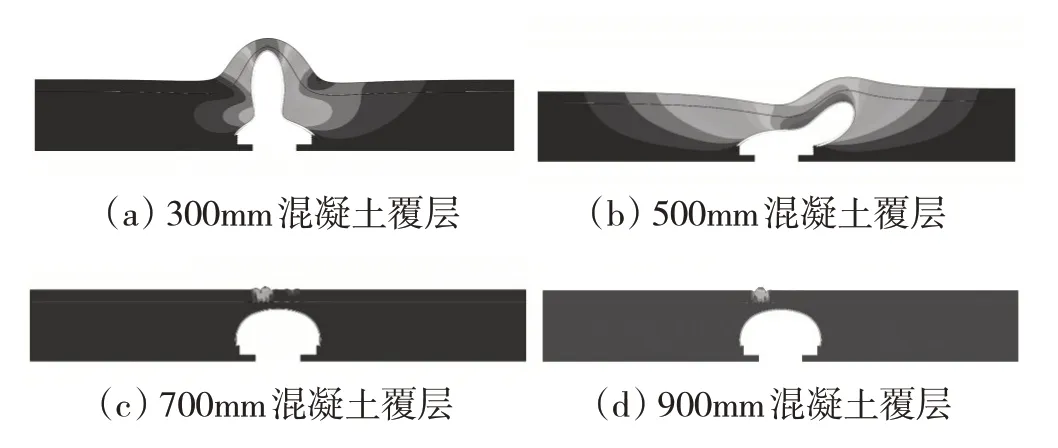
圖5 3m覆土厚度模型一階屈曲模態示意圖

結果表明，當混凝土覆層厚度為500mm及以下時，覆土鋼混組合結構一階屈曲模態為主體結構及土體整體失穩；當混凝土覆層厚度為700mm及以上時，屈曲模態為土體表層局部位置的失穩。該模型不能捕捉到組合結構局部失穩的模態，但是總體結果同上節相吻合，即對于該固定線型和跨度的覆土鋼混組合拱橋，混凝土覆層厚度超過一定限值時，結構整體剛度相應增大，致使整體屈曲模態剛度超限，不再成為可以控制失穩的模態。

當覆土厚度為50m 時，不同混凝土覆層厚度模型一階屈曲模態如圖6所示。

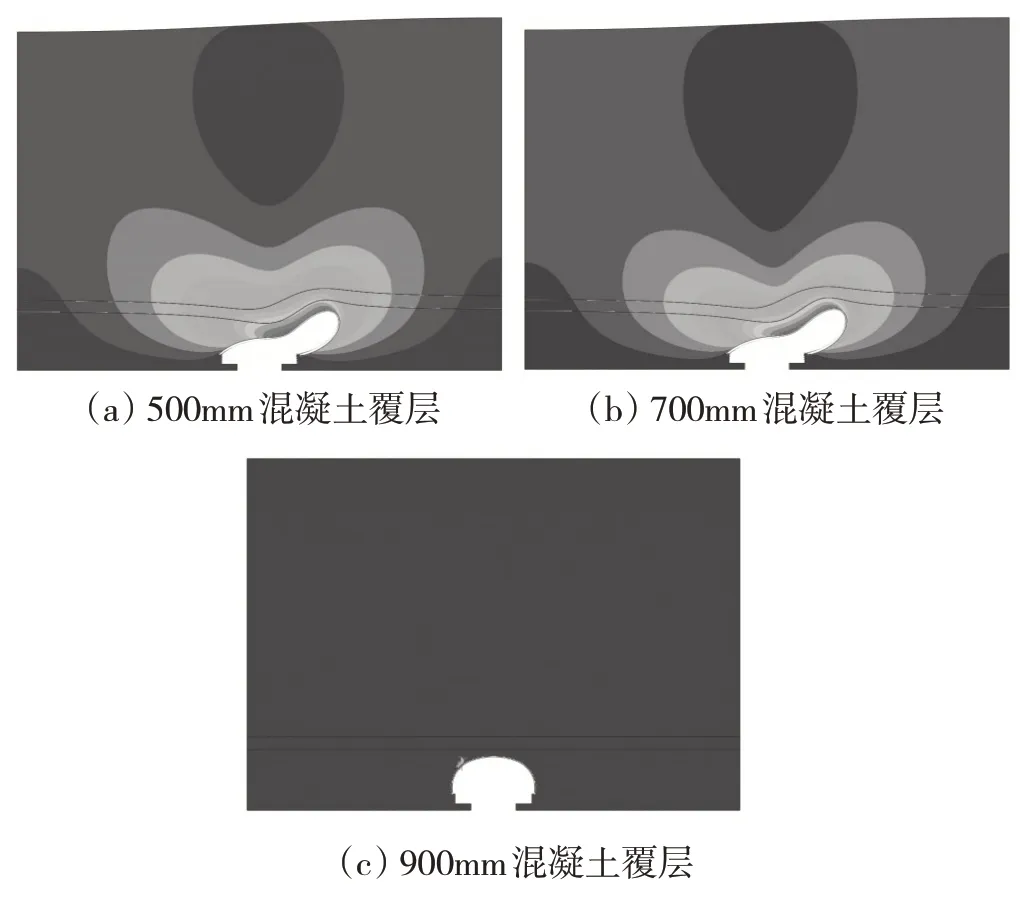
圖6 50m覆土厚度模型一階屈曲模態示意圖

結果表明，對于50m 覆土工況，覆土鋼混組合結構一階屈曲模態從整體失穩轉變為土體局部失穩的轉變點有所變化，對于700mm混凝土覆層的結構，當上覆土層為3m 時，主體結構相對剛度較大，基礎失穩模態為土體局部失穩，但隨著覆土厚度變為50m，主體結構相對剛度顯著下降，因此，一階失穩模態變為主體結構的整體失穩。計算結果表明，當主體結構-周邊土體相對剛度發生變化時，結構的整體變形特性將會在某個工況點發生質的變化。

以上有限元計算結果表明，通過相對剛度系數對結構進行剛性&柔性劃分是有意義的，當結構屬于柔性結構時，在結構設計和計算中必須考慮土體-結構的相互作用；當結構屬于剛性結構時，可適當放寬模型要求，但對于處于過渡區域的工況，應保守的采用土體-結構相互作用模型進行設計和計算。

4 設計案例

選用專業有限元分析軟件CANDE 進行依托工程的建模分析。CANDE軟件為一款面向覆土橋涵和地下結構的專用軟件。其模型可考慮土體非線性、結構材料非線性，以及土體-結構相互作用，同時采用分施工階段建模分析，能夠得到相對準確的結構響應。

4.1 工程概況

擬在內蒙古自治區省道203 線阿爾山至烏蘭浩特公路修建鋼混組合波紋鋼板拱形小橋。在里程K104+044位置擬建跨徑13m拱橋，該里程位置原設計橋梁最低樁頂標高為686.70m，設計高程為697.61m，填挖高度為10.91m。經過初步查閱資料及計算，擬在如圖7所示兩種方案中選擇最優方案。

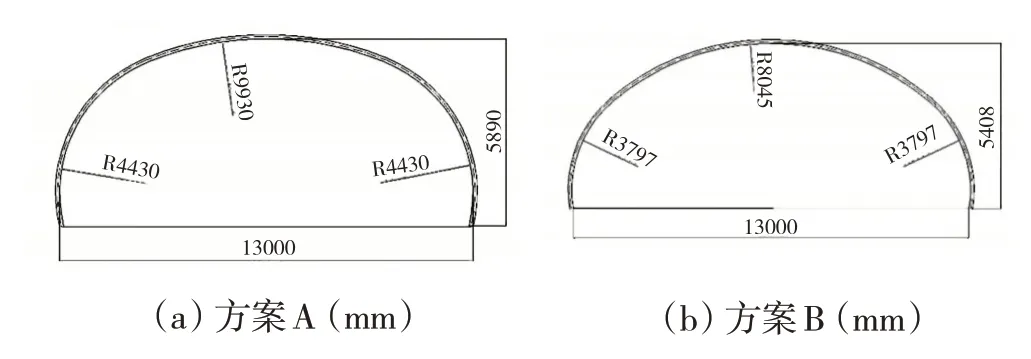
圖7 某覆土波紋鋼板-混凝土組合橋線型初選方案

4.2 有限元模型

模型中主體結構拱線采用兩種不同線型進行對比分析，覆土厚度為3.1m。橋梁擬采用波紋鋼板-混凝土組合結構，其中混凝土采用C35 混凝土，根據規范[14]規定，混凝土抗壓強度為23.4MPa，混凝土覆層200mm，靠外側設置直徑24mm、間距150mm單層鋼筋，鋼筋材料采用HRB335鋼筋。波紋鋼板采用380mm×140mm×7mm波形，Q345 鋼材，根據規范[15]規定，鋼板屈曲強度采用275MPa。原位土體采用線彈性本構，回填料采用Duncan/Selig本構模型。所有材料的物理特性參數及幾何參數見表2，鋼板及混凝土的本構關系曲線如圖8所示。

CANDE 模型采用平面單元模擬土體，梁單元模擬拱圈結構，模型底部邊界固結，側邊界允許豎向滑移。模型中考慮的作用主要為土體和結構自重，另在施工完成后考慮規范[16]中的車輛荷載作用。

土體與結構之間采用允許滑移的連接單元模擬，混凝土覆層與波紋鋼板之間采用普通的連接單元連接，鉸接（pinned link）單元僅約束被連接結點的平動自由度，剛接（rigid link）單元則約束被連接結點的所有自由度，兩種連接單元能夠表征組合結構實際情況的上下限，因此，分別用兩種連接單元進行計算，最終結果作為包絡曲線進行分析。模型如圖9所示。

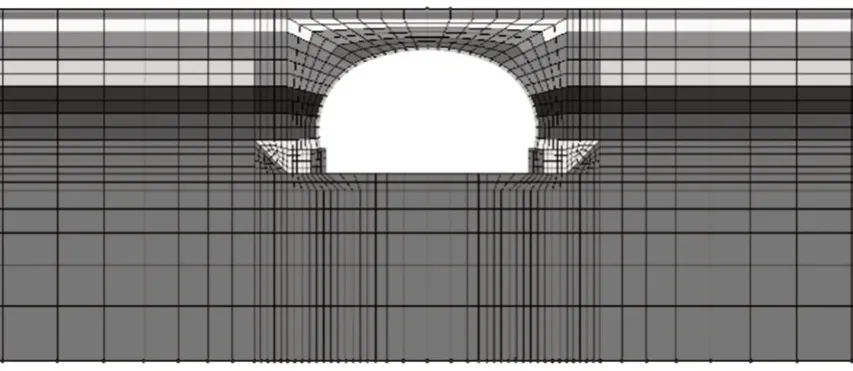
圖9 CANDE模型示意圖

4.3 結果分析

計算表明，兩種不同連接單元的模型計算結果相差不大，如圖10所示，A-fix代表方案A線型+剛性連接單元，A-pin代表方案A線型+鉸接單元，B-fix代表方案B 線型+剛性連接單元，B-pin 代表方案B 線型+鉸接單元。方案A 拱頂下撓140.8mm，基座沉降72.9mm，拱線豎向相對變形為67.9mm；方案B 拱頂下撓153.8mm，基座沉降80.4mm，豎向相對變形為73.4mm。從變形角度考慮，方案A占優勢。

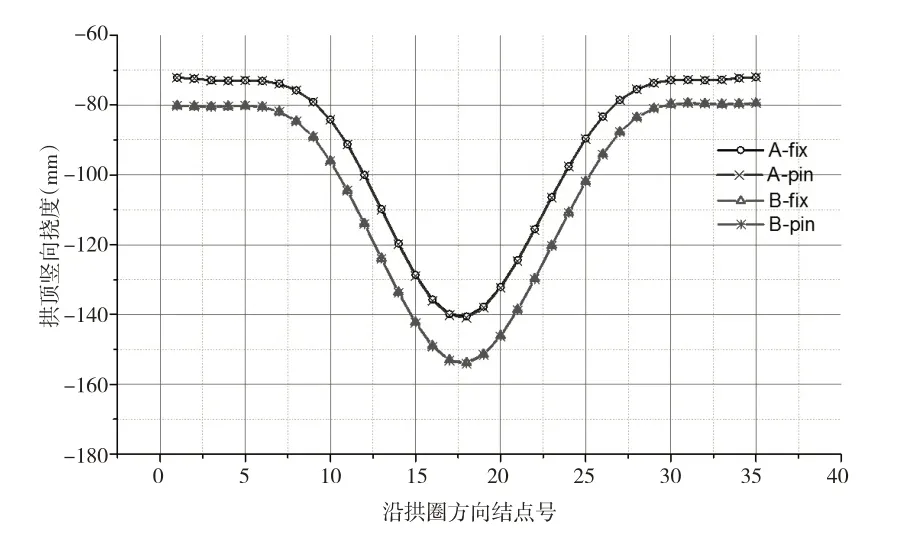
圖10 豎向撓度對比

三個關鍵位置的應力信息如圖11 所示，在拱頂至拱肩位置，兩種方案的應力分布相差不大，但是在拱肩至拱腰區間內，方案A 的應力均小于方案B 的應力分布，該應力分布情況反映出方案A拱線線型對應的內力（軸力、彎矩）分布相對更合理。因此，從應力分布情況考慮，方案A占優勢。

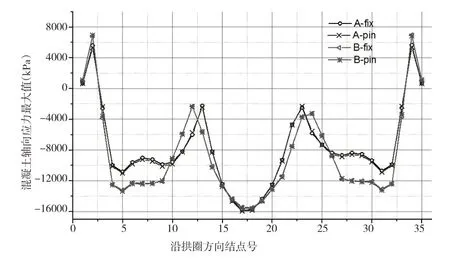
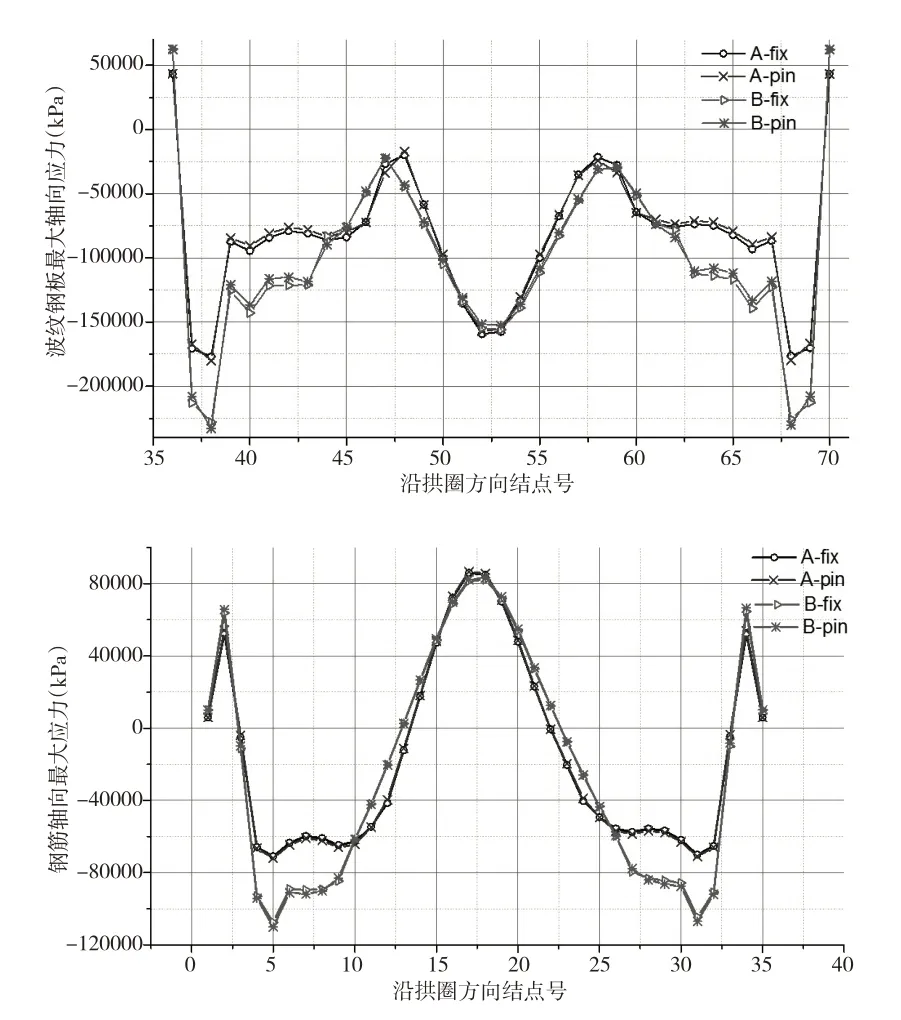
圖11 混凝土、波紋鋼板及鋼筋最大應力分布

拱腳推力見表3，相對小的拱腳推力對后續基礎設計有利，從拱腳推力角度考慮，方案A占優勢。

表3 四個模型的拱腳推力對比

從上述對比分析可知，CANDE 軟件中采用兩套梁單元+不同連接單元模擬組合結構是可行的，計算結果表明線型方案A力學行為相對更優，建議后續設計基于該方案開展工作。

5 結語

①對于覆土波紋鋼板混凝土組合拱橋而言，考慮土體-結構相互作用的整體模型是可行的，但既有的基于有限元分析的衍生方法是否需要改進有待研究，同時簡單易行的荷載-結構模型是否可行也有待分析。

②考慮土體-結構相互作用的有限元模型，用于覆土波紋鋼板混凝土組合結構的計算分析是可行的，有限元計算平臺可選項較多，需根據具體問題具體分析，選擇合適的數值模型、合適的計算軟件進行計算，模型的準確性需通過試驗和監測數據加以驗證。

③通過相對剛度系數對結構進行剛性、柔性劃分是有意義的，當結構屬于柔性結構時，在結構設計和計算中必須考慮土體-結構的相互作用；當結構屬于剛性結構時，可適當放寬模型要求，但對于處于過渡區域的工況，應保守的采用土體-結構相互作用模型進行設計和計算。

④設計案例表明，專用程序CANDE 可用于覆土波紋鋼板混凝土組合拱橋的設計和分析。