基于回波預處理和相參積累的C&I干擾抑制算法

張 亮, 王國宏, 孫殿星, 于亦文, 張翔宇

(1. 海軍航空大學信息融合研究所, 山東 煙臺 264001;2. 中國人民解放軍94326部隊, 山東 濟南 250000;3. 中國電子科技集團儀器儀表有限公司, 山東 青島 266555)

0 引 言

雷達電子對抗是信息化戰爭的重要組成部分,強干擾背景下為有效發揮雷達效能,針對特定干擾樣式研究相應對抗方法尤為重要[1]。C&I(chopping and interleaving)干擾和頻譜彌散(smeared spectrum, SMSP)干擾是Sparrow等人發明的兩種針對線性調頻(linear frequency modulation, LFM)脈沖壓縮雷達的典型干擾樣式[2]。區別于全脈沖復制轉發密集假目標干擾[3],C&I干擾和SMSP干擾由雷達信號脈內調制生成,單個干擾信號經雷達匹配濾波器即可輸出高密度虛假目標群,欺騙兼壓制雷達系統。不同于SMSP干擾,C&I干擾子信號調頻斜率與雷達發射信號調頻斜率相同,SMSP干擾抑制算法[4-9]對C&I干擾難以有效適用[10-12]。為對抗C&I干擾,文獻[13-14]提取回波特征參數,利用分類器識別回波類型,由于缺乏必要抑制環節,算法不適用于自衛式干擾。為提高算法適用范圍,文獻[15]從C&I干擾假目標生成機理出發,設計了一種多普勒稀疏敏感波形,用于抑制干擾在多普勒上的連續輸出,但波形設計會增加發射機復雜度,且所設計波形多普勒容許度較低。文獻[16]以LFM雷達中一個相干處理間隔(coherent process interval, CPI)回波為處理對象,通過快慢時間域聯合處理，估計干擾位置、幅度等參數重構干擾信號,通過對消實現干擾抑制,但全參數估計較為復雜,累積誤差對干擾對消效果影響較大。考慮到C&I干擾波形與間歇采樣轉發干擾相似[17],頻譜由雷達信號頻譜疊加而成,干擾信號等同于多分量移頻干擾。對于單分量移頻干擾,其匹配輸出峰值位置取決于發射信號調頻斜率和移頻量[18-19],當發射信號脈間調頻斜率捷變[20-21],由于不同重復周期內假目標快時間位置不同,經相參積累可達成干擾抑制目的,理論上該方法同樣可抑制C&I干擾,但脈間調頻斜率捷變同樣會增加發射機復雜度。

針對上述問題,以不具備調頻斜率捷變常規LFM雷達抗自衛式C&I干擾為背景,提出基于回波預處理和相參積累的干擾抑制算法。首先,對回波慢時間做快速傅里葉變換(fast Fourier transform, FFT)估計回波時延(快時間不做處理);其次,根據回波時延設置距離窗截取受干擾回波段;再次,設計M種不同調頻斜率LFM參考信號(M為相參積累個數),分別對雷達發射信號和各重復周期回波進行乘積調制;然后,以調制后的發射信號為匹配信號,依次對調制后各重復周期回波進行脈沖壓縮,改變不同重復周期假目標快時間位置分布;最后,對預處理回波慢時間相參積累,實現干擾抑制。

1 干擾特性分析

雷達發射LFM脈沖信號,零中頻復數形式為

s(t)=rect(t/Tp)eiπkt2

(1)

式中:Tp為脈寬,k=B/Tp為調頻斜率,B為帶寬。根據相位駐留原理,當TpB1時,s(t)頻譜可近似表示為

(2)

設采樣脈沖串p(t)脈寬為τ、采樣周期為Ts,利用p(t)采樣雷達信號,復制次N-1次,拼接得到C&I干擾為

(3)

JCI(f)=[sin(πNτf)/sin(πτf)]·

(4)

式中:fs=1/Ts為間歇采樣頻率;sin(πfNτ)/sin(πfτ)為頻域采樣函數。式(4)可簡化為

JCI(f)=[sin(πNτf)/sin(πτf)]·

(5)

式中:an=sinc(πτnfs)τ/Ts。可以看出,C&I干擾頻譜為雷達發射信號頻譜周期延拓、幅度加權、線性疊加和頻域采樣,干擾信號時域可理解為多分量移頻干擾(移頻量為nfs),由于LFM固有距離-多普勒的耦合特點,自衛式干擾下干擾信號經雷達匹配濾波器生成虛假目標群,且部分假目標導前真實目標。設自衛式干擾機為點目標,徑向速度為vt,初始距離為Rt,速度矢量與雷達夾角為0°,目標雷達散射截面(radar cross section, RCS)不起伏,雷達在干擾機方位接收真實回波基帶信號為

(6)

(7)

式中:Aj為干擾幅度;fd(tm)為干擾多普勒頻率函數。設fd(tm)=0,不考慮慢時間對回波時延影響,雷達接收受干擾回波可簡化為

(8)

(9)

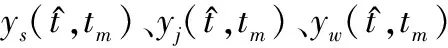
(10)

2 干擾抑制原理

2.1 回波預處理

由第1節分析可知,C&I干擾可理解為移頻量為nfs的多分量移頻干擾。為方便分析,假設C&I干擾包含1個移頻分量,即

jCI(t)=s(t)ei2πfst

(11)

令j(t)=jCI(t),根據傅里葉變換頻移性質,得到j(t)頻譜為

(12)

忽略常復數項e-i4πRt/λ,由式(8)可知,第1個脈沖重復周期雷達接收回波信號為

xr(t)=σs(t-t0)+Ajj(t-t0)+w(t)

(13)

yr(t)=ys(t)+yj(t)+yw(t)=σTp·
sinc[πB(t-t0)]+yw(t)+Aj(Tp-|fs|/k)·
sinc[π(B-|fs|)(t-t0+fs/k)]eiπfs(t-t0)

(14)

式中:ys(t),yj(t),yw(t)分別為第一個重復周期真實回波、干擾分量和噪聲脈壓結果,真實回波、干擾分量脈壓后均為sinc函數,峰值位置分別為t0和t0-fs/k。設距離窗覆蓋真實回波與干擾信號[22-23],距離范圍為R1～R2,則距離窗可表示為

win(t)=rect[(t-t1)/Tw]

(15)

式中:Tw=2(R2-R1)/c為窗寬度;t1=(R1+R2)/c為窗中心。根據距離窗設計參考信號

ref1(t)=win(t)eiπk1(t-t1)2

(16)

式中:k1為參考信號調頻斜率,且k1>-k。利用參考信號對第1個重復周期回波進行乘積調制,得到

(17)

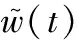
(18)

(19)

(20)

(21)

(22)

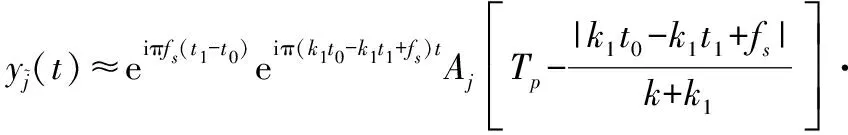
(23)

(24)

(25)

當t1=t0時,調制后的真實回波脈壓峰值位置為0,與參考信號調頻斜率k1無關,而干擾分量峰值位置為-fs/(k+k1),與k1有關。如果對M個重復周期回波使用M種不同調頻斜率參考信號調制,真實回波脈壓峰值位置恒等于0,而干擾峰值位置均不相同,對預處理回波慢時間相參積累可實現干擾抑制。

2.2 回波時延估計

回波預處理要求距離窗中心t1=t0,為估計回波時延,忽略常復數項e-i4πRt/λ,重寫式(8)為

(26)

(27)

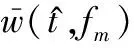
(28)

對式(28)進行一階差分即可估計回波時延。綜上所述,圖1給出了干擾抑制流程。圖1中設計參考信號,調頻斜率的選取應確保參考信號及調制后回波、雷達信號滿足采樣定理[24-25]。

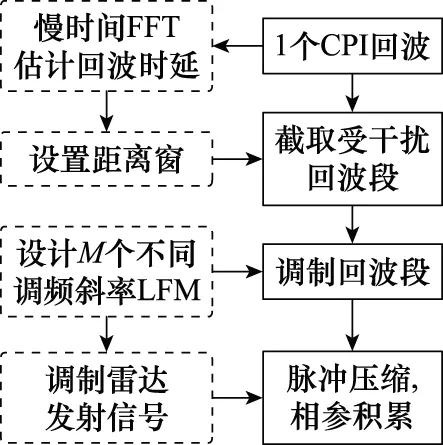
圖1 干擾抑制流程Fig.1 Jamming suppression process

3 仿真結果與分析

3.1 參數設置

設雷達載頻為0.4 GHz,重頻為2 KHz,發射信號為LFM脈沖信號,脈沖寬度為0.1 ms,帶寬為4 MHz,采樣頻率為帶寬的4倍,相參積累個數設置為128;干擾機(真實目標)多普勒頻率為250 Hz,徑向距離為30 km,回波幅度為1 V,根據回波幅度確定信噪比(signal to noise ratio, SNR)和干信比(jamming to signal ratio, JSR);C&I干擾利用脈沖串(采樣周期為20 μs,采樣脈寬為5 μs)采樣雷達信號復制3次生成。

3.2 算法流程仿真分析

設SNR為-10 dB、JSR為20 dB,圖2為1個CPI受干擾回波。對回波快時間脈沖壓縮、慢時間相參積累,結果如圖3所示。C&I干擾經相參積累生成分布真實目標前后相干假目標串,假目標寬度約20 km。

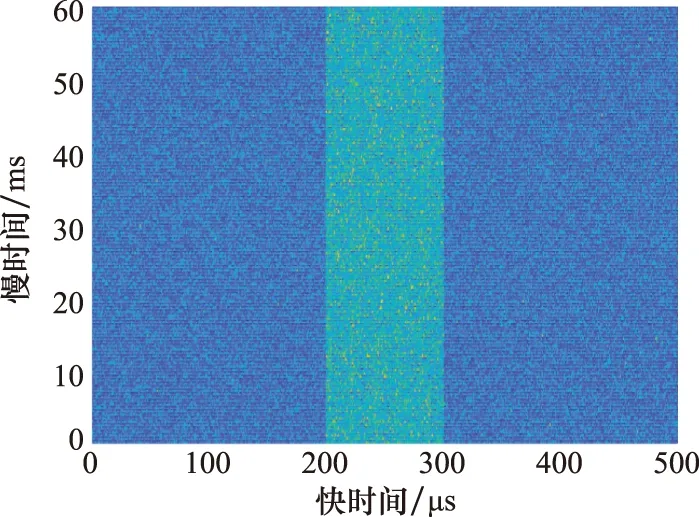
圖2 1個CPI回波Fig.2 Echo signal within a CPI

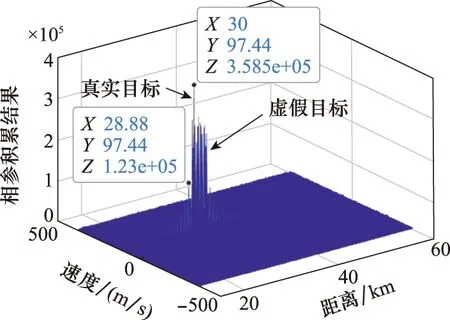
圖3 受干擾回波相參積累結果Fig.3 Result of jammed echo coherent integration

根據圖1干擾抑制流程,對原始回波慢時間作FFT,結果如圖4所示。可以看出,即使不對回波進行快時間脈沖壓縮,真實回波和干擾信號同樣能夠獲得相參處理處理增益,與理論分析一致。對慢時間FFT結果取包絡,沿快時間求和,結果如圖5所示,真實目標徑向速度為97.44 m/s。取對應快時間信號,一階差分結果如圖6所示,估計得到真實目標徑向距離為30 km,與仿真參數一致。根據虛假目標分布范圍,設置寬度45 km距離窗(中心位置為37.5 km),截取受干擾回波段。設計128個不同調頻斜率LFM參考信號(參考信號調頻斜率在-20～60 GHz/s范圍內隨機選取),以調制后的發射信號為匹配信號,對調制后的各脈沖重復周期回波進行脈沖壓縮,預處理結果如圖7所示。可以看出,不同重復周期真實目標脈壓峰值快時間位置不變,假目標位置均發生變化。對回波預處理結果慢時間相參積累結果如圖8所示,虛假目標得到有效抑制。

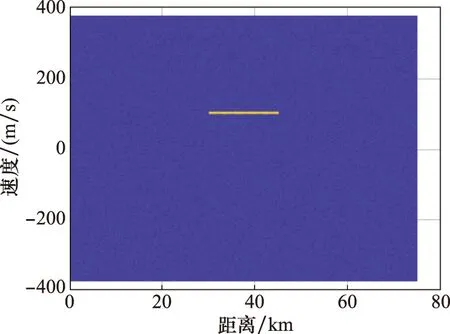
圖4 回波慢時間FFT結果Fig.4 Slow-time FFT result of echo

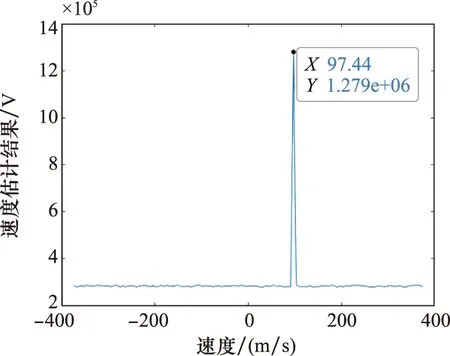
圖5 真實目標徑向速度估計結果Fig.5 Radial velocity estimation result of real target

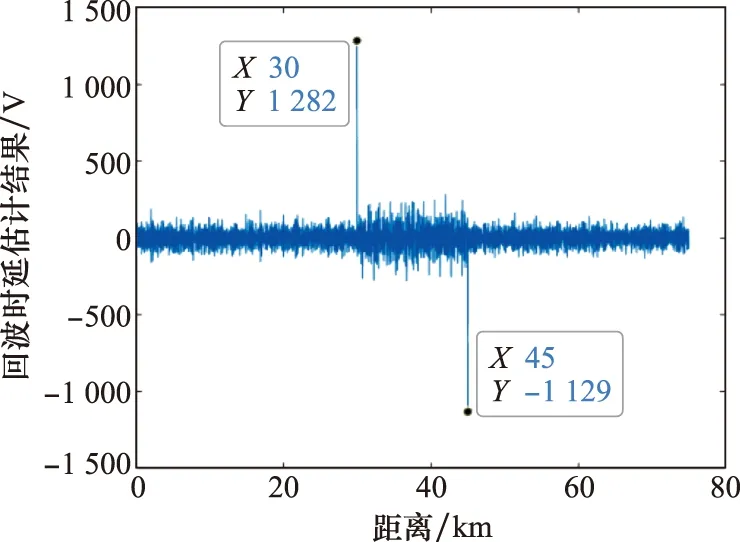
圖6 回波時延估計結果Fig.6 Echo delay estimation result

圖7 回波預處理結果Fig.7 Echo preprocessing result

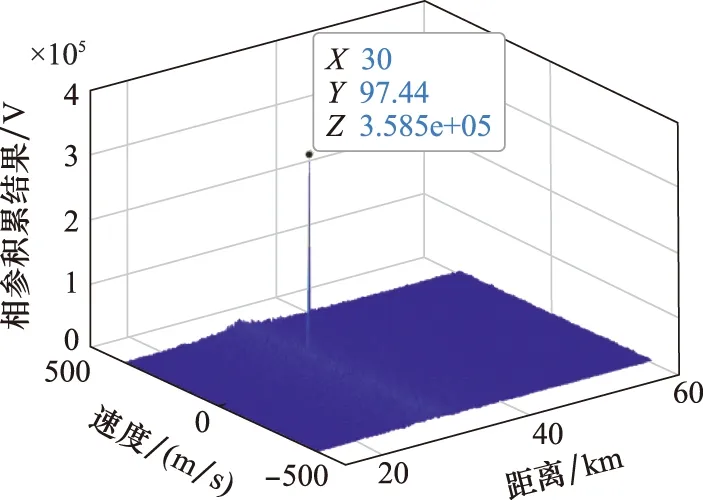
圖8 干擾抑制效果Fig.8 Jamming suppression effect

3.3 算法效能仿真分析

首先,以平均絕對誤差(mean absolute error, MAE)為指標,分析所提慢時間FFT方法回波時延估計精度。為保證通用性,SNR分別取-10 dB、-5 dB和0 dB,JSR取0 dB至50 dB,間隔5 dB,蒙特卡羅500次,回波前沿估計MAE隨JSR變化曲線如圖9所示。當JSR大于等于15 dB時,不同SNR條件下慢時間方差法[16]和所提方法均能準確估計回波前沿,當JSR小于15 dB時,所提方法估計精度優于慢時間方差法。其次,評估算法虛假目標抑制效能,定義虛假目標抑制率(false target suppression ratio, FTSR)為

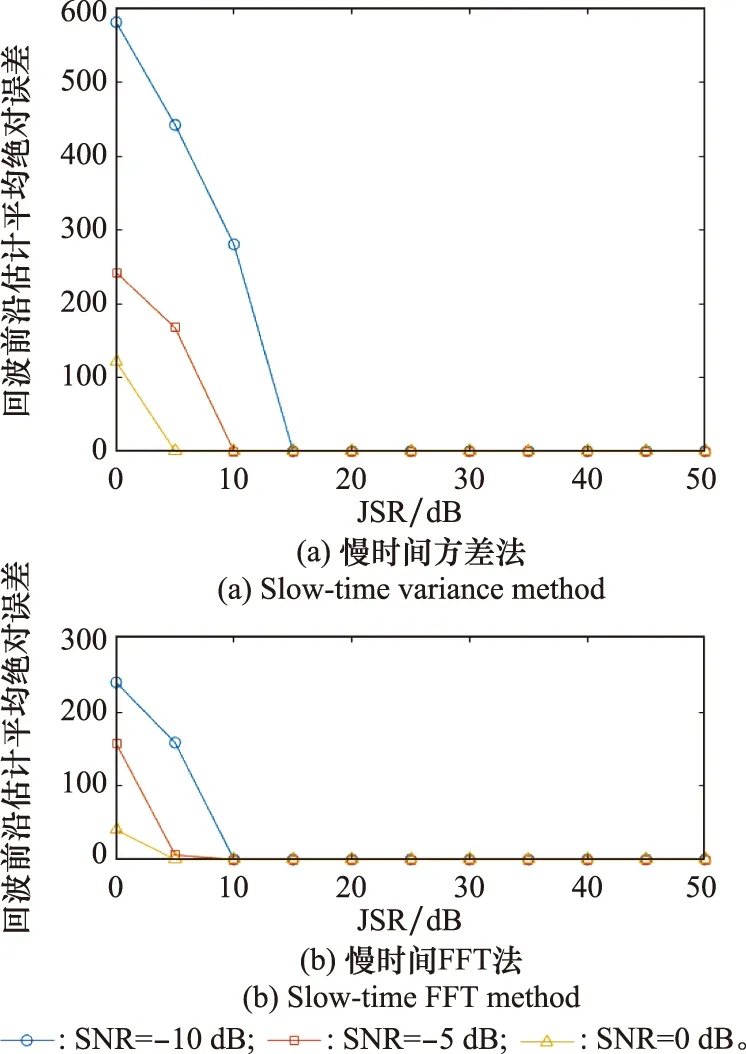
圖9 回波前沿估計MAE隨JSR變化曲線Fig.9 Curves of echo frontier estimation MAE with JSR

(29)

式中:FTSR單位為百分比;num1i為第i次蒙特卡羅抑制前虛假目標數量;num2i為抑制后虛假目標數量。SNR取值同上,JSR取15 dB至50 dB,間隔5 dB,利用二維單元平均恒虛警檢測器對抑制前后處理結果進行檢測,圖10給出了FTSR隨JSR變化曲線。兩種算法對虛假目標均能達成一定抑制效能,干擾抑制后假目標數量明顯減少,FTSR均大于40%。

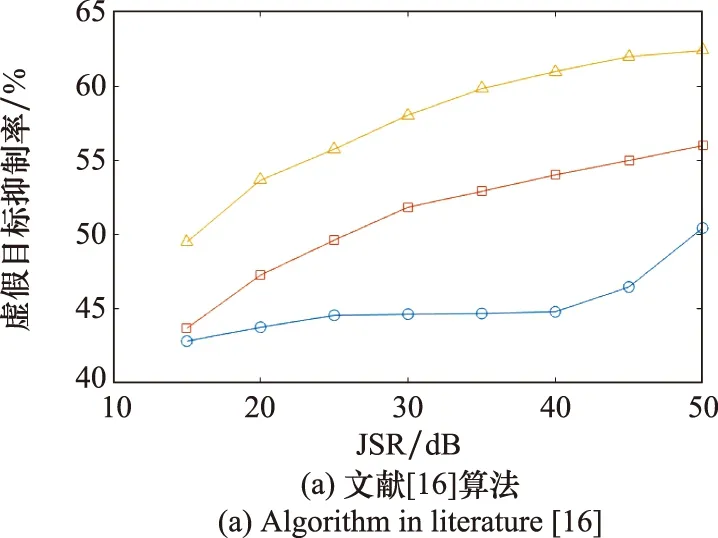
圖10 FTSR隨JSR變化曲線Fig.10 Changing curves of FTSR with JSR

最后,以真實目標檢測率[6](real target detected ratio, RTDR)為指標,評估算法對真實目標檢測改善程度。SNR、JSR、蒙特卡羅次數同上,RTDR隨JSR變化曲線如圖11所示。可以看出,干擾抑制前當JSR大于20 dB時,不同SNR條件下RTDR均為0,雷達檢測不到真實目標,文獻[16]干擾抑制后,真實目標檢測率明顯提高,但隨JSR的增大RTDR呈一定下降趨勢,當JSR增大至45 dB,不同SNR條件下RTDR接近于0,而本文算法不同SNR、JSR條件下RTDR均接近100%,真實目標檢測效能優于對比算法。

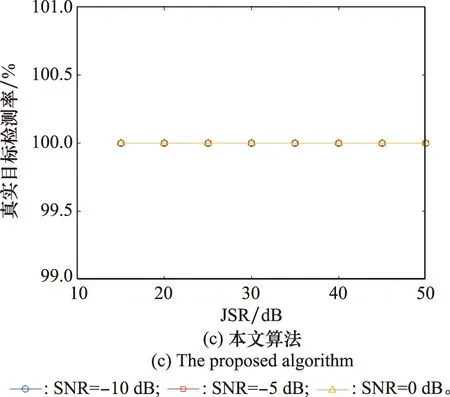
圖11 RTDR隨JSR變化曲線Fig.11 Changing curves of RTDR with JSR

4 結 論

自衛式干擾下C&I干擾信號之所以能夠獲得相參處理增益是因為干擾快時間匹配輸出與慢時間無關,對回波進行預處理,使干擾快時間匹配輸出與慢時間耦合,慢時間相參積累可實現干擾抑制。基于該思路,提出基于回波預處理和相參積累的C&I干擾抑制算法,算法無需改變雷達發射波形,僅涉及信號層處理,適用常規LFM雷達。仿真結果表明,當SNR大于-10 dB、JSR小于50 dB,所提算法能夠有效抑制C&I干擾,干擾抑制后真實目標檢測率接近100%,虛假目標抑制率大于45%。