基于多尺度網格細胞的路徑整合模型
趙辰豪, 吳德偉, 韓 昆, 朱浩男, 代傳金
(空軍工程大學信息與導航學院, 陜西 西安 710077)
0 引 言
近年來,智能導航技術成為導航技術發展的主流趨勢。隨著網格細胞[1]、位置細胞[2],頭朝向細胞[3]、速度細胞[4]、邊界細胞[5]等大腦內導航細胞的發現,產生了一種新的智能導航技術——類腦導航[6]。類腦導航作為新興的智能導航技術,主要通過模擬大腦的空間表征機制[7],導航信息處理機制與記憶機制[8],實現自主環境探索、空間表征、路徑規劃、行為決策與目標導航過程[9]。區別于傳統導航技術[10],類腦導航首先要建立類腦機制下的空間表征結果[11],通過類腦認知的方式對空間進行標定,具備類腦路徑整合的能力。網格細胞具有六邊形放電特性,被視為大腦空間定位機制的基礎[12]。
目前,關于網格細胞空間定位機制的3種方案[13]為:① 多尺度網格細胞聯合生成位置細胞[14];② 多尺度網格細胞的空間表征[15];③ 網格細胞放電模式的路徑整合[16]。本文針對網格細胞放電模式路徑整合模型的相關問題進行研究。
Islam等[17]基于頭朝向細胞提出路徑整合模型,該模型采用頭朝向細胞感知運行體的運動方向與運行速度,采用模數計算,將互成60°角的6個頭朝向細胞整合生成類似網格細胞的樣式,并最終實現路徑整合過程。Walters等[18]采用競爭神經網絡與連續吸引子網絡模擬頭朝向細胞,構建基于頭朝向細胞的路徑整合模型。Kubie等[19]基于頭朝向細胞建立了路徑整合模型,通過在探索時記錄訪問點之間的位置,生成“捷徑矩陣”,并在一定范圍內完成了矢量導航任務。3種路徑整合模型均采用頭朝向細胞完成路徑整合,未考慮網格細胞對路徑整合過程的影響,對類腦機制模仿不完整。為實現完整的類腦路徑整合機制,周陽等[20]采用頭朝向細胞模型與網細胞模型分別感知運行體運動的方向與距離,同時引入距離細胞與頭朝向細胞相關聯,最終構建基于頭朝向細胞與網格細胞的路徑整合模型。該模型使用單一尺度的網格細胞模型,由于在曲線運動過程中單一尺度網格細胞只能感知一個位移變化量,路徑整合過程結果存在較大的偶然誤差。
針對以上問題,本文提出一種新型疊加整合算法構建路徑整合模型,該模型由網格細胞與頭朝向細胞共同構成,采用連續吸引子網絡建立網格細胞模型與頭朝向細胞模型,分別感知運行體的運動距離與運行方向。為提高路徑整合過程的準確性,引入多尺度網格細胞模型感知多個位移變化量,采用加權平均法計算最終變化量,優化疊加算法。在運行體的不同運動情況下,靈活改變權重,使路徑整合結果更加精確。
1 模 型
本文采用吸引子網絡建立頭朝向細胞模型與網格細胞模型,提出一種基于新型疊加算法的路徑整合模型。
1.1 頭朝向細胞模型
模型中的旋轉細胞能整合角速度信息,調節旋轉細胞與頭朝向細胞的連接權重,更新頭朝向細胞的放電情況。模型中頭朝向細胞i的放電率[21]為
(1)
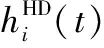
(2)
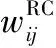
旋轉細胞與頭朝向細胞的連接權重為
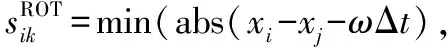
(3)
(4)
式中:ω為頭部角速度。
旋轉細胞與頭朝向細胞之間的連接權重與頭部角速度ω有關。定義“活動包”表示頭朝向細胞活性最大的細胞。根據式(4)可得,當ω>0時,將強化旋轉細胞與順時針方向的頭朝向細胞連接權重,使“活動包”順時針偏移;當ω<0時,將強化旋轉細胞與逆時針方向的頭朝向細胞連接權重,使“活動包”逆時針偏移。因此,頭朝向細胞模型可以實時整合角速度。
1.2 網格細胞模型
本文中采用Burak等提出的單一尺度網格細胞的二維吸引子網絡模型。模型中網格細胞的放電率計算方法[22]為
(5)
式中:f(x)為非線性整流函數,當x>0時,f(x)=x;當x≤0,f(x)=0;si表示神經元i的放電率;Wij為神經元i與神經元j間的連接權值;τ為時間常數;Bi為神經元i的前饋輸入。
模型中設網格細胞模型為二維神經元網絡,為了方便建模,規定每個神經元的優先朝向為(N,S,E,W)中的任意一個(實際中各神經元的優先朝向為連續集合[0,2π]的任意值),該優先朝向由θi決定。如圖1所示,網絡中相鄰的4個神經元的優先朝向各不相同。神經元的優先朝向決定了神經元輸出權重的移動方向與接收速度的大小。
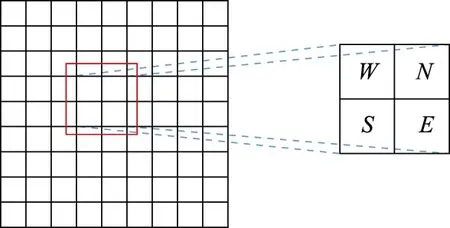
圖1 神經元的優先朝向Fig.1 Preferred direction of neurons
神經元權值矩陣內元素為
(6)
W0=a1e-γmgc|x|2-a2e-βmgc|x|2
(7)
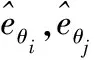
(8)
式中:αmgc為模型速度響應系數;A(xi)為包絡函數,當A(xi)=1,網格細胞網絡為周期性網絡。
1.3 單一尺度網格細胞路徑整合模型
基于單一尺度網格細胞的路徑整合模型通過記錄單個網格細胞的放電次數計算運動距離,根據頭朝向的變化量來判斷運行體是直線運動還是曲線運動。但網格細胞的放電呈現周期性,且放電域在空間中為直線或者近似圓形區域。為了便于距離計算,算法中設置合理放電閾值Hgc,當si≥Hgc時,記網格細胞放電一次,從而使網格細胞的放電域表征空間的一個位置。如圖2所示,運行體位于位置A(或位置B)時,網格細胞放電一次。
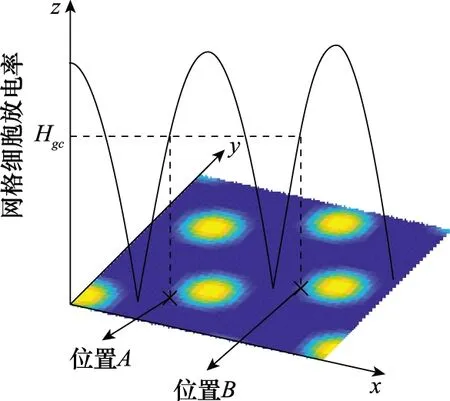
圖2 網格細胞放電率曲線Fig.2 Curve of grid cell firing rate
當前時刻t所處位置A(位置B)即為網格細胞的放電野。為了避免重復計算放電次數,通過設置參數使周期性放電率曲線的上升過程首次出現si≥Hgc時,能夠觸發疊加算法;而同周期內再次出現si≥Hgc時,不再觸發疊加算法。
為區分運行體直線運動過程與曲線運動過程,設置角度閾值與時間閾值。當運行體的頭朝向變化量大于角度閾值時,認為此時進行曲線運動。單一尺度網格細胞模型的距離疊加算法如下:
Δθ=θnow-θsave;(計算頭朝向變化量)
Δt=tnow-tsave;(疊加過程所用時間)
ifsi≥Hgc&& num==1
(放電率上升過程,首次大于Hgc)
num=0;
if Δθ<θth(運行體直線運動);
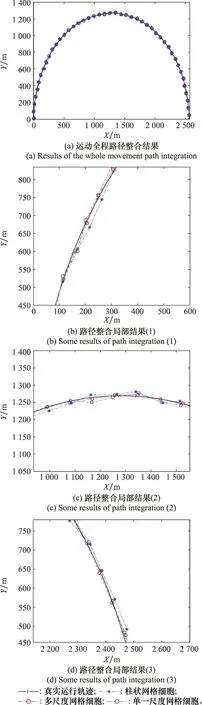
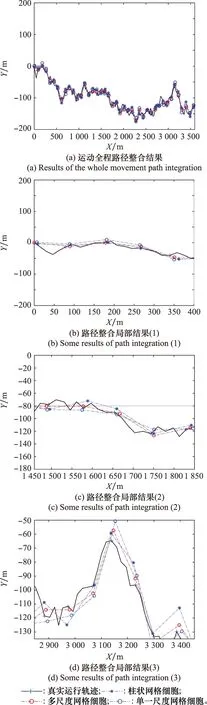
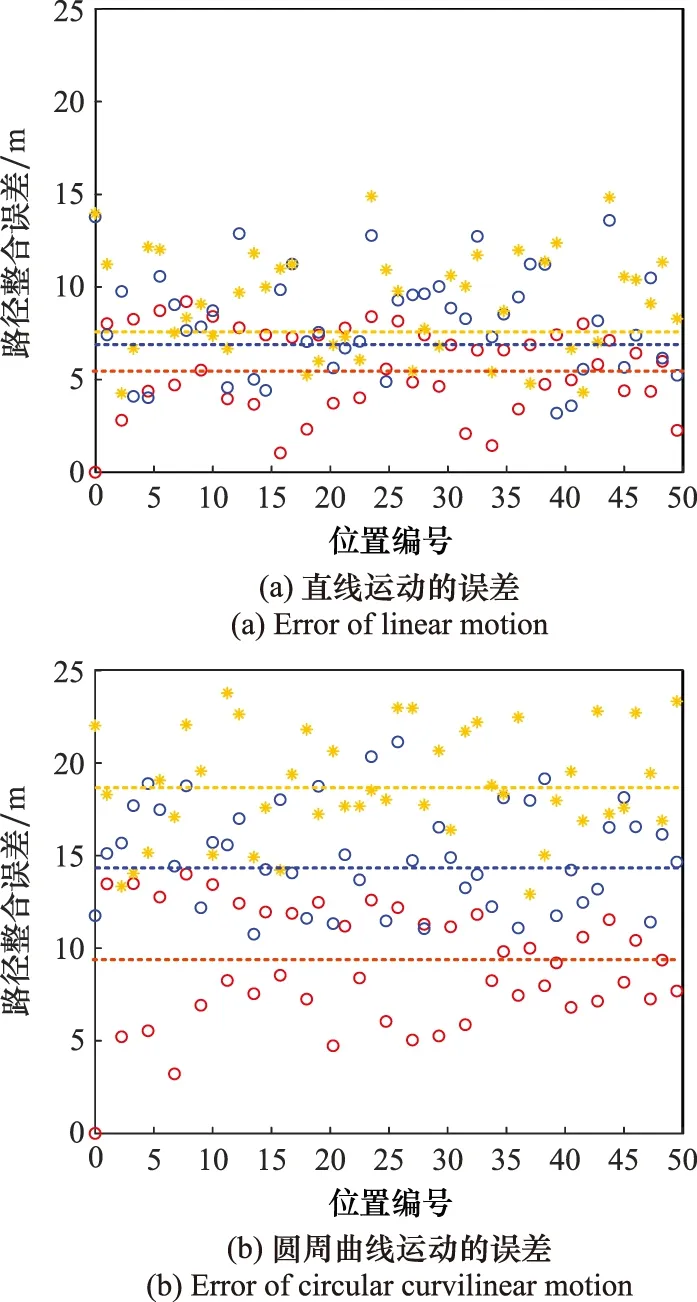
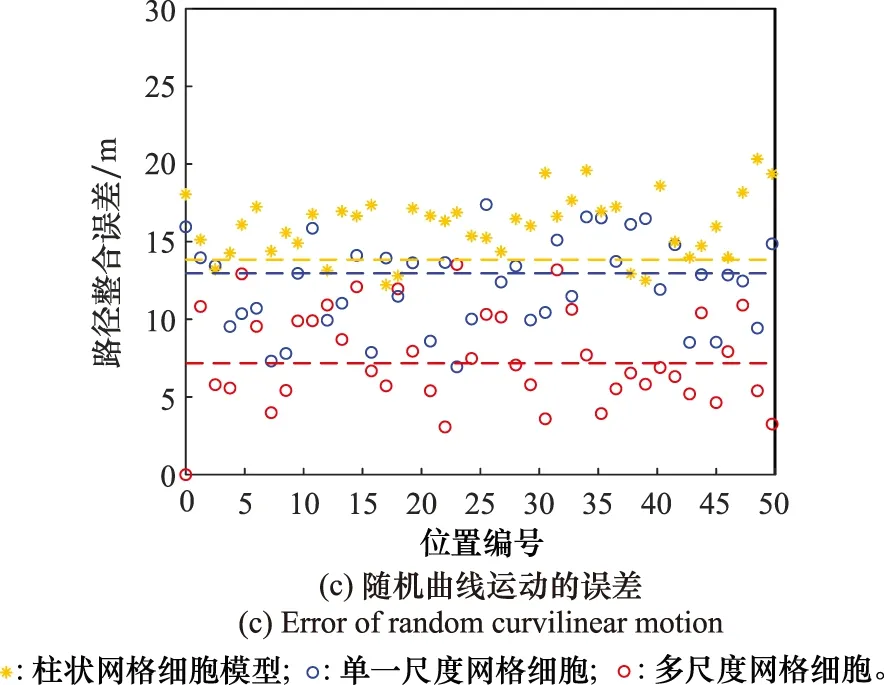
if Δt count=count+1; (記錄網格細胞放電次數) else Δl=count·b; (計算位移的變化量) θsave=θnow,tsave=tnow; (存儲當前頭朝向、時刻) count=0,Δt=0; (重置網格細胞放電次數、時間間隔) end else Δθ≥θth(運行體曲線運動); Δl=count·b; (計算位移的變化量) θsave=θnow,tsave=tnow; (存儲當前頭朝向、時刻) count=0,Δt=0; (重置網格細胞放電次數、時間間隔) end else ifsi (放電率下降過程,首次小于Hgc) num=1; end end 算法中,Δθ為頭朝向變化量;θsave為參考頭朝向;θnow為當前頭朝向;tsave為疊加過程的開始時刻;num為放電率上升沿參數;沿tnow為當前時刻;Δt為疊加過程所用時間;θth角度閾值;Tth為時間閾值;count為網格細胞放電次數;b為網格間距;Δl為位移變化量。 由算法可知,角度閾值θth能夠判斷運行體的運動情況,當Δθ<θth,運行體運動近似為直線運動,當Δθ≥θth時,運行體為曲線運動。當運行體進行曲線運動時,設置合理的θth,使Δθ<θth過程對應的曲線運動等效為直線運動。將曲線運動過程等效為每一小段的直線運動過程,從而完成曲線運動過程的位置計算。 根據單一尺度網格距離疊加算法可知,位移變化量Δl由網格細胞間距b與網格細胞放電次數count決定。而單一網格細胞模型僅通過單個網格細胞的放電率變化計算一次位移變化量,存在較大的偶然誤差。為提高路徑整合模型的精度,本節提出多尺度網格細胞路徑整合模型,調整吸引子網絡模型中的參數γmgc、βmgc,得到不同網格間距的網格細胞群,通過記錄不同網格細胞群中不同網格細胞的放電率變化能分別感知運行體的位移變化量,對所得全部位移變化量加權取平均得到最終的位移變化量,從而減小路徑整合過程的誤差。 多尺度網格細胞模型中,設不同尺度網格細胞得到的位移變化量分別為:Δl1, Δl2, …, Δln;加權疊加所得位移變化量為 Δl=φ1Δl1+φ2Δl2+…+φnΔln (9) 式中:φi為位移權重,0≤φi≤1,且滿足 φ1+φ2+…+φn=1 (10) 根據不同運動情況,位移權重的取值不同。當運行體進行直線運動時,單一尺度網格細胞路徑積分算法可得,不同尺度模型感知的位移變化量基本相同。在此情況下,對所得位移變化量取平均即可得到較為精確的結果。因此設置權重值: φ1=φ2=…=φn=1/n (11) 當運行體進行曲線運動時,由于頭朝向的改變,不同尺度網格細胞的放電次數count不同。由于計數機制大尺度網格細胞模型所得位移變化量的偏差大,小尺度網格細胞模型所得位移變化量的偏差小。因此,需要增大小尺度網格細胞的權重,減小大尺度網格細胞的權重,使最終疊加結果更加精確。本文中取n=5,曲線運動時,φ1=0.5,φ2=0.3,φ3=0.2,φ4=φ5=0。 運行體在運動過程中,模型的接收輸入分別為平移速度與旋轉速度。根據頭朝向細胞的放電情況能夠判斷運行體的運行方向θnow,網格細胞能夠計算得到運行體相對于起始位置的運行距離Δl。因此,當運行體運動一段距離后,路徑整合模型能夠判斷運行體沿著頭朝向方向運行了一段距離,從而實現該過程的路徑整合。通過路徑整合模型得到運行體運動的距離與運行的方向,假設起始位置為a=[x0,y0],通過位置推算得到運行體的運動位置b=[x1,y1]。計算式為 x1=x0+Δlcosθnow (12) y1=y0+Δlsinθnow (13) 將更新后的位置作為新的路徑整合的起始位置,并重復上述步驟,從而實現路徑整合的過程。考慮到完整記錄網格細胞的重復放電以及減少計數誤差,選取在該位置處放電的網格細胞為參考基準,記錄該網格細胞重復放電的次數為運動過程中重復放電的次數,從而減小路徑整合過程的誤差。 為驗證路徑整合模型的性能以及路徑整合結果的誤差,假設網格細胞模型與頭朝向細胞模型感受到的速度不存在誤差。仿真實驗分為直線運動與曲線運動兩個部分,將本文單一尺度路徑整合模型與多尺度網格細胞模型的路徑整合結果與文獻[20]所提模型的結果進行比較,分析本文路徑整合模型的性能。 仿真實驗環境為2 500 m×2 500 m的正方形區域,直線運動過程中,運行體的運動速度為v=5 m/s,旋轉速度為ω=0;曲線運動(本文的曲線運動為勻速圓周運動)過程中,運行體的運動速度為v=5 m/s,旋轉速度為ω=v/r,r=1 250 m。路徑整合模型能夠無差別感知運行體的運動速度,通過網格細胞與頭朝向細胞模型計算位移變化量與頭朝向,并根據式(12)與式(13)完成路徑整合過程。設置驗證路徑整合模型實驗中的一些參數如表1所示。 表1 路徑整合模型仿真參數設置Table 1 Simulation parameter setting of path integration model 如圖3~圖5所示,分別為直線過程與曲線過程的路徑整合結果。對不同原理的路徑整合模型的整合結果進行分析比較,驗證本文方法的先進性。 圖3所示為柱狀網格細胞路徑整合模型[20]與本文模型整合直線運動的結果。真實運動軌跡為運行體以運行速度運行的實際軌跡,準確位置為相應時刻對應的位置,其他位置為推算過程計算所得。根據圖3(a)可知,柱狀網格細胞路徑整合模型(以下簡稱為柱狀模型)、單一尺度網格細胞路徑整合模型(以下簡稱為單一尺度模型)與多尺度網格細胞路徑整合模型(以下簡稱為多尺度模型),都能夠較好的完成直線運動過程的路徑整合。根據圖3(b)可知,通過比較3種模型的路徑整合結果,柱狀模型與單一尺度模型的路徑整合能力相近。與二者相比,多尺度模型的路徑整合結果更加接近運行體的實際位置。直線路徑整合的仿真實驗說明:本文所提的路徑整合模型能夠完成直線運動的路徑整合,且與現有路徑整合模型相比,多尺度網格細胞模型能夠使路徑整合的結果更加準確,提高路徑整合精度,驗證了模型在直線運動中的可行性與先進性。 圖3 直線運動路徑整合結果Fig.3 Results of line motion path integration 圖4所示為柱狀模型與本文模型整合圓周曲線運動的結果。根據圖4(a)可知,柱狀模型、單一尺度模型與多尺度模型都能夠較好的完成曲線運動過程的路徑整合。由圖4(b)~圖4(d)可知,在曲線運動路徑整合過程中,現有柱狀模型的路徑整合誤差較大,本文模型的路徑整合誤差小,且多尺度模型比單一尺度模型的路徑整合結果更接近運行體的實際位置。單一尺度模型與多尺度模型的路徑整合結果都存在一定的誤差,但多尺度模型的誤差維持在更小的水平。 圖4 規則曲線運動路徑整合結果Fig.4 Results of regular curves’ path integration 圖5所示為柱狀模型與本文模型整合隨機曲線運動的結果。根據圖5(a)可知,柱狀模型、單一尺度模型與多尺度模型都能夠較好的完成路徑整合過程。由圖5(b)~圖5(d)可知,在路徑整合的大多數位置處,路徑整合的結果都存在一定的誤差,但總體而言本文路徑整合模型的整合結果要優于柱狀模型,整合誤差維持在更小的水平。 圖5 不規則曲線運動路徑整合結果Fig.5 Results of irregular curves’ path integration 根據圖3~圖5可得,本文路徑整合模型能夠完成直線與曲線運動的路徑整合任務,但不可避免地存在整合誤差。仿真結果表明,直線運動過程,柱狀模型與單一尺度模型的整合誤差相近,都大于多尺度模型;曲線運動過程中,本文模型路徑整合能力都優于柱狀模型,且與單一尺度路徑整合模型相比,多尺度路徑整合模型能夠將路徑整合的誤差保持在更低的范圍內。 對圖3與圖4的路徑整合過程進行誤差分析,得到某些位置的誤差結果如圖6所示。圖6(a)為直線運動過程中某些位置路徑整合的誤差。由圖6可知,隨著運動距離的增加,柱狀模型、單一尺度與多尺度網格細胞路徑整合模型都存在誤差,運動距離小于3 000 m時,柱狀模型與單一尺度網格細胞模型的誤差為12 m左右,而多尺度網格細胞模型的誤差基本維持在10 m之內。因此,直線運動過程中多尺度路徑整合模型的誤差小于柱狀模型與單一尺度路徑整合模型。圖6(b)為曲線運動過程中某些位置路徑整合誤差。由圖可知,運行體在曲線運動距離約3 000 m的過程中,柱狀模型的路徑整合模型累計誤差在15~25 m,單一尺度網格細胞路徑整合模型的累計誤差在10~20 m,多尺度網格細胞路徑整合模型的累計誤差在8~14 m。圖6(c)為隨機曲線運動過程中某些位置路徑整合誤差,由圖可知,柱狀模型的累計誤差在10~20 m,單一尺度模型的累計誤差在8~17 m,多尺度路徑整合模型的累計誤差在4~12 m。因此,曲線運動過程中本文所提模型(單一尺度路徑整合模型與多尺度路徑整合模型)的誤差小于柱狀路徑整合模型。 圖6 路徑整合的誤差Fig.6 Error of path integration 綜上可得,本文路徑整合模型能完成路徑整合任務。直線運動過程中,單一尺度網格細胞路徑整合模型與柱狀網格細胞模型的誤差相近,都大于多尺度網格細胞模型。曲線運動過程中,與柱狀模型相比,本文模型(單一尺度模型與多尺度模型)的誤差更小。因此,本文所提多尺度網格細胞在直線與曲線運動中路徑整合的誤差更小,整合結果更精確,具有可行性與先進性。 本文主要解決了類腦導航機制中使用多尺度網格細胞與頭朝向細胞完成路徑整合的問題。提出了一種基于新型疊加算法的路徑整合模型,并結合多尺度網格細胞優化了疊加算法。通過仿真驗證了算法的有效性,證明了多尺度路徑整合模型的性能優于單一尺度模型。但實現類腦導航除了使用類腦機制完成路徑整合過程外,還需要結合外部傳感器優化路徑整合過程,建立更加準確的類腦機制下的空間表征。因此,為實現類腦導航,需要結合視覺傳感器等進行更進一步的研究。1.4 多尺度網格細胞路徑整合模型
2 仿真實驗及分析
2.1 仿真實驗參數設置
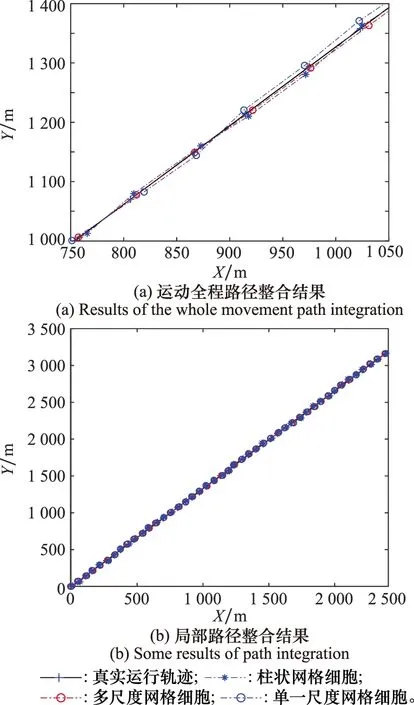
2.2 仿真實驗結果分析
3 結 論

