基于雙目視覺的空中加油錐套定位與對接控制

張易明, 艾劍良

(復旦大學航空航天系, 上海 200433)

0 引 言

空中加油是一種增加無人作戰飛機作戰半徑的主要方法,可分為軟管-錐套式(軟式)、伸縮套管式(硬式)兩類[1]。其中,采用軟式加油系統進行空中加油具有加油裝置體積小、結構簡單、便于拆裝、可在一臺加油機上安裝數套裝備等優勢[2],有廣闊的應用前景。空中加油過程包括會合、編隊、對接、加油和退出5個階段,對軟式自主空中加油而言,對接階段對控制的要求最高[3]。在軟式加油過程中,加油錐套在加油機尾渦下洗及大氣紊流作用下處于持續運動中[4],其擺動范圍可達到2 m[5]。因此,快速準確地定位錐套位置,是實現自主精確對接控制的前提條件。

在對接過程中,受油機從加油機側后方鎖定加油錐套并逐漸靠近。在這個區域,由于多種干擾影響,傳統慣性導航與GPS組合的導航方法難以提供高精度的位置測量信息[6],而使用雷達系統難以從加油機-加油裝置組合體中分辨出加油錐套的位置。因此,基于視覺技術的測量方法是具有應用潛力的方案之一。近年來,相繼出現了一些基于Mean-Shift和卡爾曼濾波及其改進或結合形式的單目錐套檢測方法[7-12],用于從攝像機拍攝到的圖像中尋找加油錐套。在對接過程中,僅在相機視野中識別出加油錐套是不夠的,還需通過測量錐套在視場中的深度解算其空間位置。文獻[13-14]開展了基于雙目視覺的加油錐套定位研究,文獻[15-17]研究了基于深度學習的錐套定位方法。對于雙目立體視覺問題,傳統的方法是先在一側畫面中提取感興趣的點或區域,利用色彩/灰度匹配邊緣匹配等方法在另一側畫面中找到共軛點對,隨后通過對極幾何求解空間點的坐標信息[18]。此種方法計算量大,難以滿足實時性要求。考慮到加油錐套在受油機視野中的幾何形態相對簡單且固定,可利用基于深度學習的目標檢測網絡分別在兩側畫面中定位其中心位置,再利用對極幾何求解其空間坐標,可加快對加油錐套定位的速度。

對于圖像中錐套目標的檢測問題,多數研究是基于色彩信息的濾波跟蹤方法,需要在加油錐套上額外加裝彩色光源以區分前景與背景,并要求加油錐套在受油機視野中呈現完整的橢圓形。當跟蹤目標與背景顏色接近或被遮擋時,容易出現跟蹤窗口擴大等問題;同時,此類方法對初始幀中目標所在位置的估計有較大依賴。為克服以上問題,可以引入深度學習網絡用于圖像中的目標檢測。YOLO(you look only once)系列是一種高速的目標檢測網絡[18-22],它的優勢是兼顧了推理精度和速度,可作為目標檢測階段的一種選擇。

在可獲得錐套空間坐標的前提下,自主空中加油的對接控制問題可分為三部分:指令項、跟蹤項、鎮定項。指令項即指從編隊位置到對接位置的參考軌跡設計。通常參考軌跡被設計為一條平滑軌跡,以避免過度的超調和震蕩。現有的研究主要采用低通濾波器[23]、多項式[24]等方法生成參考軌跡等方法。跟蹤項(外環)使受油機按照指定的參考軌跡完成對接任務,一般可以構建誤差系統將跟蹤問題轉換為鎮定問題。常見的方法有:非零點集方法(non-zero setpoint,NZSP),該方法將參考輸出轉化為參考狀態[25];隨后有學者提出指令生成跟蹤器方法(command generator tracker,CGT),以克服NZSP需要常值參考輸出的缺點[26]。鎮定項(內環)用以保證系統穩定和收斂,基于比例-積分-微分(proportion integral derivative,PID)[27]和線性二次型調節器(linear quadratic regulator,LQR)[28-29]的控制器是比較常見的方法,亦有學者開展了基于自適應控制[30]、反步法[31-33]的對接控制研究。

1 問題描述

在空中加油對接階段,受油機起始位置一般位于加油錐套側后方偏下位置。以受油機機體系為參考坐標系,定義加油錐套中心相對受油機的位置矢量為rd=(xd,yd,zd),如圖1所示。完成自主對接控制的任務即可分解為:第一,實時獲得錐套位置rd;第二,使rd在一定時間內趨于0。

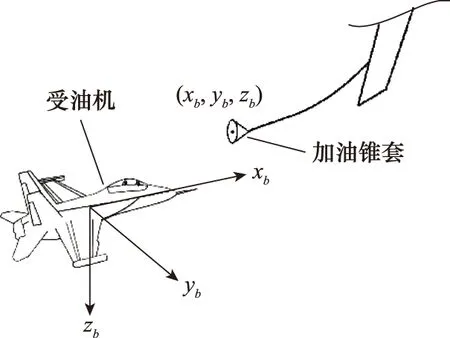
圖1 受油機機體坐標系Fig.1 Body-axes of receiver aircraft

為實現上述目標,實現自主對接的任務流程可歸結如下。

步驟 1利用計算機視覺方法獲得rd:

(1) 在相機成像畫面中檢測加油錐套所在位置;

(2) 利用相機成像的映射關系反推加油錐套的空間位置rd。

步驟 2規劃一條平滑的參考軌跡,在指定時間內逐漸消除rd。

步驟 3設計控制率使受油機跟蹤參考軌跡以完成對接任務。

2 基于雙目視覺系統的錐套定位

在受油機上架設雙目相機后,在機體系內獲得rd的問題轉化為求取錐套在相機系統內的空間坐標問題。在實際應用中,單個相機捕獲的是二維圖像。因此,需求解空間點與相機成像畫面點間的映射關系,進而獲得加油錐套的空間坐標。

2.1 相機成像模型

相機成像過程涉及如下坐標系:

世界坐標系Ow-xwywzw,描述相機及被攝物體在真實物理空間中的位置,其原點和坐標軸方向可以任意指定,單位為mm;

相機坐標系Oc-xcyczc,其原點位于鏡頭光學中心,xc,yc軸與成像畫面的兩條邊平行,zc軸與鏡頭光軸重合,單位為mm;

像素坐標系Opix-xpixypix,原點為成像畫面左上角,xpix,ypix軸分別與成像畫面的兩條邊平行,該坐標系反應成像畫面中每一個像素點的行、列位置,坐標值均為非零正整數,單位為pixel。

圖像坐標系Oimg-ximgyimg,原點為成像平面中心,ximg、yimg軸分別與成像畫面的兩條邊平行,單位通常與世界坐標系一致。圖像坐標系是對像素坐標系的物理性補充,便于參與相機坐標系及世界坐標系間的坐標變換。以上坐標系間關系如圖2所示。

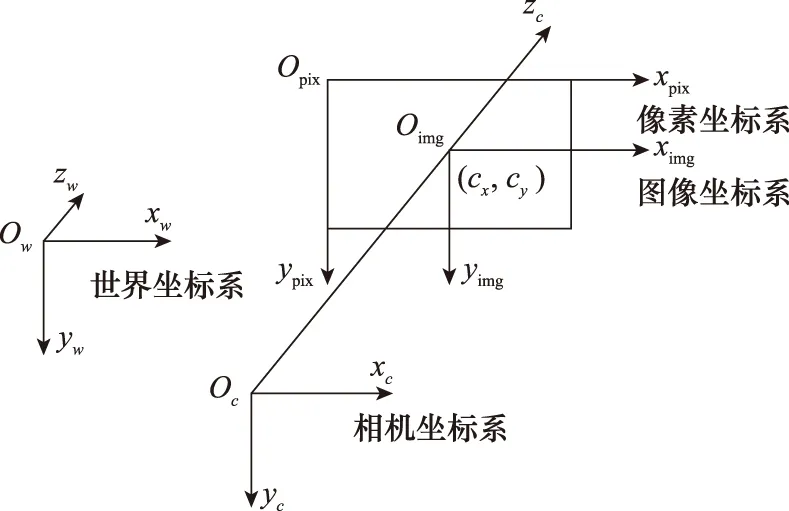
圖2 世界、相機、圖像和像素坐標系Fig.2 World, camera, image and pixel coordinates

相機成像模型可表示為

(1)

式中:KInt為內部參數矩陣;MExt為外部參數矩陣;zc稱為尺度因子。具體表示為

(2)

式中:fx,fy分別為x、y方向對應的等效焦距,其定義是物理焦距與單位像素寬度的比值,單位為pixel;(cx,cy)為Oimg在Opix-xpixypix系下的坐標。

KExt=[R,t]

(3)

式中:R為3×3正交旋轉矩陣;t為3×1平移向量。

實際的相機成像過程還需考慮鏡頭畸變,數學表達為

(4)

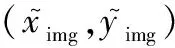
式(1)～式(4)描述了空間點(xw,yw,zw)到像素平面成像點(xpix,ypix)的映射關系,求解KInt、MExt、k、p的過程稱為相機標定,可使用張正友標定法進行相機的參數標定[34]。張正友標定法是一種通過匹配棋盤格圖像上角點的真實坐標與其成像坐標來求解成像映射關系的方法,主要步驟為[35]。

步驟 1令zw=0平面與棋盤格平面重合,構造單應性矩陣,求解內參矩陣;

步驟 2利用R的單位正交性求解外參矩陣;

步驟 3求解鏡頭畸變參數;

步驟 4用LM(Levenberg-Marquardt)方法[36]優化標定結果,使平均重投影誤差極小。

2.2 基于平行雙目相機的空間點定位

假設一對雙目相機滿足如下關系(以下簡稱“理想雙目系統”):

① 內參相同；② 光軸平行；③ 左右成像平面共面；④ 對極線行對齊。則可根據相似三角形原理求解空間一點到相機平面的距離,如圖3所示。

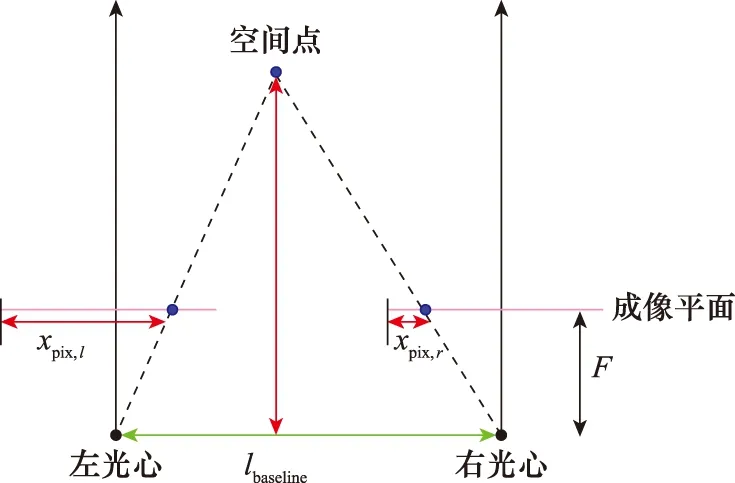
圖3 平行雙目相機測距Fig.3 Distance measurement with parallel cameras

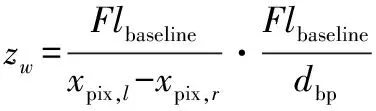
(5)

式中:lbaseline為兩相機光心距離,稱為基線;dbp=xpix,l-xpix,r為左右兩成像平面內成像點的視差;F為焦距。

令世界系與其中一相機系重合(如左相機),則不難計算得到:

(6)

式(6)表明,當雙目相機系統滿足理想雙目系統假設,空間點坐標可由其成像的像素坐標、相機內部參數及兩相機間基線長度確定。

由于實際雙目系統可能存在加工或安裝誤差,需進行立體校正,使其變換為理想雙目系統。

首先求解兩相機間的實際相對關系。空間一點P坐標(xw,yw,zw)在一組雙目相機各自的相機系下坐標有如下關系:

(7)

對n張標定板進行標定,則可由n次標定獲得的相機外參Rr、tr、Rl、tl求得兩相機間的旋轉、平移關系為

(8)

式中:Rrl、trl分別為左相機向右相機系的旋轉矩陣、平移向量。

為將雙目系統變換為理想系統,可進行如下操作:

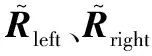
(9)

步驟 2構造Rrect=[e1,e2,e3]T使極點落于無窮遠處。令e1與trl,e2與主光軸正交,e1、e2、e3正交,則有:

(10)

步驟 3構造校正矩陣:

(11)

對兩相機捕獲的圖像分別左乘式(11),即可得到校正后的理想雙目系統成像。

假設雙目系統左相機光軸與受油機體軸Obxb平行,其光心在受油機機體坐標系系內位置矢量為rbc則加油錐套位置矢量可表示為

(12)

2.3 目標檢測網絡

在標定雙目相機系統后,還需獲得加油錐套中心在成像平面內的像素坐標(xpix,ypix),即可利用式(12)求得加油錐套中心在雙目相機系統坐標系內的坐標。本文采用一種基于改進YOLOv4-Tiny的目標檢測網絡獲得加油錐套中心在圖像中的像素坐標。

YOLOv4系列網絡在Neck部分采用了FPN(feature pyramid networks)+PAN(path aggregation network)的結構進行特征融合。其中,FPN結構能給增強high-level語義,有利于完成分類任務;PAN能增強low-level語義,有利于完成定位任務[37]。YOLOv4-Tiny是YOLOv4的輕量化版本,它犧牲了一定的精確性,但檢測速度更快,更適合完成實時檢測任務。

2.3.1 網絡結構

YOLOv4-Tiny的網絡結構如圖4所示。圖中,Conv表示卷積層,Leaky表示Leaky ReLU激活函數,Linear表示Linear激活函數,BN表示batch normalization層[35]。

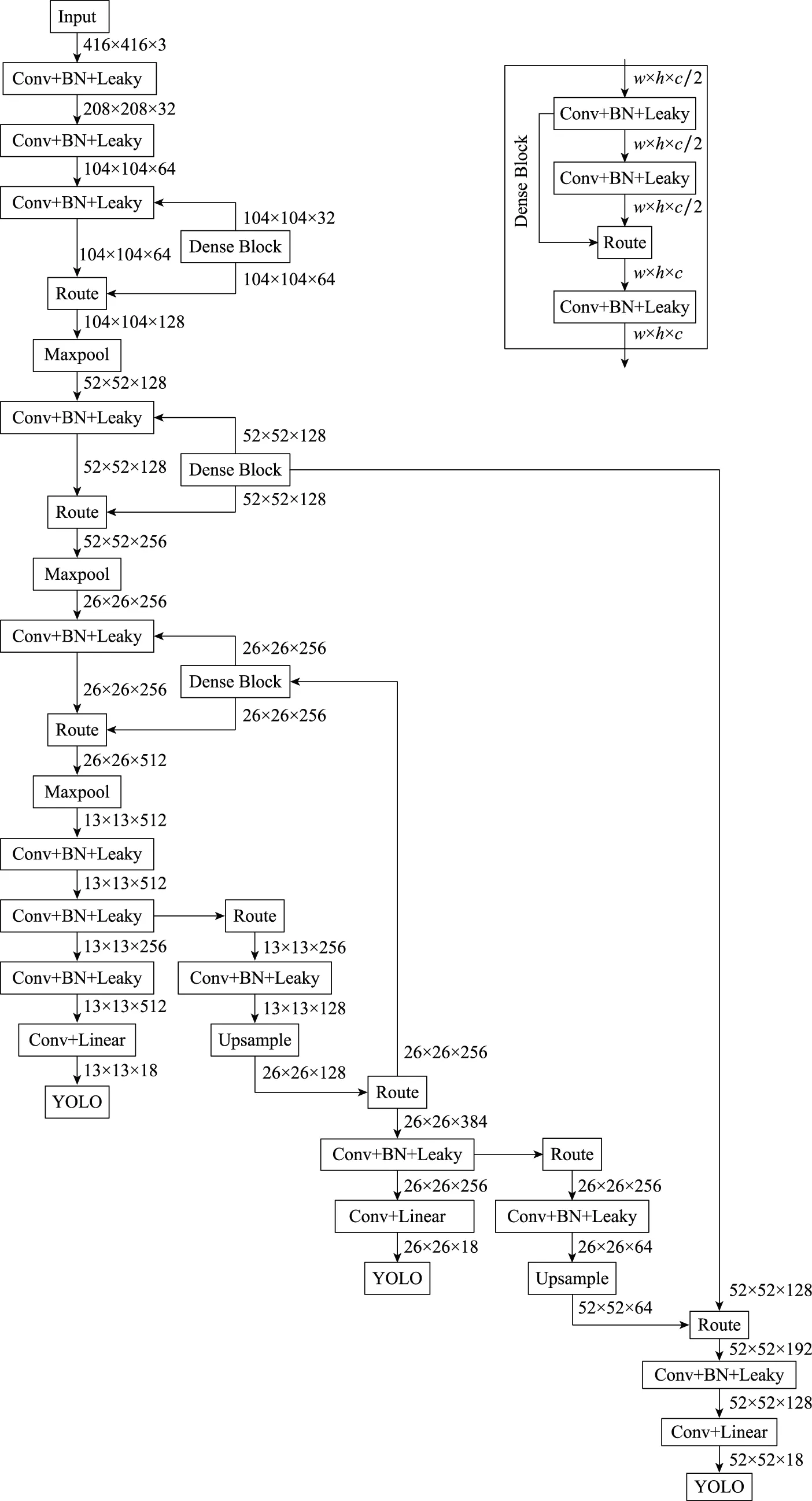
圖4 YOLOv4-Tiny結構Fig.4 Structure of YOLOv4-Tiny

分析網絡結構不難發現,每個YOLO層前的Conv+BN+Leaky層占用較多計算資源。以第一個YOLO層前為例,其卷積層尺度為3×3×512,輸入256個特征圖,需1 179 648個參數。參考network in network (NIN)方法[38],將一個3×3×512的卷積層分解為3個:1×1×128→3×3×128→1×1×512,可在實現原卷積層功能的同時,將參數減少到245 760個。對3個YOLO層前的Conv+BN+Leaky層做同樣處理。

其次為增加降采樣階段的感受野,在第一個Dense Block中插入空間金字塔池化(spatial pyramid pooling, SPP)模塊,如圖5所示。

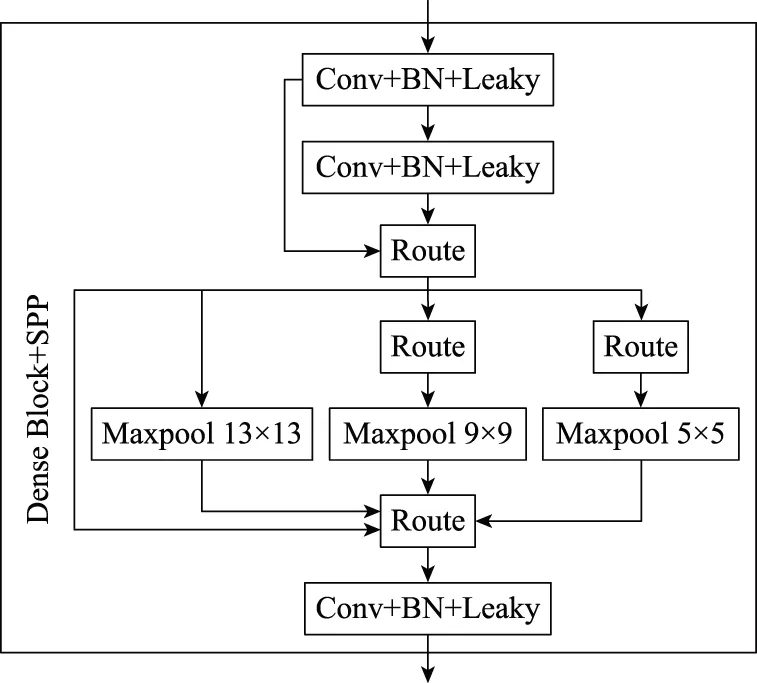
圖5 在Dense Block中插入SPPFig.5 Insert SPP into Dense Block

經過如上兩項修改的網絡在下文中稱為YOLOv4-TSPP。

2.3.2 網絡輸出

網絡的輸出為目標類別、分類置信度、目標邊界框。目標邊界框有4個待預測參數:(tx,ty,tw,th),如圖6所示。其中,(tx,ty)為邊界框中心的偏移量,(tw,th)為寬高縮放比。(bx,by,bw,bh)為預測得到的目標邊界框,其中

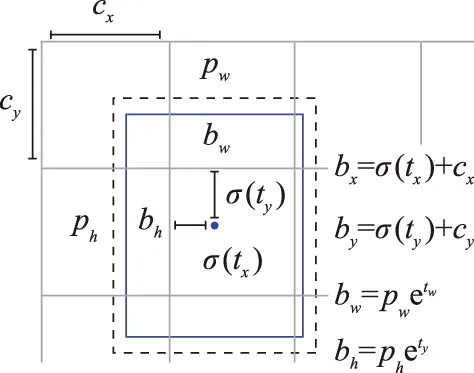
圖6 邊界框的預測Fig.6 Prediction of Bounding-Box

(13)

是邊界框中心相對圖像左上角的偏移量;

bw=pwetw,bh=phety

(14)

是邊界框的寬和高;(cx,cy)是預設邊界框在特征圖上的中心坐標;(pw,ph)是預設邊界框在特征圖上的寬和高。

2.4 加油錐套橢圓擬合

近距離對接過程中,受油機需要將受油插頭插入加油錐套中。前節建立的檢測網絡在理想狀態下輸出一個外接于錐套的矩形框。實際加油錐套在受油機視野中為圓形,在外接矩形所框定的范圍內存在非插入目標區域,若受油機錯誤進入該區域則可能導致對接失敗。為此,本文在獲得預測矩形框的基礎上建立一種“向心八點法”快速擬合錐套邊界。首先作如下假設:

(1) Yolov4-TSPP已經提供了相當高交并比的外接矩形框;

(2) 加油錐套末端的穩定傘色彩沿其周向基本保持一致;

(3) 在近距離對接時,預測矩形框內大部分被錐套占據,剩余部分幾乎為顏色一致的天空。

基于以上假設,建立如下橢圓邊界擬合流程:

步驟 1裁剪畫面,只保留矩形框內的區域;

步驟 2用Otsu方法將裁剪出的區域二值化處理[39],矩形框四個角點處應全為0或全為1;

步驟 3從矩形框的4個角點出發,各沿兩條直線搜索錐套橢圓邊界上的點,共尋找8個邊緣點用于擬合橢圓;

步驟 4利用最小二乘法擬合出橢圓。

邊緣點搜索的方法見圖7,以右上角出發為例,分為圖示兩條路徑。二值化后黑色像素為目標邊緣,值為1;白色像素為背景,值為0。搜索目標為在直線路徑上找到離矩形框角點最近的目標邊緣點。

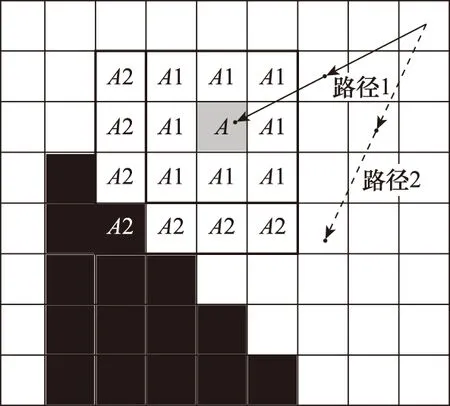
圖7 邊緣檢測方法Fig.7 Method of edge detection

為了過濾孤立噪聲點,當前點A處為1時,檢查其周圍3×3范圍內A1的值是否全為1或大部分為1(如和為8),若是則進一步沿搜索方向取4×4范圍內A2值是否全為1,或A,A1,A2的像素點集合大部分為1(如和為14)。若滿足上述條件,則判斷當前像素點A為邊緣點。對8條路徑重復上述步驟,即可得到落于錐套橢圓邊界上的8個點。

相比在全局范圍內進行邊緣檢測,“向心八點法”的計算量極小,只需在Yolov4-SPP給出的矩形框內進行8次一維搜索,即可得到加油錐套橢圓形邊界。針對具體情況可對此方法進行更詳細地邏輯梳理,例如:當二值圖內存在一個矩形框角點與其他角點非同值,則可只取6個點進行橢圓擬合;當二值圖內存在2個角點與另外2個角點非同值,可根據過去幾幀預測的矩形框適當調整裁剪范圍等。

2.5 加油錐套實時定位流程

結合第2.1節～第2.4節所述方法,可針對實時獲取加油錐套位置及擬合其橢圓邊緣這一任務目標建立一套完整的工作流程。總結為圖8。

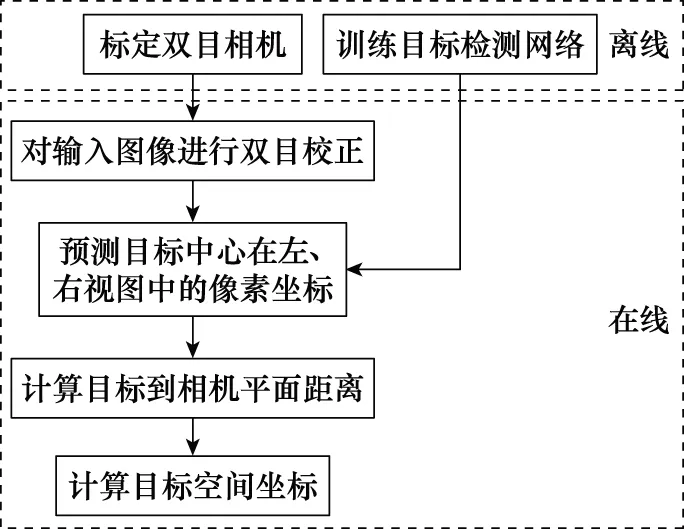
圖8 錐套定位流程Fig.8 Scheme of drogue positioning

3 受油機自動對接控制律設計

前文已討論了一種由固連于受油機上的雙目相機獲取加油錐套相對機體位置的方法,因此選擇受油機機體坐標系進行動力學建模及控制律設計。

3.1 受油機模型

機體坐標系下受油機線性化模型定義為

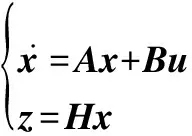
(15)

3.2 參考軌跡設計

為了避免過大的超調,引入時間t的7次多項式函數作為參考軌跡,引導受油機接近加油錐套完成對接任務,其形式為

ηr(t)=fT(t)Aco

(16)

式中:ηr=(xr,yr,zr)為位置指令;f(t)=(t4,t5,t6,t7);Aco=[ax,ay,az]為系數矩陣。參考指令可做如下設計。

對齊階段,在時間段[0,t1]消除y,z方向的初始位置偏差(yd0,zd0):

(17)

(18)

精確跟蹤階段,在時間段[t1,t2]進行指令過渡,在時間段[t2,tf]完全跟蹤錐套位置,具體地:

(19)

式中:(Δydrogue(t),Δzdrogue(t))為加油錐套相對初始位置的位移;kr(t)為過渡函數,定義為

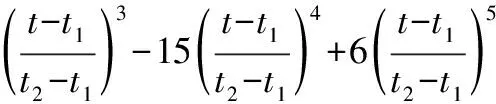
(20)

式(20)的引入可令參考軌跡指令在全任務時間內實現由7次多項式逼近向完全跟蹤的平滑過渡,避免指令切換引起的震蕩。

在x方向,加油錐套的運動幾乎可以忽略不計,設計參考軌跡為

xr(t)=f(t)ax

(21)

由以下終端條件可求得系數向量ax為

(22)

式中:vf為對接時受油機相對加油錐套的前向速度,通常為0.5 m/s左右。

3.3 基于RSLQR増廣的模型參考自適應控制

對理想系統,定義跟蹤誤差為

e=zd-z

(23)

為消除跟蹤誤差,引入積分信號:

(24)

將式(23)、式(24)代入式(15)得:

(25)

增廣的系統動力學方程為

(26)

引入增廣系統的狀態量及系統矩陣,可將式(26)記為

(27)

基準控制量設計為增廣狀態的負反饋形式:

ub l=-Kxx+KceI

(28)

引入線性二次型指標:

(29)

式中:Q=diag(Q1,Q2);R為正定矩陣。引入代數Riccatti方程:

PA+ATP-PBR-1BTP+Q=0

(30)

則反饋增益為:

KLQR=[Kx,-Kc]=R-1BTP

(31)

為提供控制系統魯棒性,可在基準控制器的基礎上引入自適應控制量。考慮帶有不確定性的 無人機開環系統模型為

(32)

式中:Λ表征控制系統的潛在缺陷;ΘT表征系統匹配不確定性;Φx為部分狀態量。定義參考模型為

(33)

定義系統對參考模型的跟蹤誤差為

eref=xe-xref

(34)

總控制輸入為

(35)

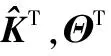
(36)

(37)

式中:proj(θ,y)為投影算子,其定義為

(38)

f為θ的凸函數,定義為

(39)

受油機對接控制系統的示意圖如圖9所示。

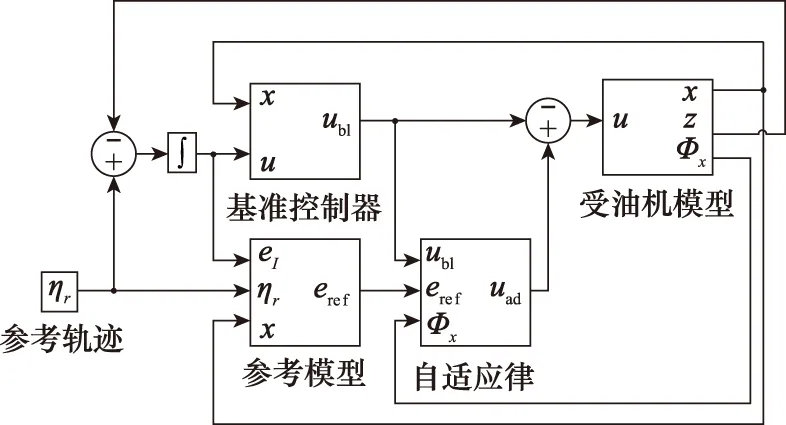
圖9 對接控制系統框圖Fig.9 Diagram of docking controller system

4 實驗方法與結果

4.1 實驗環境

雙目相機系統由兩臺同型號相機平行架設而成;計算機為單GPU的單人電腦;標定用棋盤格采用硬質PET材質制作,棋盤格邊框為6 mm,并增加背光,以提高圖像對比度。具體環境如表1所示。

表1 實驗環境Table 1 Experiment environment

4.2 雙目視覺系統驗證實驗

4.2.1 雙目相機標定

拍攝15組棋盤格圖像,利用張正友標定法分別對兩相機標定內、外參矩陣,計算重投影誤差,如圖10所示。圖10中,對15組標定板進行重投影,其平均重投影誤差為0.51 pixels,實驗中輸入圖像大小為2 592×1 936 pixels,單張圖片的最大平均重投影誤差為1.17 pixels,為圖片對角線長度的0.036%,可見標定結果可靠。

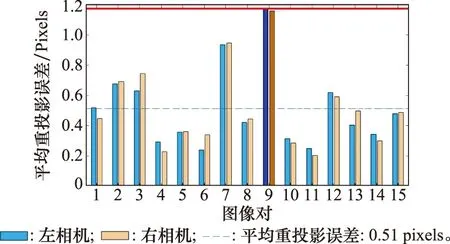
圖10 重投影誤差Fig.10 Reprojection error

經標定得到兩相機內部參數如下。

(1) 左相機

焦距Fl=2.373 5×103

光心(cx,cy)l=(1 297,969)

徑向畸變kl=[0.4 101,-1.9 595,3.2 949]T

切向畸變pl=[-0.023 5,0.001 7]T

(2) 右相機

焦距Fr=3.446 3×103

光心(cx,cy)r=(1 297,969)

徑向畸變kr=[0.377 6,-1.5 757,2.8 951]T

切向畸變pr=[-0.014 3,0.008 1]T

右相機相對左相機的旋轉矩陣、平移向量為

trl=[-115.416 7,-0.856 3,-0.817 0]T

以左相機光心為世界坐標系原點,兩相機及所拍攝標定板在世界坐標系的位置如圖11所示。

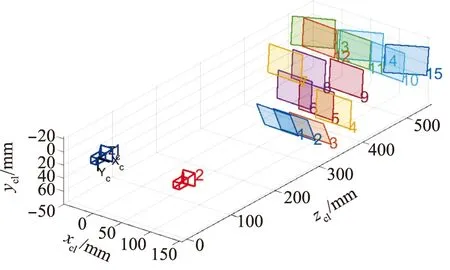
圖11 相機及標定板的位置Fig.11 Location of cameras and checkboards

4.2.2 目標檢測網絡訓練及測試

在單GPU計算機訓練訓檢測網絡,使用同樣的訓練參數對YOLOv4、YOLOv4-Tiny及YOLOv4-TSPP進行訓練,參數設置如表2所示。

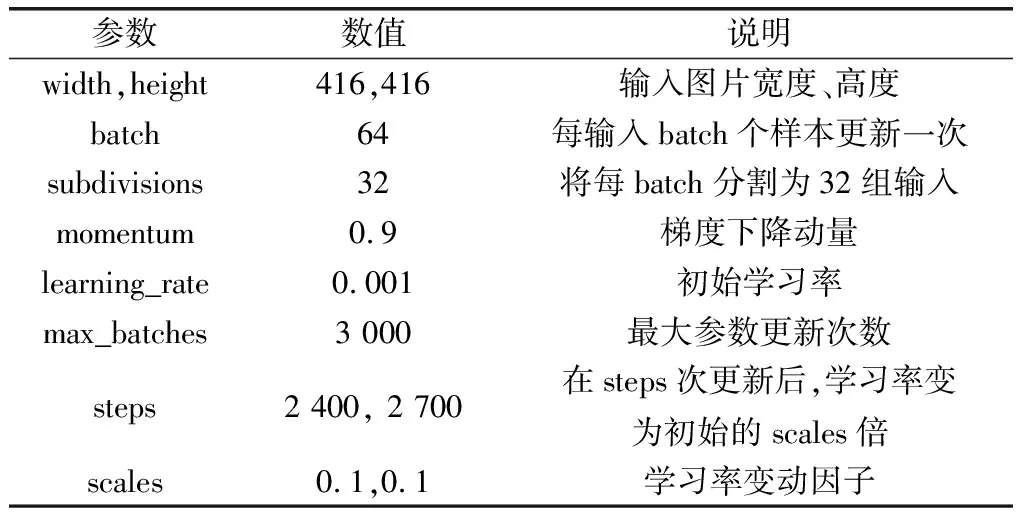
表2 訓練參數Table 2 Training parameters

對數據集作如下說明。

訓練集:由2 000張加油錐套縮比模型(約1∶12.5)的照片構成。為增加樣本多樣性并提高網絡分類能力,針對加油錐套多空洞結構的特點,訓練集圖片具有以下特征:① 畫面內存在多種不同背景,部分背景與錐套模型顏色相近;② 錐套模型存在尺寸、姿態、位置變化、部分超出畫面等情況;③ 存在其他與錐套模型具有相似尺寸的圓形物體。圖12是訓練集部分圖片示例。

圖12 訓練集示例Fig.12 Examples of training set

測試集:150幅由視頻生成的連續圖片序列,對其進行人工標注。測試集與訓練集相互獨立,且背景中存在干擾物。

(1) 目標檢測網絡性能測試

利用以上數據集按表2參數訓練YOLOv4、YOLOv4-Tiny及改進的YOLOv4-TSPP,在測試集上的測試結果如表3所示。與YOLOv4-Tiny對比,YOLOv4-TSPP的卷積層浮點運算量為降低為73.51%,模型權重文件尺寸降低為69.53%;檢測速度下降了9.14%,但仍然高達182 FPS,足以滿足實時性要求;目標邊界框預測值相對真值的平均IoU提高了5個百分點,達到88.53%,這意味著網絡可以較好地預測目標所在位置及其大小。

表3 檢測網絡在測試集上的性能對比Table 3 Performance comparison of detectors running on test set

在測試集上比了YOLOv4-TSPP與傳統方法(文獻[11],Camshift+卡爾曼濾波)的目標檢測性能。圖13顯示,YOLOv4-TSPP能精確預測目標中心;使用Camshif方法時在部分時間段出現了嚴重的漂移,其原因在于邊界框預測隨著時間的推移出現擴大的情況,當聚類信息強于目標的干擾物進入預測框時,干擾物被錯認為目標。

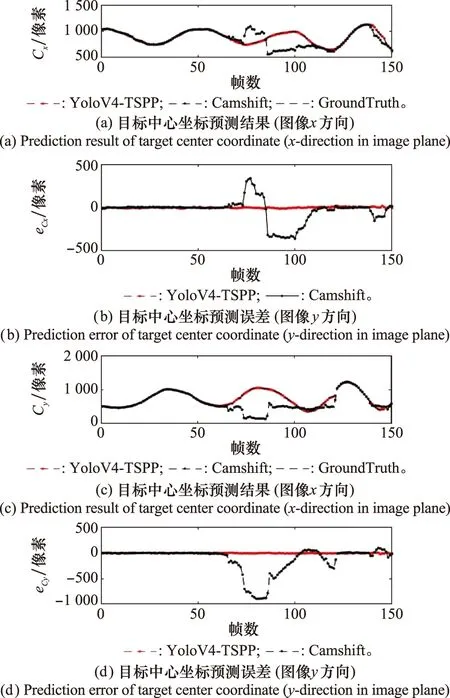
圖13 圖像序列預測Fig.13 Predictions on image sequence

圖14統計了預測框與目標外接框真值的交并比(intersection over union, IoU),YOLOv4-TSP的預測維持了較高的IoU,而Camshift無法維持良好的預測。

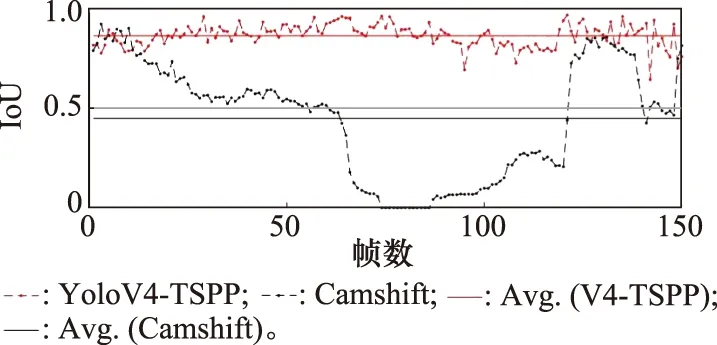
圖14 圖像序列IoUFig.14 IoU on image sequence

(2) 雙目定位試驗

用已標定雙目相機拍攝若干組包含錐套模型的圖像對,每組間目標沿相機光軸方向間隔50 mm,離相機的350～2 000 mm(縮比模型直徑約為真實加油錐套的1/12.5,相當于驗證了雙目系統在距離4～25 m范圍內的預測真實錐套位置的能力)。

先用YOLOv4-TSPP分別預測目標中心在左、右相機畫面內的像素坐標,再利用式(6)即可求解其空間坐標。在此流程中,目標的空間定位誤差主要來源于深度zw的測量誤差,在相機標定足夠精確的前提下,由式(6)通過zw求解xw、yw的過程不引入額外誤差,因此應主要針對深度測量開展試驗。

圖15 雙目目標檢測試驗(經立體校正)Fig.15 Test of binocular object detection (stereo rectified)

試驗對比了對輸入的雙目圖像進行校正及未進行校正的情況,試驗結果表明:

(1) 進行雙目校正有助于提升測距精度,距離預測的平均誤差分別為:校正后-0.110 2 mm,未校正17.912 2 mm;定義距離的相對預測誤差為絕對誤差與實際距離的比值,可得每組測距的相對誤差,如圖16所示。

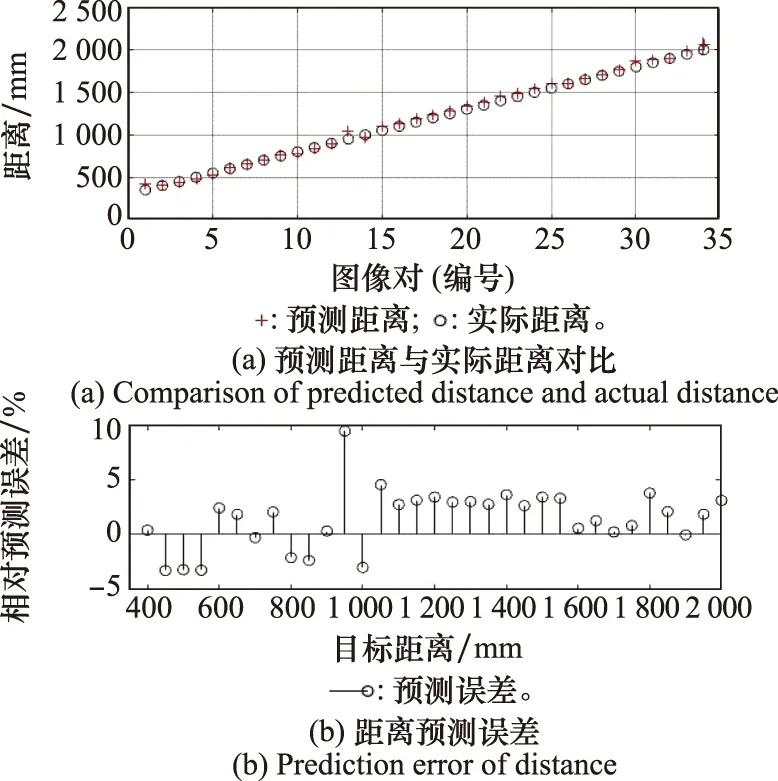
圖16 距離預測結果Fig.16 Result of distance prediction

(2) 左、右兩視圖中目標中心的連線應落在同一水平線上。進行雙目校正后,預測目標中心點對連線相對水平線的平均偏角為-0.230 7°,不進行雙目校正,其平均偏角為-0.692 0°。這從側面說明,該方法在避免進行全局水平匹配搜索的情況下,依然能夠很好地預測目標中心位置。目標中心點對的連線相對水平線的偏角情況如圖17所示。

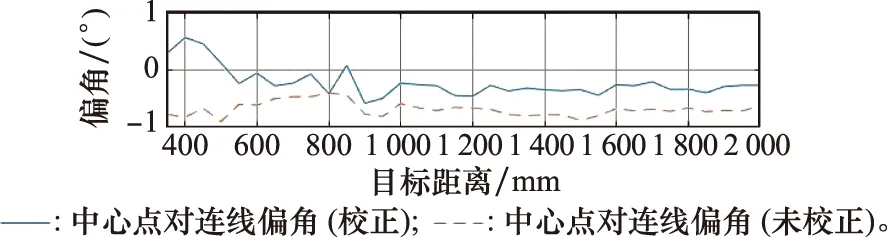
圖17 預測中心連線相對水平線的偏角Fig.17 Deflection angle of connecting line between predicted centers over relative to horizontal line

圖18展示了雙目系統預測目標位置的結果,圖中實際位置為試驗過程中錐套模型擺放位置的近似空間軌跡,在深度預測具備足夠精度的前提下,可以認為空間位置預測亦具備足夠精度。

圖18 目標在世界坐標系中的位置Fig.18 Location of target in world coordinates

(3) 橢圓擬合試驗

對輸入圖像由Yolov4-TSPP在測試集上預測的矩形框后,利用第2.4節提出的向心八點法擬合得到錐套邊緣。橢圓擬合的結果如圖19所示,在測試集上搜索得到8個邊緣點并進行橢圓擬合的平均耗時約為0.015 s(Matlab環境)。

圖19 橢圓擬合效果Fig.19 Performance of ellipse fitting

4.3 對接控制系統仿真實驗

第4.2節表明,基于YOLOv4-TSPP的雙目系統可以有效捕捉加油錐套相對受油機的位置,因此,可基于此前提,采用文獻[33]給出的狀態空間模型對加油錐套運動進行仿真,并仿真驗證對接控制器的性能。

以受油機作定直平飛為基準狀態,飛行速度為100 m/s,飛行高度為5 000 m,進行配平并線化,加油錐套相對受油機的初始位置為(100,50,-50)。配平并線化后,式(15)中受油機狀態矩陣、控制矩陣、輸出矩陣分別為

--------------------

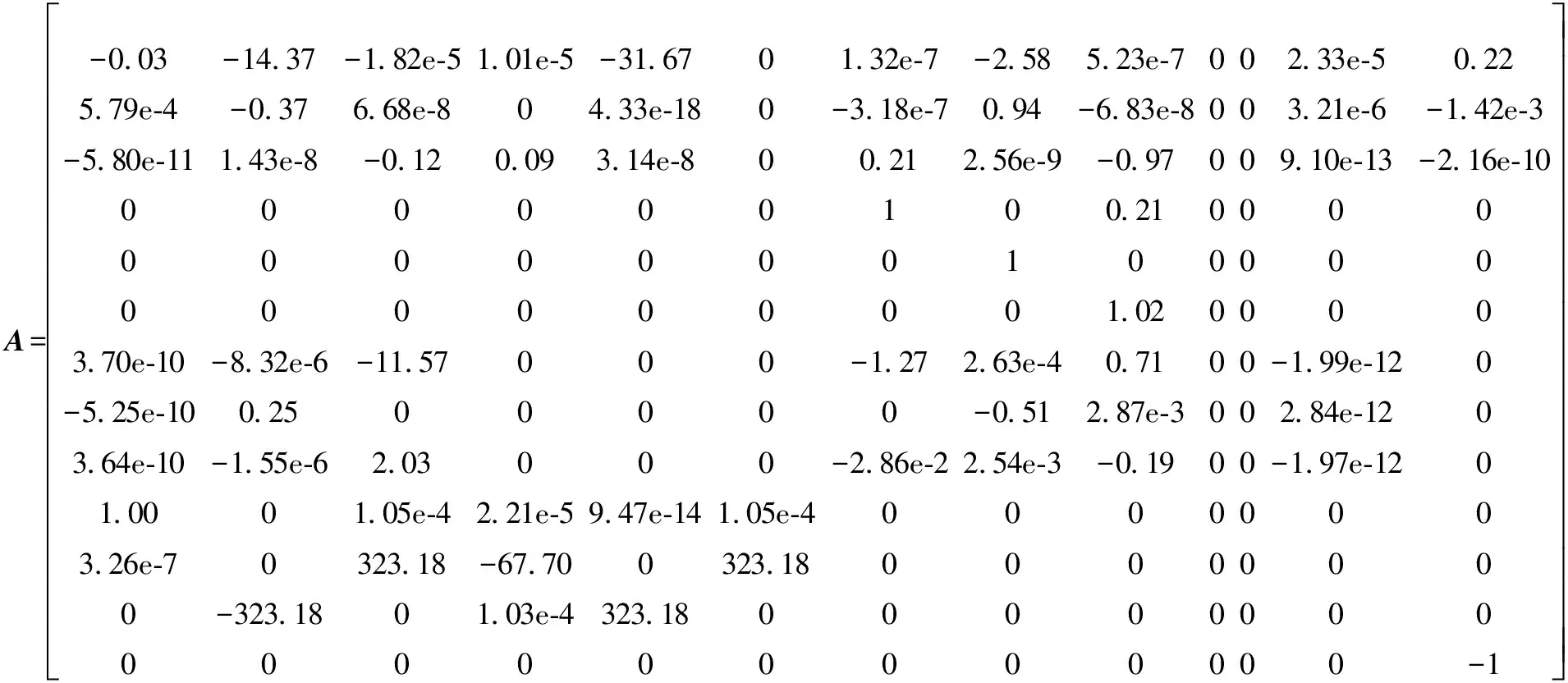
基準控制器的設計參數取為

Q=diag(20,10,10,1,10,10,1,1,1,
20,10,20,10,10,220,200,200)

R=diag(80,800,900,2 300)

其中,diag(·)表示以括號內元素為對角元素的對角陣,矩陣中除對角元素外全為0。

自適應控制器設計參數取為

ΓΘ=(0.1,0.1,1,1,1,1,1,1,1)×500
ΓU=(1,100,100,100)

仿真過程中,對受油機系統矩陣中各元素進行±30%的隨機攝動,以模擬建模誤差及參數不確定性。同時,在80 s時加入持續時間為10 s的Dryden紊流,在100 s、110 s、120 s依次加入x、y、z方向的突風,以檢驗控制器的抗風擾動性能。風擾動情況如圖20所示。

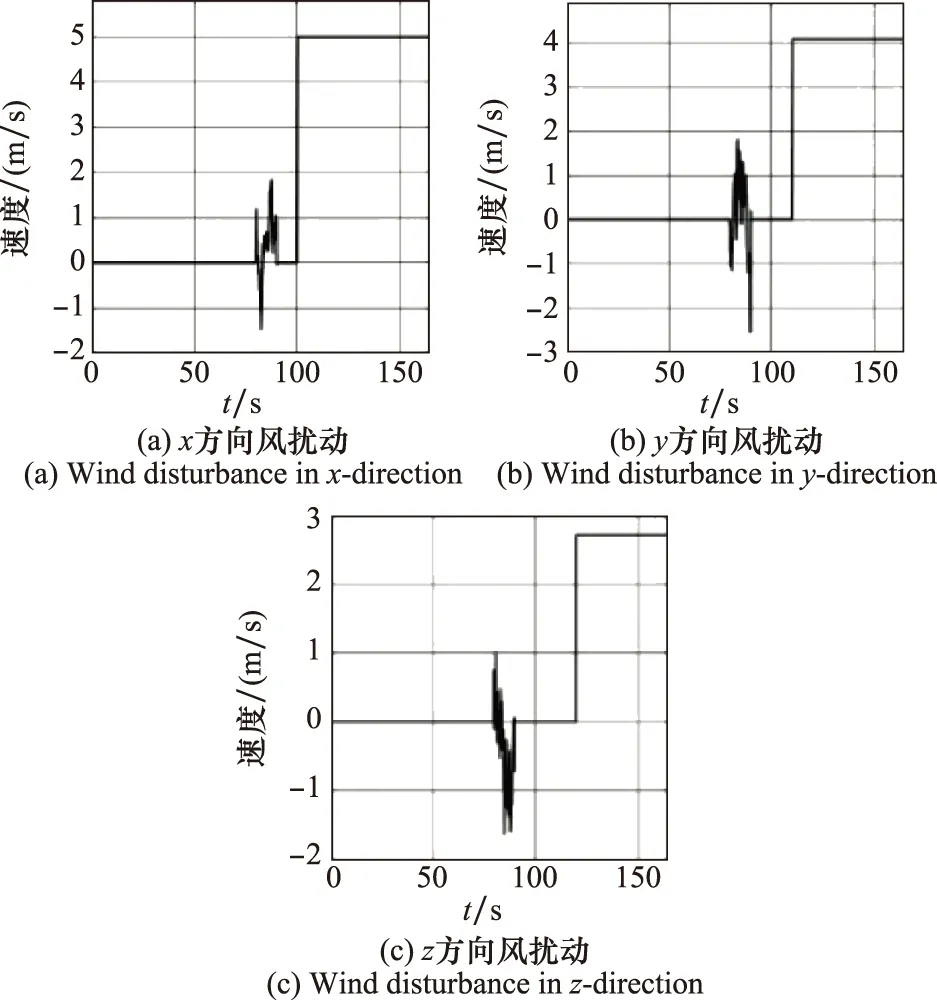
圖20 風擾動Fig.20 Wind disturbances

指令跟蹤的仿真結果如圖21所示,結果表示為相對受油機于起始位置定直平飛時狀態的增量。在無風擾動的情況下(80 s前),基于RSLQR增廣的兩種MRAC控制器均能使受油機跟蹤參考軌跡,模型參數的攝動使自適應控制器的跟蹤精度優于文獻[29]提出的NZSP控制器。加入風擾動后(80 s后),NZSP方法可使受油機穩定,但受擾動后震蕩幅度顯著大于受投影MRAC控制的受油機;而使用傳統的MRAC方法(不引入投影算子)時,在持續風擾動作用下受油機出現大幅度震蕩,其原因在于式(35)中自適應量沒有引入約束機制,當實際狀態與參考模型狀態差異較大時易引起控制量發散。

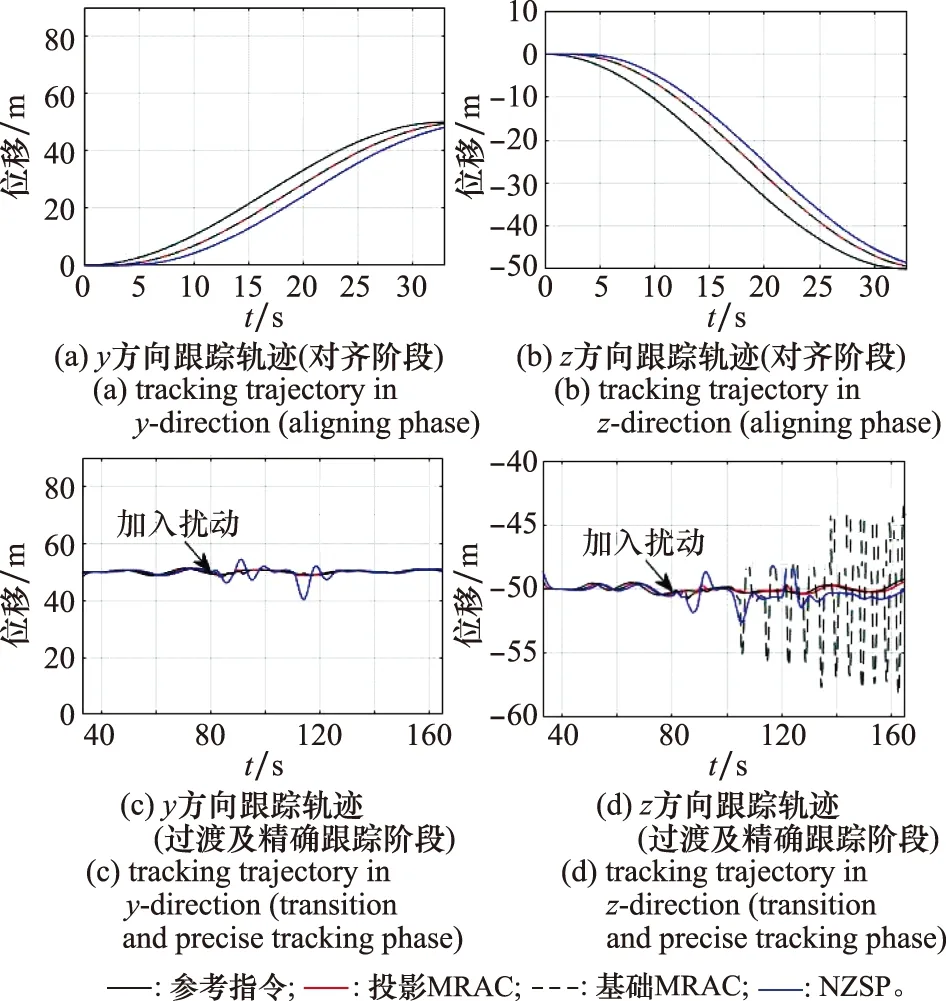
圖21 y、z方向的指令跟蹤Fig.21 Command tracking in y, z direction

圖22顯示,當存在風擾動時,各控制面的偏轉角度及角速率在各自限值內(所選受油機模型舵面偏轉角限值為±25°、±21.5°、±30°,偏轉速率限值為±60°/s、±60°/s、±120°/s)。氣流擾動帶來較大的瞬時偏轉速率,可通過距陣R進行調節。

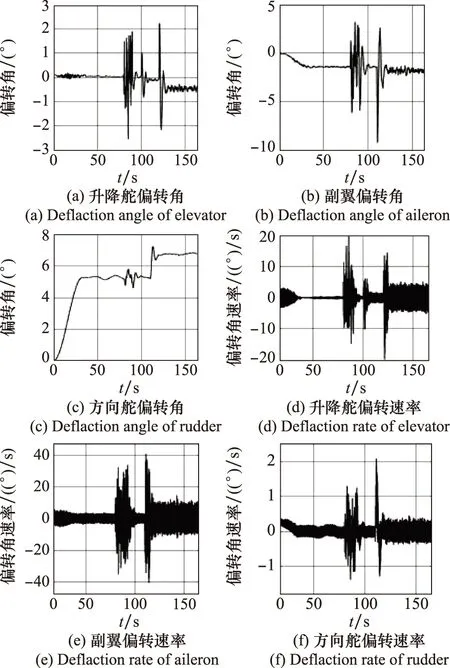
圖22 控制面偏轉情況Fig.22 Deflection of control surfaces

完成對齊階段后,受油機在y-z平面內的跟蹤誤差如圖24所示。以加油錐套的捕捉半徑0.4 m為閾值,統計無風擾動的情況下精確跟蹤階段內跟蹤誤差小于閾值的概率為80.73%,即受油機在該階段有80.73%的可能性對接成功,如圖24(a)。存在風擾動時,如圖24(b),受油機在紊流作用下跟蹤誤差出現一定程度的增大,在紊流停止后經過5 s左右回到較低誤差水平;在突風起始時刻受油機出現較大跟蹤誤差,經過5 s左右回到較低誤差水平,在風場穩定后跟蹤誤差與無風擾動時基本一致。

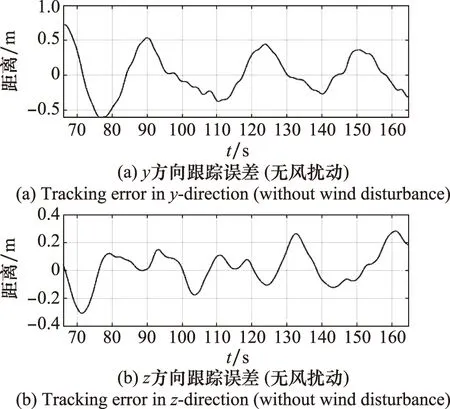
圖23 y-z平面內的跟蹤誤差(無風擾動)Fig.23 Tracking error in y-z plane (without turbulence)

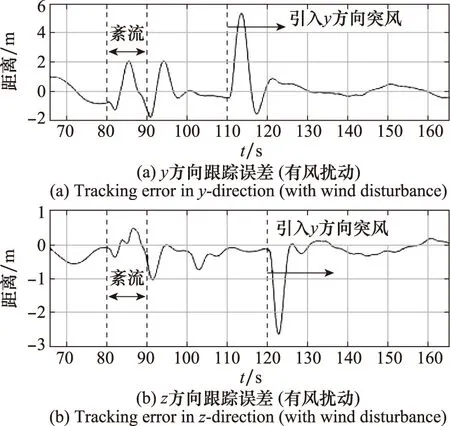
圖24 y-z平面內的跟蹤誤差(有風擾動)Fig.24 Tracking error in y-z plane (with turbulence)

經反復試驗,控制器設計參數影響如下:

(1) 增大Q陣對角線上的最后3個元素有助于抑制指令跟蹤誤差的產生,但同時將增大舵面偏轉;增大R陣對角線上的元素有助于抑制舵面偏轉,但同時將增加跟蹤誤差,在構造基準控制器時需權衡調整達到理想狀態;

(2)增大自適應控制器設計參數ΓΘ、ΓU有助于減小圖25所示的參考模型跟蹤誤差,即存在模型參數不確定性的飛機能更好地跟蹤參考模型的狀態。但該參數過大將使控制量出現較大振蕩,應設計調優。

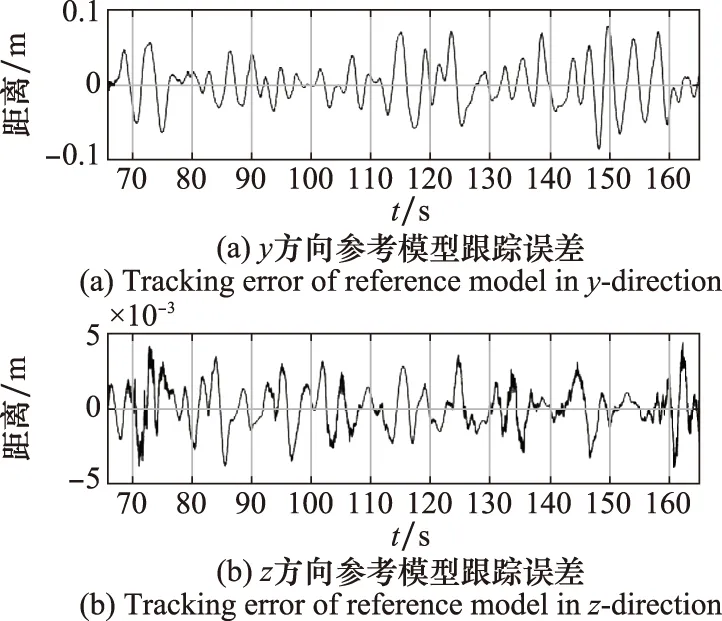
圖25 參考模型跟蹤誤差Fig.25 Error of tracking the reference model

4 結 論

本文針對自主空中加油對接過程中錐套定位問題建立了基于雙目YOLOv4-TSPP的空間定位方案,提出了一種基于YOLO目標檢測結果進行向心八點搜索的錐套橢圓形邊界擬合方法,并利用實體縮比模型進行了目標檢測和雙目測距的試驗驗證;針對空中加油對接控制問題提出了基于投影方法的MRAC增廣控制器,進行了仿真驗證。結果表明:

(1) YOLOv4-TSPP較YOLOv4-Tiny體積更小、性能更好,有較高的目標檢測精度和速度,橢圓邊界擬合方法滿足實時性要求,符合空中加油的實際需求;

(2) 先分別從雙目視野中檢測目標物再進行位置匹配的方式降低了計算量,也從一定程度上擺脫了匹配算法對色彩的依賴度,可以提高雙目測量方法的魯棒性;

(3) 提出的控制方法能有效進行自主對接控制,并在機體參數存在不確定性及存在風擾動的情況下有較強的魯棒性。