具Holling-III型治療函數的SEIR模型及其穩定性分析
郭 宇,朱惠延,賀芳芳
(南華大學 數理學院,湖南 衡陽 421001)
simulation
0 引 言
傳染病一直影響著人類的健康,據世界衛生組織(world health organization,WHO)報告,全球人口數近一半受到了各種不同傳染病的威脅[1]。數學模型對于分析和控制傳染病的傳播發揮著越來越重要的作用,眾多專家、學者通過建立不同的傳染病感染模型來了解以及掌握疾病傳染的機制,從而為控制病情提出合理的解決方案[2]。
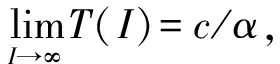
(1)
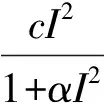
由于模型(1)中前三個方程不含R,因此只需討論前三個方程:
(2)
模型(2)的初始條件為:
S(0)≥0,E(0)≥0,I(0)≥0。
(3)
1 模型的正定性與有界性
由微分方程理論易知,若模型(2)滿足初始條件(3)非負,那么解一定存在,設為(S(t),E(t),I(t))。
定理1 對于任意的t>0,解(S(t),E(t),I(t))非負。
證明:參考文獻[14]的方法,將模型(2)的第一個方程轉化為:
(4)
(5)
對等式(5)兩邊從0到t1積分得:
(6)
同理可得
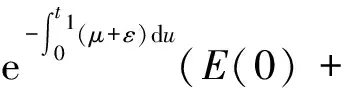
(7)
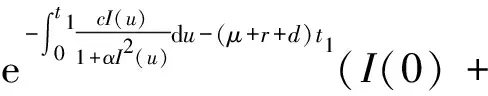
(8)
顯然由式(6)知S(t)>0,現考慮E(t)≥0。假設存在時間t′,使得I(t′)=0,I′(t′)<0,當0
0,I(t)≥0,定理1得證。
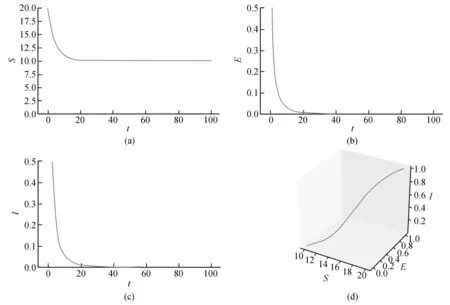
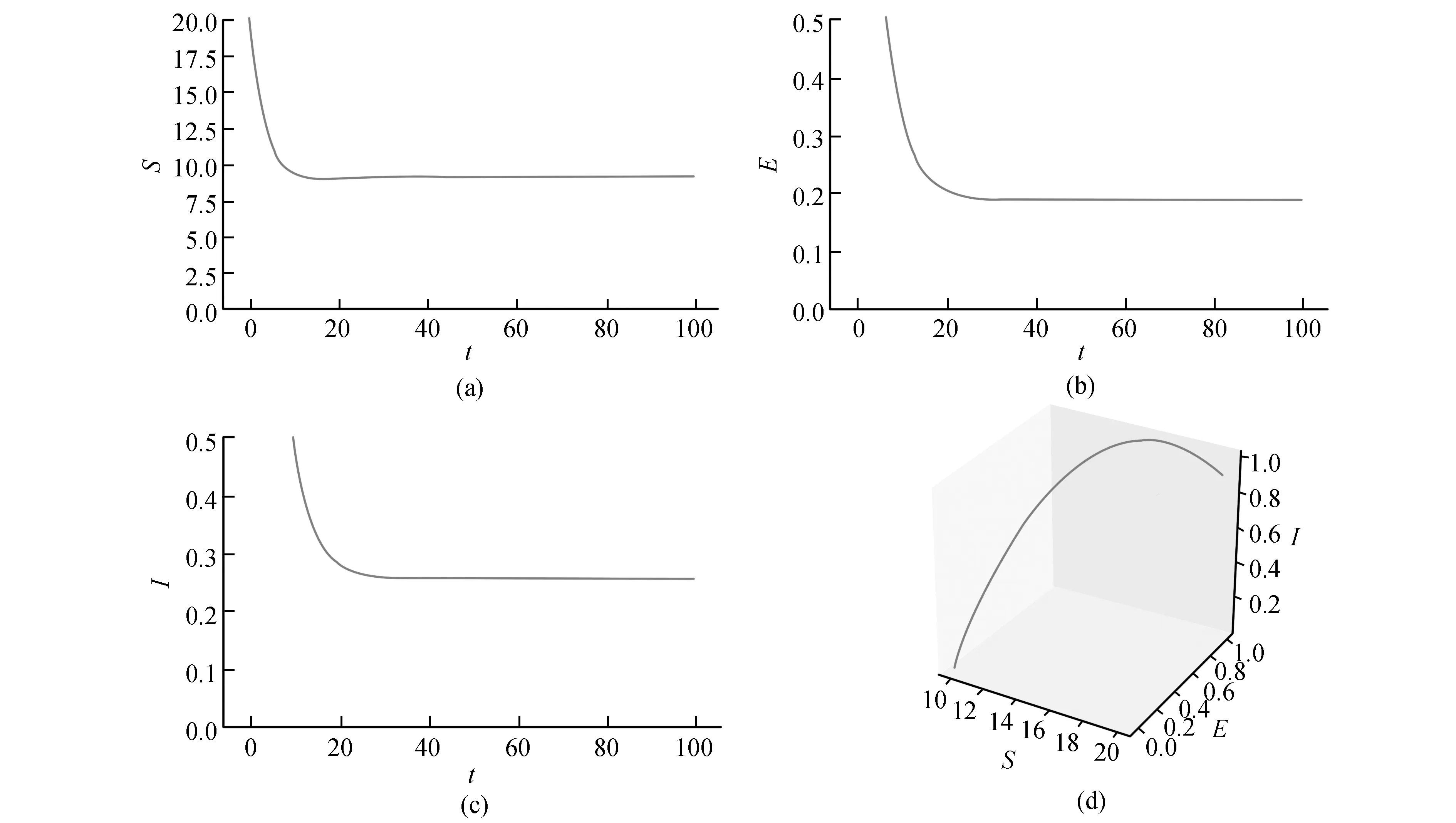
定理2 解(S(t),E(t),I(t))是一致有界的,即存在M>0,使得S(t) 證明:將模型(2)的三個方程相加得: (9) 由式(9)得 (S(0)+E(0)+I(0))e-μt, (10) 設X=(S,E,I)T,將模型(2)表示為如式(11)形式: (11) 其中 求得F(X)與V(X)在無病平衡點處的Jacobian矩陣為: 因此 得到模型(2)的基本再生數為 定理3 當R0<1時,模型(2)中無病平衡點E0是局部漸近穩定的;當R0>1時,E0則不穩定。 證明:模型(2)在E0處的Jacobian矩陣為: 因此特征方程為|λI-J(E0)|=(λ+μ)(λ2+a11λ+a22)=0,其中 a11=2μ+ε+r+d, a22=(1-R0)(μ+ε)(μ+r+d)。 顯然,a11>0,λ=-μ<0為特征方程的一個負特征值;當R0<1時,有a22>0,再結合Routh-Hurwitz判據[16]知|λI-J(E0)|=0的特征根均具有負實部,即當R0<1時,模型(2)中無病平衡點E0是局部漸近穩定的;當R0>1時,E0不穩定。 由模型(2)可求得地方病平衡點為: I*為三次方程b11I*3+b22I*2+b33I*+b44=0的正根,其中 b11=α(μ+ε)(μ+r+d)(β+μb), b22=αμ(μ+ε)(μ+r+d)+c(μ+ε)(β+μb)-Αβεα, b33=(μ+ε)(μ+r+d)(β+μb)+μc(μ+ε), b44=μ(μ+ε)(μ+r+d)(1-R0)。 由于參數都為正數,顯然b11>0,b33>0。若R0<1,可知b44>0;若R0>1,可知b44<0。因此,模型(2)正根個數由b22,b44的符號決定,下面根據笛卡爾符號準則來判斷f(I)=b11I*3+b22I*2+b33I*+b44可能的正根個數。 由表1可以得到如下結論。 表1 方程f(I)=0可能的正根數Table 1 The number of possible positive roots of f(I)=0 定理5 模型(2)的正平衡點有如下幾種情況。 (1)當R0<1,b22>0時,模型(2)不存在地方病平衡點; (2)當R0>1,b22>0時,模型(2)存在唯一的地方病平衡點; (3)當R0<1,b22<0時,模型(2)存在零個或兩個地方病平衡點; (4)當R0>1,b22<0時,模型(2)至少存在一個地方病平衡點。 定理6 當R0>1且0 證明:模型(2)在E1處的Jacobian矩陣為: 因此特征方程為 |λI-J(E1)|=λ3+c11λ2+c22λ+c33=0, 其中 αI*2)2+c+cI*(2b-αI*)), (b(μ+r+d)(1+αI*2)2+c+cI*(2b- αI*))。 由于b(μ+r+d)(1+αI*2)2+c+2cbI*>2b(μ+r+d)αI*2,因此只要滿足2b(μ+r+d)αI*2>cαI*2即c<2b(μ+r+d),M才為正。 顯然,當0 下面通過數值模擬對模型(2)所得的穩定性結果進行驗證。 1)選取參數值Α=2,β=0.05,ε=0.8,μ=0.2,b=5,c=0.5,α=5,r=0.2,d=0.2,由這些參數值可得模型(2)基本再生數R0≈0.667<1,模型(2)存在唯一的無病平衡點E0(10,0,0),且E0是局部漸近穩定的,結果見圖1。 圖1 S,E,I的時序圖與解的軌跡圖(R0<1)Fig.1 Time series of S,E,I of the system and the phase trajectory of the system(R0<1) 2)選取參數值Α=2,β=0.1,ε=0.8,μ=0.2,b=1,c=0.8,α=2,r=0.1,d=0.1,計算得到模型(2)基本再生數R0=2>1,且參數值滿足c<2b(μ+r+d),b22=0.08>0,b44<0,此時模型(2)存在唯一地方病平衡點E1(9.081 9,0.183 6,0.253 4),該地方病平衡點是局部漸近穩定的,結果見圖2。 圖2 S,E,I的時序圖與解的軌跡圖(R0>1)Fig.2 Time series of S,E,I of the system and the phase trajectory of the system(R0>1) 本文建立并研究了一類具Holling-III型治療函數的SEIR傳染病模型,運用常微分方程穩定性理論對模型進行了穩定性分析。研究發現,在基本再生數R0<1處模型只存在唯一的無病平衡點,且無病平衡點是局部漸近穩定的;當基本再生數R0>1時,此時模型不僅存在無病平衡點,還存在一個或三個地方病平衡點。當出現一個地方病平衡點時,本文給出了該地方病平衡點局部漸近穩定所需的條件。對于出現三個地方病平衡點時的情形,其穩定性分析將是我們未來的研究工作。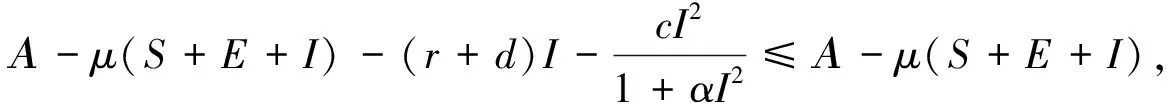
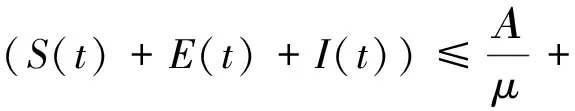
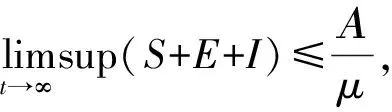
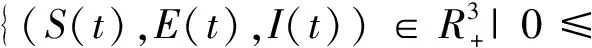
2 無病平衡點與基本再生數
3 地方病平衡點穩定性分析

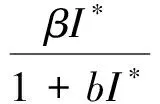
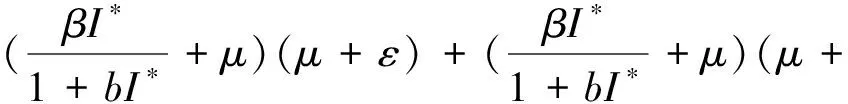
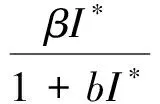
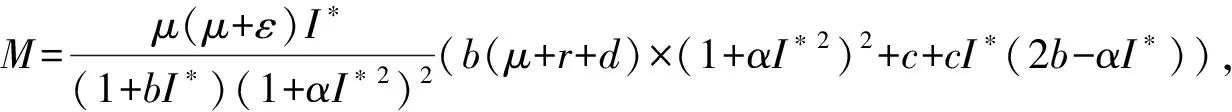
4 數值模擬
5 結 論

