基于坡面卸荷的土質邊坡應力狀態及穩定性分析

楊奎斌，朱彥鵬

(1. 蘭州理工大學土木工程學院，甘肅，蘭州 730050；2. 西部土木工程防災減災教育部工程研究中心，甘肅，蘭州 730050)

邊坡穩定性分析是土力學中的經典問題之一，而坡體應力狀態作為影響邊坡穩定性的一個重要因素，長期以來備受專家學者關注。盧應發等[1]根據坡體變形和力的傳遞特征，認為邊坡滑面在不同位置表現出不同的應力狀態特征；蘇杭等[2]基于邊坡施工后坡體位移的相對變化趨勢，給出了邊坡開挖松弛區和預壓區的明確定義；王浩等[3]解釋了路塹高邊坡開挖卸荷松弛的力學機理，模擬重現了邊坡失穩破壞階段的全過程應力調整規律及發展趨勢；冷伍明等[4]、艾希等[5]為有效改善路堤填土應力狀態，提出了一種新型預應力路基結構，并分析了坡面法向、水平向附加應力擴散規律；李麗華等[6]對廢舊輪胎加筋路堤邊坡進行模型試驗，認為輪胎加筋可顯著改變坡體應力狀態，有利于增強邊坡穩定性；陳金鋒和宋二祥[7]在山區機場高填方邊坡建設中提出了單級反壓護道的優化設計方法，其理念實質也是通過反壓改變坡體受力狀態，進而提高邊坡穩定性。由此可見，無論是邊坡開挖卸荷還是支護加載，均與坡體應力重分布密切相關，基于應力狀態對邊坡穩定性進行研究很有實際意義。

在現有邊坡穩定分析方法中，利用條分法建立的極限平衡理論最早產生，根據條間力假設的不同，相繼又有多種不同方法被提出，這些方法概念清晰、計算簡便，在工程中被廣泛應用，然而剛性土條假設無法反映坡體應力場分布情況，且條間力假設所產生的分析誤差始終難以避免。為解決這一問題，部分學者在不引入條間力的情況下，取整個滑體為研究對象，并基于滑面應力假設和修正建立平衡方程進行安全系數求解[8-12]。與此同時，一些學者還借助數值軟件獲取坡體真實應力場，進而根據滑面應力進行邊坡穩定性分析。其中邵龍潭等[13]基于有限元滑面應力分析法對重力式擋土墻進行研究，搜索確定了最危險滑動面和對應的安全系數；吳順川等[14]根據滑面應力狀態提出了邊坡安全系數新解法，能夠有效解決非等比強度折減方案中邊坡穩定性評價指標的確定；張海濤等[15]給出了矢量和的滑面應力抗滑穩定分析新思路以及矢量和形式的安全系數；李忠等[16-17]通過建立邊坡非線性有限元計算模型，提出了基于滑面應力控制的邊坡主動加固計算方法，并將有限元計算與多種群遺傳算法結合，建立了一種基于MPGA 的復雜應力狀態邊坡穩定性分析通用模型；Stianson 等[18]利用有限元所得應力對邊坡穩定性進行研究，總結了土體泊松比和彈性模量對穩定性安全系數的影響規律；Liu 等[19]將有限元應力場用于多種不同類型邊坡，進一步拓寬其在邊坡穩定性分析中的適用性。顯然，以上這些方法為邊坡穩定性研究提供了很好的思路，但利用條分法建立的極限平衡理論始終難以考慮土體應力狀態，坡體滑面應力計算又長期停留在數值方法上。

為了有效獲取坡體應力狀態，本文基于坡面卸荷應力等效思路，將邊坡視為水平地面經開挖后形成的坡體，并利用彈性理論對坡內土體任一點進行應力求解，進而根據滑面應力計算邊坡穩定性安全系數，最后結合多個算例對潛在滑動面位置及穩定性安全系數進行比較來驗證其合理性。

1 坡面卸荷應力等效分析思路

具有一定高度和坡度，存在臨空面的坡體，可以將其認為是自然水平地面經開挖后形成的斜坡。當開挖部分挖除卸荷后，原本作用在坡面上的應力將得到釋放，所以坡體內任一點應力由兩部分組成：一部分是開挖前自然水平地面所對應的豎向自重應力和水平自重應力；另一部分則是卸荷引起的應力改變量。

需要說明的是，坡面卸荷是一個應力釋放、應力重分布過程，在坡面處的卸荷等效應該采用應力等效，而非荷載等效，如圖1 所示。后者被蘇聯專家弗洛林 B·A[20]在《土力學原理(第一卷)》中提到，筆者認為兩者在本質上存在不同，應力等效較荷載等效更為合理。

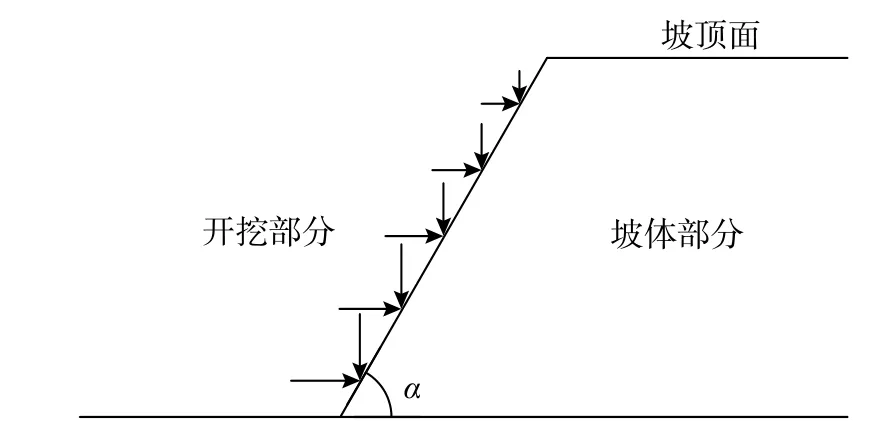
圖1 坡面卸荷應力等效示意圖Fig. 1 Stress equivalent diagram of slope unloading

坡面上任一點豎向和水平向卸荷應力可根據土力學按深度求得，其中均質土按下式計算，成層土則進一步考慮每層土性質。

式中： γ為土體重度；y為坡頂面以下深度；K0為土的側壓力系數，理論上有K0=ν/(1-ν)，ν為土的泊松比。

為方便計算，取坡面土單元進行受力分析時，可將卸荷等效應力轉換為作用于坡面的法向應力 σα和切向應力τα，其沿坡面分布如圖2 所示。

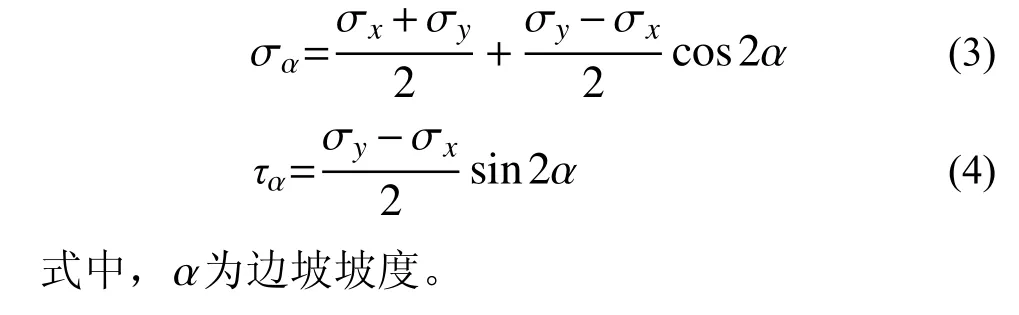
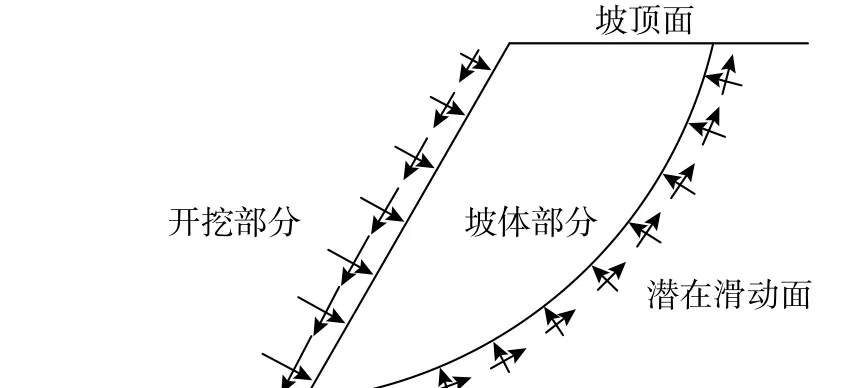
圖2 坡面等效應力分布Fig. 2 Equivalent stress distribution of slope surface

顯然，只要計算出圖2 中坡面卸荷應力對坡體內應力的改變量，即可獲得重分布后的坡體應力場，進而以此得到潛在滑動面上的應力狀態。

2 坡體內一點應力計算

對于二維邊坡而言，可以將其視為平面應變問題，這樣在進行坡面卸荷應力釋放量計算時，能夠將坡面按彈性半無限邊界考慮，并采用彈性理論進行附加應力積分處理，具體計算過程如下。

2.1 計算模型與參數

根據式(1)～式(4)可將坡面線上任一點切向力和法向力簡化如下：

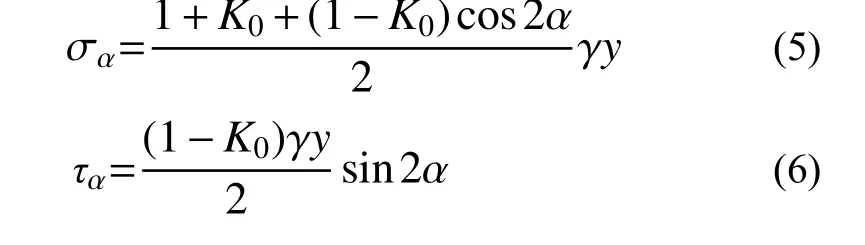
2.2 坡面法向卸荷應力作用下的附加應力

本文以壓應力為正，剪應力則以使單元體逆時針旋轉為正，反之為負，半無限體在邊界上受法向集中力時如圖3 所示。

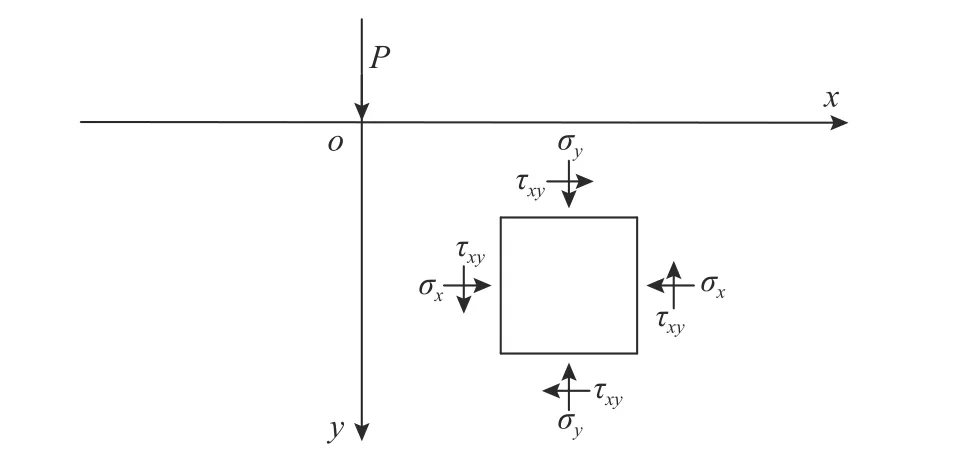
圖3 半無限體邊界受法向集中力Fig. 3 Normal force on boundary of semi-infinite body

圖3 中任一點附加應力計算公式可根據彈性半無限體在邊界上受法向集中力作用的Boussinesq解[21]在無限長范圍內積分得到的Flamant 解[22]確定，也可利用楔形體楔頂受集中荷載作用的彈性應力解[23]確定：

在x′oy′坐標系下對式(7)～式(9)進行坡面范圍內積分，可得坡面法向卸荷應力作用下坡體內附加應力值，具體求解根據積分式采用MATLAB 中的int 函數進行。

式中：b為坐標原點至坡腳的距離； η為坡面任一法向應力作用點至坐標原點的距離；x′、y′為x′oy′坐標系內任一點坐標。

圖4 坡面受法向應力作用分析模型Fig. 4 Analysis model of normal stress on slope surface

2.3 坡面切向卸荷應力作用下的附加應力

同理，半無限體在邊界上受切向集中力時如圖5 所示，任一點的應力計算公式為[23]：

圖5 半無限體邊界受切向集中力Fig. 5 Tangential force on boundary of semi-infinite body

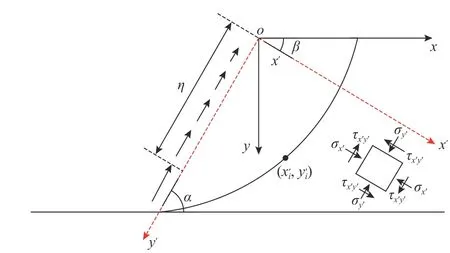
圖6 坡面受切向應力作用分析模型Fig. 6 Analysis model of tangential stress on slope surface

2.4 xoy坐標系內坡體應力轉化

在x′oy′坐標系內，坡體內任一點卸荷應力改變量為坡面法向、切向卸荷應力所引起的附加應力之和。

3 穩定性分析方法

3.1 潛在滑動面形式選擇

通過對圓弧、對數螺旋線等現有潛在滑動面曲線形式，以及相應搜索方法的比較，筆者提出了搜索量小，易于編程，且具有一定物理意義的最速降線形滑動面，由于篇幅有限，在此不再贅述，具體搜索模型如圖7 所示。

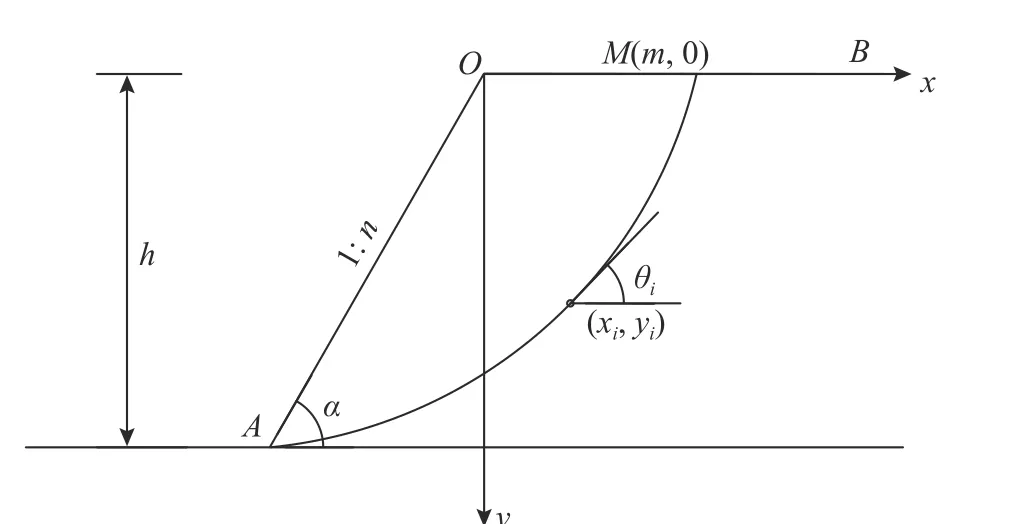
圖7 邊坡潛在滑動面搜索模型簡圖Fig. 7 Sketch of searching model for potential sliding surface of slope

圖7 中線段OA、OB為邊坡表面，曲線AM為最速降線滑動面，以點O為坐標系原點，當M點的坐標為 (m,0) 時，潛在滑動面曲線AM的參數方程如下：

式中：r為最速降線對應的旋轉圓半徑；t為旋轉圓轉動經過的角度。

顯然，要確定最速降線滑動面參數方程需要求得r，以及自變量t的取值范圍，其求解過程如下：

1) 將滑出位置A點坐標 (a,b)代入滑動面參數方程可求得滑出點處自變量的邊界值t′，由此得出自變量t的取值范圍為 (t′,0)。

2) 再將滑出點坐標 (a,b)及滑出點處自變量的邊界值t′代入參數方程，即可求得r值。

搜索過程中，假定滑動面經過坡腳，由此便可通過移動M點位置進行潛在滑動面搜索。

3.2 滑面應力計算

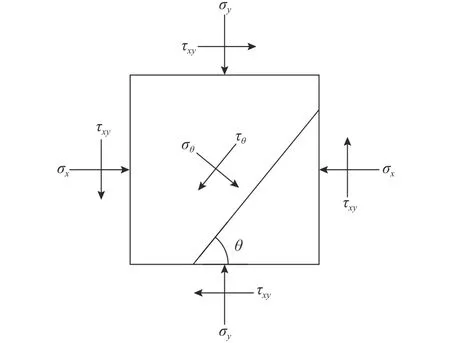
圖8 滑面單元應力分析模型Fig. 8 Analysis model of stress on an element of slip surface

式中， θ為xoy坐標系內滑動面切線與x軸夾角。

3.3 安全系數計算

4 算例分析

4.1 未支護均質土坡

4.1.1 算例概況

為說明坡面卸荷應力等效思路在邊坡穩定性分析中的可行性，選用多個文獻[24 - 26]中均用到的一個經典邊坡算例進行分析比較，邊坡高度20 m，坡度為45°。這里為便于觀察比較，取坡腳處為坐標原點，滑面應力計算仍按2.2 節和2.3 節坐標系進行，具體計算模型如圖9 所示，巖土材料參數如表1 所示。

說到吳琮，夏霖和他雖然是同桌，但平時并沒有太多來往。主要的原因是，夏霖很多次找他說話，他都不予理會，吳琮給人的感覺就是“高冷”。而且在夏霖的印象中，她從沒見過吳琮和誰要好，他總是獨來獨往，像個透明人一樣，常常被大家視而不見。

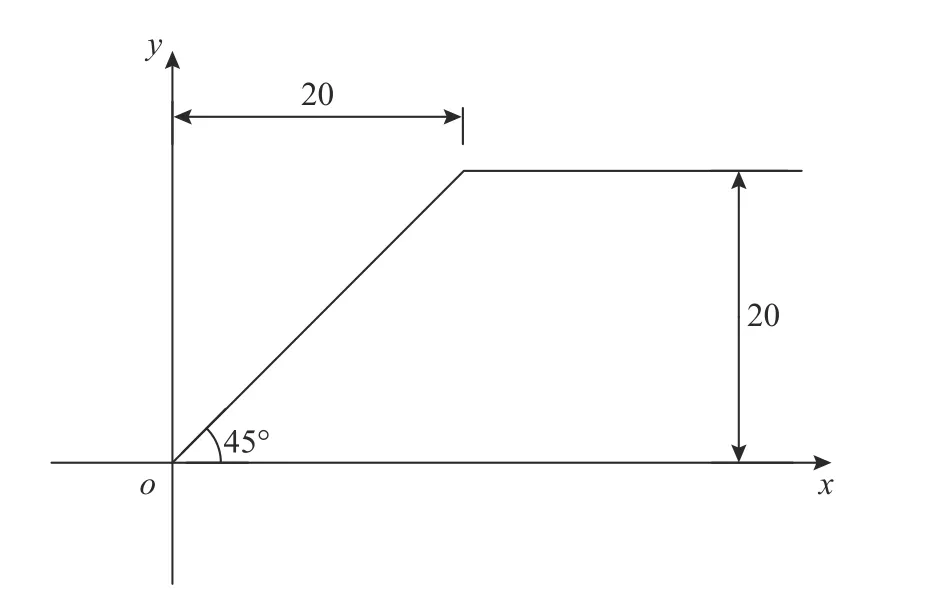
圖9 算例1 的邊坡尺寸 /mFig. 9 Slope size of classical Model 1

表1 算例1 的材料參數Table 1 Material parameters of Model 1

4.1.2 滑動面位置及安全系數比較

借助MATLAB 編制計算程序，實現沿坡頂面移動滑入點位置進行滑動面搜索，最終尋找出最小安全系數對應的潛在滑動面，經搜索得到安全系數隨滑入點位置變化情況，如圖10 所示。

從圖10 中可以看出，當滑入點距坡頂邊緣8 m左右時安全系數最小，通過進一步提高搜索精度，得到邊坡潛在滑動面滑入點位置為(27.7，20)，穩定性安全系數為1.148。與此同時，為驗證計算結果的合理性，將其與已有文獻和極限平衡法相應結果進行比較，其中潛在滑動面位置比較如圖11 所示，穩定性安全系數對比如表2 所示。

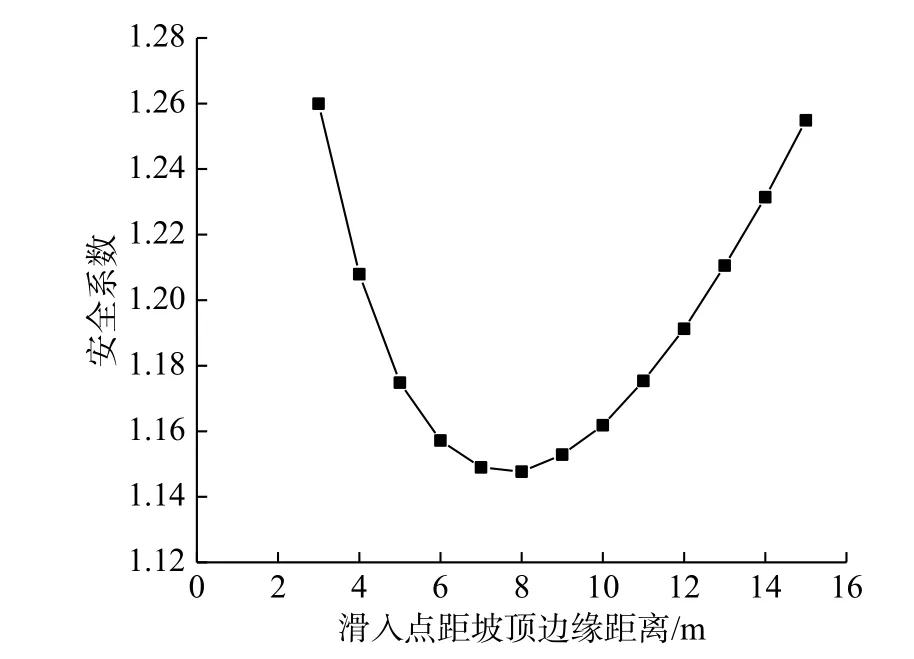
圖10 安全系數與搜索位置關系曲線Fig. 10 Relationship curve between safety factor and search location

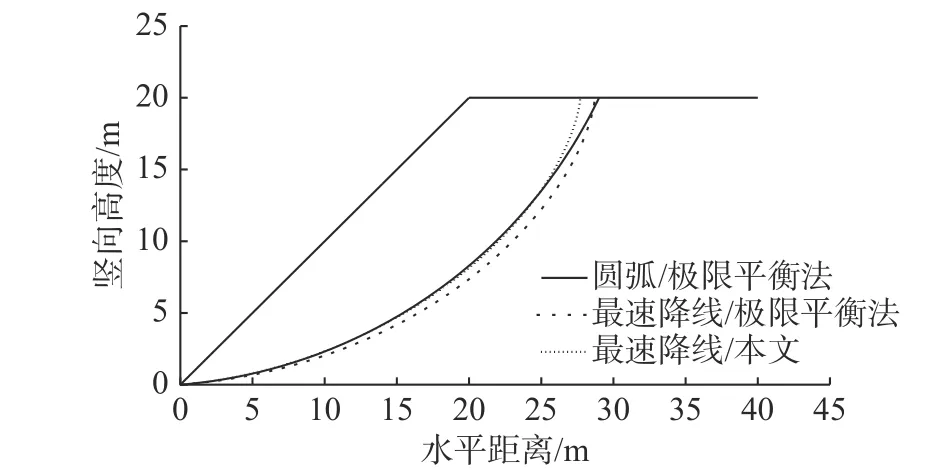
圖11 不同方法潛在滑動面位置比較Fig. 11 Comparison of potential sliding surface positions obtained by different methods

表2 不同計算方法所得安全系數對比Table 2 Comparison of safety factor from different calculating methods

結合圖11 和表2 可以看出，基于坡面卸荷應力等效思路所得結果與傳統方法計算結果基本一致，其中潛在滑動面位置吻合度較好，滑入點較極限平衡法所得位置略有前移。穩定性安全系數方面，較已有文獻以及極限平衡法結果略微偏小，分析認為有以下幾點原因：

1)坡體內應力求解時將坡面按彈性半無限邊界進行假設，所得滑面應力存在一定偏差，會影響到穩定性安全系數值。

2)有限元方法雖然能夠充分考慮土體應力-應變關系，但在邊坡穩定性分析時采用的強度折減法卻存在著一些不足[27]，尤其在折減方法及失穩別標準上，尚未形成統一，受人為因素影響較大。

由上述分析可以看出，經典算例所得結果與強度折減法、極限平衡法吻合度較好，但坡面按彈性半無限邊界假設對計算結果有一定影響。為說明其影響程度，并充分驗證坡面卸荷應力等效思路在邊坡穩定性分析中合理性，有必要在經典算例基礎上繼續對滑面應力進行比較，以及采用更多衍生算例對安全系數影響因素作進一步討論。

4.1.3 滑動面應力比較

選用有限元軟件Plaxis 開展數值模擬，進行坡體內應力值對比，尤其是滑面應力比較，其中土體材料模型采用Mohr-Coulomb，考慮到計算精度要求，模型下邊界為坡腳以下10 m，左邊界為坡腳向左10 m，右邊界為坡頂向右30 m，網格密度為很細，有限元模型如圖12 所示。

圖12 經典算例有限元模型Fig. 12 FE model of classical example

經計算，得到能夠反映潛在滑動面特征的增量位移云圖，如圖13 所示，對應的穩定性安全系數為1.157，這與4.1.2 節分析的滑動面位置和安全系數大小一致，說明基于此模型進行滑面應力比較合理可行。因此，在基于坡面卸荷應力等效思路搜索得到的潛在滑動面上選取3 個參考點，與有限元模型相應位置應力進行比較，其中point1位于滑面下部，point2 位于滑面中部，point3 位于滑面上部，如圖14 所示，所得參考點應力值如表3所示。

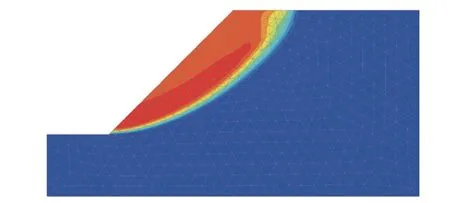
圖13 模型增量位移云圖Fig. 13 Incremental displacement nephogram of model

圖14 滑面應力參考點選取Fig. 14 Selection of reference points of stress on sliding surface

從表3 中可以看出，坡體按彈性半無限體計算得到的豎向應力和滑面中下部剪應力與有限元結果接近，水平向應力與有限元結果存在偏差。分析認為這種偏差由坡面卸荷應力等效和坡面半無限體假設共同造成，主要是因為邊坡臨空面的存在使得水平向應力計算受假定條件影響較大。但總體來看，豎向應力相較于水平向應力、剪應力而言數值明顯偏大，在應力狀態中具有主導作用，經變換后得到的滑面法向應力、切向應力與有限元結果相差不大。

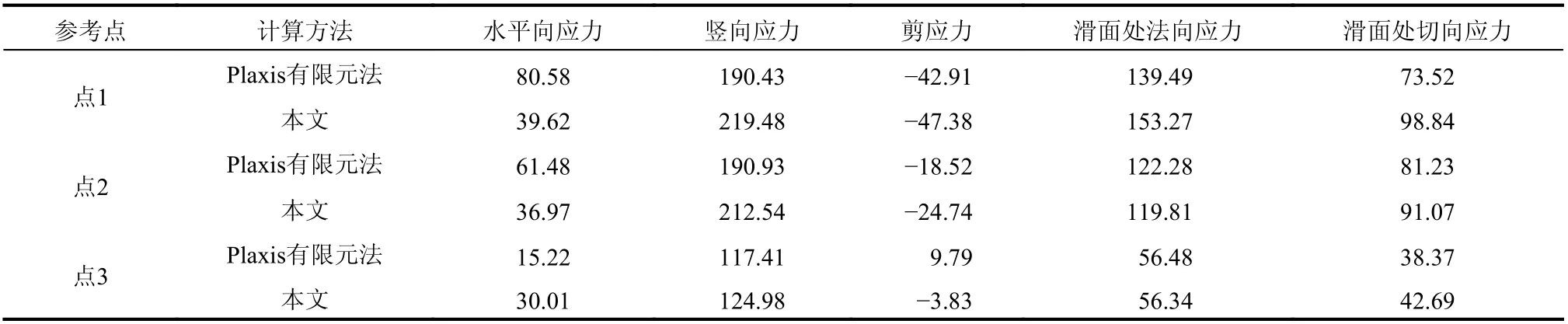
表3 參考點應力對比 /kPaTable 3 Stress comparison at reference points

為全面掌握滑面應力分布情況，沿滑面將計算得到的法向、切向應力與自重應力、有限元相應結果進行比較，其中自重應力由滑面以上土體自重沿滑面法向和切向分解后得到。由此滑面法向應力分布如圖15 所示，滑面切向應力分布如圖16所示。

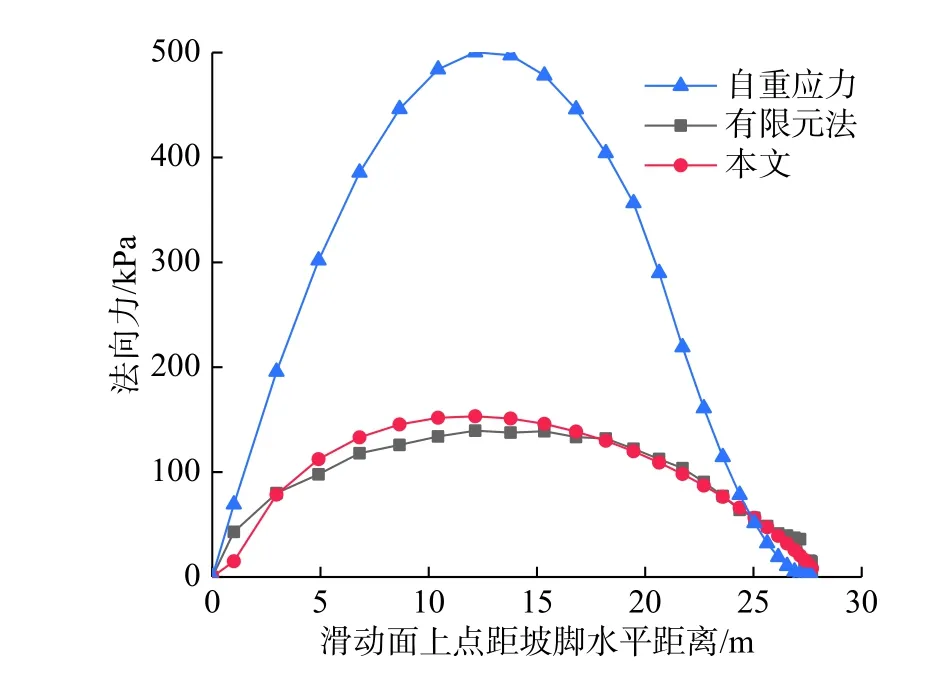
圖15 滑面法向應力比較Fig. 15 Comparison of normal stress on sliding surface

經圖15、圖16 比較可以看出，三種計算方法得到的滑面法向應力與切向應力變化規律相同，均是在滑面中部應力最大，但應力分量數值大小存在一定差異。總體看來，按彈性半無限體求得的滑面應力介于自重應力分量與有限元所得應力之間，與有限元結果接近，與自重應力分量相差甚遠。由此說明，不能將滑面應力簡單的視為自重應力分量，而按彈性半無限體進行滑面應力計算實際可行，這一點也驗證了王鄧峮等[28]、雷軍和肖世國[29]將坡面視為彈性半無限邊界后按彈性理論進行預應力錨桿附加應力分析是正確的。

圖16 滑面切向應力比較Fig. 16 Comparison of tangential stress on sliding surface

4.1.4 坡率對安全系數影響比較

取高度為20 m，坡率依次為1∶0.3、1∶0.4、1∶0.5、1∶0.6、1∶0.7、1∶0.8、1∶0.9、1∶1.0、1∶1.1、1∶1.2、1∶1.3 的邊坡進行比較分析，巖土材料參數仍然采用4.1.1 節中給出的參數。經計算，得到安全系數隨坡率變化的對比關系如圖17所示。

圖17 坡率變化時安全系數比較Fig. 17 Comparison of safety factor with slope rate change

從圖17 中可以看出，當滑面曲線形式同為最速降線時，基于坡面卸荷應力等效思路所得安全系數較極限平衡法偏小，相差在8%以內，有限元強度折減法計算結果則介于兩者之間。當坡度系數小于0.8 時，Plaxis 顯示土體將要坍塌，只能說明安全系數小于1，無法得到具體數值，這一點與本文計算所得安全系數小于1 相一致；當坡度系數大于0.8 時，有限元結果也與本文計算所得安全系數十分接近，相差在3%以內。

4.1.5 坡高對安全系數影響比較

取坡度為45°，坡高依次為5 m、8 m、11 m、14 m、17 m、20 m、23 m、26 m 和29 m 進行比較分析，巖土材料參數仍然采用4.1.1 節中給出的參數。經計算，得到安全系數隨坡高變化的對比關系如圖18 所示。

從圖18 中可以看出，基于坡面卸荷應力等效思路所得安全系數始終與有限元強度折減法計算結果接近，相較于極限平衡法而言偏小，但隨著坡高的增加，計算值越來越接近。

圖18 坡高變化時安全系數比較Fig. 18 Comparison of safety factors with slope height change

4.2 預應力錨桿支護邊坡

選用文獻[28]中用到的一個預應力錨桿支護邊坡進行分析比較，邊坡高度8 m，坡度為90°，土體參數如表4 所示，錨桿布置如圖19 所示，每根錨桿施加相同的預應力。

表4 算例2 的土體參數Table 4 Material parameters of Model 2

圖19 算例2 的邊坡錨桿布置圖 /mFig. 19 Prestressed anchor rod layout of slope in Model 2

該算例中除了要計算坡面卸荷引起的應力改變量，還要考慮預應力錨桿作用，因此將預應力分解為水平方向及豎直方向兩個集中力后，按半無限體進行附加應力計算。

當預應力從10 kN 增加到100 kN，對算例2進行穩定性安全系數計算，并將計算結果與文獻[28]進行比較，如圖20 所示。

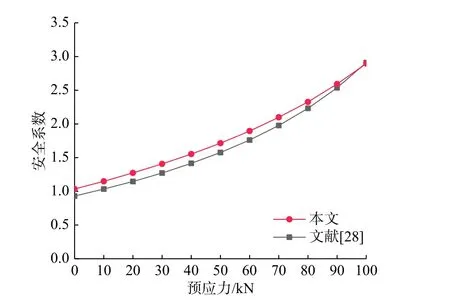
圖20 預應力變化時安全系數比較Fig. 20 Comparison of safety factors with prestress change

從圖20 中可以看出，隨著預應力的增加，安全系數提高明顯，說明錨桿預應力對提高邊坡穩定性十分有效。同時，所得穩定性安全系數整體與已有研究結果十分接近。對比圖17 中采用極限平衡法所得圓弧和最速降線結果可知，安全系數受坡度影響，當坡度較大時，最速降線所得安全系數略小于圓弧相應結果，當坡度較小時，最速降線所得安全系數略大于圓弧相應結果。本算例中安全系數略大于文獻[28]中的相應結果與坡度為90°有關。

5 結論

通過坡面卸荷應力等效思路的提出，將坡面按彈性半無限邊界考慮進行坡體內應力求解和穩定性安全系數計算，并多個算例對其合理性驗證，得出以下幾點結論。

(1)坡面卸荷應力等效思路概念清晰，符合邊坡受力特征，能夠體現臨空面這一決定邊坡穩定性的實質特征，同時，將坡面按彈性半無限邊界考慮可以有效求得坡體內任一點應力釋放值，從而使得邊坡穩定性分析不再局限于條分極限平衡法和數值有限元法。

(2)基于坡面卸荷應力等效思路求得的滑面應力與有限元分計算結果基本一致，搜索得到的潛在滑動面位置，以及對應的穩定性安全系數與有限元強度折減法、極限平衡法計算結果十分接近。

(3)在錨桿支護邊坡穩定性分析中，該計算方法可以有效與支護結構預應力結合，將坡面卸荷與錨桿預應力施加一并考慮，既能反映坡體臨空面的存在，又能體現錨桿預應力的加固作用。

(4)基于坡面卸荷應力等效思路進行的邊坡應力計算及穩定性分析主要適用于土質邊坡，包括均質土邊坡、成層土邊坡和預應力錨桿支護土質邊坡，對于含有順坡結構面的巖、土復合邊坡并不適用。