正交鋼絲環鏈網片頂壓力學行為薄膜等效方法

金云濤，余志祥，駱麗茹，郭立平，張麗君，廖林緒

(1. 西南交通大學土木工程學院，成都 610031；2. 陸地交通地質災害防治技術國家工程實驗室，成都 611756；3. 西南交通大學防護結構研究中心，成都 610031)

柔性防護系統廣泛應用于地災防護工程[1-2]，常用正交鋼絲環鏈網片(以下簡稱環形網)作為攔截部件。網片中網環單元間為接觸式套接邊界，接觸區域外具有只受拉特性，沖擊作用后將發生大變形[3]，其計算方法是當前柔性防護領域的研究熱點。

目前環形網數值模擬常用離散單元法[4-7]和有限單元法[8-10]。早期的數值模型往往將網片內部邊界視作連續處理，如Nicot 等[11]提出了共節點的直桿單元模擬方法，實際上這也是網片模擬的主流近似方法，優點是計算效率高。Yu 等[12]和Hu 等[13]建立了環形網的離散接觸態環梁單元數值模型，提出了等效面積條件下軟化彈性模量的本構關系，該模型大大提高了網片力學行為的模擬精度。羅祥等[14]比較了網片數值模擬中等效面積法和力的平均分配法，并通過理論分析得到圓環等效截面半徑的計算方法。郭立平等[15]揭示了網片面外加載過程中的力流傳遞特征，據此提出了一種基于力流等效的環形網解析計算方法，便于工程簡化設計使用。上述研究推動了柔性網計算理論的發展，但發展更高效率并兼顧精度的環形網數值計算方法依然是當前的關注重點。

雖然環形網的網環單元間具有離散滑移特征，使得單元間的相互運動變得非常復雜，但由于單元幾乎處于僅受拉狀態，這也使得單元受力得以簡化。這使得網片受到面外荷載作用時與薄膜具有很強的相似性，Mentani 等[16]的研究初步利用了這種相似性，使得非線性計算大大簡化，同時獲得了與試驗較為相似的宏觀力學響應，但Mentani 等[16]沒有給出相似等效的解析論證，且其等效網型是菱形網。

為此，開展了3 m×3 m 環形網片的面外加載試驗，研究了試件的P-Δ特性，據此分析并揭示了網片的正交拉力帶傳力特征。基于網片等效力學模型和薄膜最短傳力路徑假定，建立了薄膜面外加載過程的解析模型，研究了等效薄膜的本構關系，推導得到各規格網片的等效應力-應變曲線，并建立了基于等效方法的數值模型，實現了網片在靜載與沖擊荷載作用下的高效計算。

1 網片力學行為

1.1 試驗概述

環形網片面外頂破試驗在西南交通大學防護結構研究中心開展，試件尺寸為3 m×3 m，包括R5/3/300、R7/3/300、R9/3/300、R12/3/300、R16/3/300和R19/3/300 6 種規格，每種規格3 個試件。

試驗設備主要為由鋼結構反力架、液壓千斤頂、位移傳感器、加載單元和頂破頭組成的150 t拉力頂破機(圖1)，頂破頭為加載裝置與網片直接接觸的部分，用于傳遞荷載。

圖1 試驗設備Fig. 1 Test equipment

1.2 試驗結果

網片試件通過卸扣與試驗臺相連，頂破頭在試件布置好之后被推入網片中心區域下方，并與液壓桿連接。加載時，頂破頭提升速度為6 mm/s，通過位移傳感器同步采集提升位移，由后臺數據采集儀記錄生成F-D曲線，直到網片破壞。如圖2所示為不同加載階段環形網片的形態。

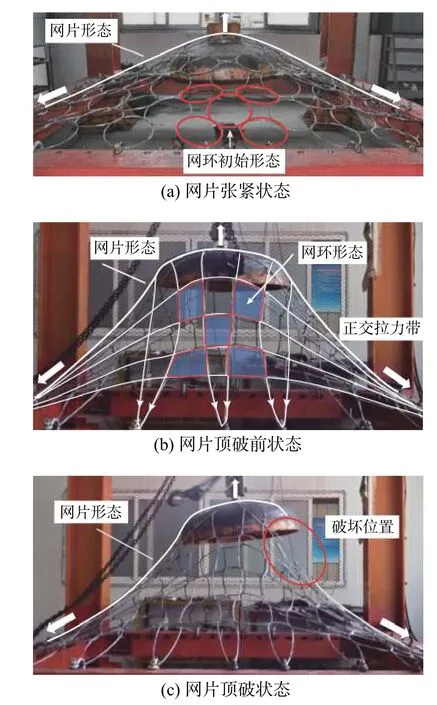
圖2 試驗中的網片形態Fig. 2 Mesh form during test

通過傳感器采集得到的力-位移曲線如圖3(僅列出R5 規格，其余規格曲線特征相似)所示，具體頂破力和頂破位移見表1。

表1 頂破力和頂破位移結果Table 1 Test result of ultimate force and displacement

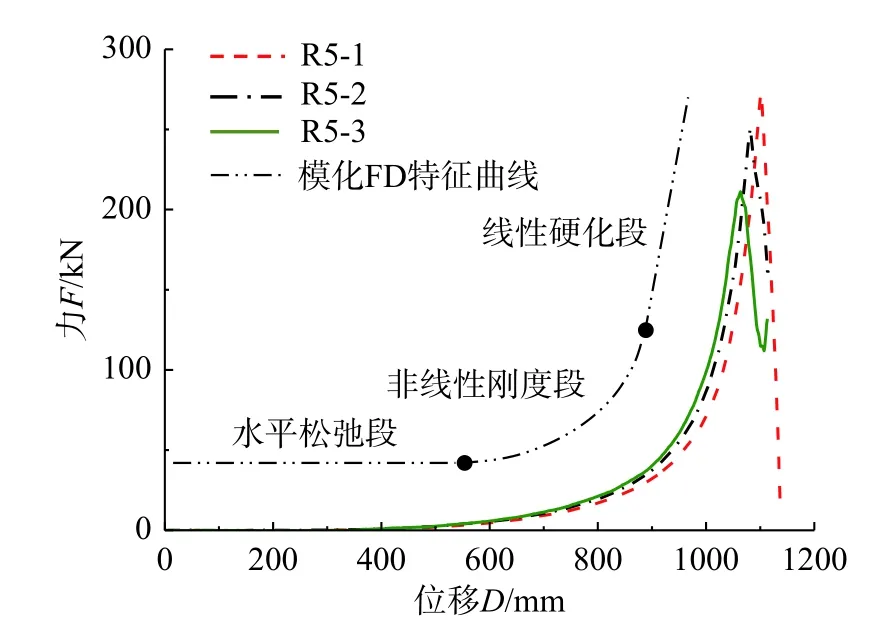
圖3 R5 網片面外加載力-位移曲線Fig. 3 Out of plane loading F-D curves of R5 ring net

分析易知，力位移曲線具有三段特征(圖3)：階段Ⅰ近似為水平直線，因初始松弛影響，網片剛度幾乎為0；階段Ⅱ為曲線，因受網環間嵌套約束影響，網片剛度顯著增加，表現出明顯的非線性受力特征；階段Ⅲ為斜直線，因網環鋼絲束進入軸向拉伸主導階段，網片表現出較大的整體剛度，線性化受力特征較為明顯。最終，因為加載頂頭邊緣對網環的“咬切”破壞，網片到達極限承載力。

1.3 網片-薄膜相似性

環形網受力后呈正交索網狀態，內部網環均具有4 個傳力點(圖4)。網環在受力初都呈環狀(圖2(a))，接近極限狀態時呈矩形(圖2(b))。這是由于隨著荷載增大，網環間滑移會趨于穩定，此后網環單元產生彎直變形，網孔逐漸變為矩形，由于單元拉力沿著軸線方向，因此形成了正交化內力分布模式(圖4)，相鄰平行方向的網環鋼絲束形成了正交拉力帶，其傳力方式類似正交索網。

圖4 網片與薄膜的拉力帶分布Fig. 4 Orthogonal tension band formation

根據試驗結果分析易知，環形網的F-D曲線表現出由強非線性漸變為線性剛化的特征，這在宏觀上與薄膜具有相似性[17]，同時，環形網拉力分布與薄膜在相同邊界條件下的拉力分布亦具有相似性(圖4)，且近似呈正交分布。因此，若能控制薄膜面外加載時具有與網片宏觀上一致的F-D關系，即控制薄膜與環形網具有相同的張拉剛度(見式(1))便可實現兩者的等效，這將大大簡化離散網環間的接觸非線性關系，提高計算效率。

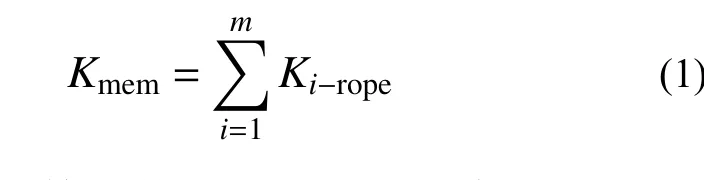
式中：Kmem為等效薄膜面外加載剛度；Ki-rope為網片中各鋼絲束沿加載方向的剛度；m為鋼絲束數量。

2 薄膜等效模型

2.1 解析模型

薄膜等效的關鍵是確定本構關系，為此，基于薄膜正交拉力帶分區假定(圖5(a))，建立解析模型。膜剛度主要來自張拉應力，形成張力剛度，I 區應力普遍較低，甚至存在松弛，因此根據應力分布特征，忽略I 區剛度貢獻。假定加載中任一時刻拉力帶由兩條直線段和一段圓弧組成(圖5(b))，頂頭位移為D，頂頭與薄膜豎向接觸力為F，Ⅱ區長度為l，寬度為b(初始寬度取頂破頭頂壓寬度d=1 m)，鉛垂面內的投影高度為h，厚度為t，與水平面夾角θ。實際頂頭矢高h0=0.109 m，弧長Lr=1.032 m。設局部坐標系y軸沿Ⅱ區拉力方向，x軸為Ⅱ區拉力帶寬度方向，z軸沿薄膜厚度方向(圖5(b))。解析模型滿足幾何條件：

圖5 拉力帶解析模型Fig. 5 Tension band analytical model

設材料原長和終長為L0和L1，各中間歷程的長度分別為L01、L02、···、Ln-1、Ln，對應變增量積分，可得真實應變：

式中：Fy為Ⅱ區拉力帶拉力(圖5)；σy、εex、εez分別為拉力帶y向應力，x向和z向名義應變。式(11)中εex、εez的確定與采用的本構關系類型有關，由式(9)和式(11)，若已知F、D和本構關系類型，可求得相應σy、εty，即可求得薄膜應力-應變曲線，即：

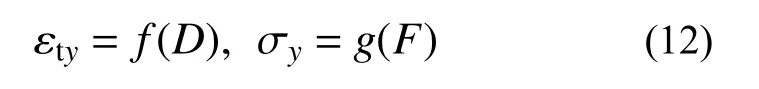
此外，為確定薄膜等效厚度，遵循分布質量一致原則，密度ρ 取環形網鋼絲密度7850 kg/m3。則薄膜厚度t0根據質量一致原則確定：

式中，mn為n圈規格環形網每1 m2質量。每種規格網片相應的等效薄膜厚度如表2。

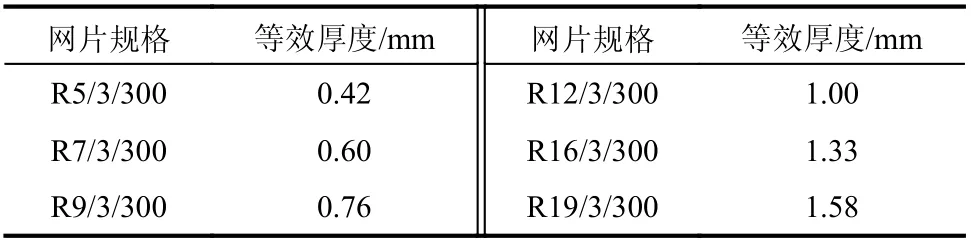
表2 不同規格網片對應的薄膜厚度Table 2 Membrane thickness of different mesh sizes

2.2 薄膜本構關系

由于網環單元間初始具有松弛滑移特征，且這種松弛滑移產生的變形具有不可恢復性，因此構建本構關系時，采用了擬塑性假定，即假定屈服應變為0，加載后材料直接進入屈服平臺，隨后進入強化段。由于塑性變形不引起體積改變[19]，因此引入塑性變形的體積不變條件：

式中：σ、ε 為薄膜的應力及應變；M、N為只與網環圈數n相關的量；e 為自然常數。

計算時，取彈性模量E為各應力-應變曲線失效點處即圖6 中各曲線應變最大的數據點處的切線模量，由于計算得到的各圈數“n”對應薄膜的彈性模量取值差異不大，統一取其平均值11 000 MPa，泊松比取0.3。各圈數“n”對應的薄膜失效應變取圖6 中各失效點橫坐標，并采用線性擬合得到失效應變關于“n”的計算公式：

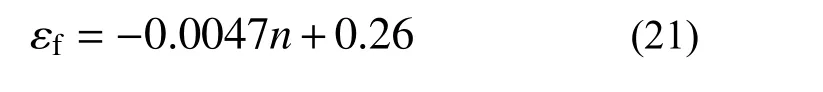
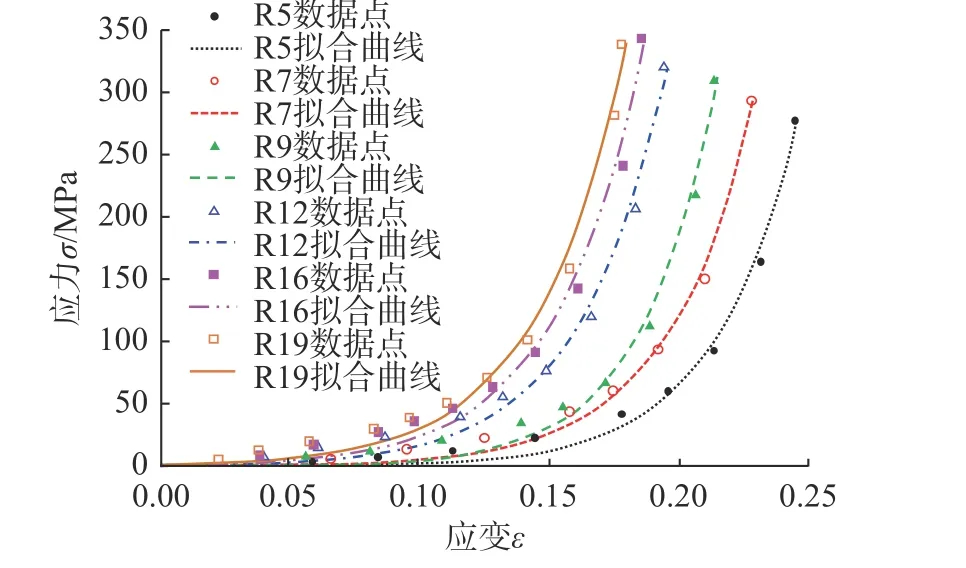
圖6 擬合的薄膜指數強化本構模型Fig. 6 Exponential hardening constitutive model of membrane

2.3 數值模型

薄膜等效的目的是提高網片的非線性計算效率，其求解過程依托數值計算方法，因此需構建相應數值模型。采用顯式瞬態動力非線性分析軟件LS-DYNA 進行計算，采用Belytschko-Lin-Tsay單點積分四邊形殼單元[20-21]，由于單元厚度約為0.42 mm～1.58 mm，與平面尺寸相差3～4 個數量級，其彎曲及剪切剛度的貢獻可忽略不計。薄膜周邊鉸接約束，頂破頭指定向上的強迫位移，薄膜和頂破頭的接觸為采用罰函數和庫倫摩擦模型的面-面接觸，摩擦系數0.4(圖7)。薄膜材料采用2.2 節所述指數強化本構，將薄膜應力-應變曲線(式(18))輸入至數值模型，失效應變取值參考式(21)，薄膜等效厚度取值見表2，網格尺寸25 mm×25 mm。

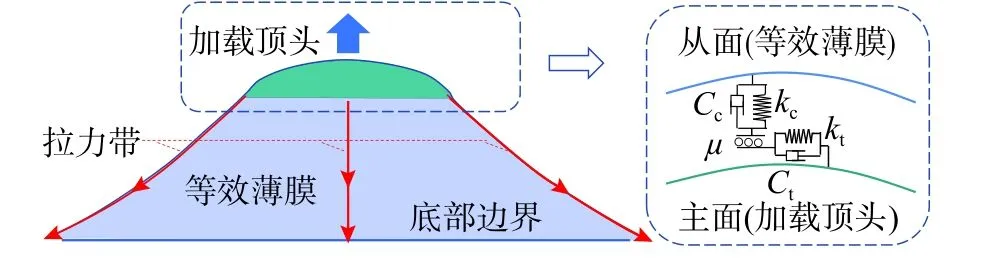
圖7 薄膜面外加載有限元模型Fig. 7 FEM model of membrane out of plane loading

同時采用文獻[13]中的等效面積法建立環梁模型進行對比分析。以R5/3/300 規格的網片為例，將薄膜等效、環梁模型和頂壓試驗結果進行了對比(圖8)，曲線與橫軸包圍的面積即網片的極限耗能。其余規格網片的結果對比見表3。綜合比較來看，環梁模型得到的加載曲線與試驗曲線貼合程度更高，但帶來更高的計算消耗，等效方法的加載曲線同樣能夠還原出初始松弛段、非線性剛度段和線性硬化段的3 階段特征。等效方法的頂破力、頂破位移、極限耗能等指標相對誤差均小于10%，精度與環梁模型相當。值得注意的是，等效方法得到的頂破位移均略小于試驗值，這是因為薄膜等效解析模型忽略了Ⅰ區剛度貢獻，然而數值計算時，Ⅰ區剛度客觀存在，因此導致頂破位移小于試驗值。但兩者差異很小，最大誤差僅為6.6%，這也說明解析模型等效時忽略Ⅰ區剛度貢獻是合理的簡化。

表3 網片面外頂破的等效方法誤差對比Table 3 Relative error contrast between equivalent method and circular beam model

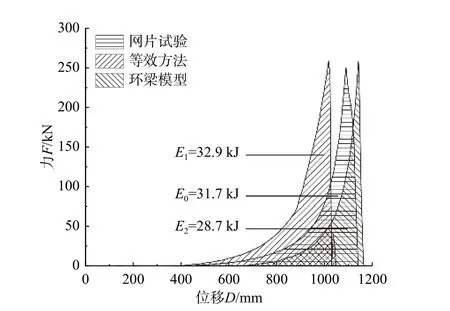
圖8 等效方法力-位移模擬結果對比(R5/3/300)Fig. 8 Simulation results of equivalent method (R5/3/300)

3 等效方法驗證

3.1 網片沖擊試驗驗證

為了進一步研究等效方法用于沖擊荷載作用下的適應性，結合Grassl 等[22]的試驗研究進行了反演分析。Grassl 進行了網片在固定邊界下的沖擊試驗，網片平面尺寸3.9 m×3.9 m，網環規格R7/3/300，四邊固定于剛度很大的支撐鋼框架，沖擊試塊為球體，直徑0.88 m，質量830 kg，沖擊能量45 kJ，試驗通過高速攝像機和固定于試塊上的加速度傳感器得到試塊沖擊過程的位移、速度、加速度時程曲線。

分別建立環形網片沖擊試驗的離散接觸態環梁有限元模型和薄膜等效數值模型。環梁模型的模擬方法為文獻[13]中的等效面積法，采用其所述軟化彈性模量的應力-應變曲線，網環間為通用自接觸，單個網環分為16 段梁單元。薄膜等效模型中薄膜材料參數采用2.2 節所述的指數強化本構模型，應力-應變曲線參考式(18)，失效應變取值參考式(21)，薄膜劃分的網格尺寸25 mm×25 mm，模型的具體輸入參數見表4。薄膜等效模型和環梁模型在各沖擊時刻下的形態如圖9 所示。

圖9 薄膜和網片形態及應力云圖Fig. 9 Form and stress nephogram of membrane and ring net

表4 等效模型輸入參數Table 4 Input parameters in equivalent numerical model

數值模型的計算結果中，t=0.06 s 時，薄膜與網片形態存在微小差異，這是由于環形網的初始松弛影響導致其垂度略大于薄膜初始垂度。t=0.1 s時，網片開始張緊，剛度發展迅速，網片和薄膜變形形態趨于一致。t=0.15 s 時，落錘到達最低點，薄膜和網片的拉力帶效應顯著，具有明顯正交化受力特征，該階段試件剛度發展至極大值。

模擬結果與文獻[22]的試驗結果進行了對比，沖擊試塊位移、速度、加速度時程曲線結果對比如圖10。對比表明，薄膜等效方法得到的加速度峰值與試驗結果相對誤差僅為4.3%，離散網環模型得到加速度峰值與試驗結果相對誤差為3%，兩種數值模擬方法的精度相當。值得注意的是，由位移及速度時程曲線可見采用離散網環模型時，明顯高估了試塊的回彈高度，表明沖擊過程網片的耗能和彈性儲能占比不合理，因此在這點上薄膜等效模擬方法反而具有一定優勢。

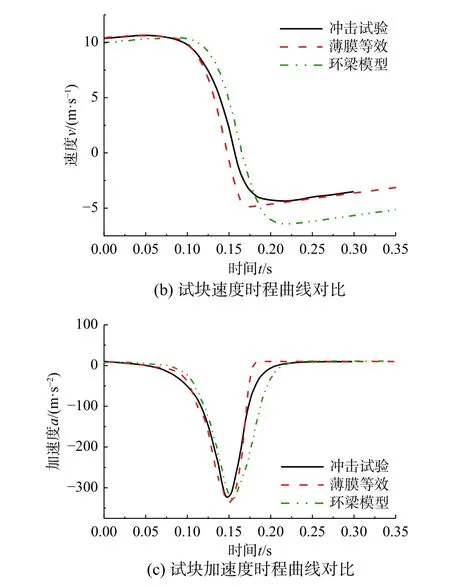
圖10 試塊運動參數對比Fig. 10 Contrast of block motion parameters

3.2 計算效率

對比3.1 節中離散接觸態環梁模型和薄膜等效模型的計算耗時(表5)表明，薄膜等效可以大幅提高環形網的計算效率，測試模型中等效方法計算速度提高10.3 倍。實際上，隨著環形網片計算規模的增加，由于環梁模型內部自接觸導致的計算資源消耗將顯著增加，薄膜等效的優勢將更加顯著。

表5 計算效率對比Table 5 Contrast of computational efficiency

4 結論

綜上所述，可以得到以下結論：

(1)環形網片加載過程中拉力帶效應具有顯著的正交化受力特征，其F-D關系的三階段特征可以通過指數強化本構反演，并結合殼單元薄膜比擬實現力學行為等效。

(2)薄膜等效計算與擬靜力試驗結果的頂破力、頂破位移、耗能誤差均小于10%，等效方法能夠比較準確地反映環形網片面外加載的宏觀力學行為。

(3)薄膜等效方法得到的試塊沖擊變形、速度和加速度時程與試驗結果基本一致，其中加速度峰值誤差為4.3%，精度與離散接觸態環梁模型相當，且等效方法計算效率可提升10 倍以上。

復雜邊界條件下特別是柔性可滑移邊界下的薄膜等效模擬方法需要進一步深入研究。