基于數字圖像投影技術的三維液膜流動測量研究

宋華振，兆環宇，朱程香，王正之，田 偉，李海星，朱春玲,*

1.南京航空航天大學 航空學院，南京 210016；2.上海交通大學 航空航天學院，上海 200240 3.上海飛機設計研究院，上海 201210

0 引言

飛機結冰是飛機飛行中常見的一種現象，對飛行安全危害極大。當飛機穿過含有過冷水滴的云層、結冰溫度較高時，過冷水滴撞擊飛機表面后在氣流的驅動下形成水膜。水膜表面波特性分析可以有效地研究水膜流動和傳熱特性，對探究飛機結冰過程中的質量分布及熱量傳遞意義重大。隨著實驗技術的進步，非侵入性的液膜高度分布測量技術被廣泛應用，其中包括激光誘導熒光技術（Laser Induced Fluorescence，LIF）、反射波技術和圖像處理技術等。

LIF 技術被廣泛應用于定常流可視化測量，其原理是在液體中添加熒光劑，根據熒光劑所激發的熒光強度來判斷流體的速度、高度和溫度。Li 等[1]開發了一種分子標記技術，可以同時測量飛濺水滴的尺寸、速度和瞬態溫度等參數。Johnson 等[2]開發了一種熒光成像系統，量化了等溫條件下薄膜在平坦表面上的瞬態行為。常士楠等[3]利用激光誘導熒光技術測量了一定條件下水膜流動的高度和表面波動特性。

反射波技術中較有代表性的是基于色散共焦位移計的測量方法。該方法通過色散鏡頭將光源射出的寬光譜復色光進行光譜色散，形成不同波長的單色光，每一個波長都對應一個光源到被測物體之間的距離，通過計算被感測到的波長換算距離。Rishikesan 等[4]利用色散共焦傳感器評估不同加工表面的輪廓參數，以此來測量微觀水平表面的光潔度。冷夢堯等[5-6]利用色散共焦位移計對高速氣流驅動下的平板水膜流動進行測量，得到了高速氣流剪切作用下的氣液波動界面剪切因子。

基于圖像處理的結構化光技術也是實現非侵入式高度測量的一種方式，近年來也受到流體動力學界的關注。該技術將已知的光圖案主動投影到物體上，并從一個或多個視點捕獲的光圖案中提取三維表面形狀[7]。Cazabat 等[8]通過投射等距條紋來重構擴散薄膜的剖面高度，研究不同溫度下的薄膜爬升特性。Cobelli 等[9]使用數字條紋投影系統進行實驗，以測量水流的表面變形。Hu 等[10]開發出數字條紋投影系統，并使用該系統定量測量風驅動下的水膜和溪流在平板上的瞬態行為。

在上述測量技術中，LIF 技術憑借著其非侵入式測量和低信號?噪聲比特性得到了廣泛應用。但LIF技術的熒光強度通常依賴于溫度，在不可控變溫過程（如結冰）中很難使用LIF 技術對流體薄膜高度進行定量測量。反射波技術雖然可以對幾乎任何材料進行高精度無侵入式測量[11]，但是無法實時測量三維流體流動的全貌。基于圖像處理的結構化光技術雖能實現非侵入式流體全貌的復現，但也存在圖像處理過程相位變化復雜、流體三維全貌預測精度較低等問題[12]。

數字圖像投影技術（Digital Image Projection,DIP）具有時間分辨功能，是一種全區域水膜高度的測量方法。相比于其他基于圖像處理的結構光技術，DIP 技術可以通過更簡單的圖像處理方法在采集的圖像中提取被測物體的三維表面全貌，且測量精度較好。Zhang 等[13]應用該技術測量NACA0012 翼型表面水膜和溪流隨風速變化的流動過程，復原了水膜在不同風速下的三維全貌，但未建立水膜流動與外界條件間的關系式。國內在DIP 技術方面的相關研究較為少見。

為驗證DIP 技術在流體測量中的可靠性與準確性，本文自主設計搭建了DIP 測量系統和平板水膜流動實驗臺，進行了一系列水膜流動實驗，并利用標準件對DIP 系統測量精度進行了測試。

1 DIP 測量技術

1.1 DIP 測量技術的原理

DIP 測量技術的基本原理如圖1所示。攝像機、投影儀和實驗基板形成三角形布局。在目標流體未流過實驗基板之前，投影儀投射網格圖像于實驗基板，此時攝像機采集實驗基板上的網格圖片作為參考圖像。當目標流體流過實驗基板時，網格圖片將投射于流體表面并發生變形，攝像機記錄此時的變形網格作為測試圖像。通過分析測試圖像和參考圖像對應點的位移，就可以重構被測物體的三維形狀。

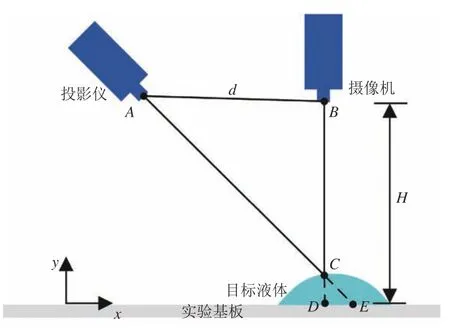
圖1 DIP 技術原理圖Fig.1 DIP technology diagram

為了將測試圖像和參考圖像對應點的位移轉換為目標流體高度分布，DIP 系統需要標定，以建立高度與位移之間的關系。

建立如圖1所示的坐標系，y方向高度為0 的平面為后續測量的參考平面。實驗基板上無任何目標流體時，任意網格點投影于點E；當流體流經實驗基板時，原投影于點E的網格點將投影于關注點C。若此時攝像機的采集方向垂直于實驗基板，根據相似三角形原理可得：

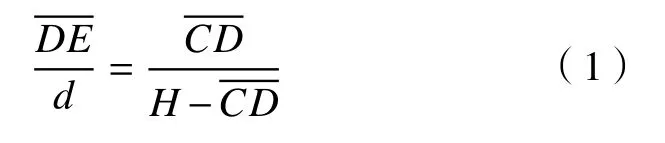
則此時關注點C處的流體高度為：

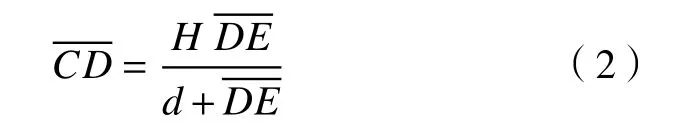
距離d通常遠大于上式可簡化為：

對于給定的DIP 系統，H為攝像機到實驗基板的高度，H和d是固定的，因此參數K 為常數，可由標定方法確定；可通過測量測試圖像和參考圖像之間關注點C處的位移來確定；通過式（3）就可以得出流體流經實驗基板時關注點C處的高度信息，從而復原流體的整個三維全貌。

1.2 DIP 測量的圖像互相關算法

DIP 測量系統使用圖像互相關算法[14-16]來確定測試圖像與參考圖像之間的關注點C處的位移量。在參考圖像和測試圖像的特定區域分別選擇一個小窗口作為關聯窗口，計算兩關聯窗口的相關系數。相關系數R以下式表示：

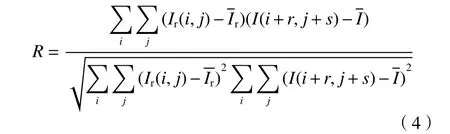
其中，Ir和I分別表示從參考圖像和測試圖像中獲得的關聯窗口的圖像強度，和為相應的平均強度值；i和j分別表示水平方向和垂直方向，（r，s）為圖像位移量。通過找到相關系數的峰值位置就可確定兩關聯窗口的位移量，即關注點的位移量。圖2 展示了一個規則網格的參考圖像和由測試板上的長方塊產生的關注點移動的測試圖像，使用上述算法即可得到紅框內的網格點的位移量。

圖2 網格點位移圖Fig.2 Grid intersection displacement diagram

1.3 DIP 系統的標定方法

對于一個給定的DIP 系統，測試圖像和參考圖像中對應點的位移隨著目標物體的高度變化而呈線性變化。DIP 標定可用于確定測試圖像關注點的位移量與實際高度的轉換系數K。如圖3所示，通過數字投影儀將網格圖像投影到實驗基板上。實驗基板水平安裝于升降臺頂部，升降臺高度（即實驗基板在y方向上的位置）用微米級驅動器調整。攝像機用于捕獲投影在實驗基板上的圖像，所獲取的圖像被存儲在計算機上用于圖像處理。

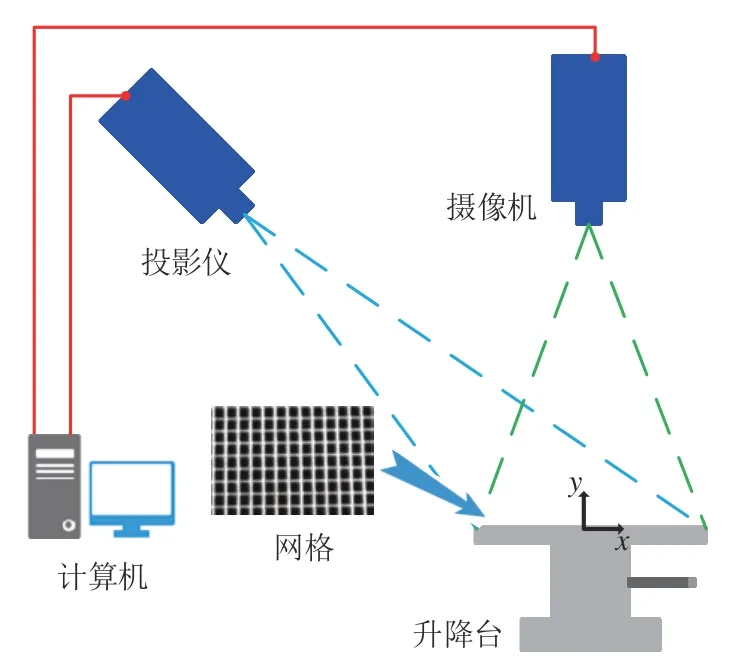
圖3 DIP 標定示意圖Fig.3 DIP calibration diagram

在DIP 標定過程中，通過調整升降臺的高度，將測試板以某一間隔移動到y方向上的多個位置，獲取測試板上投影的網格圖像，再利用圖像互相關算法對圖像進行處理。以y=0 處的圖像作為參考圖像，計算測試板在其他位置時的關注點位移量，從而得到圖像網格點的位移值。圖4 為測試板在不同高度時的測試圖像網格點的像素位移量。從圖中可以看出，高度與網格圖像點的位移量之間的關系可以用線性函數擬合，符合式（3）的線性關系。標定過程得出的線性比例因子即為DIP 測量系統的K值，且K值是一個常數。

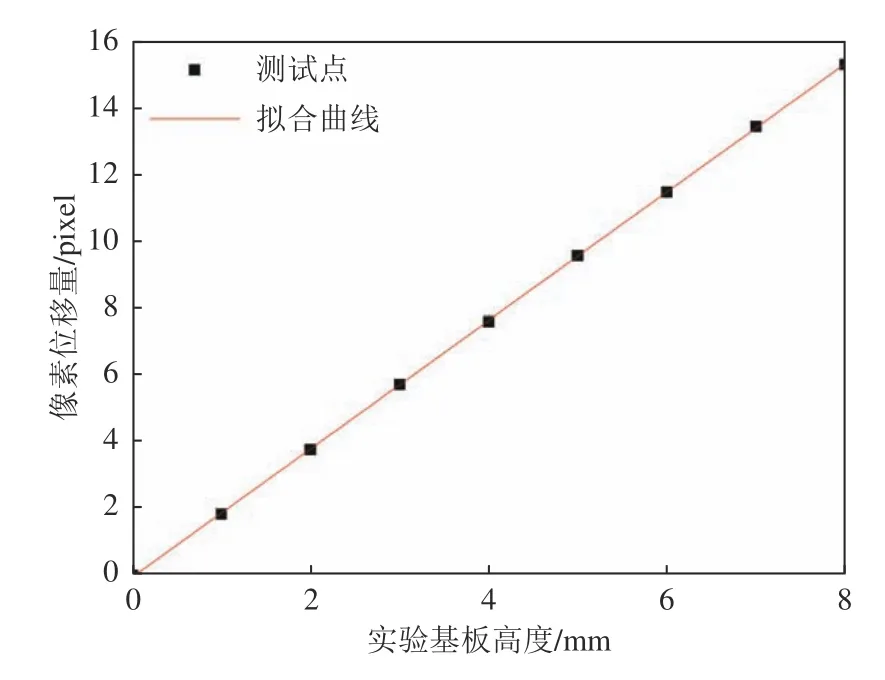
圖4 DIP 標定結果圖Fig.4 DIP calibration result diagram

2 DIP 技術測量平板水膜流動

2.1 實驗臺

圖5 為平板水膜流動實驗臺。風道氣流經收縮段整流后進入實驗段，為保證氣流均勻，在收縮段上游設置蜂窩器和阻力網。實驗段橫截面為300 mm×75 mm。為方便更換實驗基板，實驗段頂部采用可拆卸的玻璃蓋板。實驗基板為拋光鋁材，其下裝有升降臺。實驗基板的一端開有出水槽，出水槽連接供水箱，供水流量通過高精度齒輪泵進行調節。

圖5 平板水膜流動實驗臺Fig.5 Flat water film flow test setup

2.2 實驗臺精度測試

為了測試DIP 系統的測量精度，使用DIP 系統測量了長寬高為1200.0 mm×1000.0 mm×0.5 mm 的實驗基板。首先對DIP 測量系統進行標定，得出系統的K值。隨后獲取參考圖像和測試圖像，使用圖像互相關算法計算參考圖像與測試圖像之間關注點的位移量。最后，根據K值和位移量計算得到實驗基板的高度分布。圖6（a）給出了實驗基板高度h'分布的DIP 測量結果。實驗基板的高度分布已知，DIP 系統的測量精度可以通過測得的高度分布與實際高度分布進行定量比較評估。DIP 測量誤差分布如圖6（b）所示。測量結果顯示，實驗基板中間區域測量誤差較小（2% 以內），上下兩側的測量誤差在2%～5%之間。這是由于投影儀的投影方向與攝像機采集方向需呈一定角度，而DIP 系統配置的攝像機垂直于實驗基板，因此，投影儀傾斜投射出的網格在實驗基板中部區域聚焦較好，網格點清晰，而兩側區域聚焦較差，網格點模糊，增大了測量誤差。此外，DIP 系統部件的搭建角度和攝像機分辨率的限制也是造成DIP測量誤差的主要原因。由DIP 測量原理可知，投影部件與攝像機部件之間的夾角越大，DIP 測量系統單位距離的網格點像素位移量越大，測量精度越高。受實驗條件的限制，本文DIP 測量系統的部件夾角為81°。在圖像互相關算法原理中，攝像機的分辨率越高，圖像互相關算法計算出的最終位移量精度越高。本文實驗攝像機的分辨率為4×106pxiel，拍攝區域面積為80 mm×120 mm。

圖6 實驗臺精度Fig.6 Test setup precision

為說明DIP 測量系統對毫米級高度測量的精度，本文在已搭建好的水膜流動實驗臺上使用DIP測量技術進行3 mm 高度范圍內的梯度測量。引入色散共焦位移計同時測量，將其測量結果作為參照。在圖3所示的實驗臺基礎上將色散共焦位移計垂直于實驗基板固定。由低到高等間隔升高升降臺，每次升高500 μm，共6 次。每次升高升降臺后，采集網格測試圖像并同時記錄色散共焦位移計測量結果。該實驗重復3 次，最終結果取平均值，如圖7所示。從圖中可以看出：兩種測量方式得到的結果均呈現出良好的線性趨勢；隨著測量高度增大，共焦位移計與DIP 測量系統的測量誤差均增大。相較于DIP 測量，共焦位移計的測量誤差隨著實測距離越來越大。這是由于共焦位移計有特定的測量距離范圍，當超出測量范圍時，共焦位移計不能很好地聚焦待測平面，導致測量距離越大、測量誤差越大；這也可以反映出在3 mm 高度范圍內，當測量高度較大時，DIP 測量技術的精度優于色散共焦位移計。

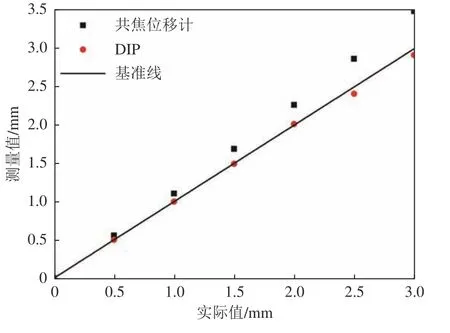
圖7 測量結果對比圖Fig.7 Comparison of measurement results

2.3 平板水膜流動實驗結果

在水膜流動中，水膜雷諾數定義為：

其中，Q為水膜質量流量，W為水膜潤濕寬度，μw為水的動力黏度系數。

在實驗中，流場風速Ua=17 m/s，水膜雷諾數Ref范圍為16.5～188.6。為增大水表面的反射性，在水中加入1%體積比的白色乳膠漆。通過落球法測試配置液體在溫度為20 ℃時的動力黏度μw=0.985×10–3Pa·s。在實驗段上部空間，使用Texas instrument DLP450 型投影儀投影方形網格圖像，同時使用PCO HS4 型高速攝像機采集圖像，采集頻率為100 Hz，曝光時間為1 ms。攝像機匹配鏡頭型號為定焦尼克爾105 mm。圖8 顯示了實驗基板水膜的參考圖像和變形的測試圖像，h為水膜高度。投影的單個方形網格尺寸為2.8 mm×2.8 mm，網格條紋寬度為0.8 mm。與參考圖像（圖8（a））相比，測量圖像（圖8（b））由于存在水膜而顯著變形。將參考圖片與測量圖片使用圖像互相關算法進行計算，計算過程中的關聯窗口設置為2.4 mm×2.4 mm 的方形窗口。圖8（c）展示了經過三維重構后獲得的水膜流過鋁板表面的高度分布。

圖8 實驗采集圖像與計算結果對比圖Fig.8 Comparison of test photo and calculation

本文開展了不同雷諾數下的水膜流動實驗，水膜高度的DIP 計算結果如圖9所示，L為水膜流動長度。整體上，水膜的高度隨著水膜雷諾數的增大而增大。水膜雷諾數在16.5～23.6 范圍時（圖9（a）和（b）），潤濕區域的水量較少，風速對表面波的傳導影響較大，此時水膜整體較薄，無法形成穩定的表面波傳導。隨著水膜雷諾數的增大（圖9（c）～（f）），潤濕區域內的水量逐漸增多，水膜在氣液界面剪切力的作用下形成表面波。隨著水膜雷諾數的增大，水膜表面波越來越向潤濕區域中心集中，中心潤濕區域的水膜高度越來越大。當水膜雷諾數繼續增大到165.0及以上時（圖9（g）和（h）），實驗設定的風速不能夠以穩定的表面波向后發展水膜。

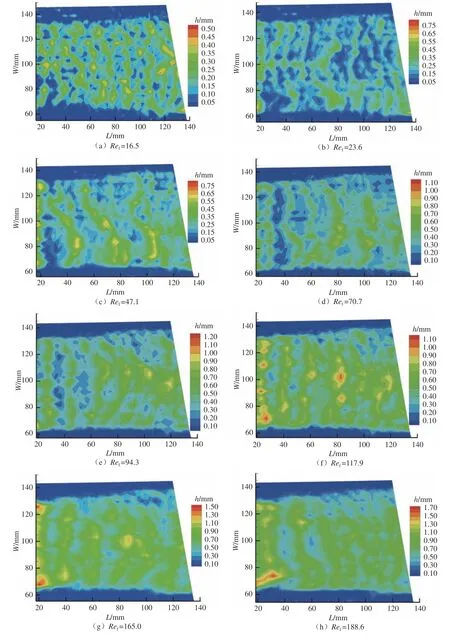
圖9 水膜流動DIP 計算結果（Ua=17 m/s、Ref =16.5～188.6）Fig.9 DIP calculation results of water film flow(Ua=17 m/s and Ref =16.5-188.6)

為了更好地研究水膜雷諾數對水膜表面波形的影響，分別取水膜雷諾數為16.5、70.7、188.6 的DIP計算結果的中間截面剖面曲線，如圖10所示。Ref=16.5 時，水膜表面波呈現出振幅小，周期短且不穩定的特性。Ref=70.7 時，潤濕區域內水膜的高度整體增大，水膜表面波振幅和周期均較穩定。Ref=188.6時，在水膜平均高度增大的同時，出現了表面波振幅較大、周期較長的現象。因此，在特定風速下隨著水膜雷諾數的增大，水膜表面波呈現出振幅逐漸增大、振動頻率逐漸降低的波動特性。

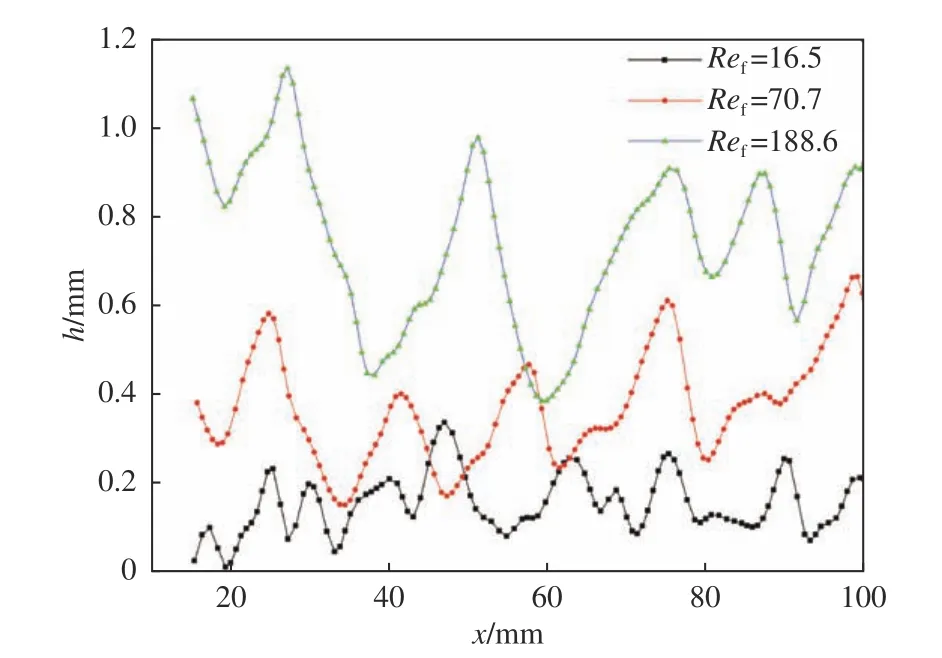
圖10 水膜剖面表面波形圖Fig.10 Water film surface wave profile

3 實驗模型驗證

3.1 平均水膜高度結果驗證

在水膜高度較薄、水流速度較低的條件下，水膜流動可簡化為二維不可壓縮層流流動。對Navier-Stokes 方程進行簡化得出水膜高度的關系式[3]為：

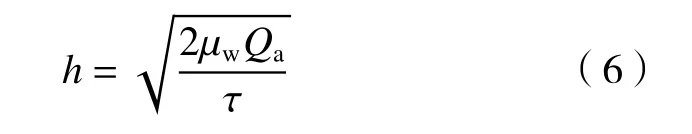
其中Qa為上游流入的單位潤濕長度水的體積流量，τ為氣?液界面剪切力。借鑒氣?液兩相分層流研究的經驗[17]，界面剪切力可以表示為：

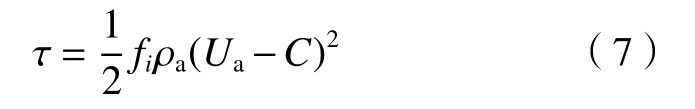
其中，fi為界面剪切系數，通過實驗結果測得；ρa為空氣密度；Ua為空氣主流速度；C為氣?液界面波的相位速度，由于C遠小于氣流速度，故在計算中忽略[18-19]。對于平板邊界層模型[20]，界面剪切系數fi=0.074(Rea)?0.2，其中Rea=UaH/υa為氣流雷諾數，υa為空氣運動黏度系數。通過式（6）和（7）可得水膜高度與水膜雷諾數之間的關系為：

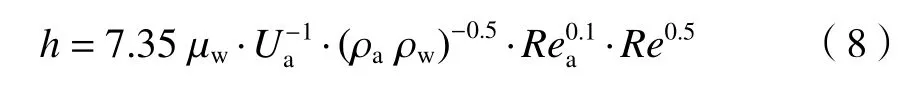
本文測量了8 個水膜雷諾數狀態下10 個時刻的水膜高度分布，并將結果平均化處理得到平均水膜高度。平均水膜高度hˉ與雷諾數的關系如圖11所示，用冪函數擬合得到其關系式為：

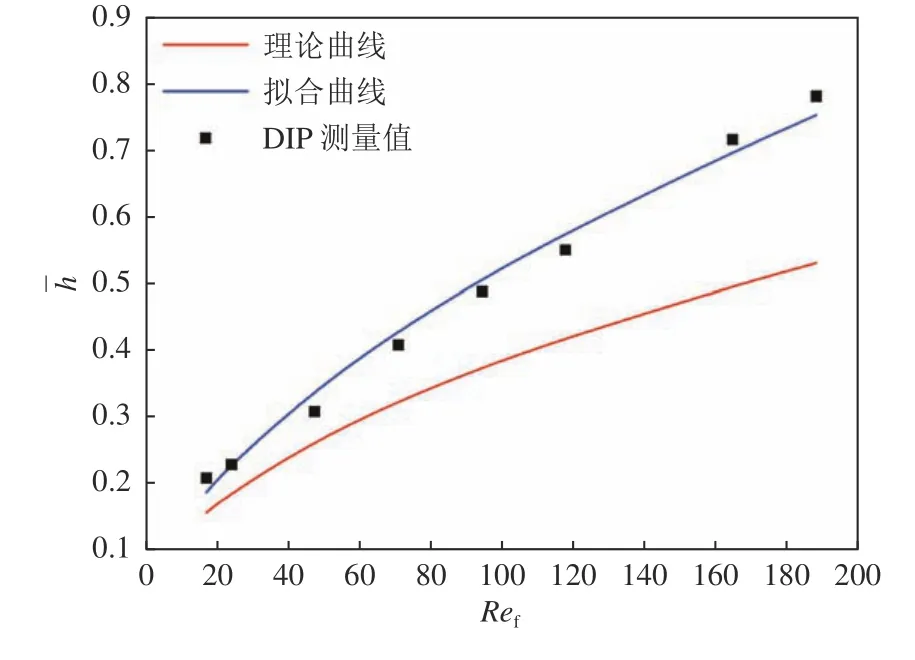
圖11 平均水膜厚度對比圖Fig.11 Comparison of average film thickness

如圖11所示，實驗得出的擬合曲線與理論推導曲線整體趨勢相近。但是水膜雷諾數的實測值略大于理論推導值，并且該趨勢隨水膜雷諾數的增大逐漸明顯。這是由于隨著水膜雷諾數的增大，水膜的流速增大，水膜流速增大到一定程度時形成的表面波為滾動不穩定狀態。此時水膜的表面波將影響氣?液界面剪切力τ的計算，隨水膜雷諾數增大而增大，理論推導曲線與實驗曲線差別逐漸增大。因此，當水膜雷諾數增大到一定程度時，需考慮水膜表面相位速度對水膜高度的影響。此外，本文的理論曲線基于一系列假設推導得出，這對比較結果也帶來一定影響。隨著水膜雷諾數的增大，水膜高度增大，DIP 投影網格清晰度降低，加大了圖像互相關算法的誤差，這也使得圖像處理結果誤差增大。

3.2 無量綱水膜高度結果驗證

為進一步驗證DIP 測量技術應用于平板水膜流動的可靠性與準確性，特引入無量綱水膜高度。將平均水膜高度與剪切應力相結合進行無量綱化，定義水膜無量綱高度h+為：

表1 列出了以往文獻及本研究的無量綱水膜高度的計算模型，其中Kosky & Staub 模型[21]為水平冷凝環狀流模型，Rishikesan 模型[4]為基于色散共焦位移計測量的平板水膜流動模型，Hughmark 模型[22]為等溫條件下的上升流模型。與前兩者比較，Hughmark 模型將氣?液兩相的質量流速、管直徑和流體的物理性質作為研究變量來預測水膜高度，本文預測模型與之類似。各模型計算值結果如圖12所示。可以看出，雖然本文研究對象與Rishikesan 模型的研究對象均為平板水膜流動，但是本文使用的DIP 測量方法與Rishikesan 模型的單點共焦位移計測量方法最終測量誤差存在差別（如圖7所示），從而導致這兩種模型存在偏差。本文測量水膜高度方法雖與其他文獻的測量方法不同，但應用到水膜無量綱高度的模型中，與其他研究模型計算結果的趨勢具有良好的一致性，更為接近Hughmark 模型，誤差在5%以內。

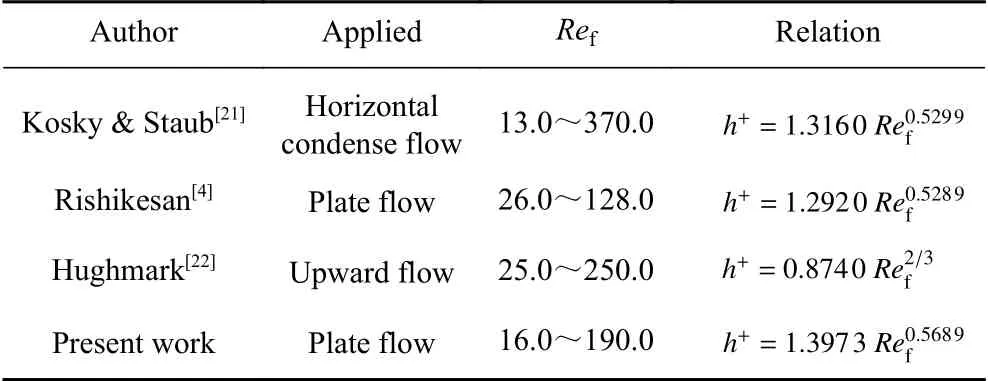
表1 無量綱水膜厚度模型Table 1 Dimensionless Film Thickness Models

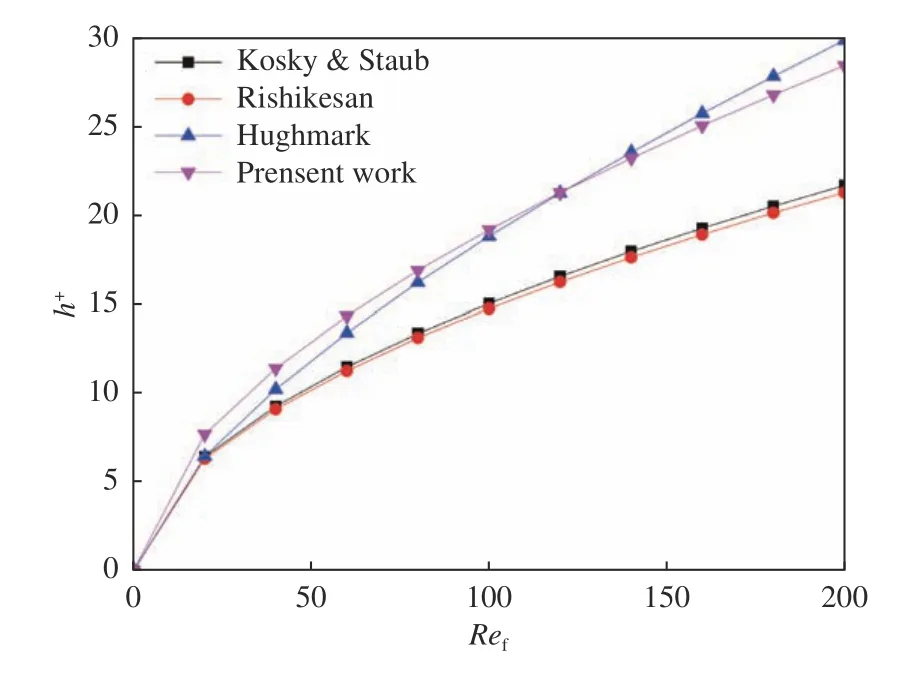
圖12 無量綱水膜厚度對比圖Fig.12 Comparison of Dimensionless Water Film Thickness

4 結論

本文介紹了可實現非侵入定量測量的DIP 技術，說明了其測量原理、標定方法，并將其應用于平板表面水膜流動的定量測量，最后將測量結果與理論推導和文獻結果進行對比得到以下結論：

1）DIP 測量技術可對流體流動的三維全貌進行復原。本文復原了平板水膜表面波隨雷諾數的形態變化。

2）DIP 測量技術擁有良好的精度。在本文的實驗臺參數設置下，DIP 系統的測量誤差小于5%。高度在3 mm 以內的測量，DIP 測量技術精度優于色散共焦位移計。

3）平板水膜流動實驗結果顯示：在風速17 m/s狀態下，隨著水膜雷諾數的增大，平均水膜高度整體增大；當水膜雷諾數增大到一定程度（Ref>165.0），水膜向中間聚攏，呈現出中間區域高于兩側區域的現象。隨著水膜雷諾數的增大，水膜表面波呈現出振幅逐漸增大、振動頻率逐漸降低的波動特性。

4）測量與理論推導發現：水膜表面波相位速度的定量測量是影響本文平均水膜高度測量的關鍵因素，會導致實測值與理論推導值的差別隨著水膜雷諾數的增大而增大。

5）無量綱水膜高度與水膜雷諾數的關系模型與文獻中的模型吻合良好，再次證明了DIP 技術在流體薄膜測量中的可靠性與準確性。