關于采樣問題的量子優越性綜述*

黎穎 韓澤堯 黎超健 呂勁 袁驍 吳步嬌?

1) (北京大學物理學院,北京 100871)

2) (北京大學前沿計算研究中心,北京 100871)

3) (廣東工業大學計算機科學與技術學院,廣東 510006)

利用量子態的疊加性和糾纏,量子計算為顯著地加速經典算法,例如大數分解、求解線性方程組、量子多體系統模擬等問題,提供了可能.隨著量子計算機硬件的快速發展,探索量子計算超越經典計算極限方向的研究受到了越來越多的重視.針對一類特定的問題,現有的量子設備已經展現出超越經典計算機的能力.但由于一些量子算法(諸如大數分解等問題)需要依賴于一個通用的大規模的容錯的量子計算機,考慮到現階段的量子設備的量子比特數十分有限,且容易與環境發生退相干,近期的研究主要集中在探索基于含噪聲的中等規模量子設備以及淺層量子線路的量子優越性.一些采樣問題被作為演示量子優越性的候選項提出.本文介紹和總結了幾個可以在現階段的量子設備上實現的量子優越性問題,并就其中兩個備受關注的量子優越性問題—隨機量子線路模擬和玻色采樣及其衍生的采樣問題的理論和實驗進展、經典模擬算法等展開討論.隨著上述兩類量子優越性問題在超導和光學量子平臺的實現,我們預期當前和近期的量子設備將解決更多問題,從而實現更一般的量子優勢.

1 引言

一些重要的諸如Shor 算法的例子預示了量子計算機相較于經典計算機具有更強的能力[1,2].但這些一般量子算法的實現需要具有數千邏輯量子比特或數百萬物理量子比特的通用量子計算機[3,4].而目前最先進的量子設備遠不能達到運行這些算法的要求.除了量子比特的數量遠遠不夠外,目前的量子設備還存在著兩個關鍵的不足:1)單個量子門的誤差;2)量子設備與環境的退相干作用.為了有效地闡釋量子計算機和經典計算機相比的優勢所在,Harrow 和 Montaro[5]形式化地定義了量子優越性問題需要滿足的4 個條件(以及一個可選的條件):1) 一個具有良好定義的計算問題;2) 一個可以求解該問題的適用于當前量子設備的量子算法;3) 任何經典模擬器需要超大規模的時間和空間;4) 復雜性理論的假設支持.除以上4 個條件外,另一個可選的條件為:存在一個可以有效區分量子算法和經典競爭者使用有限資源的輸出結果的方法.近些年來,一些采樣問題被作為量子優越性的候選項提出.

廣義的采樣問題是指得到特定分布的一個樣本.于是可以由多次獨立采樣的結果得出樣本背后分布的性質.在量子采樣問題中,在指定測量基矢下,經過一個量子過程后得到的最終的量子態可以被視為基矢的特定分布,因此,對該量子態的一次測量就對應一次采樣.本文討論的具有量子優越性的采樣問題包括隨機線路的采樣問題[6,7]、瞬時量子多項式線路的采樣問題[8]、玻色采樣[9]及其衍生出的問題[10-13],以及含有一個干凈的量子比特的高混合的確定性量子計算(DQC1)[14-16].理論上,這些采樣問題在基于一定復雜性假設下都是經典求解困難的.

隨機線路采樣隨機量子線路是指:一類構造為單量子比特門層和雙量子比特門層交替出現的量子線路,其中單量子比特門層中的比特門具有一定的隨機性,但單比特和多比特門的排放位置固定的一種線路簇,而一次采樣則對應于對一個容易制備的量子初態(通常是全 0 態),經過隨機線路后在計算基下進行一次測量,即采樣.在隨機線路采樣這一量子優越性問題的進程中,Boixo 等[6]提出了一個特定網格結構的量子隨機線路采樣問題,并估計當量子設備在有接近50 個量子比特時,經典計算機即無法有效模擬該電路,從而預計50 個量子比特的量子超導處理器即可以實現量子霸權.因為當下的量子計算機的噪音和退相干作用,該文獻也論述了如何去驗證量子設備采樣的可靠性.隨后,Arute 等[7]實現了53 個量子比特—懸鈴木處理器的20 層隨機量子線路,并在其上展示了量子優越性的采樣實驗.懸鈴木處理器可以在200 s 的時間內以0.2%的保真度采樣百萬量級次一個量子電路.中國科學技術大學潘建偉團隊[17]實現了66 個量子比特的超導設備—祖沖之2.0,當66 個量子比特全部運行時,可達到單比特門的誤差平均值為0.14%,兩比特門的誤差平均值為0.76%,讀取誤差的平均值為4.77%.為了驗證該設備的有效性,他們在其上執行了56 個量子比特,20 層的隨機線路采樣實驗.最近,該團隊又在祖沖之2.0 的基礎上升級了祖沖之2.1 超導量子芯片,把平均讀出保真度從95.48%提高到97.74%,并在祖沖之2.1 上實現了60 個量子比特24 層隨機線路的采樣實驗[18].對于隨機線路采樣問題,是否存在有效的經典模擬器也受到了廣泛研究.針對Boixo 等[6]提出的隨機線路的特定結構,Iboldsymbol 團隊[19]利用張量網絡的方法,在Iboldsymbol 的超算上計算出了 7×7 量子比特、深度為27 層的隨機線路的所有振幅,以及 7×8 量子比特、深度為22 層的部分振幅.之后,Google 團隊[20]利用馮諾依曼路徑的方法,在Google 云平臺上實現了 7×8 量子比特、深度為30 層的 2×105個振幅的計算.與此同時,阿里團隊[21]提出,他們可以利用一個分布式經典模擬算法,在阿里云平臺上實現 8×8 量子比特、深度為40 層的一個振幅的計算,以及9×9×40,10×10×35,11×11×31,12×12×27的一個振幅的計算(這里l1×l2×d表示l1×l2的量子比特上的深度為d的電路).Li 等[22]通過將張量網絡和“隱分解”的方法相結合,在太湖之光上實現了7×7量子比特、深度為39 層的全振幅的計算,以及深度為56 層的一個振幅的計算.本源量子團隊[23]估算他們可以在16 天內針對該類型電路實現72 比特,22 層的一次采樣.Chen 等[24]在神威上進行模擬,可運行一維鏈上的1000 量子比特以及二維 125 × 8 量子比特 42 層一個振幅的計算,72量子比特32 層(2D-Bristlecone)的隨機量子線路的一次采樣.阿里團隊之后又在文獻[25]中提出他們可以對Bristlecone-70 結構(70 量子比特) 1 +32+1 深度的隨機線路,通過阿里云平臺在0.43 s內求出任意振幅(以及70 量子比特1+36+1/1+40+1 深度采樣時間5.6/580.7 s).這里需要注意的是全振幅的模擬可以用來生產若干次采樣的樣本,另一方面,一次采樣也可以利用蒙特卡羅等方法通過計算少量次振幅進行估計.

針對Arute 等[7]提出的53 量子比特的量子計算機,Iboldsymbol 團隊[26]在2019 年針對該問題設計了經典模擬采樣算法,并通過小的樣例估計出在Summit 超算上可在少于2.55 天的時間內得到20 層的采樣,以及6.45 天內得到36 層的采樣.之后阿里團隊[27]在2020 年針對該電路采樣問題,進行經典模擬,并在阿里云上進行測試,可在少于20 天的時間內實現該問題的模擬(42 層,保真度0.2%).近期文獻[28]通過一種張量網絡方法可以只用60 GPU 在5 天內模擬(20 層,保真度73.9%).

瞬時量子多項式線路的采樣和隨機線路采樣類似,瞬時量子多項式線路的采樣也是針對一種特定結構的量子線路的采樣,與隨機線路不同的是,瞬時多項式線路除了第一層和最后一層外,中間層都是由對易的對角門構成,因為是對易的,所以中間的所有門可以通過任意的時間次序執行,這也解釋了這里的“瞬時”的含義.Shepherd和Bremner[8]介紹了一個量子優越性問題—瞬時量子多項式(instantaneous quantum polynomial time,IQP)協議.IQP 協議是一個受限的,非通用的量子計算模型.該協議可以被視為是一個兩體的經典通信信道.Alice 設計了一個經典不可解的問題,并擁有一個可用來驗證結果的正確性的隱變量.Bob 用Alice 的輸入執行IQP 線路(一個多項式深度的電路).最終,Alice 通過結合協議運行的時間以及收到結果的正確性來論述量子霸權.Bremner 等[29]證明了IQP 線路的計算即使以41%的乘法性近似也是經典模擬困難的.之后Bremner 等[30]進一步證明了在基于一些額外的復雜性假設下,該問題的加法性近似也是經典模擬困難的.IQP 協議后來被推廣到量子計算的連續變量(continuous variable,CV)模型中[31,32].

玻色采樣玻色采樣(boson sampling,BS)是建立在光學系統上的一個量子過程.標準的BS 是在線性光學網絡的輸入端的前n個模中每個注入一個光子,該線性光學網絡的元器件的組件系數具有一定的隨機性,并在輸出端對光子數進行采樣.Aaronson 和Arkhipov[9]在2011 年提出了將BS 作為量子優越性的一個候選項問題.BS 的原型[9]需要用到一個線性光學網絡裝置.因為該原型需要制備很多個高品質的單光子,實驗上實現該過程也很困難.后來Lund 等[10]在此基礎上提出了散射玻色采樣(scattershot boson sampling,SBS),該模型解決了初始模型單光子制備比較困難的問題,但卻需要一個額外的裝置及測量過程來確定輸入的光子模式.之后SBS 模型被進一步進行了改良[11],即高斯玻色采樣(Gaussian boson sampling,GBS).GBS 之后被推廣為振動玻色采樣[33],該模型是在BS 的啟發下對分子譜的研究.GBS 利用單模壓縮態(single-mode squeezed states,SMSS)作為輸入,且不需要通過額外的裝置和測量來確定輸入態.需要強調的是,雖然GBS 是為了降低標準玻色采樣和SBS 實驗的困難性提出的,但目前仍然缺少嚴格的復雜性證據證明該過程是經典計算難的.然而,有充分的理由相信該問題的確是經典計算困難的,因為Hafnian 問題(GBS 的輸出概率和矩陣的一個函數Hafnian 相關)可以作為積和式的推廣代入玻色采樣中,即可得到GBS.除此之外,GBS 有很多應用,比如求解圖上的一些理論問題[34-37]、近似優化問題[38]、分子對接問題[39]、點處理問題[40]等.考慮到GBS 模型輸出端收集每個模中的光子數的困難性,Quesada 等[41]提出了帶閾值的GBS 模型,該模型和GBS 模型的區別是在接收端只是探測有無光子,并不對光子數進行計數,他們在文章中也論證了該模型的計算困難性.最后,上海交通大學的金賢敏團隊[13]近期也提出了時間戳玻色采樣.

玻色采樣及其衍生問題在實驗上也取得了顯著的進展[42-51].特別地,Wang 等[51]最近實現了在60 個模中注入20 個光子的干涉儀.Bentivega等[52]實現了第一個SBS 實驗,其中6 個不同的光子對整合到光子電路中.Zhong 等[49]實現了第一個GBS 實驗,其中以很高的采樣率實現了5 個光子的GBS.Su 等[48]通過使用光子數分析探測器,可以將高斯態轉變為非高斯態,并給出了使用GBS設備實現的非高斯態的制備.值得關注的是,近期潘建偉團隊[53]實現了一個100 個模的線性光學網絡—九章,并在其上執行了帶閾值的高斯玻色采樣實驗,實驗成功地在67 個模中觀測到光子.

玻色采樣及其衍生問題的經典模擬在近些年也取得了一定進展.Neville 等[54]通過Metropolis獨立采樣方法,可以得到玻色采樣的一次近似采樣,他們可以在普通筆記本上實現30 個光子的一次近似采樣,在超算上可以實現50 個光子的一次近似采樣.并通過和其他采樣算法(包括暴力采樣、拒絕采樣方法)作比較,來證明該近似采樣算法的正確性.Clifford 和Clifford[55]給出了一個θ(n2n)時間、多項式空間的一個精確采樣算法,其中n是光子數.Wu等[56]提出了一個O(poly(n)28n/3)時間、多項式空間的GBS 模擬采樣算法,其中m是模數,n是光子數,r是壓縮參數.當有指數規模的計算空間時,可以進一步將時間復雜性提升到.可以在華為昆侖服務器上實現20 個光子的采樣,并通過模擬預測可在神威超算上實現30 個光子的采樣.Quesada 等[41]針對帶閾值的GBS 模型給出了一個O(mn2n) 時間復雜性的一個經典模擬算法,并在文獻[57]中對GBS 進行了經典模擬,他們的算法可以在56 個CPU 的云上進行20 個光子的精確采樣.

量子隨機線路采樣作為量子霸權的候選項之一,近幾年來備受關注.這一方向的超導量子設備在不斷地更新,經典無法超越量子的趨勢也越來越顯著.Iboldsymbol 更是計劃在2023 年實現1000量子比特的量子計算機.相信在未來的某一天,當量子隨機線路的規模和精度各自達到某個閾值時,人們將無法再找到可以在幾個小時內甚至幾年內在經典計算機上進行有效模擬的算法.而在玻色采樣及其衍生物實驗中,近期潘建偉團隊[53]在基于光學器件搭建的實驗平臺上實現的高斯玻色采樣至今仍無經典計算機可以有效模擬,也充分顯示了量子優越性的里程碑進展.

本文組織如下,第2 節介紹3 種量子優越性相關的采樣問題.由于IQP 電路的采樣受到的關注較少,在第3 節和第4 節介紹實驗進展和經典模擬進展時,只討論了量子隨機線路采樣和玻色采樣的進展.第5 節總結和討論量子優越性的現狀和未來.

2 優越性的問題簡介

本節主要介紹量子隨機線路的采樣、IQP 電路采樣和玻色采樣問題需要處理的具體任務.

2.1 量子隨機線路采樣

2.1.1 方案介紹

在量子計算機上,采樣就是對隨機線路進行測量.而經典計算機上則對應的是計算輸出的希爾伯特空間上的概率分布上的一次采樣.隨機線路的采樣在經典計算機上進行模擬被認為是困難的(沒有多項式時間的經典算法能夠做到)[58].而對量子計算機本身,要實現大規模高深度的計算也對硬件的容錯率提出了很高的要求.因此量子電路的結構設計需要考慮到超導硬件的設計,以及支持的簡單門操作類型.下面介紹兩個特定結構的隨機線路的模型.

Boixo 等[6]提出的隨機線路模型如下:

· 執行一層H門.

· 重復d輪下面兩步操作.

1)交替地執行一次圖1 中的CNOT 門,這里一個黑點代表一個量子比特,兩個黑點之間的連線表示這兩個量子比特有門作用.

這里X,Y依次為Pauli-X門和Pauli-Y門.令At:=e-itA/2.根據該定義可得圖1 中X1/2和Y1/2門的定義.

圖1 隨機線路的CNOT 門的8 種不同的擺放方式[6].其中第0 層全部擺放H 門,電路中每8 層循環一次(重復圖中1—8 層),空白節點處隨機放置 I,T,X1/2,Y 1/2 門,兩比特門為CZ 門Fig.1.Eight different layouts of the CNOT gate in the random circuit,where all of qubits are performed H gate in the 0 -th layer,and cycle once every 8 layers in the circuit (repeat 1—8 layers of this graph),the blank vertices are laid out I,T,X1/2,Y 1/2 randomly,and the two-qubit gates are all CZ gates[6].

隨機線路采樣是從這樣的一個隨機線路中進行一次采樣(在電路結束時對電路在計算基下進行測量).如果想要體現量子的性質,這里深度d需要滿足一定要求.理想的量子隨機線路采樣的輸出分布的概率值滿足Potor-Thomas 分布,Boixo 等[6]通過模擬實驗展示了在深度超過20 層時,量子電路輸出的概率值跟Portor-Thomas 分布逐漸開始靠近.

Google 團隊在2019 年提出了一個更大規模的網格結構,門的擺放更復雜的量子隨機線路模型—懸鈴木量子計算機,并且在量子設備上進行了測試,可以在幾秒內實現53 個量子比特,20 層兩比特門的隨機線路保真度至少為0.2%的采樣,該隨機線路結構如圖2 所示[7].

圖2 懸鈴木處理器隨機線路架構[7].其中第0 層全部擺放H 門,電路每層迭代重復模式ABCDCDBA,兩個模式中間由一層隨機放置的單比特門 X1/2, Y 1/2, W1/2 構成,兩比特門為控制相位門和部分 iSWAP 門的乘積(部分 i SWAP 門后跟隨一個控制相位門構成)Fig.2.Random circuit architecture for Sycamore processor,where all of qubits are performed H gates in the 0 -th layer,the layer of the circuit iterates and repeats the pattern ABCDCDBA,a layer of random single-qubit gates are performed between two modes,which constructed by X1/2, Y 1/2, W1/2,the two-qubit gate is the multiplication of the partial-iSWAP gate and control-phase gate (constructed by partial-iSWAP gate followed by a control-phase gate)[7].

因此,在Google 提出的隨機量子線路采樣問題框架中[6,7],隨機量子線路U是由一系列電路層組成的,每層電路在一組單比特和雙比特門中按照一定的限制隨機地選取一系列門,電路層的深度為d時,產生的分布為pU(x)=|〈x|ψd〉|2,其中x是計算基下的比特串.

隨后,中國科學技術大學潘建偉團隊[17]實現了一個規模更大的66 量子比特的超導設備—祖沖之2.0 處理器.該處理器的結構也是網格狀結構,研究團隊在其上實現了56 個量子比特,20 層的隨機量子線路采樣實驗.在祖沖之2.0 基礎上升級的祖沖之2.1 的平均讀出保真度由95.4%提升到了97.74%,潘建偉團隊在祖沖之2.1 上實現了60 量子比特24 層深度的隨機量子線路[18].

2.1.2 隨機線路采樣的基準

Boixo 等[6]通過交叉熵差別(cross entropy difference)論述了他們提出的網格上的量子線路采樣的正確性.他們展示了當電路可模擬時,其交叉熵可以被高效地通過測量估計出.當經典計算機無法有效模擬時,可以通過將電路劃分為若干子部分分別進行模擬來對交叉熵進行估計,從而對輸出結果的正確性進行測試.接下來簡述一下量子優越性的基準—交叉熵的定義.

首先,令|ψ〉=U|0〉為一個給定的隨機線路U∈C2n×2n的輸出態.考察樣本集合S={x1,···,xm},其中xi是一個長度為n的二進制串,通過對|ψ〉的每個量子比特在計算基下進行一次測量得到.令pA(x|U) 表示滿足由算法A構造出的分布中樣本x ∈{0,1}n出現的概率,其中算法A構造的分布是對U|0〉在計算基下展開的分布的模擬,pU(x) 表示x的精確的概率值.pA(x)和pU(x) 之間的交叉熵定義為

Boixo 等[6]論述了如果該 7×7 網格的隨機線路深度足夠大,則pU(x) 的分布接近Porter-Thomas 分布Ne-Np,這里N=2n為態空間大小.因此,在對該隨機線路采樣的優越性進行驗證時,他們通過對實驗測量結果所得的分布和Porter-Thomas 分布進行比較,判斷該輸出的分布是否真實有效.實際計算該交叉熵時,通常是通過采樣得到的包含m個樣本的集合S來對其均值進行估計.此外,他們定義了一個用于衡量算法A采樣正確性的量—交叉熵差別:

這里算法A既可以是多項式時間或者指數時間的經典模擬算法,也可以是量子設備實現.如果算法A輸出的樣本滿足均勻分布,ΔH(pA)=0,如果算法A能夠真實還原出pU(x) 的理論分布,ΔH(pA)=1.Boixo 等[6]提出通過判斷交叉熵差別是否大于0 來判斷其量子效應.注意到這里為了得到交叉熵差別,需要一個強大的經典計算機來得到pU(xj) .

在驗證懸鈴木處理器輸出結果的正確性中,Arute 等[7]提出利用線性交叉熵作為基準的保真度.該線性交叉熵定義為

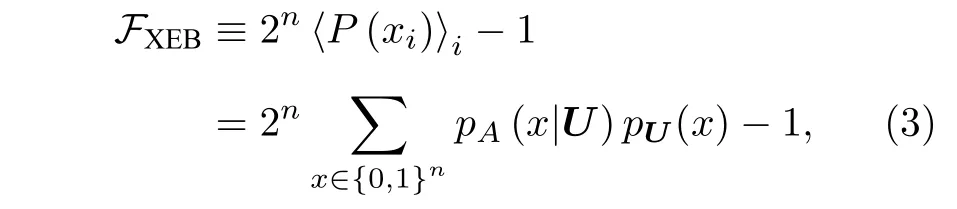
其中n是量子比特的數目,P(xi) 是理想的量子電路測得xi的概率,且這里的xi是利用算法A(算法A可以是實驗觀測)得到的二進制串.如果實驗沒有任何誤差,對實驗結果進行采樣得到的平均值FXEB=1.如果實驗輸出的是一個均勻分布,此時FXEB=0.對于實際的量子設備,FXEB是一個介于0—1 之間的數.這里需要注意的是,給定一個xi,P(xi)的值只能通過經典模擬該量子線路進行計算.因此,由于量子優越性問題的困難性,當線路規模足夠大時,FXEB是無法在有效的時間內計算得到的,因此需要近似的方法對FXEB進行估計.比較(2)式和(3)式可知,線性交叉熵和交叉熵差別的唯一區別是這里直接用概率替換了原來的對數項.

Arute 等[7]說明了當保真度大于32%時,(對數)交叉熵區分具有更小的標準差,反之當保真度小于32%時,線性交叉熵具有更小的標準差.由于驗證懸鈴木處理器的保真度較小,因此Arute 等[7]中采用的是線性交叉熵方法進行保真度的分析.Aaronson 和Gunn[59]證明了與線性交叉熵相關的一個判定量子優勢的問題無經典多項式時間算法可以求解.

2.2 IQP 線路的采樣

一個IQP 線路是一個形式為C=H?nDH?n的量子線路,其中H是Hadamard 門,D是由n的多項式個對角門生成的一個對角矩陣[60].IQP 采樣問題是通過將C作用于初始狀態|0〉?n而產生的n位字符串上的分布p進行采樣,之后在計算基上測量每個量子比特(p表示初始無噪聲分布).當D是在集合:,T門;或者(2)Z,CZ,CCZ中均勻選取時,IQP 線路的采樣問題是經典模擬困難的.該困難性基于玻色采樣問題中的復雜性假設PGC (permanent of Gaussian conjecture)問題在IQP 下的對應.Fujii 和Tamate[61]使用量子容錯理論表明,在噪聲很小的情況下,IQP 線路的采樣問題仍是計算困難的.

以上的IQP 線路允許門在系統中的任何量子位之間應用.這意味著D滿足集合(1)的隨機線路中可能有O(n2) 個門,滿足集合(2)的隨機線路可能有O(n3) 個門,其中許多是作用在非鄰接量子比特上的.從實驗的角度來看,特別是針對超導量子計算機,這是具有挑戰性的,因為超導量子設備的量子比特的作用都是局限在近鄰的.如果想要將非鄰接量子比特上的門調整到鄰接量子比特上執行,需要增加SWAP 門,但一個問題是IQP 線路中不允許有SWAP 門.于是最近Bremner 等[62]提出了稀疏的IQP 采樣,該稀疏的IQP 采樣與一個稀疏圖相關,且其采樣在一定復雜性假設下仍是計算難的.已經被證明,稀疏的IQP采樣在有O(nlogn)長度個門或者深度為時,在二維的格點結構下就可以證明其計算難需要的一個關鍵復雜性假設.

2.3 玻色采樣及其衍生問題

繼Aaronson 和Arkhipov[9]提出玻色采樣問題后,為了使得該問題更容易在實驗上實現,有很多更容易在實驗上實現的衍生問題相繼被提出.

2.3.1 玻色采樣

原始的玻色采樣問題[9]可以描述為:n個無相互作用、不可分辨的玻色子,在單粒子希爾伯特空間維數為m的Fock 空間中,從某個給定的初始狀態開始,經過確定的演化,在末狀態進行投影到占據數表象基上的測量,每次測量獲得一個n玻色子態,即稱為進行了一次玻色采樣.在初始條件、演化給定的情況下,采樣結果將服從一個確定的概率分布.

以實現玻色采樣實驗最常用的平臺—線性光學平臺為例,如圖3 所示,將n個單光子由波導輸入一個線性光學網絡中,該網絡中可能存在不同波導模式間的互相疊加、干涉等,所以也被稱作干涉儀,并可在輸出的m根波導中探測到光子.在理想情況下,每根波導僅能攜帶一種模式,輸入態到輸出態演化可以在占據數表象下記為

圖3 玻色采樣模型[56].輸入是 n 個單光子,經過線性光學網絡后,可在輸出的 m 個模中探測光子Fig.3.Device of boson sampling[56].The input aren photons,and one can detect photons on the m output modes through a linear optical network.

其中bj,aj分別對應m個輸出模式/輸入模式光子的湮滅算符.由于玻色子在這個過程中無相互作用,整個Fock 空間中多體態的演化算符W(即輸出態服從|Ψout〉=W|s1,s2,s3,...,sm〉)可以由單粒子的演化算符U完全確定,故采樣得到的分布也可以顯式計算得到.Aaronson 和Arkhipov[9]證明了

因此玻色采樣結果服從的概率分布為

其中,UST矩陣為將U矩陣的第i列重復si次、第j行重復tj次形成的一個n維矩陣,perm 表示該矩陣的積和式,對于一個一般的n維方陣A,積和式定義為

應當注意,一個能夠實現玻色采樣的量子計算機,其“計算過程”即體現為多體玻色子態的制備、演化以及最終測量的過程;另外,高效地實現玻色采樣并不意味著能夠高效地計算積和式,具體來說,光子數/模式數的增多將使得輸出端測量得到某一給定狀態的概率大幅下降,即“采樣率”很低,進而通過計數某種輸出狀態的頻率來準確估計相應積和式的值也變得非常困難;玻色采樣過程可以看作是量子光學中Hong-Ou-Mandel 實驗的擴展,從而,類似于Hong-Ou-Mandel 實驗,不同模式光子之間不可忽略的量子干涉現象導致的巨大的多體希爾伯特空間維數是實現量子霸權的先決條件,而這對U矩陣的形式提出了要求,即U的形式過于簡單將導致該玻色采樣過程成為經典計算機可以有效模擬的,一般認為,酉演化U矩陣的選擇應當服從隨機酉矩陣的Haar 測度,即只要U足夠任意,便認為其可以實現量子優越性.

2.3.2 高斯玻色采樣

玻色采樣提出后,受制于確定性單光子源制備等難點,其實驗實現一直停留在小規模展示階段,難以達到實現量子優越性要求的n ≈50 界限.與此同時,一些基于玻色采樣的理論工作被相繼提出,例如容許光子損耗的玻色采樣(lossy boson sampling)[12],輸入n+k個光子,但后選擇出n個光子的輸出態,即容許k個光子的損耗,由于對該過程的理論分析依賴于對損耗過程的理解,所以對其能夠實現量子優越性的閾值分析仍然有待解決.

在另外一些工作中,研究者關注于利用非確定性的、更高效、易于制備的光子源,以擴展原始的玻色采樣,達到實現量子優越性的目標.如 Lund等[10]提出了后來被稱為SBS 的方案,如圖4 所示.使用m模的線性光學網絡,將m個概率型光子源分別置于其輸入端,每個光子源將產生處于雙模壓縮態的光子(區別于單光子源的輸入態具有確定的光子數,由于其光子數的概率分布特性,也被稱作高斯態的一種),利用雙模壓縮態的特性,可以設計光路,在輸出端后選擇出n光子的測量事件,但是,這一方案的輸入輸出均有種可能,導致了采樣空間的大幅增長.

圖4 SBS 的裝置簡介[63].該模型中輸入為 2m 個單模壓縮態,在其進入分束器和相移子裝置后產生雙模壓縮態,并通過一個額外的測量裝置來固定SBS 的線性光學裝置Um 輸入的光子數Fig.4.Brief introduction of SBS device[63].In this model,the input are 2m single-mode compressed states,and the two-mode compressed states are generated after entering the beam splitter and the phase-shifting sub-device.An additional measuring device is used to fix the number of input photons for the linear optical device Um of SBS.

Kruse 等[63]隨后注意到了SBS 方案的缺陷:該方法利用了概率型的光子源,但其后選擇過程卻拋棄了光子源的概率特性.他們據此提出了GBS 的方案(圖5),去掉了SBS 方案中的后選擇過程,直接將單模壓縮態注入干涉儀,并在輸出端進行光子數測量,他們證明了,輸出態測量得到光子數S= (s1,s2,···sm) 的概率為

圖5 GBS 的裝置簡介[63].輸入端為K 個單模壓縮態注入線性光學網絡,在輸出端的M 個模中進行光子數探測Fig.5.Brief introduction to GBS device[63].The input terminal is a K single-mode compressed state injected into the linear optical network,and the photon number is detected in M modes at the output terminal.

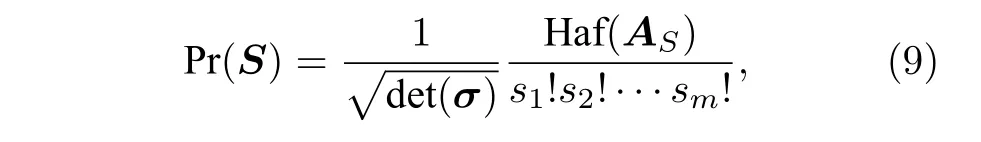
其中AS是分別取A中i行/列和第m+i行/列si次得到的矩陣,矩陣A定義為

Haf 表示Hafnian 函數,矩陣的Hafnian 函數定義為

其中Mn是 [n]:={1,2,···,n}中的所有完美匹配構成的集合,V(i,j)是V的第 (i,j) 個元素.例如,當n=4 時,M4={(12)(34),(13)(24),(14)(23)},其中 (ij) 是一個匹配對,因此

從定義來看,Hafnian 是排列不變量.交換V中的任意兩列,以及相同標號的兩行,得到的新矩陣的Hafnian 值保持不變.由Haf 的定義知,Haf 可以看作是積和式的擴展,即:

從而,任何能夠計算Hafnian 的算法也一定可以以同樣的復雜度解決積和式的計算問題,這一結果,使得高斯玻色采樣一經提出,便成為在線性光學體系實現量子優勢的有效方案.類似于積和式,精確地計算矩陣Hafnian 是 #P -hard 的[64],這暗示著具有相同壓縮參數的GBS 是經典計算難的,求解Hafnian 的經典最好的算法需要時間O(n32n/2)[65].

更進一步地,考慮到實驗上光子探測器實現光子數分辨的難度,即探測器很多時候只能準確判斷某個模式有/無光子,而不能判斷有幾個光子,基于這點,高斯玻色采樣可以被擴展為帶閾值的玻色采樣,Hafnian 將繼續擴展為Torontonian[41].帶閾值的玻色采樣也是最容易進行大規模實驗的方案.

Quesada 等[41]給出了帶閾值的高斯玻色采樣問題輸出結果S=(s1,···,sm) 的概率為

其中σ是協方差矩陣,AS是取A中與S相關的行和對應的列得到的矩陣,Tor 函數定義為

其中P([n])是集合 [n]={1,···,n}的一個指數集合(包含所有子集合的集合),是矩陣A∈C2n×2n的Torontonian 函數.

3 實驗進展

近幾年來,隨機線路的采樣和玻色采樣及其衍生的采樣問題在實驗上均已取得了顯著的進展.下面簡要介紹一下量子隨機線路和玻色采樣的近期實驗設計方案.

3.1 量子隨機線路采樣的實驗進展

2019 年,Google 團隊首次在Sycamore 超導量子平臺上實現了量子優越性[7].Sycamore 量子芯片上有 53 個可用的量子比特,86 個耦合器,量子比特和耦合器都用transmon 構成,利用微波激發量子比特,通過磁通調節耦合,通過連接的諧振器讀出量子態.Sycamore 的平均單比特錯誤率達到了0.15%,同時激發時也只略微高出一點,控制在0.16%;雙比特平均錯誤率為0.36%,同時激發時為0.62%;單獨讀出錯誤率為3.1%,同時讀出錯誤率為3.8%.通過簡單地把門操作和讀出操作的保真度相乘,可以估計系統的保真度.在該實驗中,最大的隨機量子線路有53 個量子比特,1113 個單比特門,430 個兩比特門,對每個量子比特進行一次測量,通過相乘的簡單模型估計系統的保真度可達到0.2%.交叉熵FXEB的不確定度為,需要百萬量級次抽樣(Ns)來從實驗上測定交叉熵.

交叉熵的測定需要對由超導隨機量子線路抽樣產生的百萬量級的比特串中的每一個給出理想分布下對應的概率幅,這個概率幅通過模擬隨機量子線路得到,但當隨機量子線路的規模過大、糾纏程度太高時,模擬隨機量子線路在事實上是不可行的,此時達到量子優越性區域.為了表征量子優越性區域的超導量子電路的保真度,Google 團隊在電路設計中采用了3 種、兩類線路.線路按照連接的完整度分為3 種:全量子線路、刪減量子線路、分割量子線路.其中全量子線路是2.1 節中描述的完整線路;分割量子線路中量子電路被切分為兩塊,兩塊之間沒有相互作用的量子比特;類似分割量子線路,刪減量子線路也對全量子線路里的雙比特門進行了一些刪減,使得線路成為相對獨立的兩塊,但是僅僅刪減了分割處的部分兩比特量子門,所以兩塊量子線路并不是完全獨立的.3 種不同完整度的量子線路的示意圖如圖6(a)左下角插圖所示.按照兩比特門的糾纏程度分為兩類線路,其中雙比特門排列為EFGHEFGH 的線路中雙比特門之間糾纏程度較小,更容易模擬,稱為簡單量子線路;而雙比特門排列為ABCDCDBA 的線路更難模擬,稱為復雜量子線路.簡單量子線路和復雜量子線路的示意圖分別如圖6(a)右上角和圖6(b)左上角插圖.

圖6 量子優越性證明的實驗結果[7] (a)在經典可驗證區,簡單全量子線路的保真度與簡單刪減量子線路、簡單分割量子線路、簡單乘積模型的保真度符合得很好,每個數據點是多個隨機量子線路采樣的平均值;(b)在量子優越區,通過更簡單的線路和簡單乘積模型來估計復雜全量子線路的保真度.紅色時間標志表示經典模擬復雜全量子線路的驗證任務需要的時間,灰色時間標志表示經典模擬相應的采樣任務需要的時間Fig.6.Experimental results of the proof of quantum advantage[7]:(a) In the classical verifiable region,the fidelity of simple full quantum circuit accords well with that of simple truncated quantum circuit,simple split quantum circuit and simple product model.Each data point is the average of multiple random quantum circuit samples.(b) In the quantum advantage region,the fidelity of complex full quantum circuits is estimated by using simpler circuits and simple product models.The red time label represents the time required for the verification task of the classical simulation complex full quantum circuit,and the grey time label represents the time required for the corresponding sampling task of the classical simulation.

Goolge 團隊在實驗中對量子線路層數為m=14 的簡單全量子線路、簡單刪減量子線路、簡單分割量子線路進行了采樣和模擬,如圖6(a)所示.在經典可驗證區域內,全量子線路保真度與相應的分割量子線路、刪減量子線路、簡單乘積預測的保真度符合得很好,所以在達到量子優越性的大規模復雜線路區域內,可以通過相應的分割量子線路、刪減量子線路和簡單乘積預測復雜大規模線路的保證度.在量子優越性區域內,53 量子比特的大規模ABCDCDAB 復雜量子線路的保真度隨著線路層數的加深而降低.實驗中最大的量子線路層數達到20 層,在10 個相同規模的隨機量子線路上進行了 30×106次采樣,用刪減量子線路估計的保真度達到FXEB=(2.24±0.21)×10-3.以5 西格瑪的置信度可以斷言在Sycamore 量子計算機上此類規模線路的平均置信度大于0.1%.實驗結果如圖6(b)所示.

估計經典計算機模擬需要消耗的計算資源時有兩種估計,一種是對驗證任務的計算資源的估計,一種是對采樣任務的計算資源的估計.如果實驗中對超導隨機量子線路進行了106次采樣,估計的保真度為0.1%,驗證任務需要用經典計算機計算出全部的 106次采樣得到的比特串對應的概率幅,而采樣任務只需要計算106×0.1%個比特串對應的概率幅,因為對于采樣任務而言,大部分平庸的采樣可以用均勻分布的背底表示.對于53 個量子比特的20 層的復雜全量子線路,在Sycamore上采樣一百萬次用了200 s,預計在一百萬核的經典計算機上通過Schr?dinger-Feynman算法進行模擬以產生相同保真度的采樣結果需要10000 年,而驗證任務則需要幾百萬年[7].

Sycamore 量子計算機對量子優越性的展示使得近期量子算法井噴式發展,與此同時,更高效的經典模擬算法也被提出來,使得量子優越性顯得不那么明顯.2021 年6 月,中國科學技術大學潘建偉團隊延續Google 團隊的工作,制造出了量子比特數更多、門控精確度更高的祖沖之量子計算機—祖沖之2.0[17].與Sycamore 類似,祖沖之量子計算機也是使用transmon 作為量子比特;與Sycamore相比,祖沖之量子計算機的量子比特數提高到66 個,單比特門的精度提高到99.86%,兩比特門的精度提高到99.41%,讀出精度提高到95.48%.該團隊[17]在祖沖之量子計算機上進行了最大規模為56 量子比特、20 層量子線路的復雜全量子線路隨機量子線路采樣,采樣一百萬個比特串耗時230 s,而實際實驗中在1.2 h 內進行了 1.9×107次采樣,通過與Sycamore 相同的估計方式估計出的祖沖之量子計算機在該規模下的保真度為(6.62±0.72)×10-4,在9 個西格瑪的置信度下斷言保真度不為0.用Schr?dinger-Feynman 算法模擬祖沖之量子計算機實現的最大規模采樣任務需要 5.76×1017核時,而用相同算法模擬在Sycamore 上實現的最大規模采樣任務只需要 8.90×1013核時;用更高效的張量網絡模擬方法,模擬Sycamore 最大任務需要15.9 天,而模擬祖沖之最大任務需要8.2 年.取決于使用的經典計算算法,祖沖之量子計算機實現的最大規模采樣任務對應的經典計算資源大概是Sycamore 實現的最大規模采樣任務對應的經典計算資源消耗2—3 個數量級.

2021 年9 月,潘建偉團隊又在祖沖之2.0 的基礎上升級到了祖沖之2.1.祖沖之2.1 相對于祖沖之2.0 的主要提升是將平均讀出精度從95.48%提升到了97.74%,因此可以在祖沖之2.1 上實現更大規模的、量子比特數為60、線路深度為24 層的隨機量子線路.這一采樣任務在經典計算機上實現的復雜度比Sycamore 實現的最難的采樣任務高6 個數量級,比祖沖之2.0 上實現的最難的采樣任務高3 個數量級[18].

量子計算機和經典算法都在發展,要從實驗上驗證量子優越性不是一個一蹴而就的事情,需要不斷地提高量子計算機的規模和精確度,得益于量子計算機計算空間上隨量子比特數的指數增長,經典計算機很難模擬更大規模的量子線路.

3.2 玻色采樣的實驗進展

無論是理想玻色采樣還是高斯玻色采樣,其裝置都主要由3 部分構成:光子源、干涉儀以及最終的光子探測裝置,而不同的玻色采樣在實驗裝置上的區別僅體現為光子源不同.潘建偉團隊[53]在理想玻色采樣、容許損耗的玻色采樣、高斯玻色采樣方面均完成了有代表性的實驗工作,下面以他們的方案為例進行介紹.

圖7 為理想玻色采樣的實現方案,其光子源使用了一個很高質量的InAs/GaAs 量子點單光子源,可以76 MHz 的頻率穩定產生單光子.量子點可以看作是微納加工制備的一個電子二能級體系,利用其和諧振微腔的耦合,光子的自發輻射得到增強,最終可以實現由外加的脈沖激光光場將體系激發到高能級,確定性地輻射出單光子,故也稱作on-demand 單光子源.

圖7 九章GBS 實驗示意圖[53]Fig.7.Illustration of the Jiuzhang GBS experiment[53].

這些光子通過波導、反射鏡與分束器構成的網絡,其中的Pockels Cell 在外加電場的作用下可以受控地使光子偏振方向發生旋轉,而分束器將不同偏振的光子分離到不同的路徑上,如此實現了將單個光子源發出的全同光子分為20 個一組,每組同時輸入一個m=60 的干涉儀中,干涉儀等價于一個非常緊湊的由反射鏡和分束器組成的網絡,輸出端接入60 個獨立的超導單光子探測器 (光子探測器為工作在超導態-正常態相變臨界點的超導體,利用相變點附近很小的電磁場變化可以帶來很大電阻改變的這一特性,實現對單光子事件的探測).事實上,該實驗中在輸出端探測到的最多光子數事件為14 光子事件,每小時能收集到約6 次這樣的采樣.于是,該裝置自然地能夠完成對較少光子數的理想玻色采樣與較多光子時的容許損耗采樣.

大規模高斯玻色采樣的實驗實現,即“九章”實驗裝置,其干涉儀和探測器部分與前述理想玻色采樣裝置一致,而光子源部分,“九章”采用泵浦激光作用于25 塊非線性晶體PPKTP,生成25 個雙模壓縮態,等效于50 個單模壓縮態,輸入進m=100的干涉儀中,輸出端可以測量到的事件平均包含47 個光子,至多記錄到76 個光子的符合計數.

4 經典模擬進展

盡管量子優越性問題是經典計算難的,但由于目前量子設備的規模和誤差等的約束,經典模擬仍然是非常有必要的一個方向.一方面,經典計算機可以給出一個量子設備暫時不能達到的閾值,另一方面,經典計算機的模擬也可以用來驗證量子設備的可靠性.

4.1 隨機線路的經典模擬

Google 展示量子優越性的實驗是在53 可用量子比特的量子計算機上進行的最大規模為53 量子比特、20 層深度的隨機量子線路采樣,在200 s內可進行一百萬次采樣,采樣分布的保真度達到了0.2%,他們估計這一任務在目前最先進的超級計算機Summit 上需要10000 年才能完成[7].但這一估算是基于Google 團隊提出的算法,有沒有更好的經典算法能夠把模擬的時間減少到可實現的范圍內,對量子優越性成不成立提出了挑戰.同時,高效的經典算法本身也可以用于量子模擬,加速量子模擬器.

模擬量子電路主要有兩種方法.第一種方法存放整個量子態|ψ〉并且進行演化,這種方法被稱為Schr?dinger 方法[7],這種方法的優點是計算復雜度和電路深度d是線性關系,所以對比特數很少的電路非常有效,但是它的空間復雜度隨著量子比特數是呈指數增長的,對量子比特數多的電路,內存會成為一個瓶頸.目前為止,用這種方法在超算上實現的最大量子比特數電路的模擬是49 個量子比特[22].Iboldsymbol 提出了一種利用硬盤來進行存儲的基于張量網絡方法的方案,以模擬49 量子比特27 層深度電路的全振幅,以及56 量子比特深度為22 層的電路的部分振幅[19].為解決對內存需求過大的問題,Google 使用了Schr?dinger-Feynman方法,這個方法把電路切成兩塊,用費曼路徑積分把兩塊連起來,每一塊分別用Schr?dinger 方法進行計算,但是這樣勢必會增加算法的時間復雜度,正是基于這個方法才給出了在Summit 上需要10000 年時間的估計.

第二種方法基于張量網絡,只計算一個比特串或者一小部分比特串的振幅,量子電路可以被表示為張量網絡,通過張量網絡的縮并來計算一個特定比特串的振幅.可以通過張量網絡對應線圖的最優樹分解來找到張量網絡的最佳縮并順序,一般而言,找到圖的最佳樹分解是一個NP 難的問題,所以經常會用啟發式算法來找.雖然該方法得到的樹分解不是最佳,但也足夠好的樹分解.張量網絡方法的空間復雜度取決于縮并過程中出現的最大張量的階數,而最大張量的階數與量子電路對應的線圖的樹寬呈指數關系[66].當電路深度比較淺的時候,樹寬很小,即使對量子比特數目很大的電路,張量網絡方法也是非常有效的算法.但是張量網絡的計算復雜度經常與電路深度成指數關系.也可以通過圖分解算法等進行針對特定電路的高度優化來尋找張量網絡的好的縮并順序[67],這樣可以對Sycamore 量子線路模擬在Google 團隊的估計上加速10000 倍.基于這項工作,對縮并樹的主干進行優化之后,對于20 層電路深度的Sycamore 電路,阿里巴巴在和Summit 相當的超級計算機上實驗,可以在20 天內完成Google 團隊估計需要10000 年的算法[27].最近的一篇基于張量網絡的固定一部分比特串的工作,針對20 層深度的Sycamote 量子電路,5 天內在60 個GPU 的小集群上計算出兩百萬個比特串的振幅[28].

Li 等[22]在張量網絡的基礎上通過分析量子隨機線路的結構,開發CZ 門的對角性質,提出了一個新的技術—隱分解,對于 7×7 量子比特的隨機線路,該方法可以多分解額外的7 個CZ 門且不需要額外的空間,因此可以將Iboldsymbol 提出的通過張量網絡的slicing 技術求解全振幅經典模擬方法[19]中的被模擬電路的深度增加8 層(如圖1中的8 種排列模式).

4.2 玻色采樣的經典模擬

由于玻色采樣(及其衍生問題)求一個樣本的概率的最大代價在于求解其中的積和式(Hafinan函數、Torontonian 函數),因此對于玻色采樣的經典模擬工作主要包括計算一個振幅和進行一次采樣.由于玻色采樣的振幅可以顯式地寫出,因此求一個振幅相對隨機線路采樣而言較為容易.

對于采用超級計算機進行單個矩陣積和式/Hafnian/Torontonian 的計算,Wu 等[68]在天河二號上比較了兩個目前最高效的積和式算法—Ryser 算法和BB/FG 算法的運行效率,兩者計算單個積和式的復雜度均為O(n2n) .得到單個n=50矩陣積和式計算需要天河二號約 100 min 的結論.潘建偉團隊[69]通過在神威太湖之光超算上對矩陣的Torontonian 函數進行求解對高斯玻色采樣的經典計算耗時進行估算.

對于一個樣本的采樣問題,Clifford 和Clifford通過條件概率的思想大大降低了進行一次采樣的時間(和計算全振幅相比)[55].具體來講,由于玻色采樣其概率空間的特殊性,可以將一個n維的概率分布每一維單獨采樣,并計算下一維的條件概率,即將(7)式的概率分布轉化為“第k個光子在第rk個出口被探測到”,并將其概率分布表示為

如此,可以依次對n個光子出口位置進行采樣,通過化簡該條件概率函數,并對以上n個條件概率依次進行采樣,就可以實現經典計算機對玻色采樣問題的一次采樣的模擬.注意到這里

因此只需要求得所有的邊緣概率分布函數,就可以依次采樣得到r1,r2,···,rn.

對于玻色采樣,基于以上條件采樣的方法及對邊緣概率函數的優化方法,Clifford 和Clifford[55]證明了進行一次采樣的時間可以和計算常數個積和式的時間相等.同時,Neville 等[54]通過Metropolis獨立采樣方法,可以得到玻色采樣的一次近似采樣,他們可以在普通筆記本上實現30 個光子的采樣,在超算上實現50 個光子的近似采樣.但對于高斯玻色采樣和帶閾值的高斯玻色采樣,目前還沒有結論證明其采樣復雜性可以降低到求解常數個Hafnian 函數或是Torontonian 函數.但目前較好的后兩者采樣算法[41,56,57,70]都是利用了第二種方法中條件概率的思想去降低求解的代價.

5 總結和討論

近幾年來,量子計算機的規模和精度都得到了極大的提升,目前世界上最先進的量子計算機已經達到了50—100 個量子比特[17,18,53],單個門的誤差也降低到了0.2%左右[7,49].無論是學術界還是工業界,對量子計算的熱情都急速增長.未來量子計算的發展,很大程度上依賴于量子計算機硬件性能的提升與量子算法在物理化學生物等領域的實際應用的探索.本文所梳理的對采樣問題的量子優越性的研究,旨在找出一些量子計算機相較于經典計算機具有計算能力優勢的問題.盡管當前的采樣實驗在一定范圍內可以被經典模擬,但隨著實驗上規模的逐漸增大和設備精度的不斷提升,經典模擬將變得越來越困難.采樣問題的量子優越性研究一方面驗證了可控量子系統相較于經典計算更強的操作能力,另一方面也為下一步解決經典困難問題提供了基礎.隨著經典計算機的性能提升與算法的發展,經典計算機的算力也在提升,所以如果希望量子計算機能夠永遠戰勝經典計算機,就必須制備出大型穩定的通用量子計算機,并且需要對錯誤具有一定的魯棒性.

另一方面,量子系統也在不斷增大,量子實驗結果的正確性驗證也越來難.潘建偉團隊實現的基于帶閾值的高斯玻色采樣實驗[53]和隨機線路采樣實驗[17]在近期內仍未找到可以有效模擬和驗證的經典模擬算法.如何有效驗證中等規模量子計算是目前的一個重要研究方向.

與此同時,找到第一個有足夠實際應用價值的超越經典計算機性能的問題,是整個量子計算領域的重中之重.由于量子計算機的性能隨著規模的增大而指數增長,以及量子計算機獨特的疊加、糾纏等特性,量子計算機和經典計算機的結合將成為早期應用中最有可能出現的方案.QPU 與CPU,GPU,TPU 等處理器的結合,形成高效的異構體系,并以云平臺提供算力,正在成為工業界積極探索的方向.

值得注意的是,近期Google 團隊在Sycamore量子計算機上進行了一系列應用探索.在優化問題中,利用量子近似優化算法,在23 個物理量子比特上演示了Sherrington—Kirkpatrick 模型和最大割問題的量子版本算法[71].量子化學方面,結合量子變分算法計算了氫鏈的結合能與二氮烯分子異構化反應的能量躍遷,計算中最多用到了12 個量子比特,其中6 個原子與8 個原子的氫鏈的計算在引入錯誤抑制方案后,達到了化學精度[72].另外,在量子模擬方面,用16 個量子比特模擬了一維Fermi-Hubbard 模型的時間演化,觀察到了自旋-電荷分離現象[73].然而遺憾的是,量子計算機上演示的以上實際應用問題并未真正體現出量子計算機相較于經典計算機的優勢.

在機器學習領域,近期也有一些體現量子優越性的量子機器學習方案被提出,比如Liu 等[74]巧妙地設計了一個基于離散對數問題的學習問題,并證明了其量子優越性.具體來說,該量子機器學習算法的量子分類器是一個傳統的支持向量機,通過使用容錯量子計算機來估計核函數.他們同時證明了在假設離散對數問題是經典困難的情況下,沒有經典的多項式時間的學習算法可以比隨機選取更好.但由于求解離散對數問題的量子算法需要大規模的通用量子計算機,也許該優越性問題需要一定時間才能真實體現其優勢.對于學習量子態的線性性質問題,Huang 等[75]論述了可以通過量子計算機的糾纏能力,將多個量子態的拷貝通過量子電路糾纏起來,從而實現對直接通過經典測量的經典學習算法進行指數加速.因為該實驗需要的量子資源較少,因此有望在不久的將來在中等規模帶噪音等量子(noisy intermediate-scale quantum,NISQ)機器上進行展現.

本文對于量子優越性問題的回顧和探索在這里將告一段落,但科學界對量子優越性的探索遠不止以上這些問題.隨著工業界和高校在量子設備規模上的里程碑進展,未來能夠在量子設備上展現出優越性的問題將會越來越多.