光電流驅動下非線性神經元電路的放電模式控制*

謝盈 朱志剛 張曉鋒 任國棟

(蘭州理工大學物理系,蘭州 730050)

放電模態是可以識別生物神經元的電活動,即細胞內和細胞外的離子被泵送并在細胞內交換的過程.通過適當的物理刺激,人工神經元電路可以被設計以重現類似生物神經元的放電模式.光電管中產生的光電流可以作為信號源,對神經元電路進行刺激.但由于不同支路上的通道電流對功能神經元動力學的控制程度不同,所以光電管接入不同的支路,將會使神經元電路的放電模式產生很大差異.本文所采用的非線性神經元是由一個電容器、感應線圈、非線性電阻、兩個理想電阻和一個周期電壓源組成的FHN (FitzHugh-Nagumo neuron)電路.在此基礎上,將光電管引入不同的支路來改變通道電流,以研究光電流的生物物理作用.當光電管連接到電容上,光電管被激活從而改變通道電流時,細胞膜電位可以直接改變,并切換激發模式.當光電管串聯連接到感應線圈時,通過感應線圈的感應電流被調節以平衡外部刺激.這些結果表明,在本文構建的兩類光敏神經元模型中,相比光電流驅動電感支路,光電流驅動電容器支路可以更有效地調節膜電位,大大提高感光靈敏度.

1 引言

神經系統是龐大的復雜網絡,由神經元(即神經細胞)和神經膠質細胞組成.神經系統可以將各類信息進行編碼處理[1],而主要的信息整合和傳遞是由神經細胞完成的.生物神經系統中神經元的放電活動是通過離子在細胞膜間泵送和交換實現的,通過數學模型,可以研究其復雜的非線性動力學行為[2-5].當神經元受到一定刺激會產生沿細胞膜表面傳導的膜電位[6,7],即動作電位,它是神經元興奮或活動的標志.神經元的主要功能是在動作電位的刺激下,由鈣離子觸發細胞分泌神經遞質,并將神經沖動傳遞給其他神經元.而神經系統中,神經元之間信息傳遞的主要方式是突觸傳遞,包括神經遞質釋放、擴散等過程.在一些中間神經元中存在一種特定的突觸,即自突觸[8].自突觸可以改變神經元的電活動以及神經網絡的集體行為[9-12],反映神經系統的復雜時空動力學.

神經元或神經網絡電活動和受到一系列因素的影響,如外界刺激(光照、溫度等)、外界噪聲等外部因素,以及離子通道噪聲、熱噪聲等內部因素[13].事實上,常見的神經元模型主要考慮離子通道電流對細胞膜電位的影響.當考慮不同的物理刺激對通道電流的影響時,神經元模型可以被構造成為人工智能處理單元,用來感知和捕獲外部刺激來觸發適當的電活動,甚至可以展現出明顯的自適應能力[14].但直接對生物神經元放電活動的研究是困難的,而神經元電路以其簡便易搭建等優點為研究神經元的動力學行為提供了有效的途徑.在過去的幾十年中,不同的非線性神經元電路被設計用來模擬和研究神經動力學[15-17].

神經元電路的興奮性可以通過其輸出電壓體現.通過調整非線性電路中元件的參數,可以使神經元電路的輸出電壓呈現出與神經元的膜電位類似的靜息態、尖峰放電態、簇放電態,甚至是混沌放電態.當非線性電路[18-25]被激活時,用電容或電感耦合兩個非線性電路,連續的能量流在感應線圈和電容器中傳播和交換[26].能量的釋放和儲存在很大程度上取決于物理變量和電子元件,非線性電路的每個分支將共享和貢獻能量流,以便進一步交換.Wang 等[19]基于一種電阻電容電感分流的約瑟夫森結模型,用來論證了自適應控制器能耗與目標信號之間的關系,結果表明,利用追蹤控制方案來驅動混沌系統達到預定目標信號是可行的.文獻[25]以電磁感應效應為研究對象,利用FPGA設計了1 個數字神經元電路,該電路具有自動轉換連接的動態響應和生物學功能.另一方面,可靠的神經元模型[27-30]對于估計神經活動中的動力學特性和預測放電模式轉換具有重要意義.文獻[31]分別采用電突觸和化學突觸對基于憶阻器的Hindmarsh-Rose 神經元模型進行耦合,并分析了神經元的同步動力學特性.Wang 等[32]研究了非全同的神經元電路耦合模型動力學,數值結果表明通過調節耦合強度可以引起豐富的分岔行為.

事實上,在神經元電路中產生類似生物神經元電活動需要考慮一些現實因素,如電磁輻射[33,34]等.從物理角度來說,可以用等效的非線性振蕩器來描述一些復雜的神經網絡系統[9,35,36],如感溫觸覺神經系統、感光視覺神經系統等,來構造功能神經元.當神經元處于光照條件時,需要考慮光照對神經元放電活動的影響.實驗表明,光學參數振蕩器可以產生簇放電行為[37,38].Zhang 等[39]設計的一種約瑟夫森結耦合的功能性神經元系統,可以實現對外界磁場變化的感知.Xu 等[40]用熱敏電阻控制神經回路的分支電流或電流源,從而使神經元對溫度變得敏感,同時,該文獻還對比了熱敏電阻在不同支路對通道電流的影響,從而為設計感溫傳感器提供了理論依據.文獻[41]提出了一種新的模型,使突觸通過光纖通信通道耦合神經振蕩器,模擬腦神經元之間脈沖信號的突觸傳遞,發現接收振蕩器受到光電二極管的影響,光纖通信通道可以保證不同頻率比的同步.

在以前的大部分工作中,基本是把非線性元件固定在某個支路上分析某種非線性混沌電路的動力學特性.Liu 等[42]設計了一種簡單的光電管耦合神經電路,結果表明光電池可以與產生連續電壓源的神經電路耦合并捕獲外部光信號.該電路在人工眼設計方面具有潛在的應用前景.Guo 等[43]研究了憶阻器耦合的兩個光敏神經電路,并利用物理變量和參數的標度變換研究了耦合動力系統的同步穩定性,通過調節耦合通道得到相位同步和完全同步.基于一類光電神經元[42]相關研究結果的啟發,本文研究了光電管/信號源在神經元電路的不同位置處對神經元電路放電活動的影響,分別采用分岔分析[44-46]、相軌圖、李雅普諾夫指數等數值模擬方法分析了電路分岔參數對神經元模態轉化動力學行為的影響.

2 模型與方法

2.1 系統(1)—FHN 神經元電路

首先考慮以余弦電壓源為外界激勵源的簡單FHN 神經元電路模型,電路如圖1 所示.

圖1 余弦電壓源驅動的簡單FHN 電路的示意圖,其中NR 為非線性電阻,C 為電容,L 為感應線圈,R 和RS 為線性電阻(分壓電阻),E 為恒壓源,VS 為余弦電壓源.Fig.1.Schematic diagram for the FHN neural circuit.NR is a nonlinear resistor,C is capacitor,L represents induction coil,R and RS are linear resistors,E is a constant voltage source,and VS is the external voltage source.

在此基礎上,在電路中引入光電管,并研究光電管對神經元電路的物理特性影響(參見2.2 節、2.3 節).非線性電阻NR的電壓和電流之間的關系式為

其中,ρ,V0是電阻的歸一化參數;V是非線性電阻的電壓.

根據基爾霍夫定律及電路各元件的伏安關系得圖1 所示的電路方程:

為了使電路方程具有普適性和一般性,對 (2) 式采用以下的無量綱變換:

無量綱變換后的動力學方程(4)可以表達光敏神經元的動力學

其中,變量x表示膜電位,y表示恢復變量對應的慢電流.將外部激勵源選擇為

2.2 系統(2)—電容C 串聯光電管的FHN神經元電路

當將光電管串聯在電容C所在支路時,神經元電路圖如圖2 所示.

圖2 將光電管和電容串聯的FHN 電路原理示意圖,其中K 表示光電管中的陰極,A 表示光電管中的陽極Fig.2.Schematic diagram for the FHN neural circuit while phototube couples with capacitor.K denotes cathode and A represents anode in the phototube.

光管的光電流取決于外部照明和陰極的材料性能,當外部照明強度達到一定閾值時,光電流達到飽和值,如圖3 所示.

圖3 光電管電壓與光電流關系圖Fig.3.Plot of the relationship between voltage and photocurrent.

光電管的光電流和電壓的關系式為[47]

其中IH是光電管的最大電流,Vg是光電管的輸出電壓,Va是與光電管相關的反向截止電壓.事實上真正驅動電路系統的是光照強度i,其大小直接體現在飽和電流IH上.設飽和電流隨時間變化IH=IH(t),為了處理方便,假設飽和電流的變化導致偏置電壓隨時間的變化為簡單的余弦函數關系,Vg=V0B2cosω′t.通過計算微分方程數值解得到電容兩端的電壓VC隨時間的變化(dVC/dt)后可以利用(6)式反推飽和電壓IH(與光照強度ig一一對應)真實的時間序列ig=iC=CdVC/dt.

其中,V=VC+Vg是非線性電阻NR兩端的電壓,VC是電容器的輸出電壓,RS是線性分壓電阻,則對應圖2 的電路方程表達為

為了使電路方程具有普適性和一般性,對方程采用以下的無量綱變換:

無量綱變換后的動力學方程為

其中外部激勵源uS選擇同(5)式,且ug=B2cosωt.需要說明的是,在本文中,之所以選擇外部激勵源的頻率與光電管信號頻率相同,主要基于以下3 點考慮:1)為了簡單起見,神經元電路在相同頻率下驅動可以突出輸入信號強度的影響.2)避免出現不必要的準周期輸出信號.多頻信號驅動的特征之一是準周期的出現,即輸出信號的頻譜中具有多個基頻,這徒然增加了信號的模式識別復雜度.3)從實驗角度可以實現對光電信號的濾波.這也是以上兩點說明的基礎.當采用外部激勵頻率作為濾波的窗口頻率時,可以將光電管的光電信號調整為具有較窄頻譜的單色.

2.3 系統(3)—電感L 串聯光電管的FHN神經元電路

當光電管串聯在電感線圈L所在支路時,其電路圖如圖4 所示.

根據基爾霍夫定律及電路各元件的伏安關系得到電路圖4 的電路方程如下:

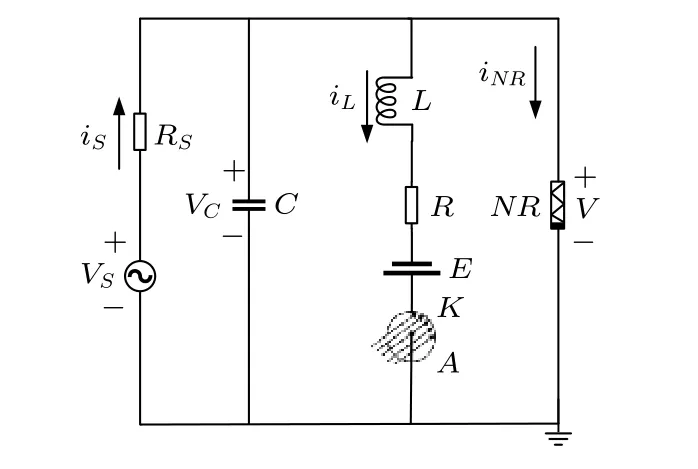
圖4 將光電管和恒壓源串聯的FHN 電路原理示意圖Fig.4.Schematic diagram for the FHN neural circuit while phototube couples with induction coil.

對方程(11)采用相似的無量綱變換,得到的光敏神經元模型為

其中,外部激勵源和光電管輸出為uS=B1cosωτ,且ug=B2cosωτ.

3 數值結果與討論

在數值模擬中,采用四階龍格-庫塔算法解微分方程,時間積分步長選取為h=0.01,變量初始值為(x,y)=(0.2,0.1),FNH 神經元的歸一化參數選取為a=0.7,b=0.8,c=0.1.

3.1 系統(1)—FHN 神經元電路

首先,為了討論神經元電路系統(4)(無光電管驅動)的動力學特性,確定各種放電模式,進行相關的數值計算,并繪制系統的動力學隨參數B1,ω,ξ變化的分岔圖和李雅普諾夫指數圖,分別如圖5 和圖6 所示.

由圖5 可知,當FHN 神經元電路的參數a,b,c固定時,改變外界驅動參數B1,ω,ξ,系統可以呈現出不同的放電模式,特別是可以出現混沌放電態.系統出現混沌態的參數區域分別為B1∈[0.81,1.05],ω∈[0.36,0.42],ξ∈[0.17,0.2].

圖5 和圖6 的結果表明:分岔圖和李雅普諾夫指數譜所表現的動力學行為完全一致,當選取適當的外部刺激,最大李雅普諾夫指數為正,可以誘發混沌行為.為了更直觀地了解不同參數下的放電模式及其動力學性質,畫出各種放電狀態下的時間序列圖(圖7).

圖5 不同分岔參數(B1,ω,ξ)下的分岔圖 (a) ω=0.4,ξ=0.175;(b) B1=0.8,ξ=0.175;(c) B1=0.8,ω=0.4,其中參數a=0.7,b=0.8,c=0.1,初始值為(x,y)=(0.2,0.1)Fig.5.Bifurcation diagram calculated by changing the bifurcation parameters (B,ω,ξ) at a=0.7,b=0.8,c=0.1,initial parameters (x,y)=(0.2,0.1):(a) ω=0.4,ξ=0.175;(b) B1=0.8,ξ=0.175;(c) B1=0.8,ω=0.4.

圖6 不同分岔參數(B1,ω,ξ)下的李雅普諾夫指數圖 (a) ω=0.4,ξ=0.175;(b) B1=0.8,ξ=0.175;(c) B1=0.8,ω=0.4,其中參數a=0.7,b=0.8,c=0.1,初始值為(x,y)=(0.2,0.1)Fig.6.Distribution for the Lyapunov exponent spectrum calculated by changing the bifurcation parameters (B1,ω,ξ) at a=0.7,b=0.8,c=0.1,initial parameters (x,y)=(0.2,0.1):(a) ω=0.4,ξ=0.175;(b) B1=0.8,ξ=0.175;(c) B1=0.8,ω=0.4.

圖7 不同分岔參數下的時間序列圖,其中固定參數ω=0.4,ξ=0.175,(a1) B1=0.001,(a2) B1=0.5,(a3) B1=0.9,(a4) B1=1.1;固定參數B1=0.8,ξ=0.175 時,(b1) ω=0.11,(b2) ω=0.31,(b3) ω=0.4,(b4) ω=0.5;固定參數B1=0.8,ω=0.4 時,(c1) ξ=0.15,(c2) ξ=0.175,(c3) ξ=0.21,(c4) ξ=0.45.參數a=0.7,b=0.8,c=0.1,初始值為(x,y)=(0.2,0.1)Fig.7.Firing patterns generated by applying different bifurcation parameters at a=0.7,b=0.8,c=0.1,initial parameters (x,y)=(0.2,0.1):(a1) B1=0.001,(a2) B1=0.5,(a3) B1=0.9,(a4) B1=1.1 with fixed parameters ω=0.4,ξ=0.175;(b1) ω=0.11,(b2) ω=0.31,(b3) ω=0.4,(b4) ω=0.5 with fixed parameters B1=0.8,ξ=0.175;(c1) ξ=0.15,(c2) ξ=0.175,(c3) ξ=0.21,(c4) ξ=0.45 with fixed parameters B1=0.8,ω=0.4.

當固定其他參數(ω=0.4,ξ=0.175),隨著參數B1的增大,系統經過靜息放電、單周期放電過渡到混沌放電狀態,而后轉變為尖峰放電狀態(圖7(a1)—(a4)).若固定參數B1=0.8,ξ=0.175,只改變參數ω,系統經過單周期放電、尖峰放電過渡到混沌放電狀態,而后轉為單周期放電(圖7(b1)—(b4)).固定參數B1=0.8,ω=0.4,只改變參數ξ,系統首先從單周期放電過渡到混沌放電狀態,而后繼續呈現出不同的尖峰,周期放電狀態(圖7(c1)—(c4)).因此,系統在不同的參數調制下有不同的通向混沌態的道路.

圖5—7 的結果集中反映出該神經元電路的膜電壓可以在不同的外界刺激條件(振幅和頻率)下呈現出不同的放電模式,即靜息放電態、尖峰放電態以及混沌放電態.

3.2 系統(2)—電容C 串聯光電管的FHN神經元電路

對于動力系統(2)(第一類光敏神經元模型(10)),在電容器所在支路接入光電管.在神經元電路中引入光電管,可以模擬感光神經元,研究光照刺激對神經元動力學特性的影響.特別地,由于光電管的引入,神經元電路擁有了更多可調參數.為簡單起見,把光電管輸出刺激視為周期性電壓信號,無量綱后即為ug=B2cosωτ,ω為外界刺激電壓的角頻率.為了確定光電管對神經元電路的影響,繪制該模型在改變參數B2情況下的分岔圖,如圖8 所示,其中FHN 神經元的內稟參數選為與系統(1)中的參數相同的典型值,a=0.7,b=0.8,c=0.1,B1=0.8,B2=0.2,ξ=0.175.

從圖8 可以看出,在其他參數確定的情況下,當外界刺激的角頻率ω小于1,例如ω=0.001,0.01 或0.1 時,在振幅范圍內B2∈(0,2],混沌被抑制.當角頻率ω增大到一定值后,系統可以呈現出混沌放電狀態,例如當ω=0.4 時,在區間B2∈(0,0.3]中系統為混沌放電狀態.由于光電管的引入,神經元電路的可調參數空間維度增加.為了說明維度增加的效應對動力學分岔的影響,計算不同的參數組合下的分岔圖(圖9).

圖8 不同分岔參數ω 下,關于B2 的分岔圖 (a) ω=0.001;(b) ω=0.01;(c) ω=0.1;(d) ω=0.4;其中參數a=0.7,b=0.8,c=0.1,B1=0.8,ξ=0.175,初始值為(x,y)=(0.2,0.1)Fig.8.Bifurcation diagram of B2 calculated by changing the bifurcation parameter ω at a=0.7,b=0.8,c=0.1,B1=0.8,ξ=0.175,initial parameters (x,y)=(0.2,0.1):(a) ω=0.001;(b) ω=0.01;(c) ω=0.1;(d) ω=0.4.

圖9 結果表明,通過分別改變參數B1,ω,ξ,B2,系統出現混沌態的參數區域分別為B1∈[0.67,0.94],ω∈[0.38,0.5],ξ∈[0.15,0.19],B2∈(0,0.3].與系統1 無光電管耦合情況(圖5)相比較,當B2=0.2,參數ω,ξ的混沌區域并沒有太大變化,但是對于B1,出現混沌的區域明顯縮小,從B1∈[0.81,1.05]縮減至B1∈[0.67,0.94].此外,為了驗證混沌態的實現,還計算了對應參數下的李雅普諾夫指數圖.如圖10 所示,其結果和分岔圖結果一致.

圖9 不同分岔參數(B1,ω,ξ,B2)下的分岔圖 (a) B2=0.2,ξ=0.175,ω=0.4;(b) B2=0.2,B1=0.8,ξ=0.175;(c) B2=0.2,B1=0.8,ω=0.4;(d) B1=0.8,ξ= 0.175,ω=0.4;其中參數 a=0.7,b=0.8,c=0.1,初始值為 (x,y)=(0.2,0.1)Fig.9.Bifurcation diagram calculated by changing the bifurcation parameters (B1,ω,ξ,B2) at a=0.7,b=0.8,c=0.1,initial parameters (x,y)=(0.2,0.1):(a) B2=0.2,ξ=0.175,ω=0.4;(b) B2=0.2,B1=0.8,ξ=0.175;(c) B2=0.2,B1=0.8,ω=0.4;(d) B1=0.8,ξ=0.175,ω=0.4.

對比圖10(a)—(c)與圖6(a)—(c)的結果可以發現,當固定參數B2=0.2 時,系統出現周期態的參數區域沒有很大差異.而圖10(d)結果表明,在改變參數B2的情形下,混沌態出現在較大的B1所在區域內.并且,當B2∈[0.3,2.0]時,系統可以有效誘發不同的放電狀態.

圖10 不同分岔參數(B1,ω,ξ,B2)下的李雅普諾夫指數圖 (a) B2=0.2,ξ=0.175,ω=0.4;(b) B2=0.2,B1=0.8,ξ=0.175;(c) B2=0.2,B1=0.8,ω=0.4;(d) B1=0.8,ξ=0.175,ω=0.4;其中參數 a=0.7,b=0.8,c=0.1,初始值為(x,y)=(0.2,0.1)Fig.10.Distribution for the Lyapunov exponent spectrum calculated by changing the bifurcation parameters (B1,ω,ξ,B2) at a=0.7,b=0.8,c=0.1,initial parameters (x,y)=(0.2,0.1):(a) B2=0.2,ξ=0.175,ω=0.4;(b) B2=0.2,B1=0.8,ξ=0.175;(c) B2=0.2,B1=0.8,ω=0.4;(d) B1=0.8,ξ=0.175,ω=0.4.

為了更直觀地描述光電模型(10)在不同參數下的動力學特征,繪制了系統在不同參數設置下的時間序列圖(圖11).由于光電管串聯在電容所在支路上會使得新神經元系統具有更多的分岔參數,與無光電管耦合的神經元電路相比,存在新的通往混沌的路徑和方式,即參數B2.如圖11(a1)—(a4)所示,固定參數ω=0.4,ξ=0.175,B2=0.2,改變參數B1,系統經過靜息放電過渡到混沌放電狀態,而后繼續呈現出尖峰放電.如圖11(b1)—(b4)所示,固定參數B1=0.8,ξ=0.175,B2=0.2,改變參數ω,系統經過靜息放電、多周期放電、尖峰放電過渡到混沌放電狀態.如圖11(c1)—(c4) 所示,固定參數B1=0.8,ω=0.4,B2=0.2,改變參數ξ,系統經過靜息放電過渡到混沌放電狀態,而后繼續呈現出周期放電狀態.如圖11(d1)—(d4)所示,固定參數B1=0.8,ω=0.4,ξ=0.175,系統出現混沌放電狀態后改變參數B2取值,系統可以出現不同的周期放電狀態.另一方面,通過固定B2以外的其他參數,可以有效抑制混沌放電.

圖11 不同分岔參數下的時間序列圖,其中固定參數ω=0.4,ξ=0.175,B2=0.2 時,(a1) B1=0.1,(a2) B1=0.8,(a3) B1=1.2,(a4) B1=1.75;固定參數B1=0.8,ξ=0.175,B2=0.2 時,(b1) ω=0.001,(b2) ω=0.18,(b3) ω=0.25,(b4) ω=0.4;固定參數B1=0.8,ω=0.4,B2=0.2 時,(c1) ξ=0.005,(c2) ξ=0.175,(c3) ξ=0.5,(c4) ξ=1.5;固 定 參 數B1=0.8,ω=0.4,ξ=0.175 時,(d1) B2=0.2,(d2) B2=0.28,(d3) B2=1.0,(d4) B2=1.6.其中參數a=0.7,b=0.8,c=0.1,初始值為(x,y)=(0.2,0.1)Fig.11.Firing patterns generated by applying different bifurcation parameters at a=0.7,b=0.8,c=0.1,initial parameters (x,y)=(0.2,0.1):(a1) B1=0.1,(a2) B1=0.8,(a3) B1=1.2,(a4) B1=1.75 with fixed parameters ω=0.4,ξ=0.175,B2=0.2;(b1) ω=0.001,(b2) ω=0.18,(b3) ω=0.25,(b4) ω=0.4 with fixed parameters B1=0.8,ξ=0.175,B2=0.2;(c1) ξ=0.005,(c2) ξ=0.175,(c3) ξ=0.5,(c4) ξ=1.5 with fixed parameters B1=0.8,ω=0.4,B2=0.2;(d1) B2=0.2,(d2) B2=0.28,(d3) B2=1.0,(d4) B2=1.6 with fixed parameters B1=0.8,ω=0.4,ξ=0.175.

3.3 系統(3)—電感L 串聯光電管的FHN神經元電路

進一步討論光敏神經元模型(12)對應的神經元電路輸出特性,即光電管與電感線圈串聯.為了對比系統(3)的動力學行為與系統(1)和系統(2)的不同,選擇與模型(10)同樣的參數設置,a=0.7,b=0.8,c=0.1,ξ=0.175,B1=0.8,B2=0.2,ω=0.4.圖12 為系統(3)在相應參數下的分岔圖.

圖12 的結果表明,在保持與模型(10)相同的分岔參數條件下,當光電管置于電感所在支路時,同樣可誘發不同的放電狀態.一方面,比較圖9(b)、圖9(c)與圖12(b)、圖12(c),發現兩種光敏神經元模型和電路出現混沌的區域和各分岔點的位置沒有發生太大變化,且兩類系統分岔圖的結構也是相似的.然而,對比圖9(a)—(d)和圖13(a)—(d),發現當固定其他參數而改變振幅B1,B2時,兩類神經元的分岔圖具有明顯的不同.首先,當光電管耦合到電感線圈所在支路上時,出現混沌的參數區域變大,為B2∈(0,0.39],而B1的范圍確縮減至B1∈[0.67,0.94].其次,兩類系統通往混沌的路徑也不同,光電管與電感耦合時,系統典型非混沌態為多周期;而當光電管與電容器耦合時,系統隨著B1的減小,從單周期不斷通過倍周期分岔通往混沌態.

圖12 不同分岔參數(B1,ω,ξ,B2)下的分岔圖 (a) B2=0.2,ξ=0.175,ω=0.4;(b) B2=0.2,B1=0.8,ξ=0.175;(c) B2=0.2,B1=0.8,ω=0.4;(d) B1=0.8,ξ=0.175,ω=0.4;其中參數a=0.7,b=0.8,c=0.1,初始值為(x,y)=(0.2,0.1)Fig.12.Bifurcation diagram calculated by changing the bifurcation parameters (B1,ω,ξ,B2) at a=0.7,b=0.8,c=0.1,initial parameters (x,y)=(0.2,0.1):(a) B2=0.2,ξ=0.175,ω=0.4;(b) B2=0.2,B1=0.8,ξ=0.175;(c) B2=0.2,B1=0.8,ω=0.4;(d) B1=0.8,ξ=0.175,ω=0.4.

在圖13 中繪制了相應參數下的李雅普諾夫指數圖,李指數的正負切換與分岔圖的動力學行為完全一致.比較圖10(a)—(c)和圖13(a)—(c)之間可以看出,兩類系統李亞普諾夫指數譜的結構是相似的,而圖10(d)和圖13(d)的Lyapunov 指數譜的結構完全不同,從而進一步驗證了上述現象.

圖13 不同分岔參數(B1,ω,ξ,B2)下的李雅普諾夫指數圖 (a) B2=0.2,ξ=0.175,ω=0.4;(b) B2=0.2,B1=0.8,ξ=0.175;(c) B2=0.2,B1=0.8,ω=0.4;(d) B1=0.8,ξ=0.175,ω=0.4;其中參數a=0.7,b=0.8,c=0.1,初始值為 (x,y)=(0.2,0.1)Fig.13.Lyapunov exponent spectrum calculated by changing the bifurcation parameters (B1,ω,ξ,B2) at a=0.7,b=0.8,c=0.1,initial parameters (x,y)=(0.2,0.1):(a) B2=0.2,ξ=0.175,ω=0.4;(b) B2=0.2,B1=0.8,ξ=0.175;(c) B2=0.2,B1=0.8,ω=0.4;(d) B1=0.8,ξ=0.175,ω=0.4.

此外,從非線性諧振子方面考慮,對方程(4),(10)和(12)作如下變換,即通過方程中的第1 個式子得到y關于x的表達式,然后代入第2 個式子中得到二次非線性方程,由此定義系統的有效幅值R.無光電管驅動的神經元電路對應的神經元(4)可以表達為

其對應的有效幅值定義為

為簡單起見定義z=x+ug,對應的光敏神經元(10)可以表達為

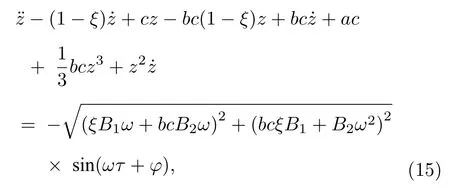
則其對應的有效幅值為

同樣地,第二類光敏神經元(12)動力學等效表達為

其對應的有效幅值可以表達為

3 類有效幅值的表達式表明,此3 類系統的動力學形式是等價的,系統的動力學行為與R,ω之間具有直接聯系.在相同的驅動頻率和其他固定參數下,它們之間的主要不同體現在有效幅值上,即有效幅值R1,2,3對不同參數具有不同的函數依賴關系.事實上,從非線性動力學方程分析,當光電管與電容器串聯時,只改變了系統的外在驅動;而當光電管耦合電感線圈時,方程(12)中兩個等式中都存在正弦信號,即系統除了有外在驅動,還有參數驅動效應的參與,而這個參數驅動也是周期性變化的.另一方面,從(14)式、(16)式、(18)式可以看出,R的改變會伴隨著頻率和幅值同時改變,且3 個系統與頻率、振幅的函數關系也不一樣.

以上結果表明,在同一參數設定下,3 種神經元模型都能夠誘發出不同的放電狀態(靜息、周期、混沌放電狀態),且有著不同的通向混沌放電的道路.相比無光電管耦合的情形,光敏神經元電路比一般的FHN 神經元電路具有更豐富的神經元放電現象和更多可調參數.一方面,對于這3 類神經元模型而言,出現混沌態的分岔區域有相似之處,即參數ω,ξ的分岔區間是相似的;另一方面,值得注意的是,當光電管與電容串聯時,若外界刺激的角頻ω小于1,例如ω=0.001,0.01 或0.1 時,在振幅范圍內(B2∈(0,2]),可以有效抑制混沌放電現象的出現.此外,在無光電管驅動的神經元中選擇同樣的參數時,第1 類光敏神經元(10)出現混沌放電狀態的參數(B2)區域為B2∈(0,0.3];不同于光電管串聯電感的是,當光電管在電容所在支路時,系統對光電管信號的幅值更為敏感;此外,兩種耦合方式都明顯縮減了出現混沌放電狀態下參數B1的區間.另外,通過計算和對比3 類連接方式所對應的二階非線性方程,發現在單個簡諧信號驅動下,3 類系統的非線性動力學方程可以統一成相同的形式,其區別在于等效驅動信號的有效幅值和頻率的不同.

4 結論

在被激活非線性電路中,能量的釋放和儲存在很大程度上取決于物理變量和電子元件屬性,連續的能量流在感應線圈和電容器中傳遞和交換,即非線性電路的每個分支將共享和貢獻能量流.本文構建并研究了兩類光敏神經元電路模型在光電流驅動下膜電位的模式轉換性質,從生物物理的角度模擬了不同感光神經元細胞對光信號的響應.基于簡單的FHN 神經元電路,在不同支路中接入光電管來驅動神經元電路系統,從而有效增強神經元電路的物理響應.由于通道電流依賴于光電管信號輸入與電路元件之間的相互作用,其效應體現在信號特征的改變會引起不同類神經元電路的動力學分岔結果不同,進而影響放電模式的輸出差異.特別地,周期性輸入信號的頻率和幅值決定了神經元電活動的模式轉換.

結果表明,適當的周期性刺激可以觀察到適當的神經元動力學響應,即神經元的興奮性受到外界光信號的調控,可以使FHN 神經元有效誘發神經元電路的不同放電模式.并且,在同一參數設定下,3 種神經元都能夠誘發不同的放電狀態,且可以沿著不同路徑產生混沌.相比無光電管耦合的情形,光敏神經元電路具有更好的可控性.實際上,當光電管與電容器串聯時,等同于光電管的輸出電壓直接作用于膜電位上;而光電管與電感串聯時,等同于作用在通道電流上,屬于間接作用.相比于第1類光敏神經元模型,第2 類光敏神經元在各參數下出現混沌的臨界點均向后移動,且其動力學對參數B2的變化更為敏感.另外,計算3 類神經元模型所對應的二階非線性方程,一定條件下3 類系統的非線性動力學方程可以統一成相同的形式,其區別僅在于等效驅動信號的有效幅值和頻率的不同.

總而言之,神經元電活動的模式選擇依賴于外界光信號刺激對不同電路元件的刺激方式.這些結果有助于進一步研究在光信號輸入情況下功能性神經元網絡的集體行為,并為光敏神經元在人工眼、人機交互等方面的應用提供了理論依據.

課題組姚昭博士對本論文的數值計算結果進行仔細驗證并修改筆誤,馬軍教授對修改稿的文字部分和結論給予的寶貴意見,作者在此表示真誠感謝.