無速度多追蹤的量化間歇控制

唐 茜，涂細凱，鄭笑雨，張冰冰

（1.湖北工業大學工業設計學院，湖北 武漢 430068；2.湖北工業大學機械工程學院，湖北 武漢 430068）

1 引言

過去二十幾年來，多智能體的分布式協同控制一直是各學科非常感興趣的話題，廣泛的應用于分布式一致性、編隊控制、包容控制和同步等。其中，一致性問題是分布式協同的關鍵問題[1-3]。一般來說，一致性問題的目標是設計合適控制算法，通過鄰居智能體之間的局部信息交換，使得所有智能體的狀態最終收斂到一致。

根據網絡領導者的數量，一致性可以分為：無領導一致性、一致性追蹤（Leader-Following）和多追蹤（Multi-Tracking）等。近些年來，多追蹤問題受到越來越多的注意。多追蹤問題中，一個多智能體網絡由多個群集組成，每個群集的所有跟隨者的狀態最終收斂于領導者的軌跡，同時，不同的群集之間收斂的軌跡不同[4-5]。注意到，代數圖理論一直是研究多智能體一致性問題[6-8]的有效方法。

值得注意的是相比于位置信息，智能體的速度信息更難測量。因此，研究速度不可測的二階多智能體系統的一致性問題是非常有必要的。前文提到大部分工作的前提是智能體之間信息的傳輸是連續的，然而，由于傳輸帶寬的限制，這種傳輸形式不太可靠。因此，對于研究二階多智能體系統的一致性問題來說，與連續數據相比，采樣數據是更實際的來源。

在實際應用中，由于傳輸信息的帶寬有限制，采樣數據需要提前量化。因此，使用量化數據研究多智能體的一致性問題更有現實意義。進一步，量化誤差對網絡一致性性能的影響也不能忽視。但是，針對具有量化數據的二階多智能體系統的一致性結論并不多。另一方面，在各種量化方法中，隨機量化器的量化間隔是平均的，并且其量化誤差的特性可以用于研究一致性問題。因此，針對二階多智能體系統的一致性問題，采用了隨機量化的方案進行研究。通信時滯的影響也應該要考慮，因其是降低網絡性能的另一個因素。

針對考慮通信時滯的二階多智能體系統，提出了一種量化的間歇控制規則用于解決系統的多追蹤問題。不同于上述文獻，僅僅使用了系統的采樣位移信息，且控制輸入是可變的。同時，引入了隨機量化的方案，在傳輸之前量化位移信息。基于代數圖論、隨機量化和穩定性理論，分析得到了被控系統實現多追蹤的一些充分必要條件。

符號定義：定義m階單位矩陣為I∈?m×m，m階零矩陣為0 ∈?m×m，并將I5∈?5N×5N簡化為I5。定義1ml∈?ml×1為所有元素是1的ml階列向量，Re(·)和Im(·)分別是復數的實部和虛部。AT和det(A)分別代表矩陣A的轉置和行列式。?為Kronecker運算，P{·}和E{·}分別代表量化和期望運算。

2 預備知識和多追蹤問題

2.1 預備知識

加權有向圖G={V，ε，A} 中節點集為V={1，2，…m}，邊集為ε?V×V，非對稱加權鄰接矩陣為A=[aij]∈?m×m。假如從節點j到節點i存在一個有向連接，則定義e(j，i)∈ε。當且僅當e(j，i)∈ε時aij＞0，假設沒有自回路，也就是說對所有i∈V，令aii=0。定義節點i∈V的鄰居節點集為Ni={j∈V，|(j，i)∈E}，節點i∈V的入度為。有向圖G的對角矩陣為D=，拉普拉斯矩陣定義為L=D-A。

定義1：（子網絡）定義網絡Gs={Vs，εs，As} 為 網 絡G={V，ε，A} 的子網絡，滿足Vs?V、Es?E和As?A。

2.2 問題描述

考慮具有m個節點的多智能體網絡G={V，ε，A}，其由n≥2個子網絡Gs={Vs，εs，As} (s=1，2，…，n)組成，每個子網絡包含ms個節點，并且滿足。同時，對任意s≠s′，Vs≠?，滿足。第sth個子網絡的節點標記為Vs=，且令m0=0。

基于文獻[9]中對隨機量化的定義：假設數據h∈[-R，R]量化后長度為l比特，那么，我們可以得到量化點r=2l個和量化區間δ=2R/2l，以下為量化數據的方式：

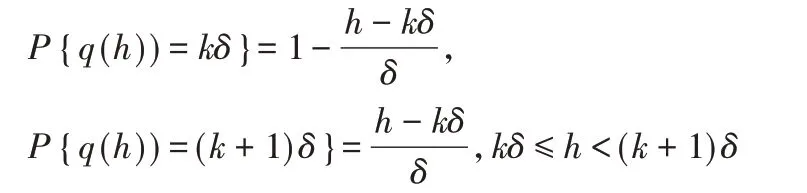
那么，對于此量化器我們可以得到一個很重要的特性：

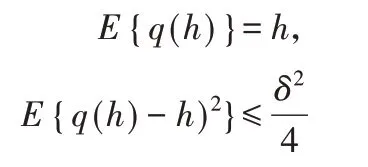
假設每個智能體具有如下二階動態特性：

其中，xi(t)∈?，νi(t)∈? 分別是智能體i(i=1，2，…，m)的位移和速度量。μi(t)為狀態反饋量。

第sth個子網絡期望的追蹤軌跡為：

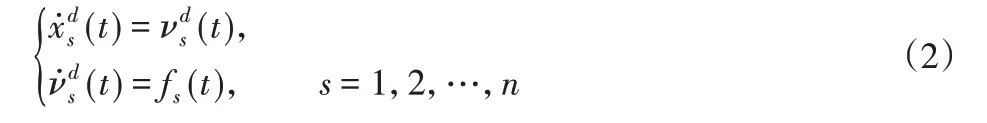
其中，fs≥0 ∈[0，+∞)在時間t內是分段連續的函數，(t)∈?，∈?表示第sth個子網絡期望的位移和速度量。僅研究了二階多智能體的勻速多追蹤問題，即fs=0。

二階多智能體系統（1）在期望軌跡為（2）下的多追蹤問題可以重新寫為：

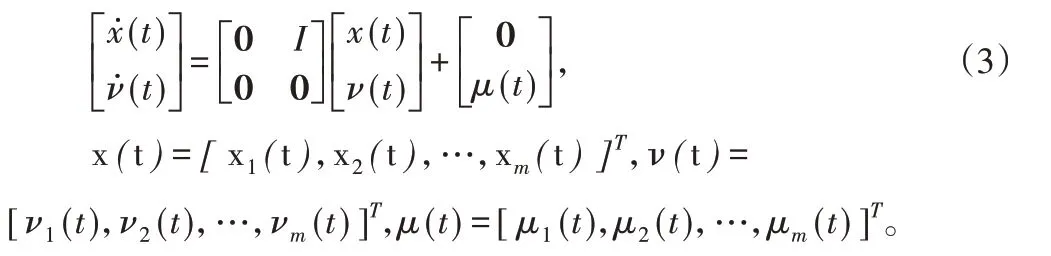
定義2：對任意初始狀態，二階多智能體系統（1）能夠實現多追蹤當且僅當

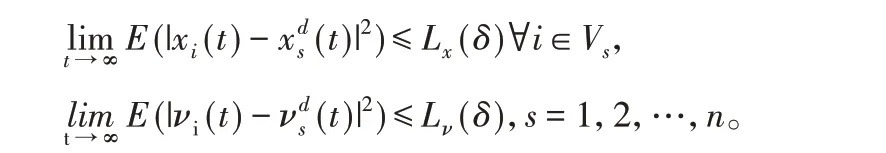
其中，Lx和Lν是關于δ的兩個單調遞增函數，且滿足：

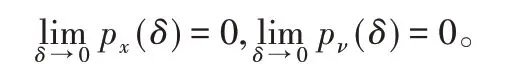
3 通信時滯下的量化間歇控制

在實際應用中，信息傳輸的過程中不可避免的存在時滯，這種情況對一致性控制協議的性能有很大的影響。假設多智能體系統通信時滯為τ，智能體之間只在采樣時刻進行通信，采樣時間序列為0 ≤t0＜t1＜…＜tk＜…，那么定義采樣區間為ξ=tk-tk-1。針對多追蹤問題提出了如下間歇控制方案：

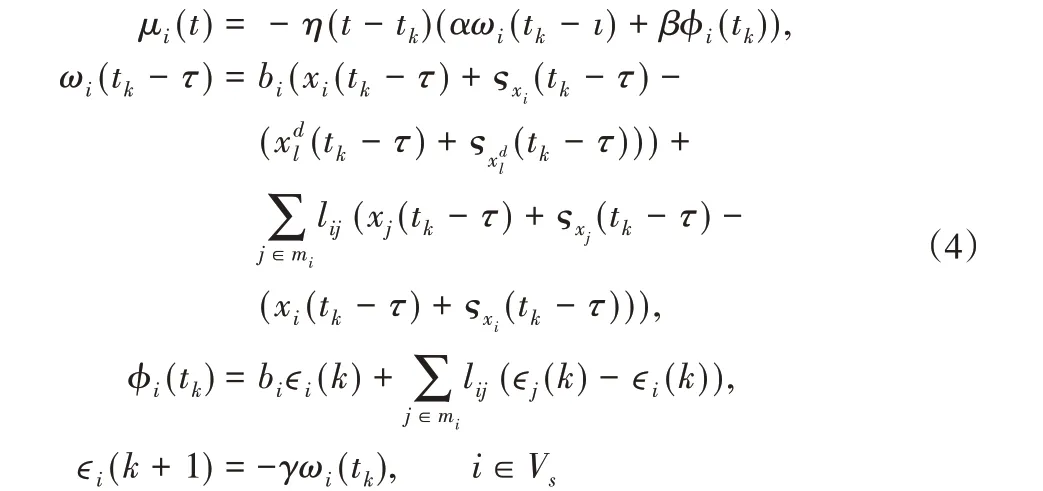
其中，控制參數α＞0，β＞0，γ＞0，tk＜t≤tk+1。?xi(tk)=q(xi)-xi為第ith個智能體的位移量化誤差為第sth個子網絡的期望位移量化誤差。η(t)為脈沖函數，表示如下：

其中，ε∈(0，ξ]為控制持續時間，函數(t)的選取可以依據不同的狀態，可以為矩形函數、三角函數、梯形函數和非線性函數。從量化方程我們可以得到位移量化誤差的如下性能：

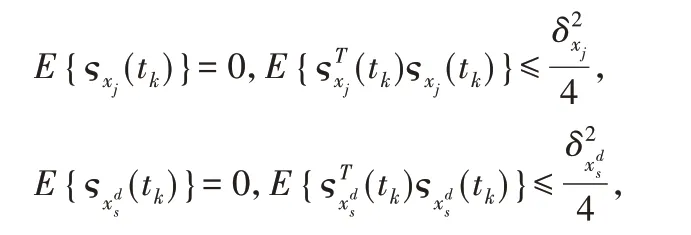
其中，δxj和δxds分別為智能體的位移和期望位移的量化誤差區間。

令

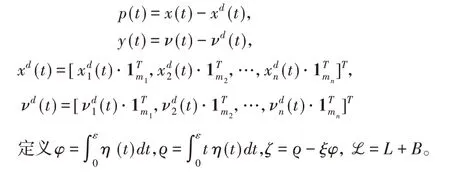
令H(tk)=[p(tk)T，y(tk)T，?(k)]T，多智能體系統（1）可以改寫為：

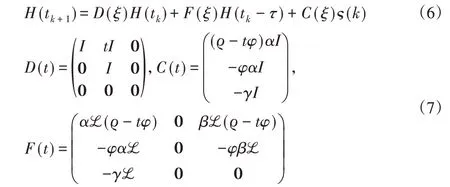
全文只考慮通信時滯滿足τ＜ξ-ε的情況，

令：

引理1：[10]基于控制協議（4），二階多智能體系統（1）可以實現多追蹤當且僅當ρ(A)＜1，其中ρ(·)為矩陣A的譜半徑。

證明：令

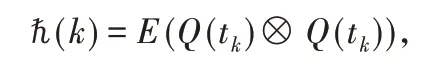
從式（8）可得，

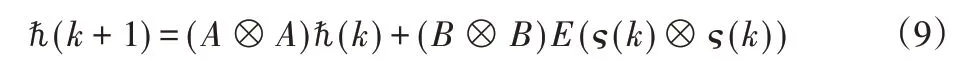
明顯可知，

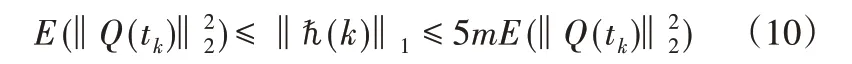
必要性：如果ρ(?)≥1，那么ρ(? ??)≥1，基于控制協議（4）的多智能體系統（1）一定是分散的，無法實現多追蹤。

充分性：如果ρ(?)＜1，那么ρ(? ??)＜1，一定存在一個足夠小的常數?＜1滿足‖? ??‖2=?＜1。那么

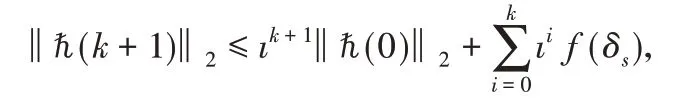
其中，f(δs)=。

由于?＜1，可得：

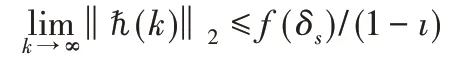
并且，

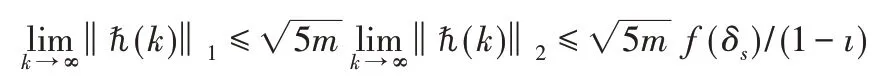
結合不等式（10），

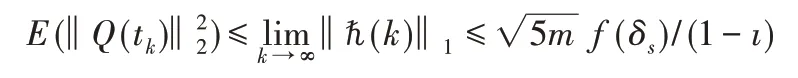
因此，存在正的常數a＞0和b＞0，使得

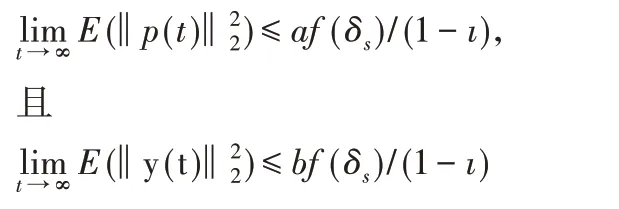
也就是說

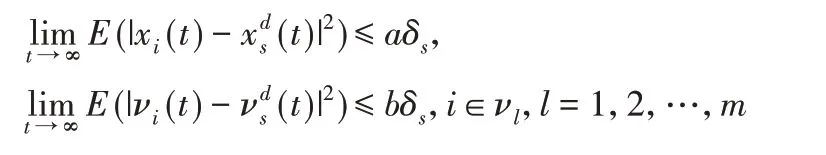
很明顯，不等式右邊為函數δs的單調遞增函數。由定義2可知，系統（1）可以實現多追蹤。

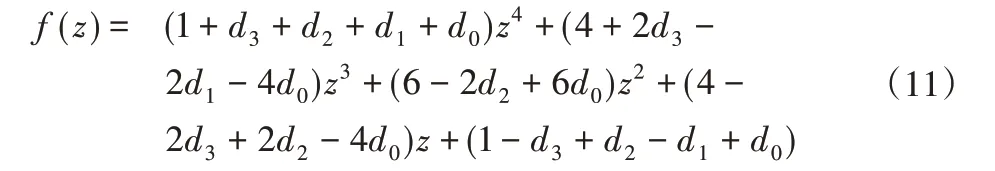
其中，

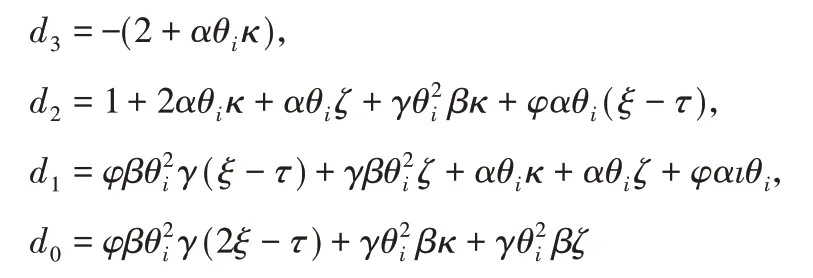
證明：矩陣A的特征多項式為：

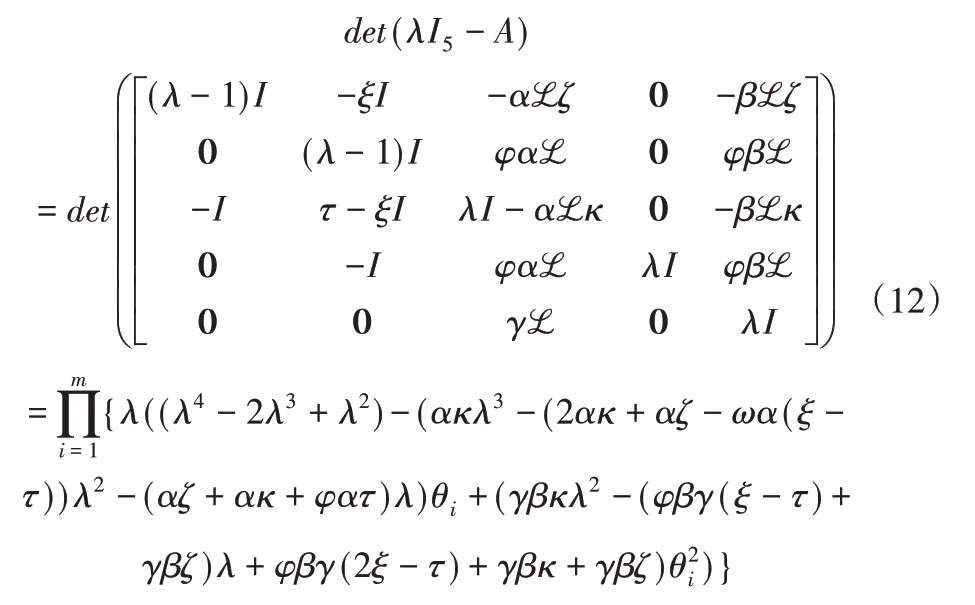
矩陣A的特征值滿足：

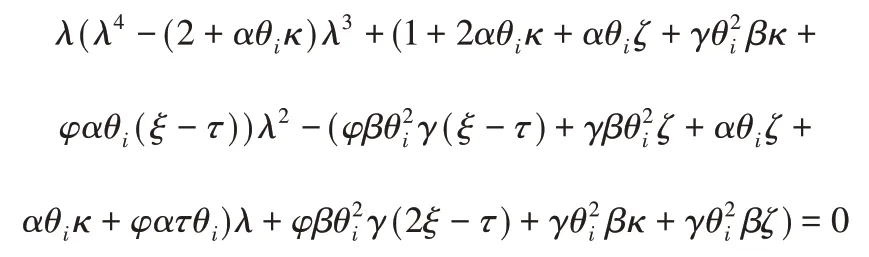
不難發現，對每個給定的θi，都可得五個矩陣A的特征值，其中0為一個特殊的特征值。為了簡化計算，令

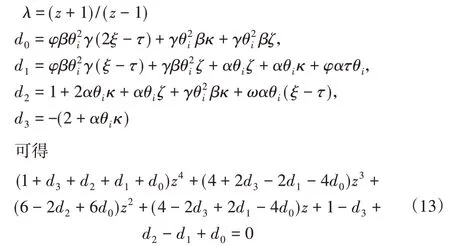
不難發現當且僅當R(z)＜0時ρ(A)＜1，也就是說二階多智能體系統可以漸進到達多追蹤當且僅當多項式（13）時Hurwitz穩定的。

4 案例分析

我們采用具有五個智能體的多智能體網絡，測試所提出的通信時滯下的量化間歇控制協議。網絡的拓撲圖，如圖1所示。將此網絡G劃分為兩個子網絡，兩個子網絡分別為：V1={1，2，3}和V2={4，5}。

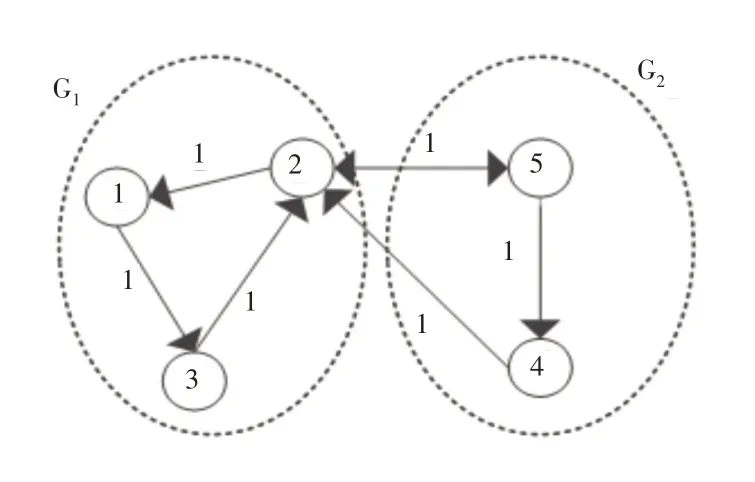
圖1 具有5個節點的多智能體系統的拓撲圖Fig.1 The Topology Diagram of a Multi-Agent System with 5 Nodes

牽制矩陣為B=[0，1，0，0，0；0，0，0，0，1]，也即牽制節點分別為節點2和節點5。Laplacian矩陣L為：

令脈沖函數為η(t)=1，通信時滯為τ=0.05，控制持續時間為ε=0.001，期望軌跡為。選擇控制參數α=5，β=0.4和γ=2。從定理1可得，系統可以現實多追蹤當且僅當0.1 ＜ξ＜3.5。基于控制協議（4），考慮通信時滯為τ，ξ=3.4時二階多智能體系統（1）可以實現多追蹤，如圖2所示。ξ=3.5時二階多智能體系統（1）可以實現多追蹤，如圖3所示。

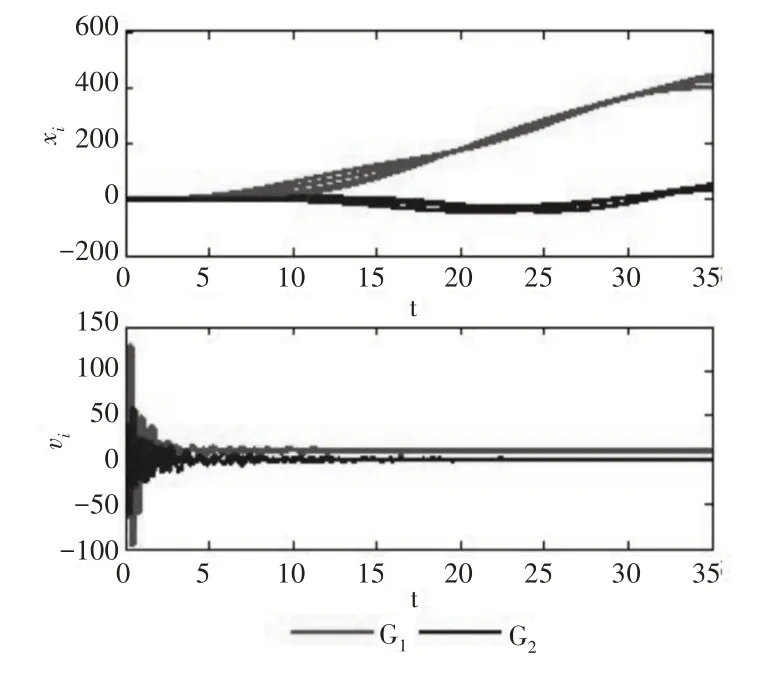
圖2 ξ=3.4時通信時滯下的多智能體系統的多追蹤軌跡。Fig.2 The Multi-Tracking Trajectory of Multi-Agent System Under Communication Time Lag ξ=3.4

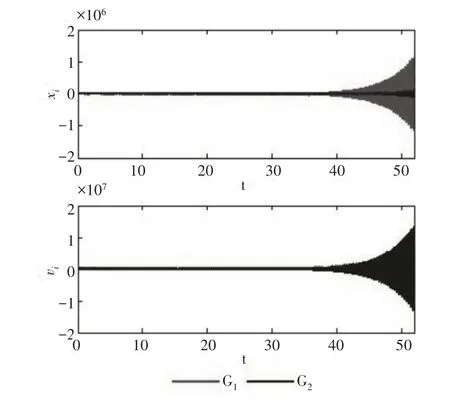
圖3 ξ=3.5時通信時滯下的多智能體系統的多追蹤軌跡。Fig.3 The Multi-Tracking Trajectory of Multi-Agent System Under Communication Time Lag ξ=3.5.

5 結論

針對通信時滯存在下的二階多智能體的多追蹤問題，提出了一個間歇控制協議，此控制協議中每個智能體的控制僅基于采樣位移信息。為了克服通信帶寬的限制，在信息傳輸前，采取隨機量化的方案量化智能體的信息。基于代數圖論、隨機量化和穩定性理論，分析得到了實現系統多追蹤的一些充分必要條件。仿真研究表明，所提出的控制協議可以保證每組中的智能體狀態趨同于領導者的軌跡，另一方面不同組之間互不影響。最后，數值案例研究證實了所提出的間歇控制協議的有效性。將來，我們將考慮不同通信時滯的范圍，完善系統的多追蹤問題，提出的控制方案也可以應用于更多的案例。