“四何”模式下離散數學的教學實踐探索
——以歐拉圖為例

覃雪清

(桂林信息科技學院，廣西 桂林 541004)

離散數學作為一門與計算機及其相關專業的一門專業必修課，在計算機理論及軟硬件開發的各個領域都有著廣泛的應用。計算機相關專業學生的知識技能及相關行業的開發研究都與之有著密不可分的聯系[1]，同時學生抓住事物本質的能力和嚴密的邏輯思維方式離不開離散數學的學習，但是離散數學的課程學習有一定的難度。該課程內容主要包括集合論、數理邏輯、代數和圖論四個相對獨立的模塊。其理論性強、內容豐富、高度抽象以及邏輯嚴密的課程特點會大大地降低學生的學習興趣。同時模塊之間內容繁多，內容相對獨立的特征導致學習過程中無法形成合理的知識概念地圖，學生無法將前后知識聯系起來，增加了課程學習難度。針對此課程的特點，文章提出“四何”學習模式，以期能夠增加學生的學習興趣，能有助于離散數學的學習。

何為“四何”理論？周瑩教授基于系統論和連貫性理論，提出“從何？→是何？→與何？→如何？→變何？→有何？”的認知方法論[2]。周瑩教授的“六何”理論在很多文章和實踐中得到了應用，如：張國玭就高中數學特點在 “六何”理論基礎上進行了創新，提出“六何三線”理論的課堂教學模式[3]，該模式有利于提高學生數學成績以及培養了學生的自省能力；周瑩、黃翠平在“基于“六何”認知策略的數學教學反思—以平方差公式為例”中提出 “六何”認知策略[4]，此認知策略在保障教師的教學反思體系理論性和指導性的同時，還可以有效地形成教師的反思教學系統。

為更清楚明了地闡述“六何”理論，以如圖1所示的框架圖表示“六何”。

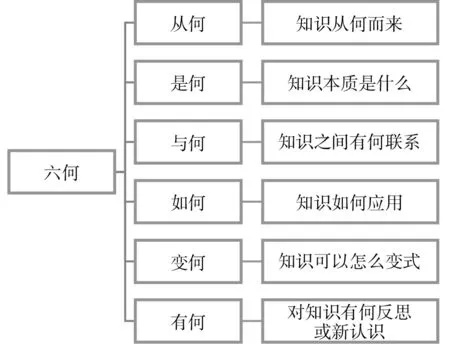
圖1 “六何“理論基本框架

從周瑩教授的“六何”理論以及文獻[3]、[4]中“六何”理論的應用得到啟發，并結合離散數學的課程特點，在初階的離散數學學習中，教師更關注其中的“四何”，即“從何→是何→如何→有何”。參考曾紅中“結構教學+專題教學”教學法[5]文章以離散數學中歐拉圖為例，對“四何”學習模式進行具體分析。

一、“從何”

在學習任何新的知識點之前，學生都應了解知識點的來源及其發展歷程，也就是“四何”理論中強調的“從何”。瑞士數學家歐拉在研究哥尼斯堡七橋問題[6]時最先形成歐拉圖的概念。哥尼斯堡的一個公園里，七座橋a,b,c,d,e,f,g將普雷格爾河中兩個島A島與B島及陸地C，D連接起來，即如圖2所示。問題是：能否從A，B，C，D任一地點出發，有且僅一次通過每座橋并能成功回到原點？歐拉采用“現實—數學”的建模手段經過探索于1736解決了著名的七橋問題，由此開啟了圖論—歐拉圖的這一數學分支。歐拉把該問題歸結為三個字，即能否對圖形進行“一筆畫”，也就是將現實生活中的七橋問題抽象成數學圖形，這個便是數學模型構建的過程。歐拉此舉架構起了現實與數學之間的橋梁，并且歐拉成功地利用圖3證明了上述所說的“一筆畫”走法是不可能實現的。

圖2 七橋示意圖

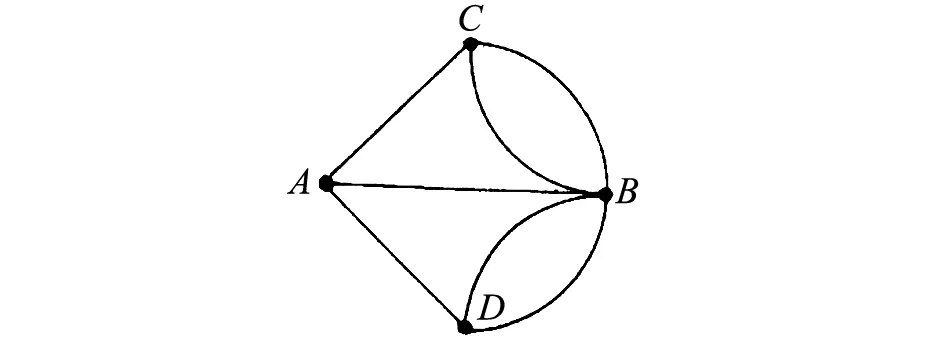
圖3 七橋問題圖形

在學生學習歐拉圖之前，需先了解歐拉圖的來源，即知識點的來源，了解一定的知識背景，知其源方得其法。這樣不僅能夠提高學生的數學素養，還能幫助學生進行知識點的記憶，對于后續給出的歐拉圖的概念能加深理解。在進行歐拉圖的學習之前，可以以這個趣味小故事引入，從而誘導學生的思考——滿足什么條件的圖可以從某一個點出發有且僅經過每一條邊還能回到起點？經過圖中每條邊一次且僅一次的回路稱為歐拉回路，含有歐拉回路的圖被定義為“歐拉圖”[6]。

二、“是何”

由“從何”學生已經對歐拉圖這個概念印象深刻，并且誘發了一系列問題，即什么樣的圖才是歐拉圖，是不是所有的圖都是歐拉圖，是否存在一個方法能夠簡單且快速地判斷出圖形為歐拉圖？接下來進行“是何”環節，即需要探索知識點的本質是什么，包括歐拉圖的含義，歐拉圖的判定方法及其證明方法。由上易知，圖形有兩大要素，即邊和結點。要進行深入研究歐拉圖及其性質特點，那么便離不開這兩大要素。為了更好地探尋知識點的本質，首先應該了解以下兩個定義。

定義1[7]：以結點v作為端點的次數稱為結點v的度數，記為deg(v)。

定義2[7]：從結點v出發回到結點v的路徑稱為v的一條回路。

由上，給出了歐拉圖的概念，即如果一個圖形存在一條經過圖中每條邊有且僅有一次的回路，那么這類圖形稱為歐拉圖[7]。如何快速判斷一個圖形是否為歐拉圖呢？經過對歐拉圖的不斷深入研究，得到相對完美的答案——無向連通圖為歐拉圖當且僅當所有的結點度數均為偶數[7]。利用此結論可以判斷圖2是否為歐拉圖：

deg(A)=3，deg(B)=5，

deg(C)=3，deg(D)=3

由上可知，每個結點度數均為奇數，不符合條件，即七橋圖不是歐拉圖。學生可以按上述結論再進行判斷下圖是否為歐拉圖。

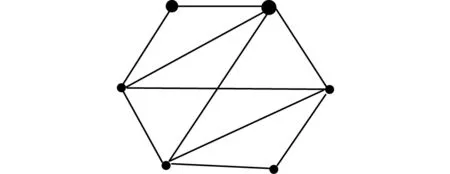
圖4 圖的示例

三、“如何”

在經過“從何”與“是何”后，到了“如何”，即如何利用已學知識應用到現實生活中。歐拉圖的運用非常廣泛，而中國郵路[8]就是其中一個典型的應用。我國數學家管梅谷于1962年首先提出中國郵路問題，并得到了此問題的一種求解方法。該問題是，郵遞員從郵局出發在他管轄范圍內投遞郵件，然后回到郵局。顯然，郵遞員必須且至少經過他管轄范圍內的每一條街道一次，并希望能找到一條盡可能短的路線。如果將此問題抽象成圖論問題，就是給定一個連通圖，連通圖每條邊都有權值(距離)，如果這個圖是歐拉圖，那么便能夠尋找到其中的一條歐拉回路；如果這個圖不是歐拉圖，那么現實中郵遞員就重復走某些邊。將這些重復的邊抽象成圖論中的邊，則是以平行邊的形式出現，重復走幾次，就添加幾次。則把這樣的問題轉化為：在一個含有奇度數結點的賦權圖增加一些平行邊，使得原圖不再含有奇度數結點，并且增加的邊總權值最小[9]。這樣的做法就完成了由非歐拉圖到歐拉圖的轉變。變成歐拉圖后，再利用Fleury算法[10]，即可找出歐拉回路。以下附上Fleury算法：

設G為一無向歐拉圖，求G中的一條歐拉回路算法為：

1.任取G的一個頂點v0為起始結點，并令L0=v0；

2.設已選好的簡單通路為L0=v0e1v1e2v2…eivi，按下面的方法從E-{e1,e2,e3,…,ei}中選取邊ei+1(ei表示圖G中的邊，E表示圖中G的邊集，G′為從G中刪除邊集{e1,e2,e3,…ei}得到的圖)；

(1)結點vi是邊ei+1的端點；

(2)除非無其他邊可選擇，否則刪除邊ei+1不應該改變圖G′的連通性。

3.當2不能進行時(所有邊已選擇)，算法停止。其中，ei表示圖G中的邊，E(G)-{e1,e2,e3,…,ei}

四、“有何”

每一次的學習都應該貫穿“反思”，古人有云，吾日三省吾身，不僅為人處世上需要反思，學習也需要反思和總結。從上述的學習中，有什么收獲？有何感受？還有什么困惑嗎？若存在困惑，下一步該怎樣解決這個困惑呢？由歐拉圖概念的給出，其實很容易思考出另一問題，也就是離散數學中繼歐拉圖后另一類經典圖—哈密頓圖。歐拉圖是至少存在一條走遍所有的邊并且不走相同邊的回路的圖，那么如果存在一條經過圖中所有結點有且僅一次的回路的圖又稱為什么圖呢？這樣的圖是否一定存在？顯然，這類圖是存在的。如果存在，能否也如歐拉圖一般存在一個簡單的判斷此圖的方法，這類圖在現實中又有什么樣子的應用呢？由上述反思過程可知，學生不斷地對知識點進行整理學習不僅可以獲得更深層次的知識點，并在此過程中無形增強了學生思維力度和高度并提高學生歸納的能力，而且能夠引發新的知識點—哈密頓圖[11]。從而，在學生對離散數學中的圖論這一模塊形成了一個基本的知識體系，知識點也不再枯燥無味、孤立離散。參照歐拉圖的“四何”學習模式，學生可以繼續學習哈密頓圖。在這個以老師為輔，學生為主構建知識體系過程中，學生不僅獲得了新的知識點，并且情感體驗上有很強的滿足感，從而有更大的興趣去進行更多的知識探索。從這一反思過程中，不斷對自身知識進行管理和添加新的知識點，從而形成一個龐大的知識體系，為后續學習和工作做好準備。

結語

文章以歐拉圖這個知識點為例，具體講解了如何利用“四何”理論進行學習，不僅適用于學生的學習，也適用于老師的備課。希望“四何”學習模式能夠給予學生學習上的一些啟發，能夠有效高效地進行學習，學會融會貫通，舉一反三。進而也得到一個啟發，“四何”學習模式不僅僅可以應用于圖論的學習，也適用于其他學科的學習中。給出以下的思維導圖(圖5)以便更好地表達文章中心內容。

圖5 歐拉圖的“四何”學習模式

由圖5可知，“四何”學習是一種相互滲透，相互影響又屬層層遞進的關系。 由“從何”提出問題引發思考，從而探究“是何”，在“是何”獲得知識本質后，解決“如何”，最后收獲屬于自己的知識與學習知識體會—“有何”。這是一個完整的且貼合實際應用的學習方法指導，期望“四何”學習理論能夠給學生在學習過程中一些啟發。