基于灰狼優化算法的混凝土壩變形監控模型

陳淑云,周穩忠,谷艷昌*,王 宏

(1.宜興市橫山水庫管理所，江蘇 宜興 214200；2.南京水利科學研究院，江蘇 南京 210029；3.水利部大壩安全管理中心，江蘇 南京 210029)

改革開放以來，中國水利水電事業發展迅速，水庫大壩建設取得了顯著成就[1]。水庫大壩是優化水資源配置、調度水資源時空分布的重要工程措施。截至2017年，中國已修建各類水庫98 795座，其中大型水庫732座，總庫容9 035億m3；中型水庫3 934座，總庫容111億m3[2]。由于歷史原因，中國水庫大壩多建設于20世紀50年代左右，許多大壩存在防洪標準低、施工質量差等安全隱患問題。隨著時間的推移，大壩出現了不同程度的老化和病變問題，存在諸多安全隱患，隨時威脅著下游城鎮人民的生命財產安全。

為實時掌握大壩運行情況、判斷大壩安全性態，目前最有效的辦法是對大壩進行安全監測，并對監測數據進行分析[3]。其中大壩變形監測資料能最直接的反映大壩運行狀態，變形監測資料數據分析方法分為定性和定量分析，主要是通過研究其時空分布規律，運用數學分析方法建立變形量及其影響因素之間的數學模型，預測變形發展趨勢，評估大壩服役狀態。常見數學模型包括統計模型、確定性模型、混合模型，統計模型是利用監測序列資料，通過數學回歸計算方法，估計監控模型的待求參數，進而建立統計監控模型。確定性模型是用有限元法對計算值與實測值進行最小二乘法擬合，建立了可靠的高精度模型，吳中如院士首次在國內將確定性模型用到佛子嶺拱壩壩頂水平位移分析中[4]。混合模型則是水壓分量用有限元計算值，其他分量用統計分量而建立[5]。近年來，人工神經網絡和支持向量機等方法發展迅速[6-7]，逐漸被眾多學者運用到大壩監測數據分析中來，并將神經網絡與各種算法相結合[8-9]，使大壩安全監測資料研究體系更加完善和全面。李月嬌等[10]運用改進的自適應遺傳算法對參數進行尋優，全局搜索能力更強，泛化能力更好，進一步提高了模型擬合效果和預測精度。隨著新型種群智能仿生算法的發展，如粒子群算法、蟻群算法、蜻蜓算法等[11]，進一步推進了大壩變形監控模型的發展，這些算法在模型的擬合效果和預測精度方面效果較好，相較于傳統的數學回歸方法優勢更大。

灰狼算法(Grey Wolf Optimization， GWO)是Mirijalili等[12]通過研究狼群生活習性，于2014年提出的一種具有競爭性的新型群體智能優化算法。現有研究表明，灰狼算法具有復雜度低、控制參數少、搜索能力強、效率高等特點，在求解精度和穩定性上具有明顯優勢[13]。目前GWO算法已成功應用于電力系統、經濟調度指派、車間調度等[14-15]。本文引進灰狼算法分析某混凝土重力壩變形測點監測數據，進一步優化大壩變形模型。

1 灰狼算法(GWO)基本原理

灰狼是大自然界中頂級食肉動物，通常被視作頂級殺手并且處于食物鏈的最頂端。狼群具有嚴格的等級制度和分工制度，可描述為金字塔等級制，將灰狼群體分為4層：α、β、δ和ω層，見圖1。

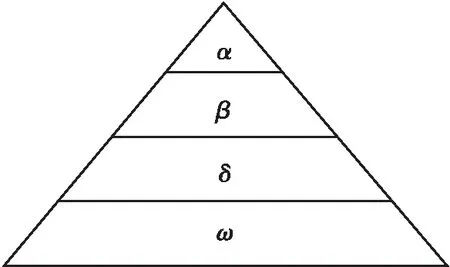
圖1 灰狼等級金字塔

每個狼群里灰狼的平均數量為5～12頭。在灰狼算法中，等級最高的是頭狼，被標記為α，是狼群的主要管理者，負責狩獵、狼群的決策以及整個狼群的領導。β層狼的主要功能是當頭狼α位置空缺時，β則頂替成為α，具備頭狼α的權利，支配狼群中其他成員的活動。下一層狼稱為δ，δ聽從α和β的指令。金字塔最底層狼稱為ω，主要負責種群內部關系的平衡。狼群中下一層級必須嚴格服從上一層級的領導，并進行群體狩獵行動。

灰狼算法的主要靈感來源是灰狼群體嚴格的社會等級制度以及灰狼的狩獵方式。灰狼群體的捕食行為分為包圍、獵捕以及攻擊3步驟。

a)包圍。狼群捕食狩獵首先是對目標進行包圍，確定狼群個體與待捕獵物之間的距離，數學模型可以描述為：

(1)

(2)

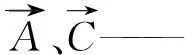
(3)

(4)

b)捕獵。在狼群對獵物實施包圍后開展捕獵行動，在捕獵過程中通常由α、β、δ的位置模擬灰狼的狩獵行為進行位置更新，在迭代過程中保存歷史的前3個最優值(即狼群狩獵最優位置)，種群中其他灰狼群通過最優值的位置更新而不斷更新自己的位置。灰狼群在進行狩獵時數學表達式描述如下：

(5)

(6)

(7)

(8)

(9)

(10)

(11)

由式(5)—(7)確定群內個體與α、β、δ的距離，然后由式(8)—(10)可以確定更新后的灰狼位置，由式(11)可確定獵物所在位置。灰狼算法最優解向量位置更新過程見圖2。

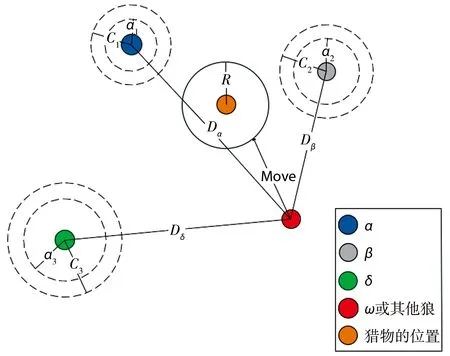
圖2 GWO中灰狼的位置更新過程

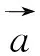
2 灰狼算法(GWO)的計算流程

通過前文對灰狼優化算法包圍、捕獵和攻擊3步驟的闡述，總結出灰狼優化算法的大致計算步驟。

a)設置灰狼算法各參數數值：灰狼狼群的規模N，最優解求解總迭代次數tmax，待求變量的取值范圍，隨機生成α、A、C等參數、初始化灰狼種群位置。

b)計算N個個體灰狼所處位置的適應度值；選擇3個位置適應度值最好的灰狼，記錄其位置向量為Xα、Xβ和Xδ。

c)用式(5)—(11)更新其余灰狼的位置。

d)用式(3)—(4)更新參數α、參數A和參數C。

e)重新計算狼群個體的位置適應度值，與上一次計算結果相對比，重新選擇個位置適應度最好的灰狼作為下一代，判斷結果是否已滿足條件，如果不滿足條件則重復進行(2)—(5)，繼續進行迭代計算。若迭代次數達到設定的最大迭代次數tmax，停止尋優計算。

根據灰狼優化算法操作步驟，繪制GWO流程，見圖3。

3 工程實例

某水利樞紐工程由攔河大壩、右岸地下電站廠房、左岸岸邊通航建筑物及灌溉渠首工程等建筑物組成，水庫總庫容17.41億m3，屬于大(1)型水利工程，防洪庫容7.4億m3，為年調節水庫。大壩為碾壓混凝土重力壩，最大壩高131 m，壩頂寬12 m，總長368 m，壩頂高程245 m。大壩布置了視準線、引張線、倒垂線、正垂線、裂縫計和測縫計等監測設施。

3.1 建模

選取3號壩段2013—2014年壩頂變形監測數據作為訓練樣本進行分析，剔除異常數據后保留71組位移監測數據，將1—11月共65組數據作為模型訓練樣本，12月份6組數據進行預報分析。

大壩壩頂位移與水位值、溫度量和時效值之間的關系見式(12)。

(12)

式中H、H0——監測日和始測日的上游水頭，m；t、t0——監測日和始測日至時間起算日的累計天數，d；θ、θ0——監測日和始測日至時間起算日的累計天數t、t0除以100；αi、b1i、b2i、c1、c2——各效應分量的回歸系數；α0——常數項。

設置狼群個體N=10，待求系數范圍為[-1～1]，求解總迭代次數tmax=100，通過自編灰狼算法程序，建立大壩變形模型目標函數。

為了對比模型精度與預測效果，同時運用逐步回歸法和BP神經網絡進行變形模型的擬合以及結果預測[16]。

灰狼優化算法和逐步回歸法擬合結果見表1，根據模型擬合和BP神經網絡計算結果，繪制實測變形值、GWO模型變形值、逐步回歸模型變形值和BP神經網絡擬合變形值過程線和殘差過程線，見圖4、5。

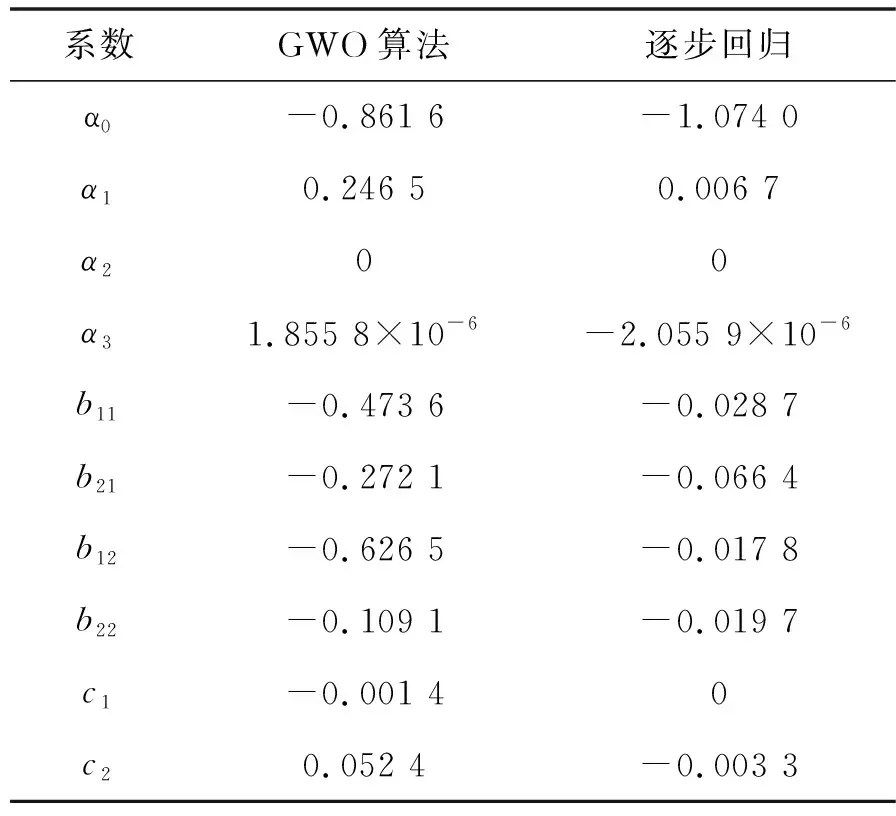
表1 回歸分析結果

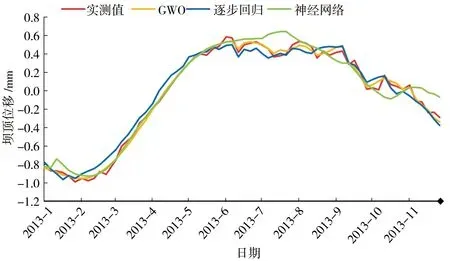
圖4 實測、GWO、逐步回歸和神經網絡變形值過程線

圖5 GWO、逐步回歸和神經網絡變形殘差過程線

3.2 模型擬合效果評估

為衡量計算模型精度，采用復相關系數R進行判別，具體公式見式(13)。

(13)

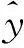
復相關系數R越大，表示因變量與自變量線性組合的密切程度越好，統計模型建立的因變量與自變量之間線性關系越好。一般認為當復相關系數R≥0.80時，實測值與回歸值的偏差較小，回歸模型的精度較高，擬合結果滿足要求。

經計算，GWO模型的復相關系數為0.990，逐步回歸模型復相關系數為0.946，BP神經網絡擬合結果復相關系數為0.973。三者精度都滿足要求，但是GWO模型相比于逐步回歸模型和BP神經網絡擬合效果更好，更符合實測值變化情況。

3.3 模型預測評估

為進一步評估模型的準確性和適用性，根據計算模型和BP神經網絡預測12月份的位移值，實測值與預測值結果見圖6。

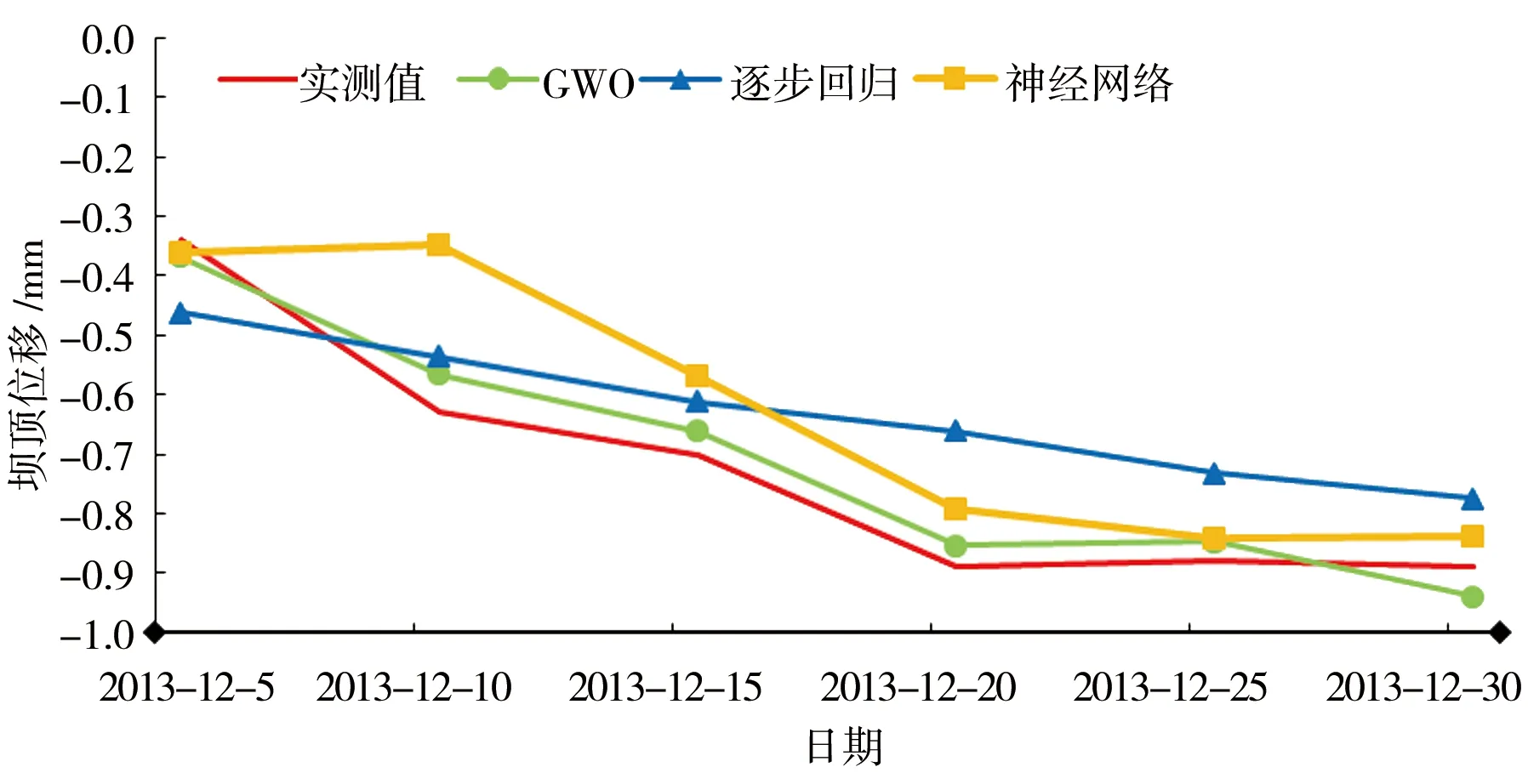
圖6 GWO、逐步回歸和神經網絡變形預測值與實測值

采用平均絕對誤差MAE和均方根誤差RMSE評價模型預測的精度，具體公式見式(14)、(15)。

(14)

(15)

MAE與RMSE值越小，則表示模型預測精度越高，計算結果見表2。

表2 MAE和RMSE計算結果統計

根據圖6以及表2可知，相比于傳統逐步回歸模型和BP神經網絡，GWO模型預測變形值結果更符合實際情況，預報誤差更小，驗證了GWO模型在大壩變形擬合和預報過程中的適用性。

4 結論

針對大壩變形資料分析建模問題，本文通過研究灰狼算法(GWO)，提出基于灰狼優化算法的大壩變形模型建立方法，并將本算法擬合和預測結果與傳統逐步回歸方法作比較，主要得出以下結論。

a)灰狼算法(GWO)算法作為新型智能算法，具有復雜度低、控制參數少、搜索能力強等特點，用于分析大量位移監測數據，建立位移模型上具有明顯優勢。

b)運用灰狼算法(GWO)算法建立的位移模型相比于傳統逐步回歸分析和BP神經網絡結果，在擬合和預測精度上都得到明顯的提升，驗證了GWO模型在大壩變形擬合和預報過程中的適用性。

c)灰狼算法(GWO)運用中應注意，灰狼狼群的規模一般取值5～15即可，本文取值10所建模型精度已經明顯提高；待求變量的取值范圍，需要依據待求問題實際情況并憑借工程經驗確定或試算，同時調整最大迭代次數，防止算法陷入局部最優。