基于大數據和智能校園的大學生體質研究

羅 明

（江門職業技術學院，廣東江門 529000）

大學生本身不愿意參加體育鍛煉，而且學校對體育課程重視程度較低，課程設置不一致[1]，進一步加劇大學生體育鍛煉不足[2]。因此，對高校大學生體質進行研究并獲取適合的評價方法，具有十分重要的意義。

1 大學生體質現狀

體質與健康密切相關[3]。身體健康以身體指標反映人體的健康狀況。它已成為反映學生群體健康狀況的一個特殊術語。目前，我國大學生的身體素質同步提高程度明顯不足，學生肥胖和超重檢出率繼續上升。因為在我國高校體育教學中，仍然使用舊的、統一的成績來評價和衡量大學生的身體素質，這使得體育課的教學內容十分僵化，教學過程更加單調。因此，它極大地阻礙了學生潛能的開發，也導致學生不重視、不喜歡、不積極參與學校體育課程。

2 建模分析

2.1 數據分類

本文采用SPSS 軟件實現數據統計，再采用Logistic 線性回歸模型完成擬合運算。同時，還增加了智能校園系統中關于學生骨骼發育、血氧指數和運動功能的數據指標，并發展和擴展為因子組，符號表如表1 所示。

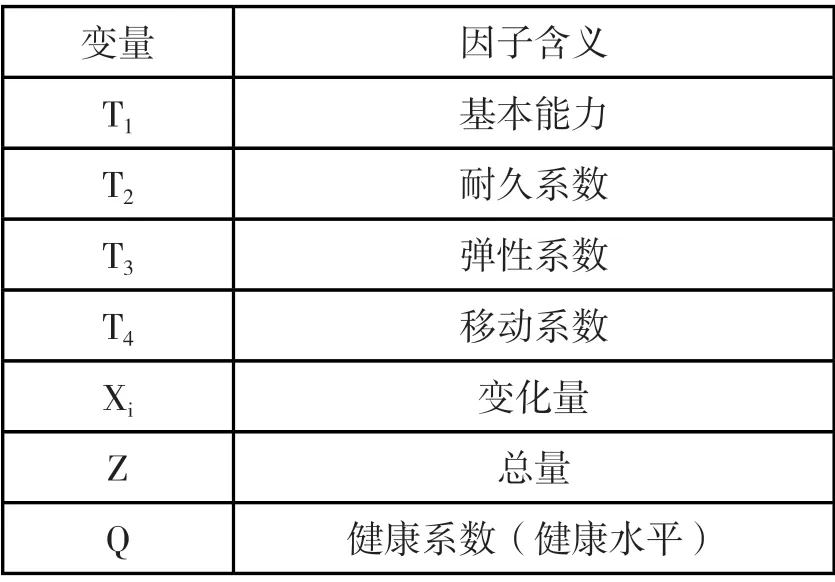
表1 符號表

為消除模型中的不確定性因素，補充測試對總體數據的影響被忽略。

2.2 模型建立

基于上述數據指標，可以開始模型解決方案。為了研究測試者的測試分數與身體狀況之間的關系，首先對指標進行統一量化，然后將所有數據輸入SPSS 軟件。身高、體重得分和肺活量得分相加，如等式（1）所示：

在公式（1）中，XS 和XT 是指身高體重分數和肺活量分數，它們是基本能力因素的值。耐力、柔韌性和柔韌性項目都有很好的分數，可以直接使用。如果該系數包含多個變量，則應使用上述等式將變量分數組合成一個百分比系統。

有必要找出每個因素與學生體質之間的關系，并找出每個因素之間的權重值。輸入SPSS 軟件后，將T1～T4的KMO球面檢驗結果與球面檢驗相結合，得到總因子的方程（2）：

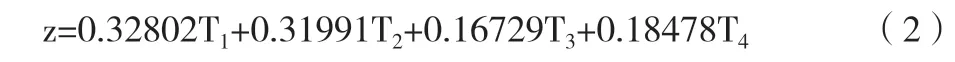
Logistic 線性回歸模型中，模型相關變量為y，獨立變量為xi。在m 個自變量的作用下，預期結果的條件概率為P=P（y=1 | x1，x2，x3…xn），則邏輯回歸模型可表示為：

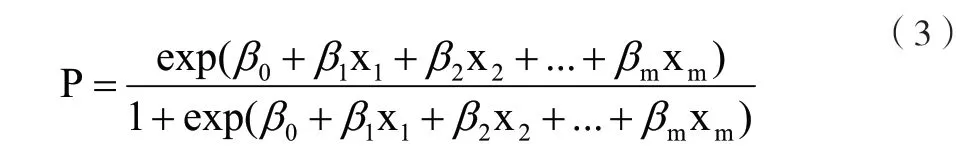
進而Sigmoid 函數可以由下式獲得：

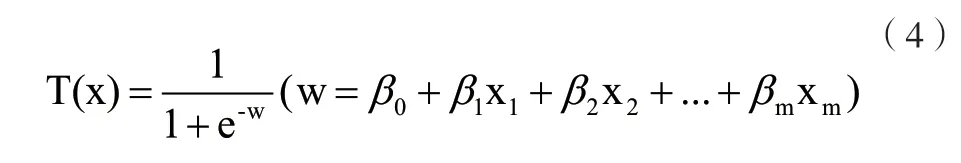
方程（4）的域為（-inf，+inf），取值范圍為（0，1）。間接使用Sigmoid 函數，從而擴展了構建模型的內容。在函數中，由于參數范圍為（0+∞) 這在函數所需的域中是非負的，通過SPSS 可知，每個數據的綜合系數也是非負的。因此，對原始基本方程進行了改進，但由于加權后結果值隨原始結果而變化，因此使用比例方程將綜合因子z的結果控制在[0,10]，也就是說，方程中的所有子變量都與整體變化呈正相關。

建立邏輯模型，其中自變量T1、T2、T3和T4是每個子系數xij的矩陣。權重用于計算總因子z，公式如下：

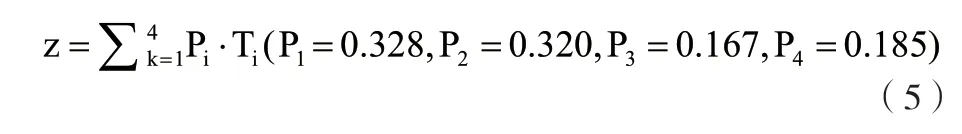
通過對替代模型的計算，得到了Q 和z 方程：

3 數據分析

將學生數據代入大數據進行計算。方程的域是z ∈（0,10），取值范圍為Q∈（0,1）。方程采用Logistic 線性回歸連續迭代計算，初始迭代次數為0.1。此處迭代系數分別設置為0.3、1.8 和2.5。當被測學生的所有因子均為0 時，學生的健康系數為0。隨著自變量的增加，Logistic 模型得到的Q的增長曲線x 迅速上升。使用Matlab 繪制生長曲線圖像，如圖1 所示；以評價等級為0-5，分數值的分布區間如圖2 所示；當評價等級為15-25 時，分數值的分布區間如圖3 所示。

圖1 增長曲線

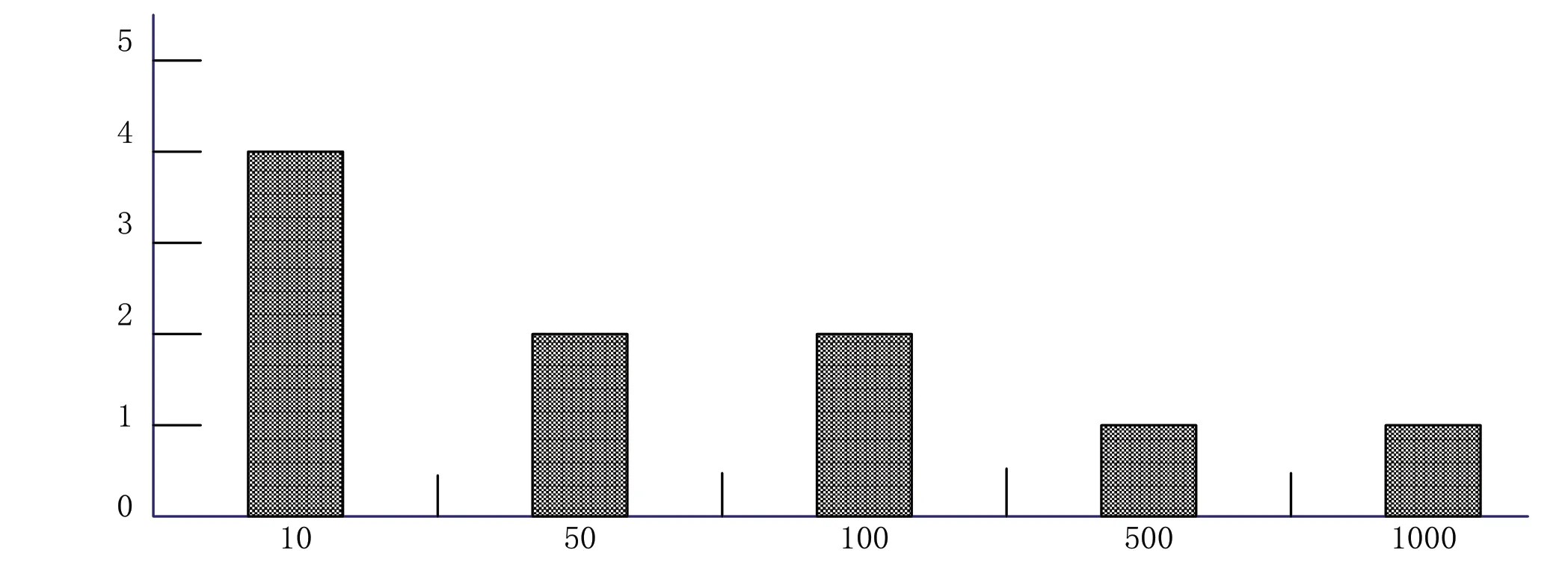
圖2 評價等級為0-5 下的分數分布狀況

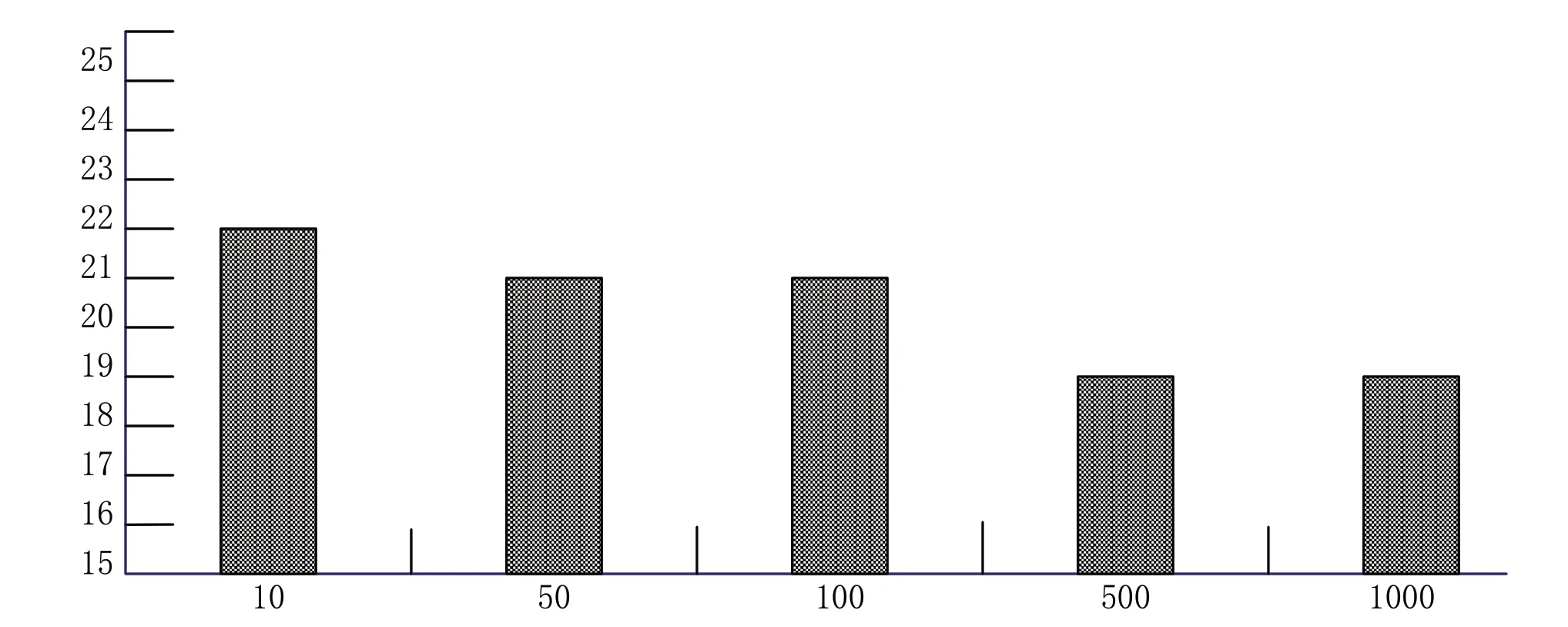
圖3 評價等級為15-25 下的分數分布狀況

4 結論

基于大數據的學生數據測量模型反映了學生的健康狀況。結合智能校園系統的數據指標，可以得出結論，即當分數處于大多數人的水平時，學生的健康狀況很可能是正常的。如果綜合得分略低于多數，可針對學生得分較低的情況予以強調，導師應促進相應的鍛煉，以預防健康風險。當總分遠低于大多數學生時，應引起學校的注意。應跟蹤學生的健康狀況，并提供指導，提升大學生體質健康的整體水平。