一類分數階生態毒理學模型的定性分析

高正暉

（廣東科技學院（松山湖校區）通識教育學院，廣東 東莞 523330）

0 引言

研究環境污染對生物種群的影響是屬于生態毒理學（Ecotoxicology）[1]的范疇，Ecotoxicology這一詞匯是由Truhaut在1969年創造的，它是由毒理學（Toxicology）與生態學（Ecology）結合而成，是毒理學向生態學領域的發展.毒理學通常是研究毒素對生物個體的影響，而生態毒理學則是研究釋放在環境中的毒素對生物種群、群落、乃至生態系統的影響.研究污染環境中種群的生存狀況及其變化規律也隨之成為數學生態學領域中的熱點問題，在20世紀80年代，T.G.Hallam及其同事[2-4]假設種群的增長率線性地依賴種群對毒素的吸收率，建立了環境中的毒素對單種群影響的基本生態毒理學模型：

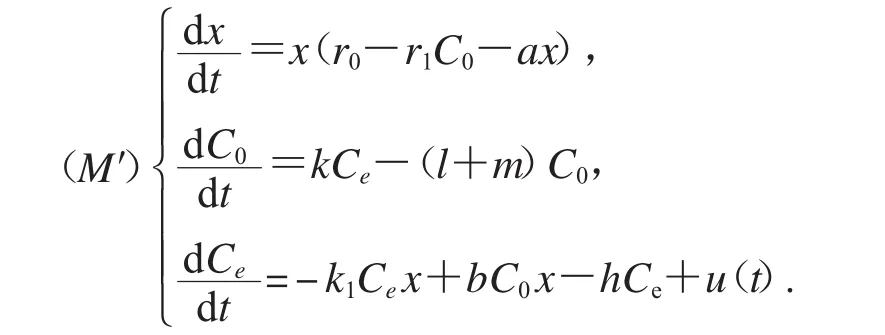
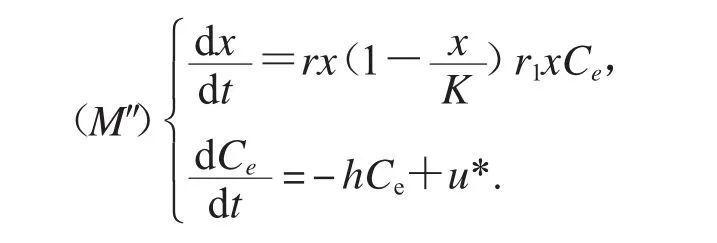
其中x（t）表示t時刻種群的密度，Ce（t）表示t時刻環境中的毒素濃度，r表示無污染時種群的內票增長率，K表示環境容納量，r1Ce表示種群由于吸收了環境中污染物的濃度以后而導致種群減少的劑量反應函數，hCe表示由于生物轉移、揮發、細菌的退化和死亡以及其他等因素所引起的污染物濃度的減少，u*為外界向環境的毒素輸入率.

分數階微積分（Fractional calculus）[9-17]是數學分析的一個領域，它主要研究任意階積分和導數的理論及其應用，是傳統的整數階微積分的推廣，分數階微分方程是含有非整數階導數的方程.近年來，分數階微積分及分數階微分方程理論在物理、化學、生物、環境科學、控制、工程以及金融等許多領域的廣泛應用已引起了相當大的影響，吸引了越來越多的學者關注.因為分數階微分方程比整數階方程更精確的描述了客觀世界，因此對于分數階微分方程的研究，不但具有重要的理論價值，而且還有十分廣泛的應用價值，這些應用極大的促進了分數階微分方程理論的發展.

如今，分數階生態毒理學模型是一個前沿研究課題，若將系統（M″）中的整數階導數用分數階導數替代，就得到了分數階生態毒理學模型：

在這篇文章中，我們的目的是借助數學手段，建立環境中的毒素對單種群影響的分數階生態毒理學的數學模型（M），應用分數階微積分及分數階微分方程理論，并結合微分方程的定性與穩定性分析方法，給出分數階生態毒理學模型（M）在平衡點的穩定性的判定條件.

1 預備知識與引理

本節中我們給出了本文要用到的分數階微積分算子的定義和引理，令C[0，T]，T＞0是定義在[0，T]上的所有連續函數的集合.

2 分數階生態毒理學模型（M）的平衡點與穩定性分析

3 結論