基于GLSAFIS的氟化工過程操作單元可靠性監測

薛峰，李欣銅，周琨，魏志強，葛曉霞，葛志強，宋凱

（1 天津大學化工學院，天津化工安全與裝備重點實驗室，天津300350； 2 蘇州創元產業投資有限公司，江蘇蘇州215000； 3 巨化集團有限公司健康安全環保部，浙江衢州324004； 4 浙江大學控制科學與工程學院，工業控制技術國家重點實驗室，浙江杭州310027）

引 言

氟化工是典型的精細化工過程，其產品在汽車、環保、航空、新能源等領域有著廣泛應用。隨著產品的多樣化和應用領域的不斷發展，氟化工行業變得越來越重要。然而，在氟化工生產過程中廣泛存在著劇毒性材料。這些劇毒物質即使在環境中有少量泄漏，仍會對人員、設備以及公共財產造成巨大危害。隨著現代氟化工生產過程的大型化和復雜化，給氟化工過程監測系統帶來了巨大的壓力。

由于氟化工過程機理復雜，強時變、劇毒等特性加上專利保護等，嚴重阻礙了先進的控制和監測方法在氟化工過程中的廣泛應用。另一方面，隨著這些過程復雜化和大型化，專家知識出現差異的概率越來越高，難以在過程監測方法中應用準確的專家知識。當前，由于上述原因，過度維護策略是氟化工過程安全管理中最常用的策略。顯然，這些方法會導致巨大的經濟損失和安全風險。因此迫切需要提高氟化工生產系統的安全性和可靠性監管力度，從而避免故障甚至重大事故所帶來的巨大經濟損失。傳統的氟化工過程監測系統主要關注氟化工過程故障檢測和診斷方法的研究，而故障檢測和診斷只能在發生故障后對化工系統進行修復和彌補，此時往往已經造成了安全或者經濟損失[1]。此外，隨著健康管理概念的提出，越來越多的研究者意識到，故障意味著過程或者裝備中的部分失效。但是即使未出現故障，也并不意味著系統安全運行的可靠性在最佳狀態。因此本文旨在提出操作單元可靠性評估方法，對系統安全運行狀態進行評估。從而在故障發生前及時采取措施，為實現預測性健康管理奠定基礎。

隨著研究的不斷深入，作為預測性健康管理（PHM）重要的基石，目前主流的可靠性評估方法可以分為三類[2]：基于知識的方法、基于解析的方法和基于數據驅動的方法。其中基于知識的方法受限于生產經驗和專家知識的準確性，基于解析的方法依賴于研究對象的物理、化學原理，而數據驅動模型則通過利用系統中采集到的大量過程數據信息建立黑箱模型以實現過程監測。所有這三類方法中，最基本的方法是可靠性框架圖（reliability block diagram，RBD），但是該方法只允許評估對象有兩個狀態：完全可靠和完全故障。然而在大多數情況下，評估對象的狀態不限于二值狀態[3]。其他用于可靠性評估的方法包括故障樹分析、蒙特卡羅模擬和貝葉斯網絡等[4-7]。Rebello 等[8]通過動態貝葉斯網絡和隱馬爾可夫模型對系統功能可靠性進行評估。BahooToroody 等[9]利用貝葉斯回歸方法監測能源供應中隨機過程的可靠性。Wang等[2]使用云推理方法研究多故障交互狀態的管道系統可靠性。大多數可靠性評估方法都依賴于專家知識，只能局限于評估特定對象的可靠性。且當前的可靠性理論主要針對特定的電氣設備、電子、航空、能源等領域，化工領域由于變量多、強耦合、強時滯和非線性等特性，相關研究較少，相關應用則更少。

與多元統計過程監控（multivariate statistical process monitoring，MSPM）方法不同，模糊推理系統（FIS）可以通過指定隸屬函數和模糊規則來集成數據驅動進行建模[10]。此外，其成功應用還歸因于對不精確數據的計算優勢[11-12]。FIS 在控制系統、工程、醫學、化學、金融和商業、計算機網絡、計算生物學、故障檢測和診斷以及模式識別等研究領域中的廣泛適用性充分證明了它的優越性[13-15]。對于諸如氟化工過程之類的復雜的化工過程，FIS 具有很好的應用前景。然而，FIS 過于依賴專家知識，且對于大型化工過程等變量較多的研究對象，所需設計的模糊規則過多，FIS的實用性較差。

另一方面，氟化工過程數據樣本中包含了豐富的結構信息，對這些結構信息的抽提和轉換是實現評估氟化工過程可靠性算法的重要因素。主成分分析等算法在提取樣本空間結構特征時只考慮了整體結構[16]，局部結構保留投影等流形學習算法主要關注樣本空間的局部結構信息。而全局-局部結構分析算法在同一框架下統一了兩種算法的優勢，使得投影得到的低維空間不僅保持了原始數據的局部結構，而且保持了相似的整體結構，原始數據更加全面的特征信息得已保留。

因此本文充分利用FIS 對于復雜系統不確定性的魯棒性和邏輯推理能力，針對氟化工過程變量體量大、變量間強耦合、強時變和專家知識不確定度高等特點，提出了基于全局-局部結構分析的模糊推理系統（global-local structure analysis based fuzzy inference system，GLSAFIS）對氟化工過程關鍵操作單元的運行狀態進行可靠性評估。依據氟化工工藝流程選取操作單元過程變量，通過全局-局部結構分析算法對操作單元過程變量進行全局-局部特征提取。將低維的全局-局部特征代替原始操作單元過程變量作為模糊推理系統的輸入，在減少數據噪聲的同時可以通過降維，大大減少所需設計的模糊規則和對專家知識的依賴，加速后續模糊推理系統的邏輯設計。因此本方法能夠充分考慮到過程變量對操作單元運行的影響，依據氟化工過程數據對操作單元的可靠性進行實時評估，從而為實際生產過程安全管控提供實時可靠的決策依據，以減少甚至避免故障的發生。真正實現維護策略從傳統的故障檢測和診斷（fault detection and diagnosis，FDD）轉向預測和健康管理（prognostics and health management，PHM）[17-19]。在國內某氟化工廠R-22生產過程以及模擬化工過程TE模型中應用，以證明本方法的有效性。

1 基于全局-局部結構分析的分布式并行模糊推理系統

1.1 變量選取及特征提取

氟化工過程的操作單元之間具有強烈的耦合性，每個操作單元的波動都不可避免地影響其下游的操作單元。因此，在選取操作單元過程變量時，應當充分考慮到操作單元本身的過程變量情況以及上游操作單元中可能會對其產生影響的過程變量。值得注意的是，選取過程變量不代表每個變量只能劃分到某一個操作單元中。考慮到后續GLSA算法在全局-局部投影方面的優勢，為了充分保留變量間的相互關系，本文的操作過程變量選取時，依據是氟化工工藝流程的上下游關系，允許某些變量同時屬于多個操作單元。例如上一單元的輸出作為下一單元的輸入，此變量可同時屬于這兩個單元的數據模塊。

為了進一步克服過程數據的高噪聲特性，降低數據維度，提高FIS 邏輯設計的效率，同時減少邏輯設計對專家知識的依賴，本文引入了GLSA 算法，對每個數據塊進行特征提取。全局-局部結構分析算法不僅可以有效降低數據維度，而且通過投影得到的低維空間保持了原始數據的整體結構和局部結構。因此提出使用全局-局部結構分析方法對操作單元過程變量進行降維，從而加速后續模糊推理系統的設計邏輯。

GLSA 是在局部保留投影（locality preserving projections，LPP）算法基礎上發展而來的一種無監督降維方法[20]。LPP 是一種常見的線性流形算法，該算法的主要特點是在降低數據維度的同時，力求維護數據集的局部結構和幾何特性[21-23]。下面簡要介紹LPP算法的基本思想。

假設原始數據集為X=[x1,x2,…,xn]?Rm，LPP 的目的就是訓練得到一個投影矩陣A，可以將樣本空間X投影到一個子空間Y=wTX=[y1,y2,…,yn]?Rd。投影矩陣A可以通過求解最小化兩個樣本之間的額加權距離之和得到，LPP 的目標函數為：

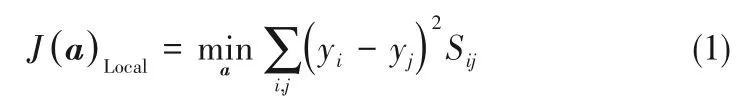
其中，權重系數Sij是鄰接權重矩陣S中的元素，Sij表示原始高維樣本中的xi和xj距離接近程度。因此，如果樣本xi和xj在原始空間中相對接近，它們在投影后的空間也會相對接近。

雖然通過優化LPP的目標函數可以確保原始空間中接近的點在投影之后能夠保持接近，但是LPP對于原始空間中互相遠離的點沒有相應的約束條件，這會使這些點被投影到一個很小的區域中，從而導致數據集的全局結構的破壞以及方差信息的損失[24-25]。GLSA 有效解決了這一問題，在LPP 的基礎上引入了全局結構的優化目標函數：

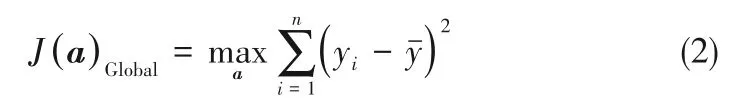
GLSA的目標函數定義為：

式（3）可以轉換為如下的特征值分解問題：

通過求解M的前d個最大特征值所對應的特征向量，即投影矩陣A=[a1,a2,…,ad]，可以得到低維投影空間：

將降維后得到的低維投影變量作為操作單元可靠性估計的依據，這樣不僅可以保留原始過程變量數據的全局和局部結構，而且可以大大降低操作單元可靠性估計的難度，大多數研究工作都是保留了前兩個最大特征值[20]，為盡可能多地保留原始數據的全局和局部結構，本文中均保留前三個最大特征值，即將操作單元變量降到三維。

1.2 操作單元模糊推理系統設計方法

20 世紀60 年代，Zadeh[26]首次提出了模糊理論。該理論從數學角度分析研究帶有模糊特征的問題，使得此類問題具有數學特質從而更易被大眾接受。模糊推理系統就是在模糊理論的基礎上發展而來的，它是一種無需復雜的數學解釋就可以對復雜問題建模的工具，可以對通常以語言形式表示的不確定性進行建模。在評估氟化工過程操作單元可靠性時，由于缺乏統一可靠的專家知識以及對機理的深入了解，難以通過具體的過程指標進行評估，模糊推理系統則可以通過融合多元過程指標的信息有效解決這一問題。一個典型的模糊推理系統包括三個階段：輸入階段，處理階段和輸出階段[12,27]。

輸入階段將輸入映射到適當的隸屬度函數得到隸屬度值。隸屬度函數的最常見形狀是三角形，也有梯形和鐘形曲線等。隸屬度函數曲線形狀通常不如數量及其位置重要[28]；處理階段調用每個模糊規則并生成結果，然后組合所有規則的結果。它基于IF-THEN 語句形式的邏輯規則的集合，其中IF部分稱為“條件”，而THEN 部分稱為“結果”。典型的模糊推理系統具有數十條規則；輸出階段將合并的結果轉換為特定的輸出值。

在設計模糊推理系統時，隸屬度函數和模糊規則的設計是最重要的內容[27]。對于隸屬度函數而言，變量等級的確定及每個等級所對應的隸屬度函數曲線的設計是最為核心的兩方面內容。將投影變量劃分為“高”、“中”、“低”三個等級，將操作單元可靠性分為“安全”、“警告”、“報警”和“危險”四個等級。很顯然，當操作單元平穩運行時，投影變量應當處于“中”等級。雖然當投影變量處于“高”或“低”時，操作單元可靠性有可能不受到影響，但考慮到對可靠性評估應當采取更為嚴格的設計方案，所以“高”或“低”的投影變量被認為會影響操作單元可靠性。同樣地，選擇三角形的隸屬度函數曲線確保操作單元可靠性估計設計方法的嚴格性。三角形曲線的具體設計方法：假設操作單元變量降維后的投影變量有d個維度，首先應當確定每個投影變量可接受的波動范圍，從歷史數據中選取操作單元運行時不同時間段的相關變量的數據樣本X∈Rn×m，其中n代表樣本個數，m代表樣本維度，通過GLSA 訓練得到的投影矩陣A將選出的樣本投影到Z∈Rn×d，則樣本矩陣投影后每個投影變量的最小值和最大值之間即為其波動范圍。確定好投影變量波動范圍后，應將其歸一化以符合模糊推理系統輸入的要求：

式中，fi表示模糊推理系統第i個輸入；Zi表示第i個投影變量；和分別表示投影變量Zi的最大值和最小值。隨后應當確定投影變量不同等級下三角形曲線各頂點的位置，同樣地，通過篩選操作單元正常運行時期的歷史數據，通過投影矩陣A將其投影到低維空間，投影后得到的變量的平均值即為該變量的目標值ti，應當將其作為“中”等級的頂點，如圖1所示，將不同等級之間相互交叉的部分占兩等級之間的總距離的比值記為θ=c/d，由θ可以確定其余三角形曲線在底邊上頂點的位置。θ應當根據操作單元的具體情況確定取值，也可以由遺傳算法或者其他優化方法確定。μ為Zi對應的隸屬度值。

圖1 隸屬度函數設計方法示意圖Fig.1 Schematic diagram of membership function design method

模糊規則的設計依據每個輸入變量所處的等級不同確定，表1 列出了每個輸入變量所處的等級以及其是否處于允許狀態。根據實驗結果規定：當沒有投影變量處于“否”，認為操作單元處于“安全”狀態；當有一個投影變量處于“否”，操作單元被認為處于“警告”狀態；當有兩個投影變量處于“否”，操作單元處于“報警”狀態；當全部三個投影變量處于“否”，操作單元則是處于“危險”狀態。舉例來說，如果Z1處于“中”且Z2處于“高”且Z3處于“低”，那么操作單元可靠性處于“報警”狀態。

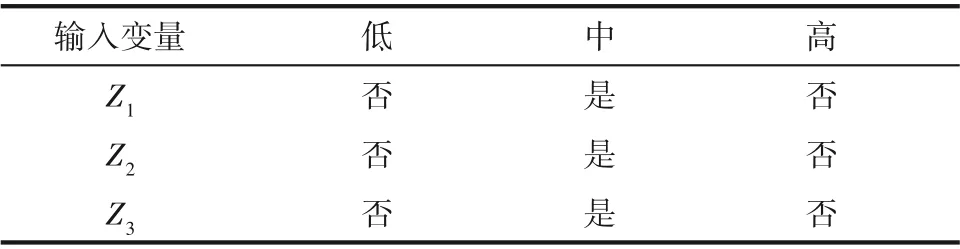
表1 操作單元輸入變量限制條件Table 1 The restriction of operating unit input variables

1.3 基于全局-局部結構分析的操作單元可靠性模糊推理估計

基于全局-局部結構分析的操作單元可靠性模糊推理估計主要包括以下步驟。

（1）選取操作單元過程變量：根據操作單元在氟化工過程系統中的上下游關系，確定影響操作單元操作狀態的相關過程變量。

（2）操作單元過程變量特征提取：選取操作單元正常運行時期的過程變量，訓練GLSA 模型并得到投影矩陣A。

（3）設計操作單元可靠性估計的模糊推理系統：將通過GLSA 模型得到的低維投影變量作為輸入，操作單元可靠性作為輸出，設計模糊推理系統。

圖2 是操作單元可靠性估計流程示意圖，通過基于GLSA 的模糊推理系統的實施，可以評估大規模復雜操作單元的可靠性，從而提供可靠的安全管控決策依據。

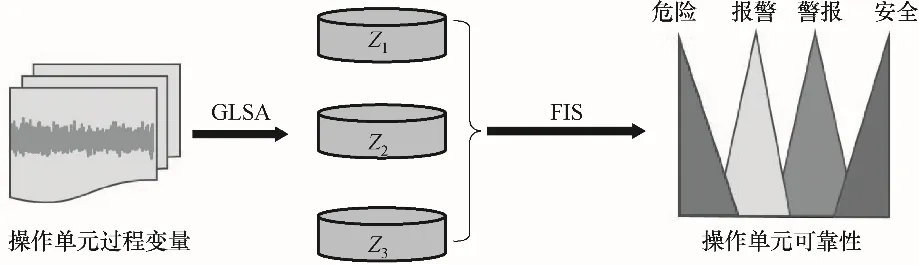
圖2 GLSAFIS算法流程圖Fig.2 Flow chart of GLSAFIS algorithm

2 GLSAFIS方法性能評估

2.1 氟化工R-22過程反應器操作單元可靠性估計

為了測試所提出的GLSAFIS 方法的性能，在國內某氟化工廠R-22 生產過程數據集中應用了本方法。根據保密協議的限制，本文僅以R-22 生產過程的反應器操作單元為例，介紹具體的應用過程及結果。

二氟一氯甲烷，別名R-22，是最常見的制冷劑和推進劑的制作原料，同時也是氟化工的通用中間體。氯仿和氫氟酸是生產R-22 的主要原料，其化學反應方程式為2 HCl，R-22 的生產流程如圖3 所示。R-22 生產裝置由反應器、精餾塔1、水洗塔、分離器以及精餾塔2等操作單元構成。R-22的生產工藝如下：來自裝置外的氯仿以及氫氟酸分別由泵輸送進反應器；氯仿和氫氟酸在催化劑作用下反應生成R-22 以及副產物R-21、R-23和HCl；所有產物及未反應原料、少量催化劑進入精餾塔1，利用分餾原理，分離產品R-22 和副產物R-21 及R-23；冷凝回流的產物經水洗塔洗滌去大部分催化劑、氫氟酸；得到的以R-22 和HCl 為主的粗產品進入精餾塔2 以進一步精餾得到主要產品R-22。

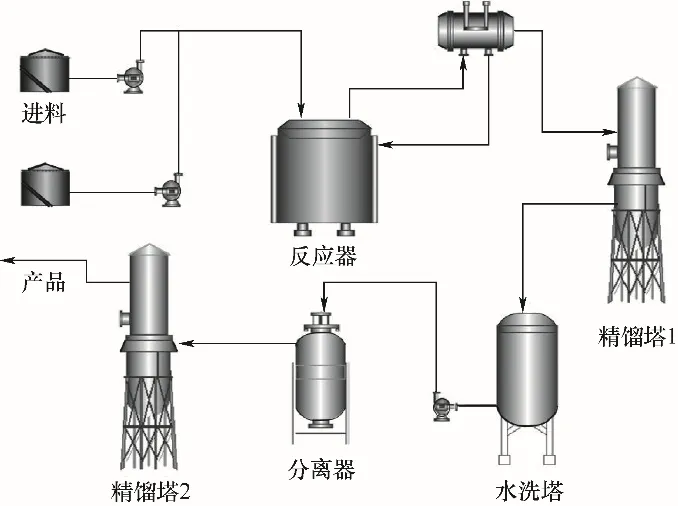
圖3 R-22生產流程示意圖Fig.3 Schematic diagram of R-22 production process

本文所有的氟化工過程數據均來自位于華東的某大型氟化工廠的R-22 生產過程。采樣期為2020年1月至2020年10月，采樣間隔為一分鐘。近一年的采樣周期內包含了數十個原料采購周期，也幾乎涵蓋了當地的四季，因此數據集有很強的代表性。根據保密協議，在研究過程中僅使用了該數據集的一部分數據。如前所述，由于氟化工過程產物的劇毒性，該廠的安全管控非常嚴格，期間有數次常規停車檢修和調試，未出現任何危及到設備、人員和環境的安全事故。為了驗證本文方法的有效性，本文用停車檢修數據模擬非正常生產狀態，進而驗證可靠性評估的準確性。

在進行反應器操作單元變量劃分時，首先將反應器內部的過程變量如反應器溫度、壓力等作為反應器操作單元變量，然后應當考慮與反應器相連接的進料單元的各種進料量及其相關的過程變量。很顯然，進料單元的波動會影響到反應器單元的運行狀態，所以將進料相關的過程變量加入反應器操作單元變量是十分必要的。還需要注意到，反應器單元不僅輸出反應產物，而且通過回流裝置接收精餾后的部分產物，因此，在輸出和回流管道上所獲取的過程變量同樣也應作為反應器操作單元變量。最終，在R-22生產過程的43個過程變量中，共有10個變量劃分為反應器操作單元變量。

選取反應器正常運行期間的1000 個數據樣本并整理出10 個變量所對應的過程數據，訓練GLSA模型，取前三個最大的特征值。其余樣本則可通過投影矩陣A降到三維，將這三個投影變量作為輸入，反應器操作單元可靠性作為輸出設計模糊推理系統，依據1.2 節中介紹的相關設計方法和原則，得到的模糊推理系統示例如圖4 所示，圖4(a)是R-22 反應器操作單元輸入和輸出變量的隸屬度函數，圖4(b)是反應器操作單元可靠性模糊推理的一個示例。

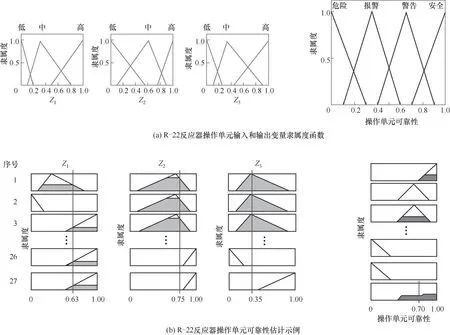
圖4 GLSAFIS在R-22反應器操作單元中的應用實例Fig.4 Application example of GLSAFIS in R-22 reactor operation unit

圖5為三種異常工況下一種重要原料的進料量以及反應器操作單元可靠性，重要原料的進料量一定程度上反映了反應器單元的運行狀況。在案例1中，初始階段重要原料的進料量保持在目標值附近，此時反應器操作單元可靠性也處于90%以上，隨后重要原料進料量出現大幅下降（常規的停車維護而非安全事故），反應器操作單元可靠性也立刻下降到20%附近。隨著重要原料進料的恢復，反應器操作單元可靠性也逐漸恢復到90%以上，但由于重要原料進料量穩定在目標值以上，反應器操作單元可靠性也在安全控制限（80%）附近波動。

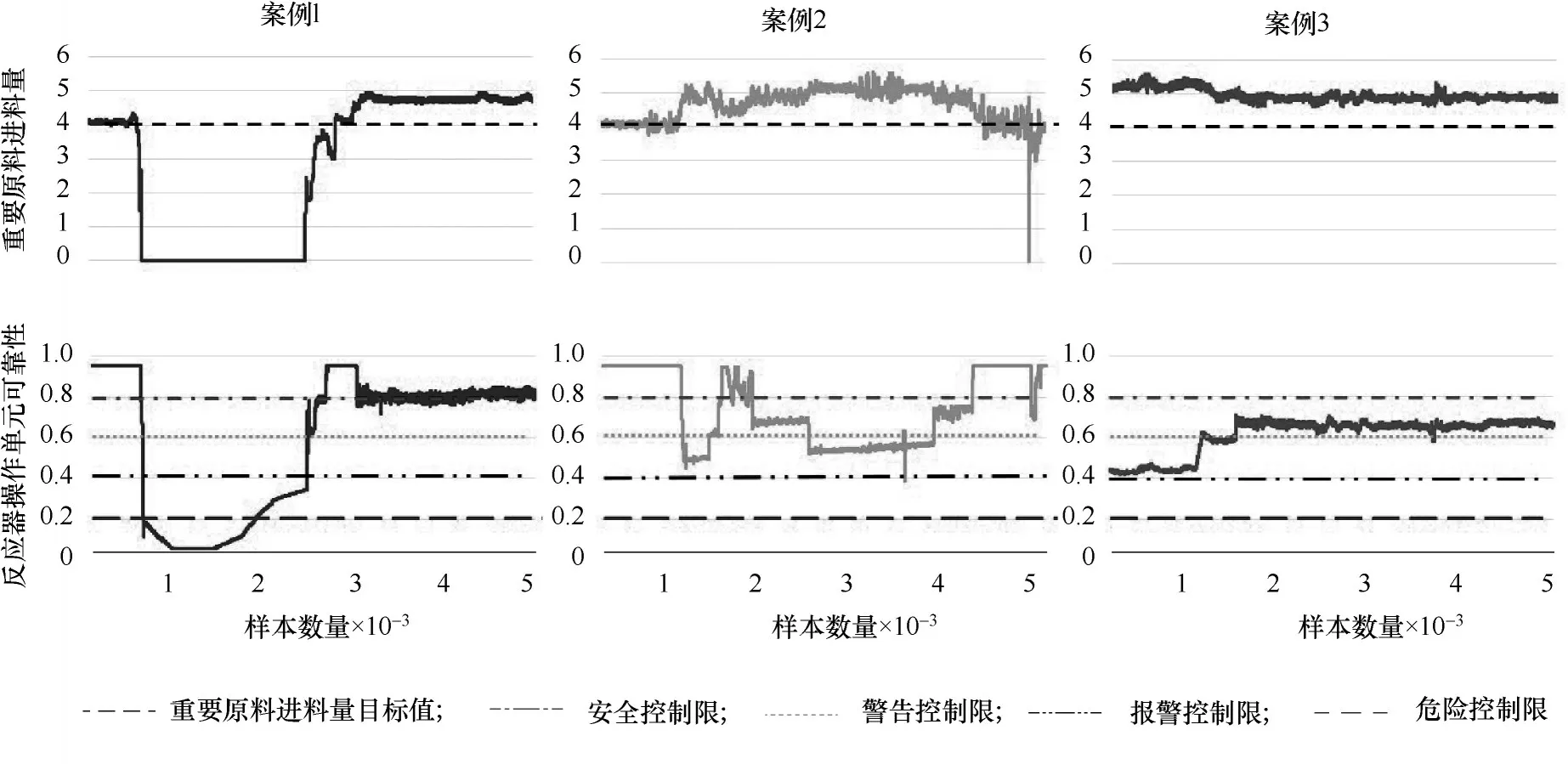
圖5 R-22重要原料進料量和反應器操作單元可靠性的3個案例Fig.5 Three cases of R-22's important raw material feed volume and reactor operating unit reliability

在案例2中，隨著重要原料偏離其目標值，反應器操作單元可靠性也隨之下降且處于警告控制限（60%）附近，隨后重要原料逐步恢復到目標值附近，反應器操作單元可靠性也逐漸恢復到90%以上，在案例2 的末期，重要原料的進料量有短暫大幅下降的階段，此階段的反應器操作單元可靠性也及時做出了預測。

在案例3 中，重要原料的進料量在高于其目標值的位置維持基本穩定，此時的反應器操作單元可靠性也處于安全控制限和警告控制限之間，且當重要原料進料量高于5 時，反應器操作單元可靠性會下降到警告控制限以下，說明反應器操作單元可靠性對重要原料進料量的波動是敏感的。

由于已有的研究中缺少成熟的操作單元可靠性評估方法與本文提出的方法進行對比，因此為了驗證提出的方法的優越性，在不同專家知識的指導下設計了模糊推理系統估計反應器操作單元的可靠性，并與GLSAFIS 的估計結果對比，圖6是上述三個案例在GLSAFIS 方法以及2位專家指導下反應器操作單元可靠性估計的結果。可以發現，雖然專家知識得到的可靠性估計結果與GLSAFIS 方法的結果保持大致相同的趨勢，但是整合專家知識估計的可靠性與反應器單元實際情況有較大區別。例如案例1，初期反應器正常平穩運行，整合專家知識評估的可靠性卻在70%以下，隨后重要原料進料量降為0，反應器可靠性應當迅速降低，此時整合專家知識評估的可靠性仍保持在50%；案例2中整合專家2知識的可靠性估計值明顯低于實際情況；案例3 中整合專家1 知識對反應器可靠性的波動不敏感，維持在60%附近。而且不同專家知識得到的結果也有較大差異，通過將全局和局部特征代替專家知識選擇過程變量作為模糊推理系統的輸入，不僅克服了對專家知識的依賴，而且避免了不同專家知識偏差帶來的結果上的誤差。

圖6 R-22反應器操作單元可靠性估計結果對比Fig.6 Comparison of reliability estimation results of R-22 reactor operating unit

更為重要的是，如果采用常規FIS，需要設計310=59049個模糊規則，其設計復雜度已經遠遠超出了工業過程的實際應用的可行性。而采用GLSAFIS模型，僅需設計33=27 個模糊規則。系統設計的工作量大大降低，工作效率和可維護性等均顯著提高。

2.2 TE模型反應器操作單元可靠性估計

為了進一步驗證所提方法的泛化性能，在TE模型中也進行了應用。田納西伊斯曼過程（Teenesse Eastman process，TEP），簡稱TE 過程，是由Downs 和Vogel[29]于1993 年提出的美國田納西伊斯曼化學品公司的實際化工過程的計算機模擬，此后Bathel等[30]對模擬程序進一步優化，增加了新的故障和更多的監測變量。TE 過程逐漸發展成為檢測過程控制技術和過程監測方法性能的一個基準化工模擬過程[31]。如圖7 給出了TE 過程流程圖，該過程包含5 個操作單元：反應器，冷凝器，分離器，汽提塔和壓縮機。TE 過程包括6 種操作模式，每種操作模式下產物G、H 的比例不同。在模擬過程中可以對TE 過程設置故障，TE 過程目前可以設定的故障有28 個。具體細節可參考文獻[29-30]。

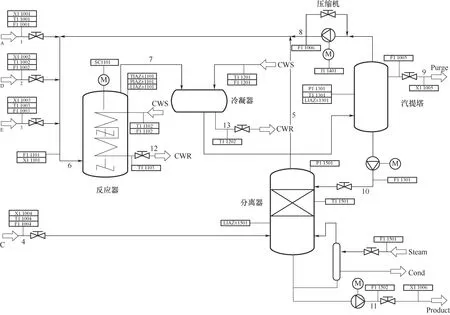
圖7 TE過程流程圖Fig.7 Flow chart of TE process

以TE 模型的反應器和分離器操作單元為例介紹應用的具體過程及結果。TE 模型有22 個在線測量的過程變量和12 個操作變量。依據上文介紹的變量選取方法，反應器單元過程變量為過程變量1、2、3、5、6、7、8、9、20、21 以及操作變量1、2、3、4、10、12。分離器操作單元過程變量為10、11、12、13、14以及操作變量6、7。將正常運行期間的1441個數據樣本作為訓練集，整理出各操作單元變量所對應的過程數據并分別訓練GLSA 模型，分別保留前三個最大的特征值。將投影變量作為輸入，操作單元可靠性作為輸出設計模糊推理系統，依據1.2 節中介紹的相關設計方法和原則設計模糊推理系統。圖8(a)、(b)分別是TE 反應器和分離器操作單元輸入和輸出變量的隸屬度函數。

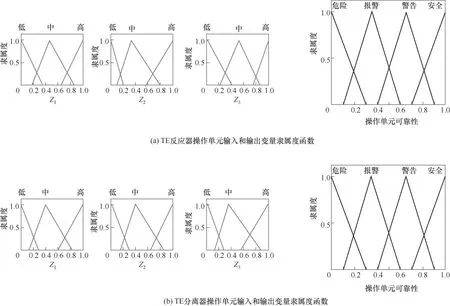
圖8 TE反應器和分離器操作單元的隸屬度函數Fig.8 Membership function of TE reactor and separator operating unit

值得注意的是，采用常規FIS，TE反應器單元可靠性評估需要316=4.30×107個模糊規則，TE 分離器操作單元需要設計37=2187 個模糊規則，而采用GLSAFIS 算法，僅需設計27 個模糊規則。無論是初期的算法設計還是后期的維護，GLSAFIS 算法在實用性方面具有明顯優勢。

在TE 過程中引入故障并應用提出的方法估算反應器和分離器操作單元的可靠性，結果顯示：當操作單元發生故障時，操作單元可靠性會出現明顯的下降。當故障發生在其他操作單元時，該操作單元可靠性不會發生明顯的變化。圖9 列舉了3 種典型故障下的反應器及分離器操作單元可靠性的變化。

案例1 是引入故障1（A/C 進料比，4 號管線）后的反應器和汽提塔操作單元可靠性的情況。可以看到：反應器操作單元可靠性維持在安全控制限以下而汽提塔操作單元可靠性維持了一段高水平后迅速下降。故障1 是分離器進料管線上發生的故障，說明提出的方法可以準確反應操作單元的狀態。

案例2 是引入故障6（A 進料損失，1 號管線）后的反應器以及汽提塔操作單元可靠性的變化情況。在引入故障6 后，反應器操作單元可靠性迅速下降到危險控制限以下，說明A 進料損失造成了反應器可靠性的嚴重降低。事實上，在引入故障6后，仿真程序將在6.2 h后關閉，這也有力地證明了該故障造成的嚴重損害，同時也證明了本文提出方法的較優性能。

案例3是引入故障15（冷凝器冷卻水調節閥）后反應器和汽提塔操作單元可靠性的變化。雖然有故障的引入，但是由于故障發生在冷凝器，所以反應器和分離器操作單元可靠性一直維持在很高的水平。表明提出的方法對操作單元可靠性的估計是準確的。

3 結 論

提出了GLSAFIS 方法在線評估氟化工生產過程操作單元可靠性，并在模擬化工過程程序中進行了應用。在選取操作單元過程變量后通過全局-局部結構分析算法對操作單元過程變量進行降維，根據模糊推理得到操作單元可靠性的指標，可以實時監測操作單元的運行狀態。提供適宜的維護建議，確保氟化工生產過程的安全運行。所提出的方法的重要特點是不依賴專家知識，具備很強的可推廣性。本文在研究中考慮了過程變量對于操作單元可靠性的影響，在將來的研究中可以融合環境、人員等多要素來評估操作單元的可靠性。對于操作單元可靠性的預測也是未來的研究方向之一。