水-植物隨機模型正解全局存在性與持久性

王晶囡, 陳 輝, 楊德中, 陸超軼, 譚雨麗

(哈爾濱理工大學理學院，哈爾濱 150080)

1 引言

內(nèi)蒙古東部的科爾沁沙地，陜西省榆林市的毛烏素沙地，新疆南部的塔里木盆地是我國最嚴重的三大荒漠化地區(qū).近年來，我國對內(nèi)陸盆地荒漠化問題，采取了一系列重大舉措加強防沙治沙工作，盡管全國范圍內(nèi)荒漠化土地從上世紀末年均擴展1.04 萬平方公里轉(zhuǎn)變?yōu)槟壳澳昃s減0.2424 萬平方公里.但目前我國土壤荒漠化的面積仍有261.16 萬平方公里，占國土面積的27.2%.本文是以“探討水與植物可持久生存的條件，為治理科爾沁等地區(qū)的荒漠化問題提供理論依據(jù)”為出發(fā)點而進行研究.大量的研究證實，科爾沁等土壤荒漠化地區(qū)斑圖的形成條件是多方面的，主要包括土壤條件、氣候條件、地貌條件、水文條件、植被條件以及人為因素.文獻[1]提出了如下的水-植物相互作用的數(shù)學模型

2 水-植物隨機模型解的有界性

其中H(b) = 1，意味著在荒漠化地區(qū)，植物對于水的需求很強，對水的競爭十分激烈，無論植物的密度較低還是較高，植物與水不會有化學反應，植物會將水分完全吸收.

另外，針對地勢分布均勻的荒漠化地區(qū)水與植物相互作用的特點，本文在建模時忽略了模型(1)中擴散性和坡度問題，采用機制(2)的形式來描述荒漠化地區(qū)植物與水作用的機理，用x(t)和y(t)分別表示水和植物的量，可得到如下模型

另外，對于補水的量來說，補給水的供給形式、供給時間和供給地點都不會對它產(chǎn)生影響，只有供給量會產(chǎn)生影響，而供水量的隨機影響相對隨機補給對植物增長量的隨機影響很小，所以本文的模型更著重探討隨機補給對植物增長量的隨機影響，忽略補給水量的隨機影響，我們在模型(3)中引入了如下形式的隨機項(高斯白噪聲)

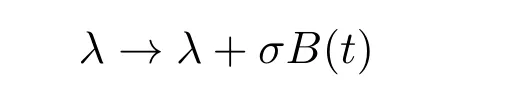
來刻畫隨機補給水的供給形式、供給時間、供給地點以及供給量對植物生長的隨機影響，其中B(t)是B(0) = 0 的標準一維布朗運動，σ ＞0 為隨機強度.從而，得到如下具有隨機效應的水-植物模型

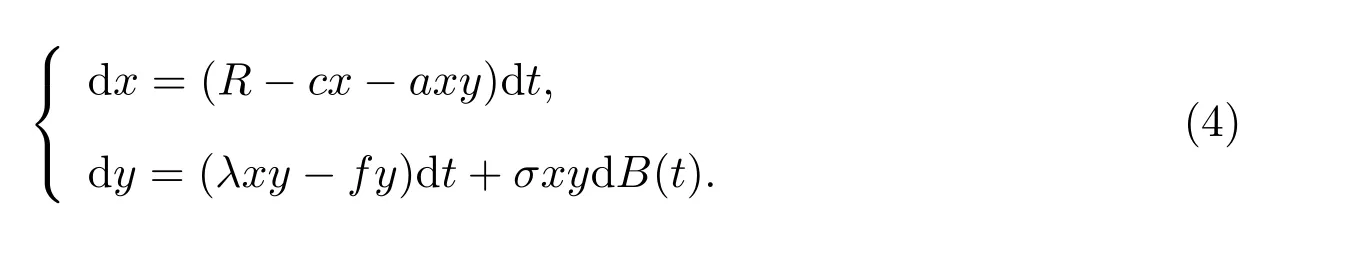
為了便于研究水-植物隨機模型的動力學性質(zhì)，參考了文獻[5-9]的研究方法，若除非特殊聲明，否則本文所有的隨機變量和隨機過程均定義在一個帶σ域流的概率空間(Ω,F,Ft,P)上，其中Ft={Ft}t∈[0,+∞)滿足通常條件(詳見文獻[6])，并給出如下定義、符號和公式：

1) 定義

則物種x(t)稱為是強平均持久；

3) 多維公式[6].如果X(t)是滿足隨機方程dX(t) = f(t)dt+g(t)dB(t)的一個多維It?o 過程，其中f(t)∈L1(R+,Rd),g(t)∈L2(R+,Rd×m).令V(X(t),t)∈C2,1(Rd×R+,R)，那么V(X(t),t)也是一個It?o 過程，且滿足

對式(5)兩邊從0 到t積分，可得

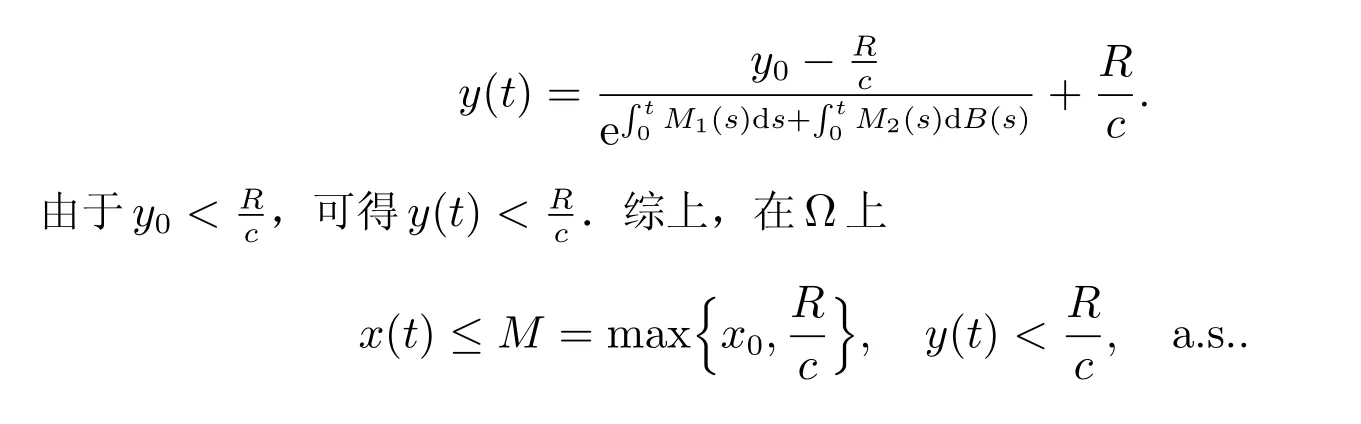
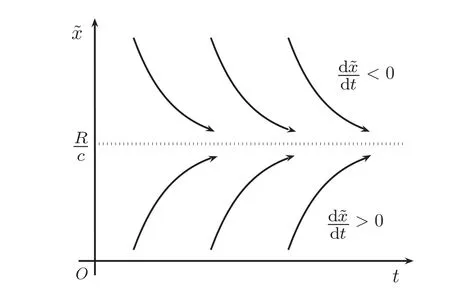
圖1 x(t)的軌道波形示意圖

3 水-植物隨機模型的持久性分析

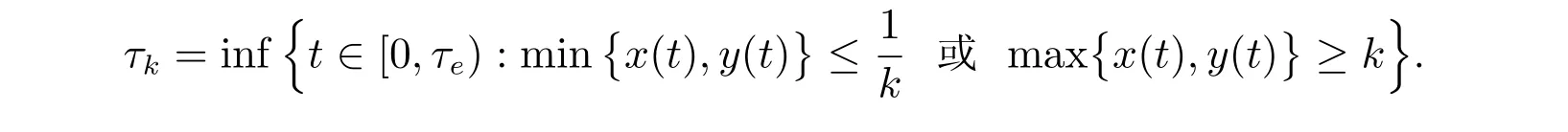
顯然，當k →∞，τk是遞增的，令τ∞= limk→∞τk，由幾乎處處τ∞≤τe可知，若τ∞達到∞，則τe達到∞，模型就存在唯一的全局正解.下面用反證法[7,8]證明τ∞達到∞.假設τ∞不能達到∞，則存在常數(shù)T ＞0 和ε ∈(0,1)，使得P {τ∞≤T} ＞ε成立.因此，存在整數(shù)k1，使得

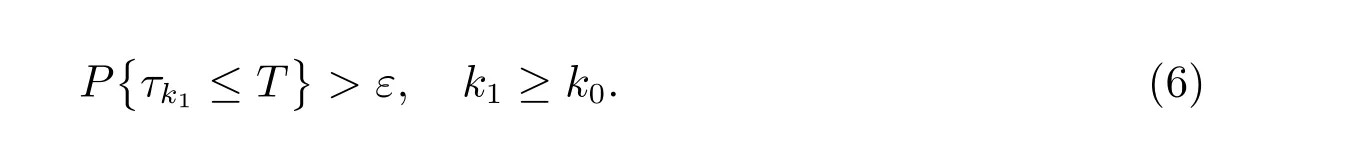
由引理1 可知，模型(4)的解有界，因而可得

這里I(Ωk)是Ωk的示性函數(shù).一方面由V(x0,y0)有界，可以得到V(x0, y0)+LT ＜∞；另一方面當k →∞時，ε[2(k-1-lnk)∧2(1/k-1+lnk)∧(k+1/k-2)]趨向無窮，由此可得V(x0,y0)+LT趨向無窮.于是有∞=V(x0,y0)+LT ＜∞，推出矛盾，所以假設τ∞取不到∞，是不成立的，即τ∞可達到∞，這就證明了模型存在唯一的全局正解，定理得證.

綜上，植物是強平均持久的，定理得證.

4 數(shù)值模擬

下面利用數(shù)值模擬展示模型(3)與隨機模型(4)中植物與水的演化過程圖.基于荒漠化地區(qū)干燥的特點，水的蒸發(fā)率c和植物的死亡率f，植物的吸收率a都應該偏大，而植物吸收水后的增長率λ要比植物的吸收率a小.由理論分析結(jié)果，現(xiàn)取參數(shù)條件為

取隨機強度分別為σ= 0.01, σ= 0.08 和σ= 0.15 進行數(shù)值模擬，模擬結(jié)果如圖2 和圖3 所示.

圖2 隨機強度較小時，模型(3)和模型(4)中水與植物的軌道波形圖

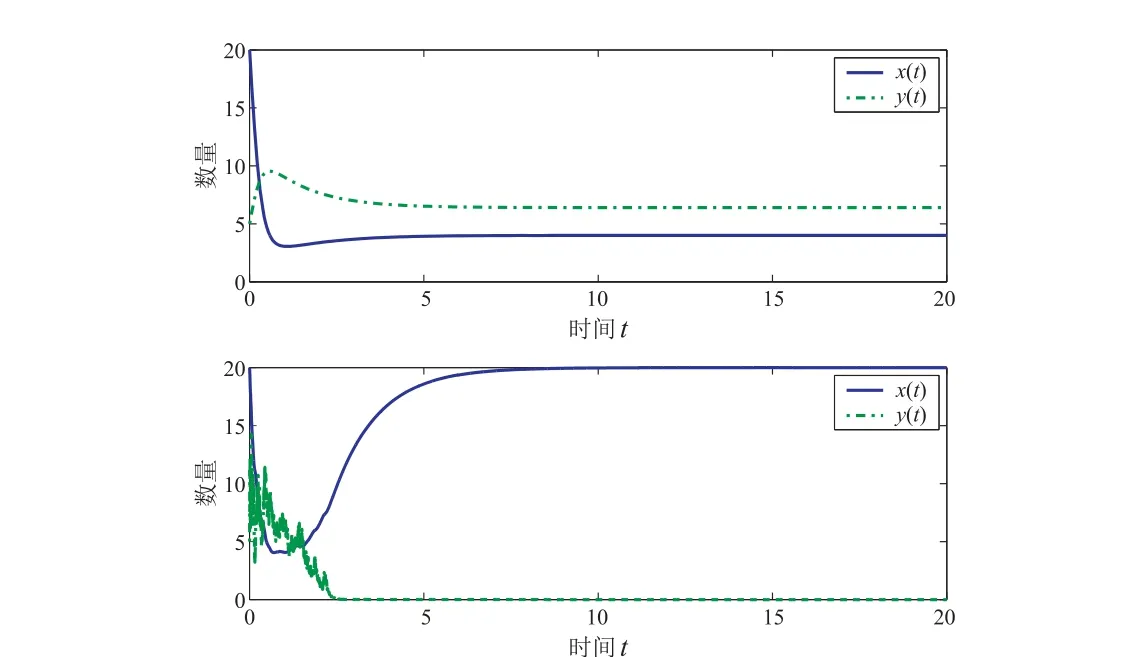
圖3 隨機強度σ =0.15 較大時，模型(3)和模型(4)中水與植物的軌道波形圖

在圖2 和圖3 中，位于上面的波形圖模擬了模型(3)中水與植物波形圖，位于下面的波形圖模擬了具有隨機效應模型(4)中水與植物波形圖.圖2 中展示了，模型(3)在無隨機干擾時，水和植物處于持久共存狀態(tài)，此時受到較小環(huán)境噪聲干擾后，水與植物仍然能處于持久共存狀態(tài).這是因為隨機強度σ= 0.01 和σ= 0.08，均處于植物強平均持久的參數(shù)范圍σ2＜0.016 內(nèi).但不同的隨機強度對植物生長的隨機影響略有不同，隨機強度較大者σ= 0.08 對植物生長的隨機影響相對隨機強度σ= 0.01 較大.圖3 展示了，隨機強度σ= 0.15 在植物的強平均持久的參數(shù)范圍之外時，即σ2＞0.0165，此時植物在短時間內(nèi)受到巨劇烈隨機干擾后，快速趨于滅絕.通過對比圖2 和圖3 可知，水補給的隨機強度過大，會導致植物的滅絕；如果環(huán)境中水補給隨機強度較小，不會導致水和植物的最終滅絕，植物會以不同的形式存在，如斑圖[1]等形式.

根據(jù)理論和數(shù)值模擬的結(jié)果可知，要想讓植物存活于荒漠中，就要為其創(chuàng)造如下條件，以供植物的生長：

1) 調(diào)節(jié)水補給的隨機強度以減少環(huán)境隨機變化對荒漠化地區(qū)植物生長的影響；

2) 在荒漠化地區(qū)種植適應環(huán)境的植被，以減少植物的死亡率，從而達到的植物與水的共存；

3) 要定期增加水的供給，如飼養(yǎng)畜牧，人工灌溉，使用固體水等保水劑，使植物具有充足的水分；

4) 減少水分的蒸發(fā)，如采用集水帳篷等.

5 結(jié)論

本文討論了具有隨機效應的水-植物模型的正解全局存性和持久性問題.通過研究具有高斯白噪聲隨機波動因素的水-植物模型，利用相圖分析法、It?o 公式、平均積分法和局部鞅的強大數(shù)定律，推出了水-植物隨機模型解的有界性、證明了該模型的正解全局存在唯一性，得到了水-植物隨機模型的強平均持久的充分條件.從而獲悉水補給隨機性對植物增長的影響規(guī)律：補給水的隨機強度適中會改善植被的增長；補給水的隨機強度較小可能出現(xiàn)斑圖現(xiàn)象；補給水的隨機強度過大會導致植物的滅絕，不利于植物生長.這些研究結(jié)果為治理土地荒漠化提供了理論依據(jù).