具有非局部捕食效應的藻類-貽貝系統空間分布模式研究

李 靜 孫桂全

(1. 山西財經大學應用數學學院，太原 030006; 2. 中北大學理學院，太原 030051;3. 山西大學復雜系統研究所，太原 030006)

1 引言

海岸帶作為連接陸地與海洋的過渡帶，具有豐富的生物資源、景觀資源和空間資源等，是我國人口最為稠密、社會經濟最為活躍的地區譬如珠江三角洲、長江三角洲和粵港澳大灣區.海岸帶生態系統作為沿海經濟帶最重要的生態安全屏障，在當前經濟迅速發展和人為活動日益頻繁等多重影響下，其生態結構和功能遭受了前所未有的威脅和挑戰，因而對海岸帶生態系統的研究變得更加迫切.貽貝作為海岸潮間帶區域的常見種，大量的種群棲息在不同的海岸潮帶地區，形成了尺度大約在1 米到100 米之間具有規律的空間分布結構，這些貽貝不僅是食物鏈網絡的重要環節，而且也為人類供給了豐富的食物資源.因此，研究這類種群的空間分布結構對維護海岸生態系統的物種多樣性起著關鍵作用.van de Koppel 等人[1]表明在外界環境的擾動下，生物種群在空間上的異質分布結構具有比同質分布結構更強的抵抗力和恢復力.因此，研究影響貽貝空間分布模式的因素能夠為維護海岸生態系統的可持續發展提供一些建議和理論依據.

為了研究貽貝種群空間分布模式的演化規律，生物和數學方面的科研工作者已開展了相關研究內容.van de Koppel 等人[1]根據藻類的生長規律以及藻類與貽貝之間的捕食關系，首次提出了一個反應擴散對流模型來刻畫瓦登海海岸上貽貝規則空間分布模式的自組織演化過程.Wang 等人[2]呈現了空間分布模式形成的詳細數學分析，發現空間分布模式是非線性項作用的結果，而且具有不同波長，振幅和運動速度的多種尺度空間模式可能共存.Liu 等人[3]通過構建了一個包含貽貝、藻類和軟沉積物的三變量反應擴散對流模型去分析自然界中貽貝聚集形成的空間分布模式，表明了個體行為聚集形成的小尺度網狀格局和貽貝之間捕食促進與資源枯竭相互作用形成的大尺度帶狀空間結構提高了貽貝生態系統的復原力.Cangelosi 等人[4]利用弱非線性擴散不穩定方法研究了藻類-貽貝模型發生Turing 失穩的條件，并從數值仿真的角度展示了對應的空間分布結構.Song 等人[5]采用反應擴散方程的規范型理論研究了不考慮對流項的藻類-貽貝模型產生余維二的Turing-Hopf 分支的條件以及給出了更準確的Turing-Hopf 分支點附近動力學區域的劃分，進一步證明了Turing-Hopf 的相互作用顯著增強貽貝空間分布模式的多樣性.Shen 和Wei[6]通過在藻類-貽貝模型中引入時滯效應，研究了在時滯參數的一些范圍內模型能夠產生Hopf 分支，Turing 分支和Hopf-Turing 分支.目前的這些研究工作假設貽貝捕食藻類的過程發生在同一位置的貽貝與藻類之間.事實上，某一位置貽貝生物量的增加是由其它位置的貽貝移動到此處并捕食藻類引起的，這一事實導致了貽貝與藻類的非局部捕食作用.這一過程無法直接用經典的反應擴散方程進行刻畫，因此有必要尋找其他的動力學方程進行描述.而且，這種非局部的捕食作用如何影響貽貝的空間分布模式也待進一步分析求證.

本文主要通過借助非局部時滯反應擴散方程[7,8]來構建動力學模型研究貽貝與藻類之間的非局部捕食作用，并利用Turing 失穩理論研究這種非局部效應對貽貝空間分布模式的影響[9-12]，而關于這類動力學模型的Turing 失穩理論研究尚處于開始階段.本文的內容結構安排如下：第2 節構建了具有非局部捕食效應的藻類-貽貝空間擴散模型；第3 節計算出無擴散系統存在兩個常數平衡點以及分析相應平衡點的局部漸進穩定性，進一步分析擴散系統對應的特征方程根的分布情況，通過三個定理推導出系統發生Turing 失穩的條件.第4 節，通過數值模擬呈現出貽貝空間分布模式隨時間的演化規律并最終形成高密度的點狀空間分布結構，進一步通過參數敏感性分析方法研究了影響貽貝空間分布模式的因素；第5 節對全文進行總結和討論.

2 模型

其中A(x,t)表示t時刻x位置的潮水邊界層海藻的濃度，M(x,t)表示t時刻x位置貽貝種群的密度，其他的參數描述見表1.

表1 模型參數說明

事實上，由鞭毛運動的游動機制引起的主動橫向擴散加上其在上下水層的垂直擴散組成了藻類的隨機擴散，故在上述模型(1)的第一個方程中引入DA?2A，其中DA描述藻類的擴散系數.為了更深刻地理解兩種群的隨機擴散對藻類和貽貝系統相互作用的影響，在這塊忽略藻類的對流項，即假設V=0.考慮到貽貝能夠隨著潮水流動進行隨機擴散并且擴散需要時間完成，t-s時刻在y位置的貽貝經過了s段時間在t時刻到達x位置并捕食此位置的藻類引起了t時刻x位置貽貝種群生物量的增加.為了建模這種非局部捕食情形，我們將在模型(1)的貽貝方程中引入時空卷積算子

進行表示，構建了如下具有非局部捕食效應的藻類-貽貝空間擴散模型

其中(x,t)∈R2×(-∞,+∞)，M(y,s)表示s時刻y位置貽貝的密度，核函數G(x,t)是可積函數，假設有如下形式

G(x-y,t-s)表示t-s時刻y位置的貽貝密度對t時刻x位置貽貝種群的影響大小，且從y位置移動到x位置所需要的時間是s.

由于上述系統(2)對應的特征方程不易求解，故直接利用Turing 失穩理論分析系統(2)是比較困難的.根據Yang 和Xu[15]的方法，通過令P(x,t) = (G*M)(x,t)，則系統(2)被轉化為如下的三變量反應擴散系統

3 動力學分析

3.1 局部穩定性分析

當不考慮貽貝和藻類的擴散時，系統(4)變成如下的常微分系統

成立，則貽貝滅絕平衡點E0是穩定的.否則，貽貝滅絕平衡點E0是不穩定的.

進一步，通過求解可獲得系統(5)在貽貝生存平衡點E*處的雅克比矩陣為

這里

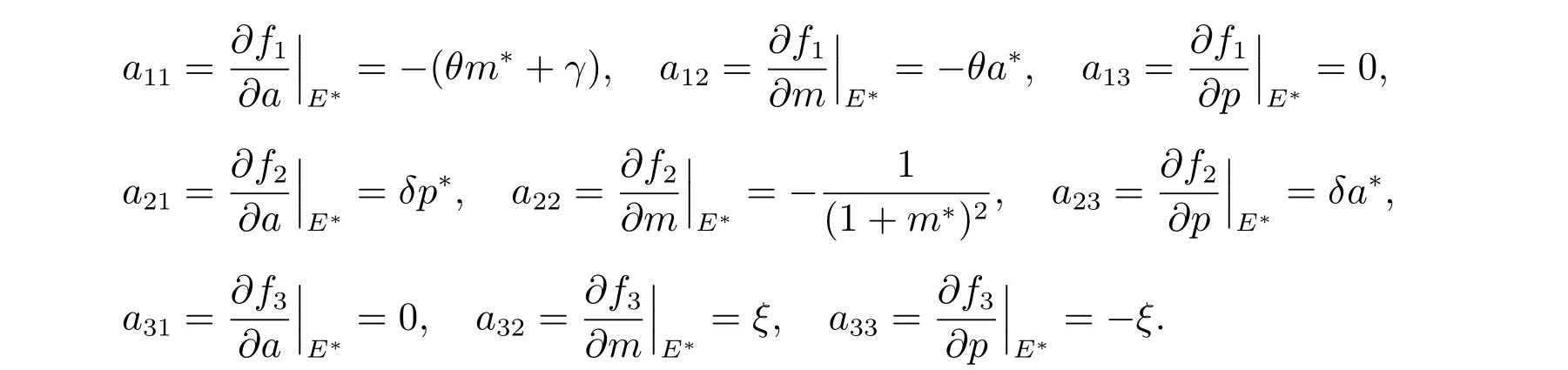
同時可推導出對應的特征方程為

若條件(H0)成立，顯然有a0＞0.同時設Δ1=a2a1-a0，且記Δ1=A2θ2+A1θ+A0，其中

成立，則得到A0＞0，顯然可推出Δ1＞0.根據Routh-Hurwitz 判據[16]，即當特征方程(8)對應的系數a2＞0, a0＞0 和Δ1＞0 時，其所有特征值的實部都是負的，從而表明E*是局部漸進穩定的.

圖1 系統(5)的參數分岔圖(γ =0.554, ξ =0.8)

3.2 Turing 失穩分析

對于海岸帶上的貽貝生態系統，人們主要關注貽貝的持續生存狀況以及在潮間帶上的空間分布模式等信息，所以我們將研究系統(4)在貽貝生存平衡點E*處的Turing 失穩理論，給出空間分布模式存在的條件.根據3.1 部分的分析，可知E*滿足方程組f1(a*,m*,p*) = 0, f2(a*,m*,p*) = 0 和f3(a*,m*,p*) = 0.對系統(4)在E*處進行泰勒級數展開并忽略高階非線性項，可獲得如下的線性系統

進一步，通過對E*=(a*,m*,p*)作非均勻時空微擾，則可令[10]

通過對特征方程(12)的系數進行分析，發現對任意的k ＞0，由于a2＞0 成立，都有b2(k)＞0，但b0(k), b1(k)和T(k)的符號大小不確定.接下來將討論系統(4)發生Turing 失穩的條件，進而分析貽貝的空間分布模式.

定理1 如果條件(H0)和(H3)成立，同時下列條件

都成立，則存在k ＞0，使得系統(4)的貽貝生存平衡點E*變得不穩定.

證明 通過對系統(4)在貽貝生存平衡點E*處進行時空線性化，可推導出相應的特征方程(12)，且對于任意的k ＞0，都有b2(k)＞0.考慮到b0(k)的符號不確定，設置K=k2，則

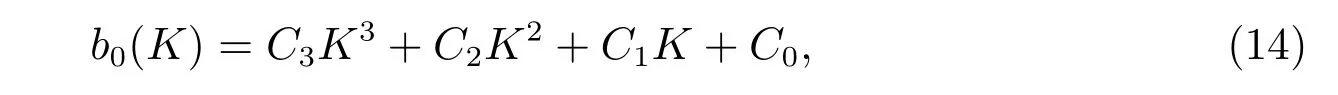
其中

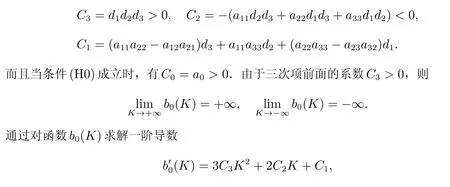
如果條件(C1)成立，有K2＞0＞K1.如果條件(C2)成立，可獲得極小值b0(K2)＜0，并結合b0(0) =a0＞0，這表明了存在k ＞0，使得b0(k)＜0，見圖2.根據Routh-Hurwitz 判據[16]，可知系統(4)的貽貝生存平衡點E*變得不穩定.

圖2 三次函數b0(K)隨著K 變化的示意圖

定理2 如果條件(H0)和(H3)成立，同時下列條件

都成立，則存在k ＞0，使得系統(4)的貽貝生存平衡點E*變得不穩定.

證明過程與定理1 的證明過程一致，此處不再詳細敘述.

定理3 如果條件(H0)和(H3)成立，同時下列條件

都成立，則存在k ＞0，使得系統(4)的貽貝生存平衡點E*變得不穩定.

證明 對于系統(4)對應的特征方程(12)，T(k)的符號大小不確定.通過設置K=k2，T可寫成下面的形式

如果條件(D1)和(D2)成立，可推導出K2＞K1＞0.進一步，根據這兩個極值點在T′′(K)的符號，即

如果條件(D3)成立，可獲得極小值T(K2)＜0，并結合T(0)＞0，這表明了存在k ＞0，使得T(k)＜0，見圖3.根據Routh-Hurwitz 判據[16]，可知系統(4)的貽貝生存平衡點E*變得不穩定.

圖3 三次函數T(K)隨著K 變化的示意圖

英國學者Turing[9]于1952 年首次提出Turing 失穩和空間分布模式的概念，并從數學的角度去理解這個概念，即無擴散系統(常微分方程系統)的平衡點是局部漸進穩定的，而對應的這個常值平衡點在擴散系統中失去穩定性，并隨時間在空間中進行自發的演化，最終形成具有規律的空間分布模式，稱這一過程為Turing 失穩.

進而，根據定理1 至定理3，系統(4)發生Turing 失穩的條件被總結如下

(16)式中的3 個關系式只要有一個成立，系統(4)就會發生Turing 失穩，所以圖4 給出了在不同參數值變化下，特征方程(12)的系數b0(k2)和T(k2)與波數的平方k2的關系.在前述部分已經分析出對任意的k都有b2(k)＞0 成立，故在此處無需展示b2(k2).圖4(a)顯示了b0(k2)＜0 的范圍隨著非局部捕食效應ξ或者藻類擴散率d1的增加而逐漸擴大，而b0(k2)＜0 只在貽貝對藻類消耗率θ= 1.0 時才成立，這表明了非局部捕食效應和藻類擴散率的變化更利于系統發生Turing 失穩，進而維持貽貝的空間分布模式.由圖4(d)至圖4(f)可以看出，對所有的k2＞0 都有T(k2)＞0 成立，說明了由于T(k)的表達式比較復雜，滿足第二和三個關系式發生Turing 失穩的參數比較難尋找但理論上是存在的.

圖4 特征方程(12)的系數b0(k2), T(k2)隨k2 的變化情況

4 主要結果

為了直觀的展示貽貝的空間分布模式，我們將利用向前差分格式對系統(4)進行數值模擬.具體步驟是先對時間進行離散化，設置時間步長Δt=0.005；再通過網格剖分的方式把二維空間區域均勻地劃分成M×M個格子，其中二維空間長度和格子單元長度分別設置為Lx=Ly= 100 和Δx= Δy= 1；最后，利用向前差分格式在離散空間區域上求解系統(4).在數值模擬過程中，貽貝的空間分布結構不再隨時間演化表示模擬結束.在接下來的數值模擬結果中，圖片中豎條棒上的刻度代表貽貝在某個空間位置上的密度，豎條棒上顏色的深淺代表密度的增減.

4.1 空間分布模式

當參數取γ=0.554, θ=1.1, ξ=0.8, δ=1.40, d1=1.2, d2=0.04, d3=0.02 時，圖5(a)至圖5(d)呈現了貽貝在空間上的分布隨時間演化的過程，其中圖5(d)代表最終形成的空間分布模式.在初始時刻，貽貝種群均勻地分布在空間中，隨著時間的推移貽貝種群在空間中聚集成條狀結構，且少部分位置的密度比較高，隨后貽貝種群逐漸地聚集成許多非常緊密的小群體，最終在空間上形成了高密度點狀分布模式.這一過程直觀的展示了自然界中貽貝在空間中的聚集過程.從圖5(d)中取y= 10, y= 50 和y= 90 平行于x空間方向的3 個位置，圖6 更清楚地展示出在貽貝和藻類的空間分布模式到達固定不變時，貽貝的密度和藻類的濃度在x空間方向上呈振蕩的空間分布模式，進一步發現貽貝和藻類在空間上的分布呈現反相位模式，這是由貽貝與藻類之間的捕食與被捕食關系引起的.當固定x位置時，貽貝和藻類的濃度在y空間方向上也有類似的現象.

圖5 貽貝的空間分布模式隨時間演化的過程

圖6 在y 位置固定的情形下，貽貝的密度和藻類的濃度在x 空間方向上的分布

4.2 參數敏感性分析

為了更清楚的理解貽貝的空間分布模式，需要分析系統(4)中各個參數對貽貝和藻類空間平均密度影響的大小.由于在數值模擬過程中發現參數γ, θ, δ和d3不易使貽貝種群形成空間分布模式，所以這部分不考慮這四個參數的影響.首先，粗略地分析一下非局部捕食效應ξ、藻類的擴散速率d1和貽貝的擴散速率d2對兩個種群空間平均密度的影響，主要采用的方法是在其余參數固定的情形下連續改變某一參數的值導致種群的空間平均密度是否發生變化，若發生變化說明對該參數敏感，否則不敏感.其次，我們將利用Ingalls[17]提出的局部敏感性分析理論來辨識出參數敏感性的程度，這里局部敏感性系數(Slocal)被定義為

其中Par 和Res 分別表示參數和種群的空間平均密度，ΔPar 和ΔRes 分別表示參數和空間平均密度的微小改變量.若Slocal＜0 表示參數值與空間平均密度呈負相關，反之呈正相關.進一步規定[18]：若|Slocal|＜1 表征該參數是低敏感的，若1＜|Slocal|＜2 表征該參數是中等敏感的，否則是高敏感的.

從圖7(a)中觀察到貽貝的空間平均密度隨著參數ξ的增加而變大，而相應的到達空間分布模式不變的時間縮短，這一現象表明了非局部捕食效應促進了貽貝種群的持續增長以及加速了空間分布模式的形成，有利于貽貝種群的持續生存.圖7(b)展示了藻類的空間平均密度呈現了與貽貝種群相反的情形，但到達空間分布模式不變的時間與貽貝種群一致，這是因為貽貝種群在持續增長的同時需要捕食更多的藻類，進而引起藻類的空間平均密度減少.

圖7 對不同ξ 值，貽貝和藻類的空間平均密度隨時間變化的情況

圖8(a)展示了貽貝的空間平均密度隨著參數d1的增加而快速增加，然而藻類的空間平均密度卻逐漸減少，同時兩個種群的密度差急劇變大，產生這一現象的可能原因是藻類種群的擴散加快有助于貽貝捕食到更多的藻類，也就是促進了貽貝種群的增長但反過來抑制了藻類種群的生長，與此同時擴大了二者的密度差.圖8(b)展示了貽貝的空間平均密度隨著參數d2的增加先快速減少之后增加再下降，而藻類的變化趨勢相對比較緩慢并展現了與貽貝相反的情形，同時二者的密度差漸漸縮小之后擴大再縮小，導致這一現象產生的原因可能是貽貝種群的擴散速率增加引起貽貝捕食藻類的能力下降，從而使得更多的藻類得到幸存，但當貽貝種群的擴散率增加到一定程度時，藻類濃度變得更多，使得貽貝捕食藻類變得比較容易，進而引起貽貝的密度增加，之后貽貝密度的增加會導致藻類濃度減少，捕食藻類變得不容易，從而貽貝的密度再次減少，相應的藻類濃度增加.

圖8 貽貝和藻類的空間平均密度隨d1 和d2 變化的情況

由圖9(a)可知，貽貝的空間平均密度與非局部捕食效應ξ和藻類種群的擴散速率d1成正相關，與其自身的擴散速率d2成負相關，且這兩擴散速率參數都為中等敏感參數，非局部捕食效應為低敏感參數.從圖9(b)中可以看出藻類的空間平均密度與貽貝種群的擴散速率成正相關，而與其他兩個參數成負相關，并顯示對這3 個參數都是低敏感的.這一結果表明了兩種群的擴散速率對貽貝的空間分布模式有顯著影響，而非局部捕食效應的影響不顯著，從另一個角度說明了如果人為干擾了貽貝或者藻類的運動規律可能會改變貽貝種群的空間分布模式，進而破壞海岸生態系統的穩健發展.

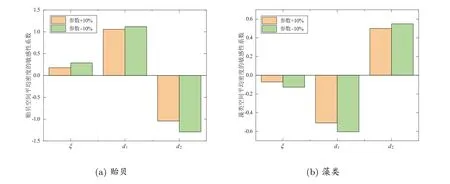
圖9 貽貝和藻類的空間平均密度在參數改變±10%時的參數敏感性分析

5 結論

本文研究了海岸生態系統中貽貝種群空間分布模式的演化規律，基于空間中某一位置貽貝生物量的增加來源于其他位置的貽貝移動到此處并捕食藻類引起的這一自然現象，我們構建了具有非局部捕食效應的藻類-貽貝模型.為了便于分析所構建模型的Turing 失穩理論，通過考慮特殊形式的核函數并令積分項作為新變量就可把模型轉化為三變量反應擴散系統(4).我們計算出無擴散系統存在貽貝滅絕平衡點和貽貝生存平衡點，并給出其局部漸進穩定的條件.進一步，根據Turing 失穩理論推導出擴散系統產生Turing 失穩的條件.然后對模型采用時空離散化和向前差分格式進行數值模擬，展示出貽貝種群的空間分布模式隨時間演化的規律并發現最終形成高密度點狀分布結構.對非局部捕食效應、藻類種群的擴散速率和貽貝種群的擴散速率展開了細致的敏感性分析，結果表明貽貝和藻類種群的擴散速率對貽貝種群的空間分布模式影響較大，而非局部捕食效應的影響不顯著，更利于貽貝生態系統的持續演化發展.這些研究可為海岸生態系統資源的合理開發與維護提供一些理論支撐，同時也豐富了具有非局部效應的反應擴散方程的Turing 失穩理論.