不同坐標系下傅立葉變換性質

李盤潤 劉 瑤

（四川信息職業技術學院，四川 廣元 628000）

傅立葉變換作為一種線性積分變換，在物理學及工程技術有許多應用，通常將時域信號轉變為頻域信號，分析信號的頻域成分。對于簡單的時間信號。通常僅考慮一個維度的信號變化，即一維傅立葉變換。近年來，圖像處理技術越來越多采用傅立葉變換技術，而空間上圖像不再是簡單的一維信號，可以由一維推廣獲得二維傅立葉變換。對于更高維信號，同樣存在高維傅立葉變換。

本文主要針對二維傅立葉變換進行研究。在笛卡爾坐標系下，在空間上對信號做采樣處理，將連續傅立葉變換(CFT)轉換為離散傅立葉變換(DFT)，進而容易在數字計算機上進行計算。而對于某些中心對稱函數，更容易在極坐標上描述，則需要定義在極坐標上傅立葉變換，如傅立葉光學。此時采樣信息為極坐標采樣，因此不能夠采用離散傅立葉的快速算法。而極坐標上采樣可以認為是一種非均勻采樣方法，進而可采用NEFT 實現極坐標采樣條件下的離散傅立葉變換計算。但對于一些特殊的極坐標函數，容易獲得相應連續傅立葉變換的解析解。

本文將針對不同坐標定義下的連續傅立葉變換進行研究，并給出關于連續變換與離散變換及非均勻變換之間的關系。進一步針對某些理想區域上的特殊函數，利用傅立葉變換積分定義，容易計算相應傅立葉變換的原函數。對于特殊的高斯函數，計算其對應的傅立葉變換對。

1 積分變換定義

本節給出不同坐標系條件下，二維傅立葉變換的定義，同時，給出一維Hankel 變換，在后面的內容中，二維極坐標上的傅立葉變換可轉為一維Hankel 變換。

1.1 笛卡爾坐標系傅立葉變換

笛卡爾坐標下，函數f（x，y）在[-∞，+∞]有定義，且滿足傅立葉積分定理條件，則函數：

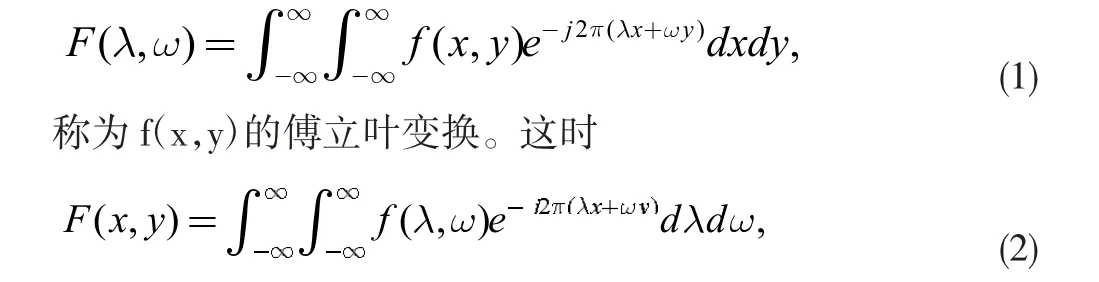
稱為f（λ，ω）的傅立葉逆變換。

f（λ，ω）稱為f（x，y）在傅立葉變換下的象函數，反之，稱為原函數。象函數與原函數構成一組傅立葉變換對。

1.2 極坐標系傅立葉變換

對于某些二維函數，具有中心對稱的性質，相比與笛卡爾坐標系，該函數更容易在極坐標系上描述。在極坐標下，設空間域函數，其對應域上的傅立葉象函數為F（ρ，φ）。則傅立葉變換的形式如下：

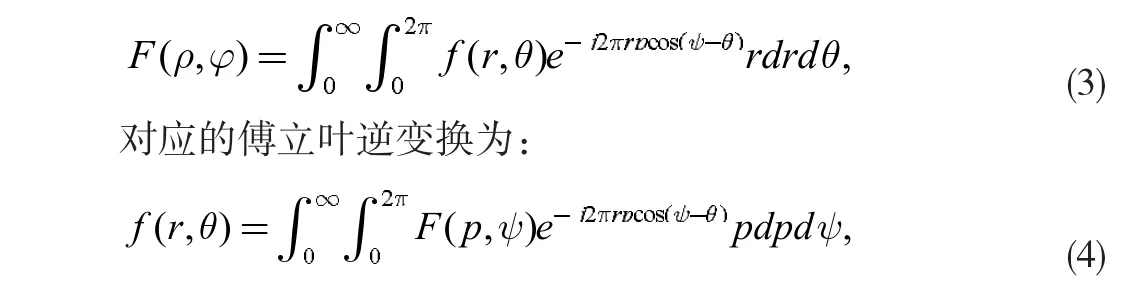
極坐標系的傅立葉變換定義與式(1)與式(2)等價，象函數與原函數構成一組傅立葉變換對。關于兩種定義的等價關系，可通過積分的變量替換方法實現證明，此處不做詳細說明

1.3 Hankel 變換

Hankel 變換為另一類積分變換，n 階Hankel 變換定義為如下積分：

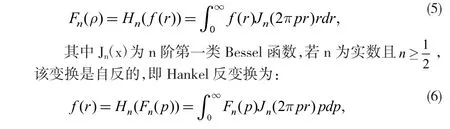
極坐標上的二維傅立葉變換，可通過一維上的Hankel 變換描述，從而容易計算極坐標上的傅立葉變換對。

2 離散傅立葉變換

在笛卡爾坐標系上，式(1)通常為連續傅立葉變換。為使該積分變換的計算能在計算機上進行，需將式(1)連續傅立葉變換轉為離散傅立葉變換。若f（x，y）在x=nT，y=mT（n，m=0，±0，±1，±2，…）是連續的，稱f（nT，mT）為采樣間隔為T 的采樣波形。其對應的離散傅立葉變換為：

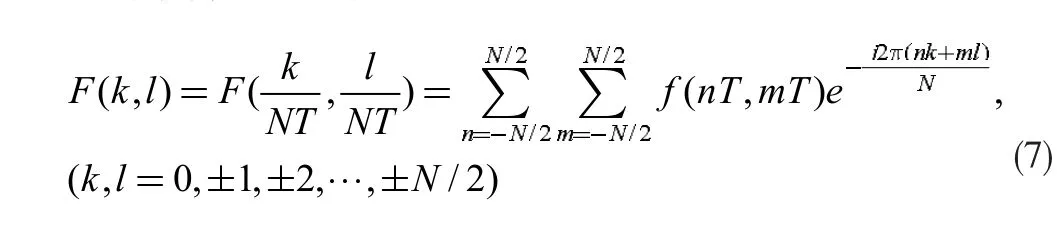
根據采樣定理，頻域上采樣間隔δf=1/NT,關于上式存在快速計算方法(FFT)，需要注意離散傅立葉變換空間采樣及頻域采樣存在極強的耦合關系。

在研究過程中，任意函數關于(1)的連續傅立葉變換不存在耦合關系，但其直接積分計算，需記住黎曼積分計算頻域上特定位置的象函數：

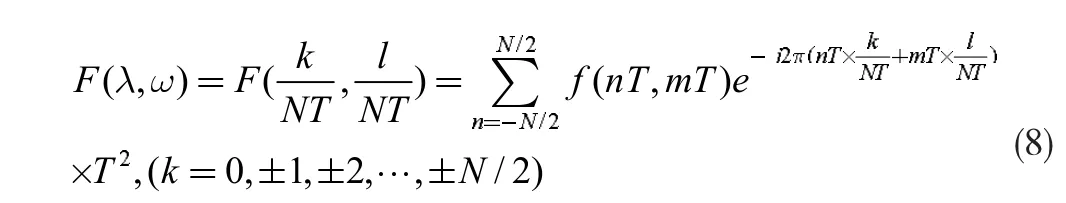
比較(7)與(8)，即連續傅立葉變換與離散傅立葉變換的頻域振幅存在T2的倍數關系，從而可根據快速傅立葉方法（FFT）獲得特定頻域位置上的傅立葉象函數。類似簡單推導可應用在逆變換上。

3 基于采樣的非均勻傅立葉變換

式(7)為離散傅立葉變換，它的快速算法FFT 的計算復雜度為O（nlogn）。但是存在諸多限制，比如頻域點與空間點存在極強的耦合關系δf=1/T，且必須在采樣空間必須均勻采樣。這些限制導致在應用中，如果使用FFT 算法，無法通過在頻率域加密采樣來提高空間域變換結果的精度。連續傅立葉變換，可以避免頻域點與空間點的耦合關系及采樣條件限制，但是需進行復雜且耗時的積分運算。存在基于采樣的非均勻傅立葉變換。

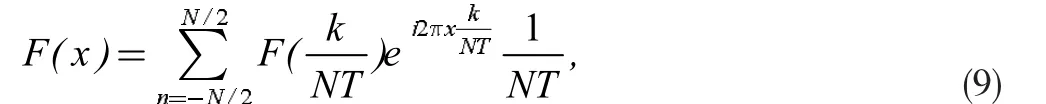
其中x 為空間上任意位置，從而避免的限制，其計算復雜度為O（n2）。對于頻域均勻采樣而空間域非均勻c 采樣的非均勻傅立葉變換，同樣存在快速計算方法[3]。

非均勻傅立葉變換的快速實現。其本質為連續傅立葉變化的離散化。對于離散采樣精度直接影響空間域變換結果的精度，直接的辦法可通過在頻率域加密采樣，提高計算精度。對于某些函數F（p），若采樣結果F（pi）=0。則加密采樣的同時。會增加計算的時間，但對于精度的提升有限。另一種方法是提高頻域采樣精度，取采樣結果為F（pi）采樣對應區域與F（p）有效區域相交面積。該方法等價于在頻率域加密采樣，但僅選擇特殊位置的采樣結果去計算式(9),且該位置的采樣結果為周圍采樣結果的均值。

基于采樣離散傅立葉變換可獲得特定位置(原)象函數值，而非均勻傅立葉變換容易獲得任意位置的（原）象函數值。另一方面，極坐標上的采樣可認為是笛卡爾坐標上的非均勻采樣，從而極坐標上傅立葉變換容易通過非均勻傅立葉變換快速計算。

4 傅立葉變換與Hanker 變換的關系

本節中，著重說明極坐標條件下，連續傅立葉變換可表述為一維Hanker 變換的無窮級數。

4.1 徑向對稱函數

極坐標上某些徑向對稱函數(高斯函數等)，僅需ρ 徑向描述該二維函數，考慮極坐標系下的傅立葉變換定義(3);

對于徑向對稱函數，二維空間上的傅立葉變換，可通過一維的Hankel 變換計算。

4.2 徑向非對稱函數

根據文獻[6]，笛卡爾坐標系的傅立葉變換核存在如下級數展開式：

即傅立葉變換對中，空間函數的級數展開系數fn（r）與對應頻域函數的級數展開系數Fn（ρ）存在倍數關系。

5 理想函數的傅立葉變換

5.1 多邊形區域

若采樣窗口大小為ω 和h，且對應頻域采樣點fn和gm分別為

則對于簡單多邊形區域，順時針定義多邊形區域Ω 的頂點(xi，yi),根據(1)，對應的傅立葉變換：

5.2 圓形區域

針對理想函數，上節對于簡單多邊形區域，給出了笛卡爾坐標系下的傅立葉變換的計算過程。對于更一般的圓形區域，其傅立葉變換更容易在極坐標下的傅立葉變換實現積分計算。

6 結論

本文分別針對兩種坐標系，分別考慮相應的連續傅立葉變換定義。在笛卡爾坐標系條件下，介紹了基于采樣的離散傅立葉變換及非均勻傅立葉變換，通過數學描述與連續變換之間的關系。在極坐標系條件下，二維傅立葉變換容易通過一維上的Hankel 變換快速計算。并分別針對多邊形區域、圓形區域的理想函數，根據傅立葉變換定義，計算相應的(原)象函數。最后，根據Bessel 函數性質，二維高斯函數容易在極坐標系上描述，根據相應傅立葉變換定義，容易獲得空間及頻域上的傅立葉變換對。

致謝:感謝審稿人提出的寶貴修改意見。