關(guān)于粒度重要性公式的改進(jìn)

盧加學(xué)， 汪小燕

（安徽工業(yè)大學(xué) 計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院，安徽 馬鞍山 243032）

1982 年波蘭Pawlak 教授首次提出粗糙集理論[1]，粗糙集理論在處理不確定性、不精確性以及不完全數(shù)據(jù)方面有著巨大優(yōu)勢(shì)，主要的研究內(nèi)容是屬性約簡[2]和規(guī)則提取。 粗糙集理論中的屬性重要度體現(xiàn)的是去掉某個(gè)或某些屬性前后知識(shí)庫分類變化的程度。對(duì)此，許多學(xué)者進(jìn)行了研究。文獻(xiàn)[3-4]給出了基于代數(shù)觀的由屬性依賴度確定屬性重要度的方法。 但屬性依賴度度量在某些情況下處理數(shù)據(jù)存在局限性，從而得不到合理的結(jié)果。文獻(xiàn)[5]提出了包含度理論。文獻(xiàn)[6]結(jié)合信息熵的特點(diǎn)，給出了基于信息觀的條件信息熵的屬性重要度方法。 文獻(xiàn)[7]對(duì)經(jīng)典依賴公式研究，引進(jìn)多數(shù)包含關(guān)系，提出了新的知識(shí)依賴性度量方法。 屬性重要度的確定方法可以為屬性約簡以及屬性權(quán)重問題的研究提供基礎(chǔ)。

然而以上的文獻(xiàn)方法皆是基于單粒度來確定屬性重要度，但在實(shí)際應(yīng)用中多粒度往往起著更重要的作用。多粒度粗糙集[8-9]是一種新型的多視角數(shù)據(jù)分析方法，眾多學(xué)者對(duì)其進(jìn)行了研究。粒度重要性的確定方法也為多粒度粗糙集中屬性約簡以及屬性權(quán)重問題的研究提供了基礎(chǔ)。 孟慧麗等人在文獻(xiàn)[10]中將信息量引入悲觀多粒度粗糙集的下近似分布約簡，定義了粒度的重要度，以粒度的重要度作為啟發(fā)信息設(shè)計(jì)了約簡算法。 但基于等價(jià)關(guān)系的悲觀多粒度的下近似分類條件過于嚴(yán)格，在實(shí)際問題中忽略了一定的誤差允許。文獻(xiàn)[11]將變精度概念引入多粒度，根據(jù)近似質(zhì)量定義變精度的粒度重要度，以此設(shè)計(jì)了約簡算法，但有時(shí)也沒法判斷粒度之間的區(qū)別。 文獻(xiàn)[12]基于近似質(zhì)量定義了內(nèi)外部粒度重要度并結(jié)合三支決策模型可以有效的進(jìn)行粒度的約簡。 文獻(xiàn)[13]從代數(shù)角度定義了變精度多粒度粗糙集，但并未對(duì)粒度重要性進(jìn)行研究。

筆者基于文獻(xiàn)[7]，結(jié)合多粒度粗糙集理論，提出一種新的粒度重要性度量方法，為進(jìn)一步區(qū)分不同粒度的重要性，加入可信系數(shù)計(jì)算粒度的重要性，使得分析結(jié)果更加合理。 最后，通過一個(gè)決策信息系統(tǒng)驗(yàn)證此方法，結(jié)果表明該方法是有效的。

1 粗糙集的相關(guān)理論

定義1[1]設(shè)四元組S=（U，C∪D，V，f）稱為信息系統(tǒng)，其中U 表示對(duì)象的非空有限集合，稱為論域；AT表示屬性的非空有限集合；Va表示屬性a 的值域，V 表示全部對(duì)象在各個(gè)屬性上的取值構(gòu)成的集合；f 表示U×AT→V 的一個(gè)信息函數(shù)，?a∈AT，x∈U，f（x，a）∈Va。

定義2[1]設(shè)S=（U，C∪D，V，f）為信息系統(tǒng)，?A?AT，定義屬性集A 的不可區(qū)分關(guān)系IND（A）為：IND（A）={（x，y）∈U×U|?a∈A，f（x，a）=f（y，a）}，U/IND（A）表示不可區(qū)分關(guān)系IND（A）在U 上導(dǎo)出的劃分，簡記為U/A。 對(duì)?x∈U，[x]A={y|f（y，a）=f（x，a），?a∈A}稱為x 在屬性集A 下的等價(jià)類。

定義3[1]設(shè)S=（U，C∪D，V，f）為信息系統(tǒng)，?A?AT，X?U，X 關(guān)于屬性集A 的下近似集和上近似集分別定義為：A（X）={x∈U:[x]A?X}，A（X）={x∈U:[x]A∩X≠?}。

定義4[7]設(shè)S=（U，C∪D，V，f）為信息系統(tǒng)，?A?AT，X?U，X 關(guān)于屬性集A 的依賴度定義為

這里POSA（X）表示X 的A 正域，也就是X 關(guān)于屬性集A 的下近似集，|·|表示集合的基數(shù)。

定義5[7]設(shè)S=（U，C∪D，V，f）為信息系統(tǒng)，??P?C，??Q?D 給定ρ∈P 依據(jù)依賴度的定義，給出屬性重要度公式

如果sig（ρ，P，Q）=0，則稱ρ 在P 中關(guān)于Q 是不重要的；否則ρ 在P 中關(guān)于Q 是重要的。

2 多粒度粗糙集相關(guān)理論

定義6[10]在多粒度粗糙集中，四元組S=（U，C∪D，V，f）是一個(gè)完備信息系統(tǒng)，其中A1，A2，A3，…，Am?AT。 每個(gè)屬性集稱為一個(gè)粒度，對(duì)U 基于等價(jià)關(guān)系IND（Ai）劃分得到一個(gè)粒度空間，A={A1，A2，A3，…，Am}稱為一個(gè)粒度集。 ?X?U，X 的悲觀多粒度下近似、上近似分別定義為

定義7[12]四元組S=（U，C∪D，V，f）是一個(gè)完備信息系統(tǒng)，A={A1，A2，A3，…，Am}，決策屬性D 導(dǎo)出的劃分為U/D={X1，X2，X3，…，Xs}。 近似質(zhì)量的定義如下

其中，△∈{P，0}表示悲觀和樂觀多粒度粗糙集兩種情況。

定義8[10]四元組S=（U，C∪D，V，f）是一個(gè)完備信息系統(tǒng)，A={A1，A2，A3，…，Am}，決策屬性D 導(dǎo)出的劃分為U/D={Y1，Y2，Y3，…，Yn}，定義悲觀多粒度下粒度集A 的信息量如下

定義9[14]四元組S=（U，C∪D，V，f）是一個(gè)完備信息系統(tǒng)，A={A1，A2，A3，…，Am}，決策屬性D 導(dǎo)出的劃分為U/D={Y1，Y2，Y3，…，Yn}，β∈（0，1]，定義變精度悲觀多粒度下粒度集A 的β 下近似分布粒度熵如下

3 新的近似質(zhì)量及粒度重要性的改進(jìn)

3.1 近似質(zhì)量的改進(jìn)

定義7 中的近似質(zhì)量是依據(jù)悲觀和樂觀下近似計(jì)算的，但基于等價(jià)關(guān)系的分類是精確的，忽略了實(shí)際應(yīng)用中集合一定程度上的包含關(guān)系，這就會(huì)導(dǎo)致出現(xiàn)近似質(zhì)量相同的情況以至于無法區(qū)分兩個(gè)粒度的重要性。為解決該問題，文中提出基于近似質(zhì)量公式、以多數(shù)包含關(guān)系為前提新的知識(shí)依賴性度量公式，使得結(jié)果的分析更加可靠。

例如文獻(xiàn)[15]中的實(shí)例分析，見表1。

表1 風(fēng)險(xiǎn)投資決策信息系統(tǒng)表

其中條件屬性子集族A={A1，A2，A3，A4}={{a1}，{a2}，{a3}，{a4}}，U/D={D1，D2}={{x1，x3，x5，x7，x9}，{x2，x4，x6，x8}}。 依據(jù)近似質(zhì)量公式中的悲觀下近似計(jì)算各個(gè)粒度的依賴度，發(fā)現(xiàn)粒度A1和A3對(duì)于決策分類D2出現(xiàn)A1（D2）與A3（D2）為空集的情況，使得多個(gè)粒度的重要性為0 ，無法直觀的判斷粒度之間的重要性。 出現(xiàn)這種問題的原因是近似質(zhì)量公式有一定的局限性。 為解決此問題，在近似質(zhì)量公式上引入多數(shù)包含度的概念。

定義10[5]（多數(shù)包含度）設(shè)U 是有限非空集合，P（U）表示U 的所有子集構(gòu)成的冪集，對(duì)于?A，B∈P（U），記

則稱D0（B/A）為A 關(guān)于B 的多數(shù)包含度，即B 包含A 的程度。

定義11[7]（相對(duì)錯(cuò)誤分類率） 設(shè)X 和Y 表示有限論域U 的非空子集。 相對(duì)錯(cuò)誤分類率有如下定義

其中D0（Y/X）=|X∩Y|/|X|。

定義12[7]（多數(shù)包含關(guān)系） 令0≤β<0.5，若

成立，則X 與Y 滿足多數(shù)包含關(guān)系。

依據(jù)以上的概念定義新的近似質(zhì)量公式。

定義13 四元組S=（U，C∪D，V，f）是一個(gè)完備信息系統(tǒng)，A={A1，A2，A3，…，Am}為粒度集合，決策屬性D導(dǎo)出的劃分為U/D={Y1，Y2，Y3，…，Yn}。 如果Ai與D 滿足多數(shù)包含關(guān)系，則其定義為

定理1 令四元組S 是一個(gè)完備信息系統(tǒng)，A={A1，A2，A3，…，Am}為粒度集合，決策屬性D 導(dǎo)出的劃分為U/D={Y1，Y2，Y3，…，Yn}。 0≤β<0.5，B?A，則有γ′B（D）≤γ′A（D）。

證明 因?yàn)锽?A，對(duì)于B={A1，A2，…，An}，n≤m，因此

故有γ′B（D）≤γ′A（D）。

定理1 說明隨著多粒度集中的粒度的增加，近似質(zhì)量也隨著增大。

定理2 令四元組S 是一個(gè)完備信息系統(tǒng)，A={A1，A2，A3，…，Am}為粒度集合，決策屬性D 導(dǎo)出的劃分為U/D＝{Y1，Y2，Y3，…，Yn}，且0≤β1≤β2<0.5，則有

證明 定義13 公式中的[1-c（Xi，Yj）]|Xi|可約簡成|Xi∩Yj|，表示的是在參數(shù)β 的條件下兩集合相交的程度，當(dāng)0≤β1≤β2<0.5，如果有c（Xi，Yj）≤β1，則有c（Xi，Yj）≤β2，此時(shí)Xi?β1Yj，則一定有Xi?β2Yj，按照定義13 的

公式則結(jié)論成立。

定理2 說明了在多粒度的框架下，隨著閾值β 的單調(diào)變化，粒度的依賴度也隨之單調(diào)變化。

定理3 令四元組S=（U，C∪D，V，f）是一個(gè)完備信息系統(tǒng)，A={A1，A2，A3，…，Am}為粒度集合，決策屬性D導(dǎo)出的劃分為U/D＝{Y1，Y2，Y3，…，Yn}，當(dāng)β=0 時(shí)，則有

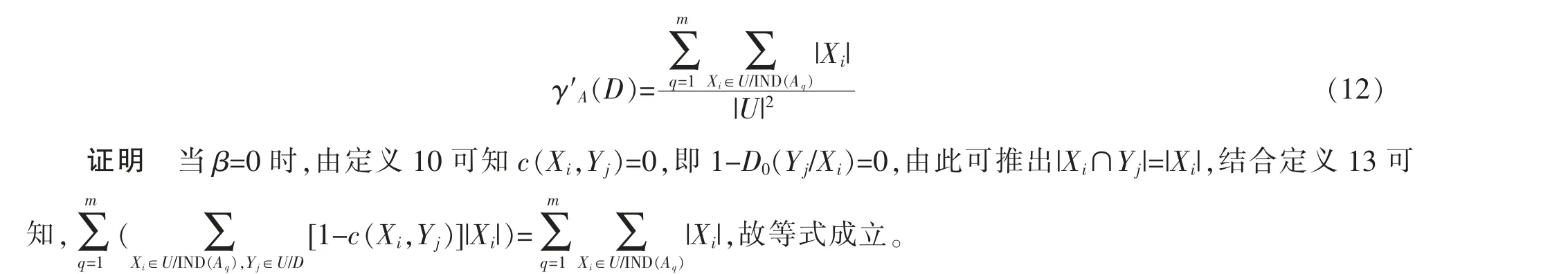
定義14 四元組S=（U，C∪D，V，f）是一個(gè)完備信息系統(tǒng)，Ai∈A={A1，A2，A3，…，Am}，屬性D 導(dǎo)出的劃分為U/D＝{Y1，Y2，Y3，…，Yn}，在粒度集A 上，Ai關(guān)于D 的粒度重要性定義如下i

推論1 四元組S=（U，C∪D，V，f）是一個(gè)完備信息系統(tǒng)，A={A1，A2，A3，…，Am}為粒度集合，決策屬性D導(dǎo)出的劃分為U/D＝{Y1，Y2，Y3，…，Yn}，當(dāng)γ′A（D）=γ′A-{Ai}（D）時(shí)，表明粒度Ai在粒度集A 中關(guān)于D 是不重要的。

定義15 四元組S=（U，C∪D，V，f）是一個(gè)完備信息系統(tǒng)，A′?A={A1，A2，A3，…，Am}，?Ai∈A-A′，定義Ai關(guān)于D 的粒度重要性如下

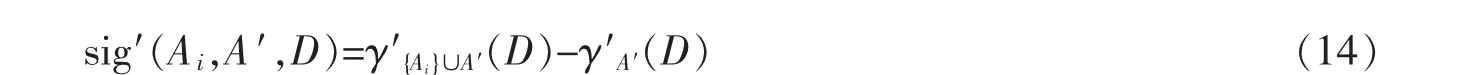
最后，通過定義14 來計(jì)算表1 中的sig′（A1，A，D）=2/81，sig′（A2，A，D）=7/81（即β=0.4 時(shí)，A1，A3對(duì)D 的依賴度分別是2/81，7/81）。 根據(jù)定義14 計(jì)算的結(jié)果可以區(qū)分兩個(gè)粒度的依賴度，更符合實(shí)際應(yīng)用。

3.2 粒度重要性公式的改進(jìn)

為進(jìn)一步區(qū)分不同粒度的重要性，加入可信系數(shù)計(jì)算粒度的重要性，使得粒度重要性計(jì)算結(jié)果更加合理。

定義16 （可信系數(shù)） 四元組S=（U，C∪D，V，f）是一個(gè)完備信息系統(tǒng)，A={A1，A2，A3，…，Am}為粒度集合，設(shè)A 中去掉一個(gè)屬性集Ai的一個(gè)子集P=A-{Ai}，那么P 關(guān)于U/A 的可信系數(shù)有如下定義

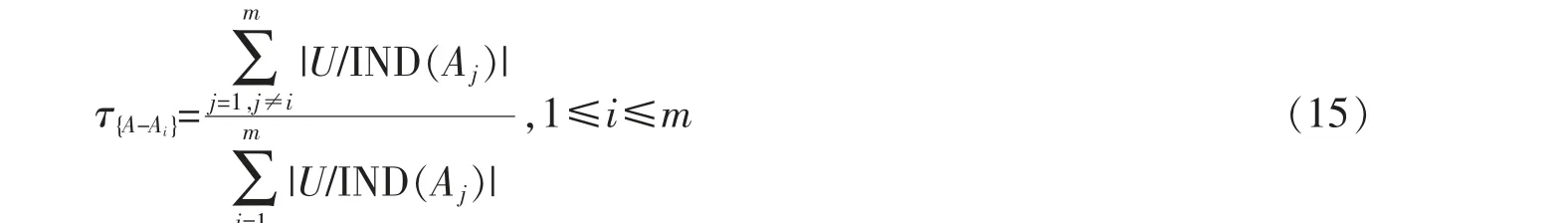
定理4 可信系數(shù)有如下性質(zhì)

證明 由定義16 顯然易證0＜τ{A-Ai}＜1。

定義17 四元組S=（U，C∪D，V，f）是一個(gè)完備信息系統(tǒng)，Ai∈A={A1，A2，A3，…，Am}，屬性D 導(dǎo)出的劃分為U/D＝{Y1，Y2，Y3，…，Yn}，Ai關(guān)于D 的粒度重要性定義如下

下面通過實(shí)例分析驗(yàn)證定義的可行性。

4 實(shí)例分析

表2 是一個(gè)學(xué)生面試的決策信息表，其中U={X1，X2，X3，X4，X5，X6，X7，X8，X9}為論域，表示參加面試的學(xué)生。條件屬性集C={a1，a2，a3，a4}表示不同學(xué)科的老師給出的專業(yè)評(píng)價(jià)，決策屬性d 表示學(xué)生面試是否通過，信息表見表2。

表2 決策信息表

令條件屬性集A={A1，A2，A3，A4}={{a1}，{a2}，{a3}，{a4}}。 有如下劃分

A-{A1}，A-{A2}，A-{A3}，A-{A4}關(guān)于U/A 的可信系數(shù)分別為3/4，3/4，3/4，3/4。

下面通過幾種確立粒度重要性的方法，結(jié)合上述分類信息進(jìn)行重要性的刻畫，得到結(jié)果見表3。

表3 各屬性重要性的對(duì)比

表3 中M 表示方法，方法1、2、3 分別對(duì)應(yīng)基于信息量的悲觀下近似度量（定義8）、基于下近似分布粒度熵的多粒度變精度度量（定義9）、文中提出的定義17。 在β，k的取值范圍選擇兩組參數(shù)，方法3 中β 的參數(shù)選取則是與方法2 中的參數(shù)k 是分別對(duì)應(yīng)的，當(dāng)k+β=1 時(shí)，兩種方法中的集合多數(shù)包含關(guān)系是一樣的，這樣求解的結(jié)果更具有對(duì)比性。 由表3 可見，依據(jù)方法1 求解時(shí)，只有粒度A1不為0，當(dāng)粒度重要度為0 時(shí)沒法區(qū)分各個(gè)粒度之間的重要性而且對(duì)粒度權(quán)重的計(jì)算有影響。 方法2 隨著參數(shù)k 取值的不同會(huì)影響到粒度重要性的變化，可以看出粒度集的重要性變化不大，有時(shí)也沒法區(qū)分粒度之間的重要性。

根據(jù)文中所提出的方法，可以直觀的表現(xiàn)出每個(gè)粒度的重要性的差別，為計(jì)算粒度的權(quán)重提供了依據(jù)。

5 結(jié)語

在近似依賴質(zhì)量的基礎(chǔ)上，引入多數(shù)包含度的概念，允許集合有一定程度的包含關(guān)系，并加入可信系數(shù)提出新的粒度重要性公式，并將它應(yīng)用在學(xué)生面試決策系統(tǒng)中說明它的可行性。 接下來的工作是將粒度重要性公式應(yīng)用到教學(xué)數(shù)據(jù)中，指導(dǎo)相關(guān)的教學(xué)工作和決策。