例析指數函數的圖像與性質問題

■歐陽亮

指數函數是高中數學的重要內容,也是高考的考查重點。下面舉例分析指數函數的圖像與性質的常見題型,供大家學習與提高。

題型1:根據函數判斷圖像

例1 已知1>n>m>0,則指數函數:①y=mx,②y=nx的圖像為( )。

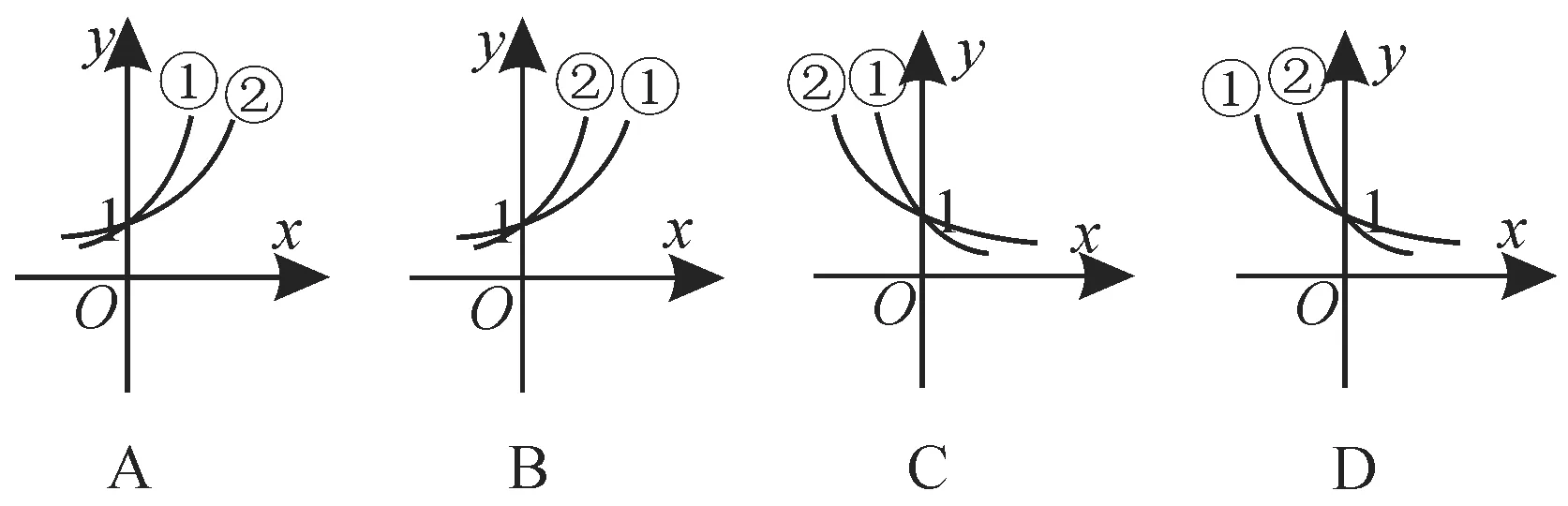
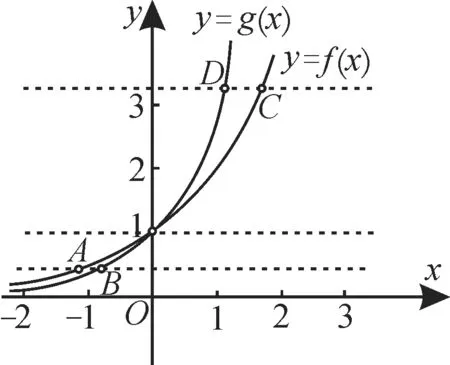
解:由0

評注:識別函數圖像可從以下幾個方面入手:(1)從函數的定義域,判斷圖像的左右位置,從函數的值域,判斷圖像的上下位置;(2)從函數的單調性,判斷圖像的變化趨勢;(3)從函數的奇偶性,判斷圖像的對稱性;(4)從函數的周期性,判斷圖像的循環往復;(5)從函數的特征點,排除不合要求的圖像。

題型2:函數的圖像恒過定點

例2 函數f(x)=ax-2021+2022(a>0,且a≠1)恒過的定點為____。

解:函數y=ax(a>0,且a≠1)的圖像恒過定點(0,1)。令x-2021=0 得x=2021,所以f(2021)=1+2022=2023。故函數f(x)=ax-2021+2022(a>0,且a≠1)恒過定點為(2021,2023)。

評注:本題也可令a=2和a=4,得到兩個關于x,y的方程,解出方程組可得圖像經過的定點坐標。

題型3:求參數的取值范圍

例 3 若 分 段 函 數f(x)=

解:當a>1時,f(x)在(-∞,-1)上是增函數,在[-1,+∞)上是減函數,則函數f(x)在R 上不是單調函數,可知a>1 不合題意;當0

評注:對數函數的底數中含有參數,解題時要注意分類討論,且分類要全面,做到不重不漏。

題型4:利用圖像比較大小

例4 已知實數a,b滿足等式2a=3b,給出下列五個關系式:①0

解:在同一直角坐標系中作出函數f(x)=2x,g(x)=3x的圖像,如圖1所示。

圖1

由圖可知,當直線AB位于y=1 下方時,交點A,B的函數值相等(2a=3b),但a

評注:比較指數式的大小的兩種方法:當底數相同時,運用指數函數的單調性求解;當底數不同時,利用一個中間量做比較進行求解,或借助于同一坐標系中的圖像求解。

題型5:指數函數圖像的平移變換

例5 為了得到函數y=ex-3+1 的圖像,只需把函數y=ex的圖像上所有的點( )。

A.向左平移3個單位長度,再向上平移1個單位長度

B.向右平移3個單位長度,再向上平移1個單位長度

C.向左平移3個單位長度,再向下平移1個單位長度

D.向右平移3個單位長度,再向下平移1個單位長度

解:函數y=ex的圖像向右平移3 個單位長度到得函數y=ex-3的圖像,再向上平移1個單位長度得到函數y=ex-3+1的圖像。應選A。

評注:把y=f(x)的圖像向左平移a(a>0)個單位長度得到函數y=f(x+a)的圖像;把y=f(x)的圖像向右平移a(a>0)個單位長度得到函數y=f(x-a)的圖像;把y=f(x)的圖像向上平移a(a>0)個單位長度得到函數y=f(x)+a的圖像;把y=f(x)的圖像向下平移a(a>0)個單位長度得到函數y=f(x)-a的圖像。

題型6:求函數的單調區間的增區間為(-∞,1],所以函數f(x)的減區間為(-∞,1]。

評注:求解與指數函數有關的復合函數問題,要明確復合函數的構成,涉及值域、單調區間、最值等問題時,都要借助“同增異減”的法則進行判斷。

1.若函數y=ax+b-1(a>0,且a≠1)的圖像經過第二、三、四象限,則一定有( )。

A.00

B.a>1,且b>0

C.0

D.a>1,且b<0

圖2