例析求對數型函數的參數取值范圍問題

■危先興

求參數取值范圍問題是同學們學習中的一個難點,這類問題是高考的常考點。其中求對數型函數的參數取值范圍問題就是一類重要的題型。下面舉例分析,供同學們學習與提高。

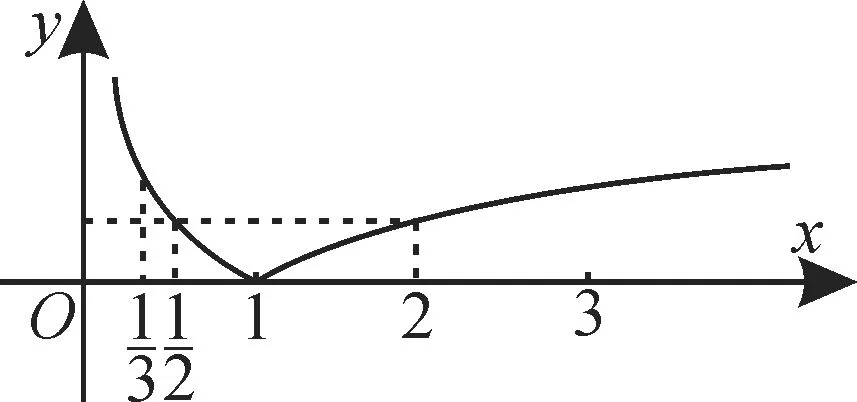
例1 若不等式(x-1)2

解:設f1(x)=(x-1)2,f2(x)=logax,要使當x∈(1,2)時,不等式(x-1)2

當01時,兩個函數的圖像,如圖1所示。

要使當x∈(1,2)時,f1(x)=(x-1)2的圖像在f2(x)=logax圖像的下方,只需f1(2)≤f2(2),即(2-1)2≤loga2,可 得loga2≥1,解得a≤2,所以1

故實數a的取值范圍是(1,2]。

圖2

求對數型函數的參數取值范圍問題應注意以下三點:(1)注意數形結合思想的應用;(2)注意分類討論思想的應用;(3)注意函數奇偶性、單調性的應用。