社群化制造中眾包設計任務間模糊加權圖建模與優化重組
劉電霆, 胡浩平, 吳丹玲
(1.桂林理工大學 機械與控制工程學院, 廣西 桂林 541006; 2.深圳信息職業技術學院 財經學院, 廣東 深圳 518172)
0 引 言
社群化制造(social manufacturing)[1-2]泛指人人都可參與產品生產的一種制造模式, 是一種涉及產品整個生命周期的廣義制造[3]。它包括個人或設計單位根據需求提出的眾包設計[1], 為中小企業走出資源、技術和創新等不足的困境創造了條件。
現代產品越來越復雜, 按眾包設計方式, 其總任務需要被細分成許多原子任務才能通過眾包平臺找到合適的個體設計者。然而, 有些原子任務所對應的產品零部件, 可能存在功能、結構等關聯, 引起設計人員之間頻繁的溝通交流。為此, 通常需要將它們重組為虛擬模塊, 由相應的設計人員構建虛擬社群來協作設計, 這是社群化制造中產品眾包設計過程的一個關鍵問題[1, 4-5]。
對于產品眾包設計任務的劃分與重組, 通常先采用功能分解法和結構分解法進行產品任務分解[6]。前者是按照產品組合過程中多個任務單元所具備的功能進行分解, 后者按照產品任務結構相關度進行分解。一個產品由多個部件組成, 一個部件又由多個零件組成, 由此得到一個產品的組成結構樹;然后采用設計結構矩陣(design structure matrix, DSM)[7]及其改進的區間數設計結構矩陣IDSM[8]和模糊設計結構矩陣FDSM[9]等這些部件的原子設計任務之間的關系進行描述; 再依據任務之間的關系緊密度, 按一定的規則進行重組, 得到產品設計的若干子任務模塊;最后, 對這些子任務模塊進行描述, 構成相應的產品眾包設計任務。
設計結構矩陣DSM的直觀性不是很強, 需要尋找其他方法來描述原子設計任務之間的關系,最常用的是圖論法, 如Duin等[10]和胡從林等[11]采用有向圖來描述原子設計任務之間的關系, 然后從中得到可達矩陣, 再由此將其聚類成若干子任務模塊。陳健等[12]使用權重有向圖來描述原子設計任務之間的關聯, 并將其轉換成DSM, 再由此來重組任務模塊。
相比設計結構矩陣, 采用圖論法來描述原子設計任務之間的關系更直觀明了、易于理解。然而對于產品設計, 尤其是新產品開發或改型設計, 原子任務之間的關系無法事先準確知道, 具有不確定性。為此, 本文采用模糊加權圖來描述原子任務之間的關系, 并主要依據模塊內聚合度、模塊間耦合度和模塊規模適應難度等對眾包設計原子任務進行聚類, 重組為若干虛擬模塊。
1 眾包設計原子任務間的模糊加權圖建模
1.1 眾包設計原子任務間的相關度
越來越復雜的當代產品, 從結構上來看, 一般由許多零部件組成。采用眾包方式進行設計時, 將與各個不能再細分的產品基本單元(一般是零部件)相對應的設計任務, 設定為產品眾包設計的原子任務。產品基本單元存在功能、結構等方面的關聯, 一般難以給出具體精確的值。通過相關性分析, 結合原子任務兩兩之間的關聯度, 可用5級標度的三角模糊數[0.6, 0.8, 1.0]、[0.4, 0.6, 0.8]、[0.2, 0.4, 0.6]、[0.0, 0.2, 0.4]和[0.0, 0.0, 0.0]來表達[13-14]。
對產品眾包設計的原子任務, 它們之間的相關度可按照三角模糊數的運算法則[15]進行計算
(1)
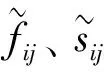
1.2 眾包設計原子任務間模糊加權圖建模
1.2.1 模糊加權圖的構造 以眾包設計的原子任務為節點,它們之間聯系為邊、相關度為邊的權值, 則可以構造原子任務間的加權圖。本文采用5級標度的三角模糊數來描述原子任務之間的關聯, 模糊加權圖如圖1所示。其中的16個節點表示16個原子任務,兩兩節點連接邊上的數字表示原子任務間的相關度(即已進行處理之后的三角模糊數)。
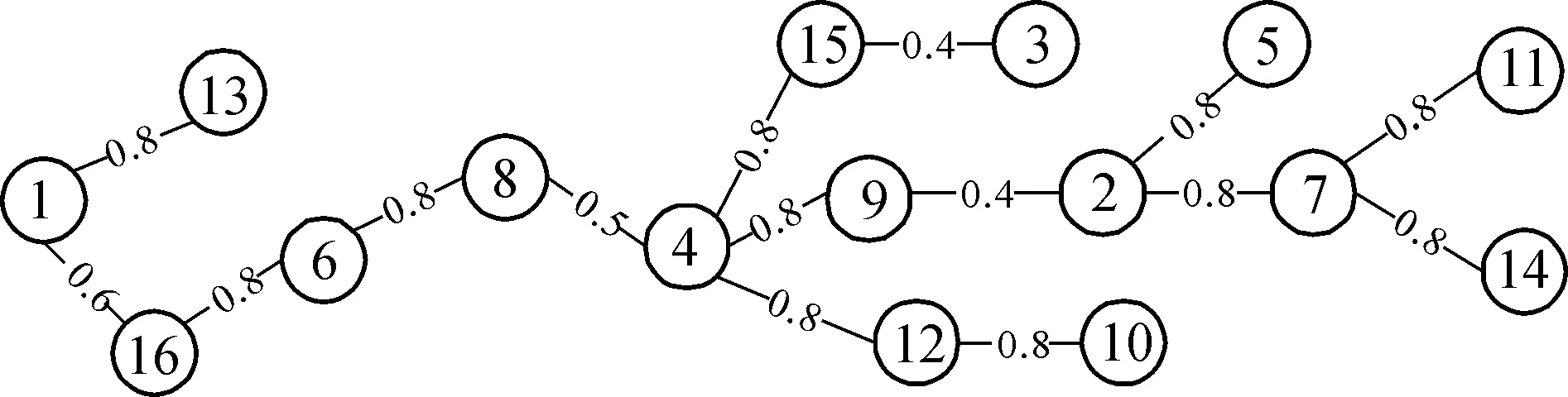
圖1 模糊加權圖
1.2.2 模糊加權圖的剪枝 按照一定的粒度閾值a0,對上述模糊加權圖去掉相關度小于a0的邊,本文取粒度閾值a0=0.6,則得到相應的剪枝圖(圖2)。
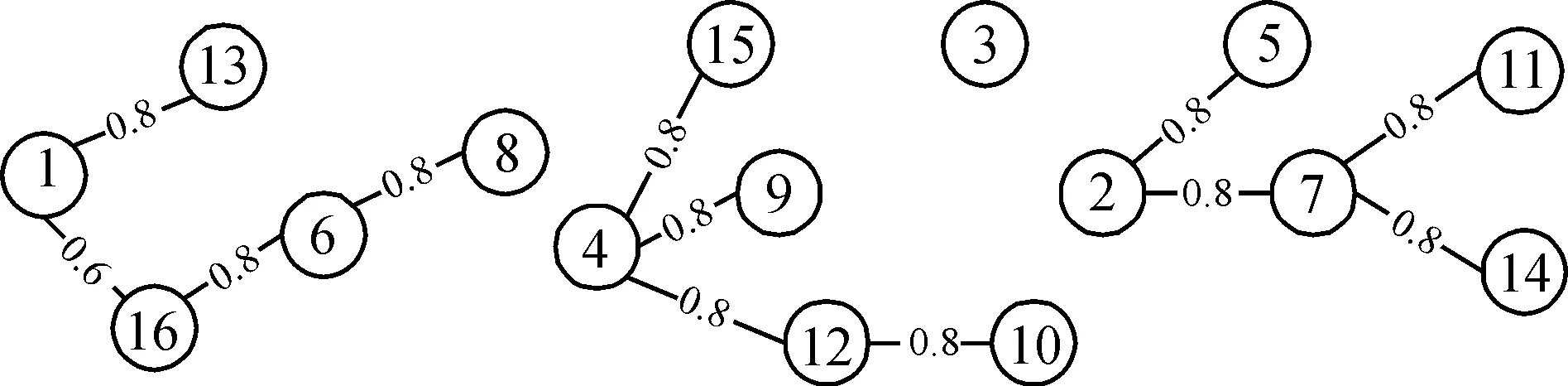
圖2 剪枝加權圖
可知, 經剪枝后分為4個子任務模塊, 分別為(1, 6, 8, 13, 16)、(3)、(2, 5, 7, 11, 14)和(4, 9,10, 12, 15)。
2 眾包設計原子任務的虛擬重組原理
2.1 眾包設計原子任務虛擬重組原則與步驟
目前越來越復雜的產品中, 有些產品基本單元在功能、結構上關聯比較緊密, 需要設計人員隨時溝通,交流意見,在完成各自設計任務的同時, 達到局部上各產品基本單元、整體上相關聯產品的基本單元都滿意的設計效果。這也符合社群化制造模式的共享、交互、協作等主要特征。
由于在社群化制造中, 這些原子任務聚合成虛擬模塊, 由相應的設計人員構建社群來協作設計,所以要求其規模較合理、結構相對完整和功能相對獨立, 以便其能在設計者構成的社群中被順利地接受和執行完成。因此, 眾包設計原子任務的虛擬重組原則是: 滿足其所設計產品模塊的功能獨立性和結構完整性; 眾包設計虛擬模塊之間耦合度盡量小,而模塊內部原子任務之間的聚合度盡可能大, 且找到適當的模塊規模。
按照產品模塊的特性及其設計任務虛擬重組的原則, 原子任務虛擬重組的步驟主要有: ①分解得到原子任務; ②構造描述原子任務之間關系的模糊加權圖; ③對該圖進行剪枝;④建立該圖剪枝的數學模型, 并進行優化求解, 得到最終的虛擬模塊方案等。
2.2 虛擬模塊內部聚合度和模塊之間耦合度
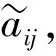
(2)
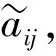
(3)
所有虛擬模塊間的總耦合度為
(4)
2.3 眾包設計任務虛擬模塊規模的適應難度
產品眾包設計原子任務重組為虛擬模塊, 需要由多人組成社群來協作設計。若模塊規模過大, 則需要的社群成員過多, 社群內交流和沖突也太多, 不利于模塊的整體設計進度和質量等, 即模塊規模適應難度低。要實現最高的團隊效率, 需要最佳的團隊成員數量為P*, 一般為4~6人[16],所以模塊規模應當控制在5人左右。為此, 在進行模糊加權圖的剪枝時, 模塊規模的適應難度(R)指標定義為
式中:Pi為第i個模塊所含原子任務數;Pmax為最大模塊規模(即原子任務總數);M為模塊總數。
3 眾包設計原子任務虛擬重組的優化
3.1 眾包設計原子任務虛擬重組的優化模型
根據產品眾包設計原子任務重組原則, 虛擬模塊內部聚合度應最大, 模塊之間的耦合度應最小, 模塊規模的適應難度最低, 則原子任務虛擬重組的不確定優化模型為
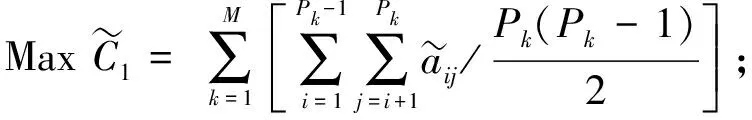
(5)
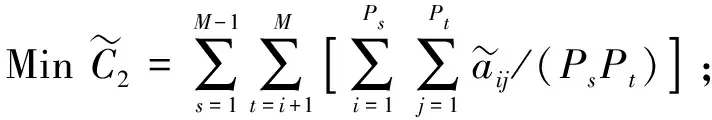
(6)
(7)
3.2 眾包設計原子任務虛擬重組優化模型的求解
3.2.1 不確定模型的轉換 依照三角模糊數的運算法則[15], 進行該不確定優化模型內部的數據計算,并按加權重心法[15]將其轉為確定數值。據此,把式(5)~(7)轉換成確定型優化模型。
3.2.2 優化重組模型的蟻群算法求解 任務重組問題具有組合最優化特性, 是NP-Hard問題, 宜利用蟻群算法求解。本文的求解步驟為:
① 初始化各個參數以及相關數據。
② 循環迭代開始。
③ 隨機安置螞蟻于各個點上, 初始化相關計算用表。
④ 計算最大轉移概率的節點作為最佳選擇, 同時與rand()進行比較, 從而重組到不同模塊。
(8)
其中,γij(t)、ηij(t)、α、β為相應的信息素、相關性和相關啟發因子。
⑤ 若全部頂點仍未被每只螞蟻遍歷完, 則繼續③,否則⑥。
⑥ 對稱更新信息素
γij(t+n)=(1-ρ)·γij(t)+Δγij(t);
(9)
(10)
(11)
其中:m為螞蟻數;n代表路徑;ρ為蟻群模型中的信息取值;Q為常量;Lk是適應度值(由式(12)計算所得的F值經數據格式化后可得Lk)。多目標式(5)、(6)、(7)根據權重比例轉為了單目標模型,即
F=w1C1-w2C2-w3R。
(12)
⑦ 迭代完成則結束,并把最優解輸出,未完則轉到步驟②。
4 實例分析
4.1 問題描述
以某起重機橋梁設計總任務為實例[17], 共有11個原子任務: 1主梁子任務、2軌道子任務、3端梁子任務、4端梁欄桿子任務、5走臺子任務、6走臺欄桿子任務、7直梯子任務、8斜梯子任務、9司機室平臺子任務、10司機室子任務、11檢驗平臺子任務,分別用T1,T2,T3,T4,T5,T6,T7,T8,T9,T10,T11表示。功能相關度和結構相關度分別存于表1中上三角形與下三角形。
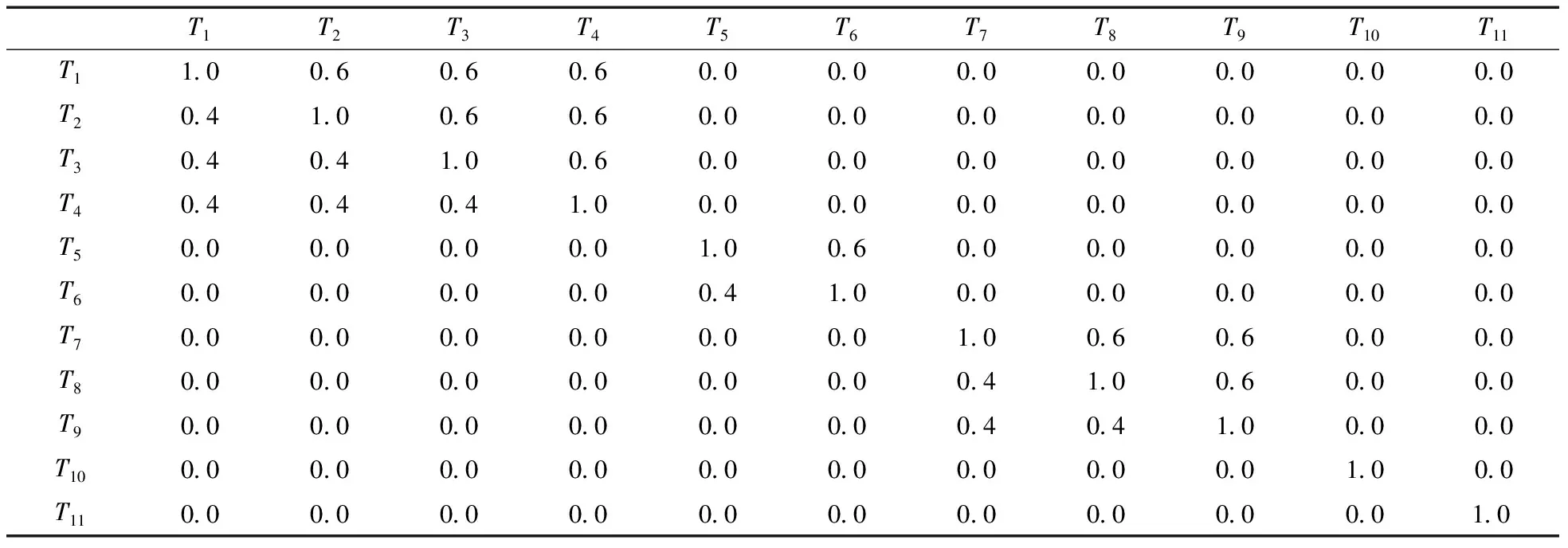
表1 功能相關度和結構相關度
4.2 實驗數據
用C語言編寫程序, 初始化離散的11位數字編碼分別與T1,T2,T3,T4,T5,T6,T7,T8,T9,T10,T11一一對應, 迭代次數均為500次, 設置不同參數獲得的實驗結果見表2。
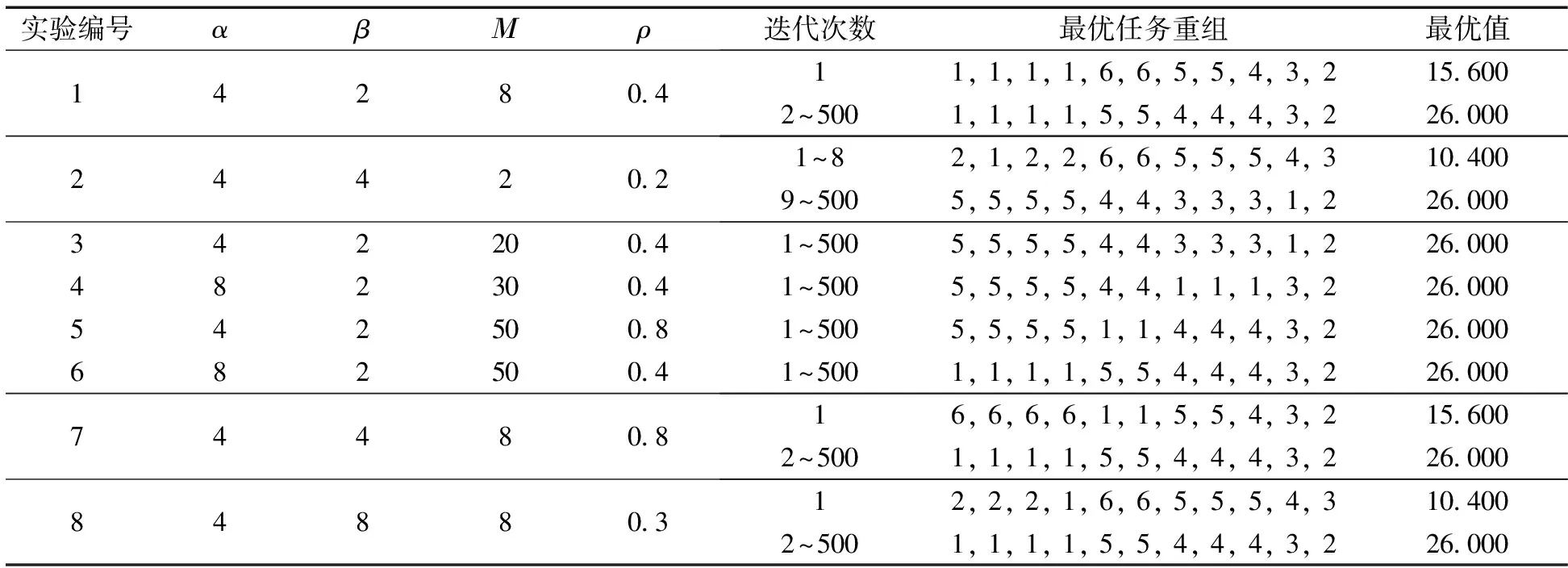
表2 實驗結果
可知, 該方法充分發揮了蟻群智能算法的優點, 很快得到收斂, 迭代次數增加而收斂值不變, 同實驗設置不同的參數, 所獲得的最優適應值均為26.000, 說明該方法的穩定性較好; 求得最佳重組虛擬模塊:T1,T2,T3,T4,T5,T6,T7,T8,T9,T10,T11所一一對應的幾組實驗求解結果分別是{5, 5, 5, 5, 4, 4, 3, 3, 3, 1, 2}、{1, 1, 1, 1, 5, 5, 4, 4, 4, 3, 2}、{5, 5, 5, 5, 4, 4, 1, 1, 1, 3, 2},其中每組最大數字5表示該求解結果劃分為5個模塊, 相同數字為同一模塊:即T1、T2、T3、T4為同組,T5、T6為同組,T7、T8、T9為同組,T10、T11各為一組。具體實例最優重組的虛擬模塊是{直梯,斜梯,司機室平臺}為同組, {主梁,軌道,端梁,端梁欄桿}為同組, {司機室}、{檢驗平臺}各為一組, {走臺,走臺欄桿}為一組,結果與文獻[17]中λ=0.625時劃分結果相同, 由于本方法研究的側重點和求解模式不同, 獲得的結果具備唯一性, 對行業的產品任務重組存在借鑒和指導作用。
5 結 論
本文提出了一種基于模糊加權圖的產品眾包設計的原子任務之間關系建模與優化重組方法。對眾包平臺設計任務中考慮其任務單元的功能和結構相關性, 構建多目標不確定優化模型; 同時, 將多目標轉化為單目標模型, 采用蟻群算法求解, 實例測試,結果符合實際要求。
進行社群制造中協作設計時, 做好成員企業內部設計原子任務間的關系描述與重組是關鍵技術之一。根據本文提出的眾包設計中任務虛擬模塊重組的不確定優化方法, 結合中小企業協同網絡平臺, 可使產品眾包設計任務推送更加智能化和自動化。
隨著眾包任務設計的復雜性增加, 云計算大數據的軟硬件技術支撐, 互聯網+眾包任務分配必將更智能、更科學合理。下一步將引入Pareto最優解尋求更合理的多目標解, 同時將研究更復雜的任務分配問題。

