基于雙層神經網絡模型參數辨識的變結構多模型自主導航方法

許曉偉，賴際舟，呂 品，陸俊清，白師宇，胡華峰

（1.南京航空航天大學 自動化學院，南京 210096；2.湖北航天技術研究院 總體設計所，武漢 430040）

井下的煤炭開采的作業空間狹小，工作人員靠近大型機械，以及空氣中存在的易燃易爆氣體和粉塵都對井下安全帶來了挑戰。為了確保采煤效率和工人的工作安全，煤炭開采正在由人工向自動化方向轉變，其中采煤機定位是實現煤炭開采自動化的核心技術[1,2]。在GNSS拒止的井下定位環境中，慣導系統憑借其較好的自主性和可靠性被廣泛應用于井下的復雜環境[3,4]。為了提高慣導系統的定位精度，零速校正是一種常用的誤差約束手段，但這種方式需要載體不斷地靜止實現載體的速度約束，不利于采煤機的連續開采。楊海等人[5]通過對采煤機振動引起的慣導系統計算誤差進行了相關研究，通過對振動頻譜特性的分析，建立了圓錐誤差和劃船誤差的補償模型，利用多子樣算法提高了慣導系統的計算精度。但是在隨機振動中，多子樣補償算法的效果不明顯[6]。受制于慣導系統自身定位機理，長時間的采煤過程導致慣導系統定位誤差不斷累積[7]。為保證慣導系統長期的定位精度，通常需要借助外部信息的周期性的修正慣性誤差。例如通過里程計和慣導系統的組合，減少了采煤機長時間切割過程中的位置發散，或者利用在井下環境中布置的UWB錨節點組成無線傳感網絡實現對慣導位置的約束[8]。Jonathon R等人利用熱成像相機，利用采煤機煤炭切割過程中截割部與不同成分的煤層摩擦產生的不同紅外特性，提高了煤層垂直面位置的定位精度[9]。由于井下惡劣的環境對傳感器的可用性、可靠性和安全性都提出了嚴格的要求。因此目前基于慣導/里程計的組合導航仍是最主要的導航方式。

為了分析井下慣導系統在振動環境下的輸出特性，采用陀螺零偏穩定性為0.003°/h的慣導在某礦井下采集了采煤機工作時的實際陀螺輸出，如圖1、2所示。

圖1 井下開采靜止狀態陀螺實際輸出Fig.1 The output of the gyro at static state

圖2 井下開采切割狀態陀螺實際輸出Fig.2 Output of gyro under vibration

從圖中可以看出，開采靜止狀態的陀螺輸出基本符合慣導標稱的性能水平。但是在切割狀態下，慣導系統由于振動使陀螺輸出精度存在明顯下降。圖3是實際開采過程中慣導系統陀螺儀在井下振動環境的噪聲頻譜圖，其中存在著多種不同的振動頻率分量，導致噪聲水平多變。

圖3 井下開采實際陀螺噪聲頻譜Fig.3 Spectrum of noise under vibration

目前傳統的卡爾曼濾波估計通常基于固定噪聲模型，在濾波過程中由于模型參數失配導致濾波結果精度較差甚至發散，難以適用于井下定位環境。多模型估計（Multiple Model Estimation, MME）是一種能夠處理系統結構和參數不確定的自適應估計方法[10]，被廣泛用于時變模型的故障檢測和診斷[11]、目標跟蹤[12]、組合導航[13,14]等領域。為了解決輪式里程計在輪胎出現滑動時誤差時變的問題，Hyoungki Lee等人[15]提出了一種交互式多模型的輪式里程計滑移檢測及補償方法，利用基于模糊邏輯輔助的交互式多模型逼近無滑移和滑移過程中的時變動力學模型，提高了載體的定位精度。為了解決GPS拒止的巷道環境下的車輛多動態高精度定位，王磊等人[16]針對組合導航系統中存在的時變或非高斯噪聲，提出了一種交互式多模型秩濾波算法，實驗結果表明算法能夠提高組合導航系統姿態、速度和位置估計精度。但是，傳統固定結構多模型算法均針對較少的系統狀態。當時變系統運動狀態需要較多的模型集合來描述時，不僅計算更加復雜，而且模型之間的競爭會導致系統狀態的估計精度下降。變結構多模型算法針對更加復雜的目標運動狀態，能夠在不增加計算復雜度的情況下提高系統性能[17]。由于煤層復雜的組成成分以及機體的自身振動，導致采煤機在切割過程中的系統噪聲呈現時變特點，變結構多模型估計算法能全面地描述不同開采工序下的采煤機系統模型參數，提高采煤機的導航定位精度[18,19]。但目前仍然沒有有效理論指導模型集的設計，不能保證模型切換的時效性和正確率。

因此，本文針對井下復雜的振動環境，設計了基于變結構多模型的定位方案。對傳統基于后驗概率進行模型切換的模型識別算法進行改進，提出了基于支持向量機（Support Vector Machine, SVM）和極限學習機（Extreme Learning Machine, ELM）相結合的雙層神經網絡模型參數辨識算法。實現快速準確的最佳模型集選擇以及模型集的激活和終止。相較于傳統模型集在線選擇算法[20]具有更快的模型切換效率和更高的準確性，提高了井下復雜環境慣導/里程計組合導航的定位精度。

1 慣導/里程計井下定位方案

綜合機械化采煤是一種利用機械化和自動化設備進行采煤工作的過程。設備主要包括常用的滾筒式采煤機、刮板輸送機和液壓支架，通過三者之間的緊密配合，實現破煤、運煤和支護任務，具體結構如圖4所示。綜合機械化采煤切割面大約有200-450 m寬，長度可以達到5 km，采煤機每次大約切割0.8 m厚的煤層，每次采煤機開機進行煤炭切割，都需要切割數百米的煤層，時間長達數小時。采煤機在開采過程中存在靜止、前進、倒退等不同的運動狀態，對應著不同的切割過程。由于采煤機切割過程中煤層成分的不確定導致截割部的受力變化，采煤機工作過程中會產生不同程度的機械振動，導致器件時變誤差特性時變。

圖4 綜合機械化采煤切割面結構Fig.4 Structure of fully mechanized coal mining face

井下惡劣環境對于傳感器的選擇提出了苛刻的要求。需要在能夠保證井下安全的基礎上，提供可靠的導航信息。其中，無線電定位容易在巷道中產生多路徑和非視距效應，甚至信號被完全遮擋。視覺傳感器和激光雷達等主動傳感器容易被粉塵、泥漿等環境影響，可靠性和精度難以保證，因此并未得到廣泛應用。

慣導系統更新頻率快，短時精度高，能夠獲得采煤機三維的速度、位置和姿態。里程計受采煤機振動的影響小，誤差的發散特性與其運動距離相關，適合采煤機這種工作時間長，運動相對較慢的載體，能夠在較長時間保持較高的定位精度。基于卡爾曼濾波的慣導/里程計組合導航方案被廣泛應用于井下采煤機定位。由于沒有考慮采煤機開采過程的時變噪聲對組合導航精度帶來的影響，導致采煤機的定位精度難以滿足實際的工程需求。綜上，本文設計了基于雙層神經網絡模型參數辨識的慣導/里程計井下融合方案，綜合機械化采煤結構和組合方案如圖5所示。

圖5 綜合機械化采煤導航系統結構和組合方案Fig.5 Structure and combination scheme of the navigation system for fully mechanized mining

2 基于雙層神經網絡模型參數辨識的改進變結構多模型方法

傳統的模型集切換方法通常采用可能模型集算法（Likely Model Set, LMS）以及模型組切換算法（Model Group Switching, MGS），其中現有模型選擇策略較多，但沒有一種經典理論指導模型集合的在線選擇，模型集自適應選擇正確率和時效性不能得到保證。傳統算法為了盡量保證模型參數的匹配，會傾向于選擇模型較多的集合，因此這種模型集選擇的取向會在狀態估計和基于新激活的模型的濾波器的協方差中帶入誤差，導致濾波精度下降[20]。本文結合井下采煤工作時的運動特性，通過對可能模型集算法的改進，提出了基于雙層神經網絡模型參數辨識的改進變結構多模型方法，具體結構如圖6所示。

圖6 基于雙層神經網絡模型參數辨識的變結構多模型框架圖Fig.6 Block diagram of Two-Layer Network Identification based Variable Structure Multi-Model

2.1 基于雙層神經網絡的多模型參數辨識算法

系統噪聲的模型參數隨著采煤機的不同運動狀態產生相應的變化，因此我們根據采煤機的切割、倒車和停止等多個狀態下的系統模型進行分類，這類系統噪聲之間的區別明顯，單層的神經網絡分類算法可以較為準確的識別。但即使處在同一運動狀態下時，采煤機的振動變化會導致系統模型發生改變，這種變化相對于不同運動狀態下采煤機系統噪聲尺度變化小。當這些不同級別的系統噪聲全部用于對單層的神經網絡分類算法的訓練時，由于不同數量級辨識的尺度不同，模型參數辨識的精度出現了明顯的下降，存在同量級的模型噪聲混淆的問題。為了提高模型的辨識精度，提出一種將SVM和ELM結合的雙層神經網絡模型參數辨識算法。

圖7 采煤機開采噪聲模型雙層神經網絡辨識算法Fig.7 Two-layer neural network identification algorithm for mining noise model of shearer

雙層神經網絡模型參數辨識算法包括兩層分類處理，兩層分類依次銜接，構成了針對噪聲量級的初步辨識和同一量級的細分辨識，構成完整噪聲模型識別方案。大尺度粗辨識數據量較大，一旦出現辨識錯誤將影響后續的第二層辨識，因此需要足夠的穩定性。考慮到增加辨識層會導致系統計算量的增加，第二層神經網絡分類算法應當具備較快的辨識速度，從而保證系統的實時性。本文針對大尺度粗辨識的穩定性以及小尺度精辨識的小樣本特點，首先利用SVM識別噪聲所屬量級，然后針對已經根據運動狀態分類的同一數量級特征采用相應的ELM分類模型進行具體的噪聲模型識別。

SVM算法本質是在樣本空間中找到一個超平面，將不同類別的樣本分開。通過找到“最大間隔”超平面，使得分類結果具有魯棒性，泛化性能最好，同時分類性能穩定。首先假設分離超平面為：

點到平面距離為：

其中＜w,x＞為向量點積，當兩類樣本線性可分時，設滿足以下條件：

假設兩個平行超平面H1和H2作為間隔邊界以判斷樣本分類：

超平面H1和H2到原點的距離分別為和因此H1和H2的間距為時，分類間隔最大就是使最小，即：

其中w為法向量，ωs決定了超平面的方向，bs為位移項，ωs通過和sb確定劃分超平面。對于提取的慣導數據特征，采用SVM進行初步分類。將多分類簡化為多個二分類，采用的輸出為0、1輸出。

第二層模型參數辨識網絡通過ELM與上層辨識結構相連，其模型如圖8所示，通過隨機初始化單隱層神經網絡的輸入權重和偏置得到相應的輸出權重，具有學習速度和運算速度快的優勢，適合處理小樣本數據。

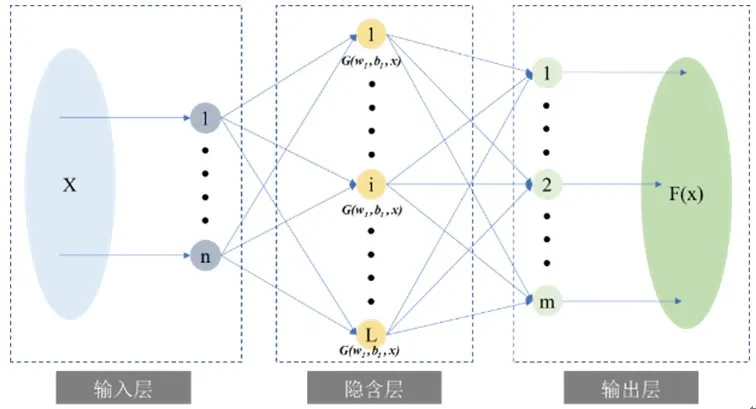
圖8 極限學習機結構圖Fig.8 Structure diagram of extreme learning machine

針對已經由上層辨識網絡獲得的不同數量級噪聲，訓練多個獨立的分類模型。對于上述的每一個類別，給定采集的N個訓練樣本(XNN,TNN) = ｛(xi,ti),i=1,2...N｝，此處XNN為提取的噪聲特征矩陣，TNN為對應的期望輸出，N為該類別輸入的樣本個數，xi=[xi1,xi2,...,xin]T表示XNN中的第i個樣本，n為輸入的樣本維，ti=[ti1,ti2,...,tim]T表示第i個樣本的對應輸出，m表示輸出的向量維（與噪聲類別相同）。在本文中，期望輸出向量采用0、1標記方式標定，即樣本屬于第幾類噪聲模型，則將期望輸出向量位置中的第幾位標記為"1"，其余位全均記為"0"。設單隱層神經網絡的隱含層有L個節點，其輸出為：

其中，ωi為連接輸入神經元與第i個隱含層節點的權向量，bi為第i個隱含層節點的偏置，βi是第i個隱含層節點的輸出權向量，g()·為激活函數。因此，可將式(8)簡化成：

其中，H是隱層節點的輸出，β為輸出權重，O為單隱層神經網絡的輸出。

ELM的學習目標是通過最小化預測誤差損失函數之和來求解輸出權重，其運用最小范數得到最小誤差解：

因此根據上述公式可以推導出隱含神經元與輸出神經元的輸出權值矩陣最優解：

其中H+是矩陣H的摩爾-彭羅斯廣義逆。通過雙層神經網絡模型參數辨識獲得當前運動狀態的模型參數，從模型庫中選取與該參數標準差最小的多個模型組成模型集合帶入變結構多模型算法，對當前采煤機的運動狀態進行估計。

根據數據特征構建的雙層神經網絡模型參數辨識充分利用不同神經網絡分類算法的優勢，解決了傳統模型自適應完全依賴于后驗概率模型導致的模型切換準確性和實時性難以保證的問題，能夠有效避免模型誤匹配帶來的濾波器發散。同時相較于單層模型參數辨識神經網絡，提高了小尺度模型之間的辨識精度，兼顧了多層神經網絡的辨識效率。

2.2 基于模型參數辨識的改進變結構多模型算法

2.2.1 系統及量測模型構建

本文基于東北天導航坐標系來討論。為了描述采煤機的運動狀態和慣性儀表誤差以及里程計標度因數誤差，考慮狀態量設置如下：

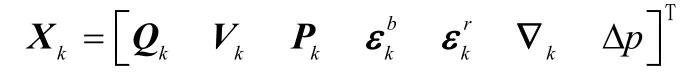
其中，Qk= ［q1(k)q2(k)q3(k)q4(k)］為k時刻姿態四元數，為k時刻載體東向、北向及天向速度；Pk=［λ(k)L(k)h(k)］分別是經度、緯度和高度，和分別為3個軸向的陀螺儀的隨機常值零偏和一階馬爾可夫隨機噪聲，分別為3個軸向加速度計的一階馬爾可夫隨機噪聲，pΔ是里程計的標度因數誤差。

里程計每個采樣周期輸出的量測量如下：

對ITC數據進行切片,采用MATLAB對其進行可視化,得到網絡快照集合{G1,G2,…,Gn},G1表示初始時刻的網絡拓撲圖,G2表示時隔一個切片時長后的拓撲圖,依次類推,Gn表示最后一張拓撲圖,其演化過程如圖4 (a)～(c)所示.

里程計的位置遞推公式如下：

其中，Mk和Mk-1分別是k和k-1時刻的脈沖數，Pk和Pk-1為k和k-1時刻導航系下采煤機的位置，為k-1時刻的姿態轉移矩陣，p為里程計的標度因數，Δp是標度因數誤差。濾波時將導航系下的預測位置轉化為地心地固坐標系下的經度、緯度和高度。本文采用直接法進行擴展卡爾曼濾波，狀態方程和量測方程構建可以參考文獻[21]。

2.2.2 變結構多模型算法

從量測模型可以看出，里程計的位置精度不僅取決于自身輸出，也受到載體姿態的影響。其中，航向角對里程計水平位置輸出的精度有直接影響。當系統噪聲模型和量測噪聲模型不準確時，系統難以準確估計預測和量測的誤差水平，使系統狀態估計精度下降，同時將不準確的航向信息再耦合進里程計量測中，導致量測的精度也難以保證。因此建立多個系統模型達到逼近實際模型的目的，有效降低了濾波器對系統數學模型的依賴性，有利于提高組合導航系統的濾波精度。

變結構多模型算法能夠在沒有準確系統模型和先驗知識的情況下通過多個模型之間的自適應，避免模型失配導致濾波器發散。變結構多模型由多個并行的擴展卡爾曼濾波器組成，根據模型集自適應算法選出當前適合的模型集，將最優模型集帶入濾波器，通過不同濾波器之間的殘差和方差獲得對應模型的似然函數即條件概率密度函數，進而通過貝葉斯公式計算各個模型的概率。最后將上一時刻的狀態估計和模型概率轉化為權重，初始化當前狀態及其協方差陣。具體計算步驟如下所示。

（1） 交互輸入

利用上一個周期的狀態和模型轉移概率獲得當前時刻的交互輸入，初始模型轉移概率為：

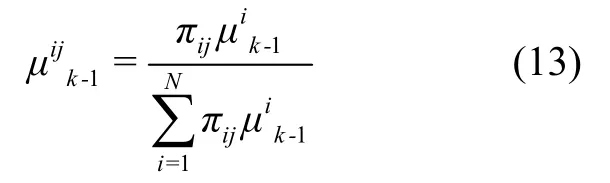
根據模型條件轉移概率重新初始化模型j的狀態與協方差陣為：

（2） 模型濾波

根據上述擴展卡爾曼濾波的過程，帶入辨識后的噪聲模型，計算模型的濾波殘差和方差：

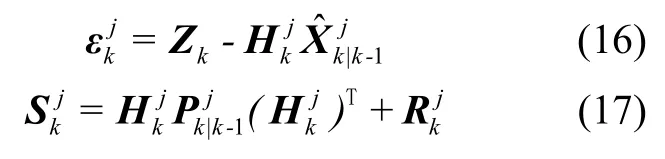
（3） 模型概率更新

根據假設檢驗原理，如果統計模型與實際模型匹配，則濾波殘差服從零均值高斯分布，由此獲得該模型的似然函數為：

模型概率可更新為：

其中，πij表示先驗的Markov模型轉移概率，為k-1時刻i模型的概率。

當模型檢測算法檢測到模型需要切換后，在當前運行模型中引入新的模型，重新分配新舊模型的權重，運行兩個模型集的并集。計算新模型集合和舊模型集合的概率，當新模型概率占總模型概率達到一定閾值時，丟棄舊模型，繼續運行新模型，通常閾值稍小于1，防止模型的直接切換可能帶來的模型跳變。最后對每個模型的濾波狀態進行加權，獲得全局的狀態估計。

3 仿真與分析

3.1 參數設置

為了驗證本文提出的算法性能，通過MATLAB對算法進行仿真。平臺搭載intel i7 8700k處理器，主頻3.7 Ghz。根據采煤的實際工況，將其開采流程分為3個步驟。首先是對工作面的水平切割，隨后進行斜切進刀工序，進刀距離1 m，進刀完成后切割三角煤，重新回到端頭進行下一次的切割。但在切割過程中可能由于煤層中的雜質等影響，導致采煤機暫停切割和倒退。每個工序根據采煤機與煤層接觸所產生振動情況設計相應的模型噪聲以及采煤機可能的實際運動狀態進行仿真，仿真傳感器主要包括高精度慣導系統和里程計。慣導系統的解算周期是0.02 s，里程計的解算周期是1 s，濾波周期與里程計解算周期相同。仿真軌跡按照實際可能的采煤機運動狀態進行模擬。在煤炭切割狀態速度為0.1 m/s，進刀狀態按照0.01 m/s。采煤機沿400 m切割面做往復運動，每次切割完畢向煤層推進0.9 m。全程共用4.4 h。變結構多模型算法模型集合切換閾值設置為0.8，初始馬爾可夫轉移概率設置為：

真實運動軌跡設計如圖9所示，傳感器參數和多模型算法參數如表1所示。

表1 傳感器參數設置Tab.1 Parameters setting of sensors

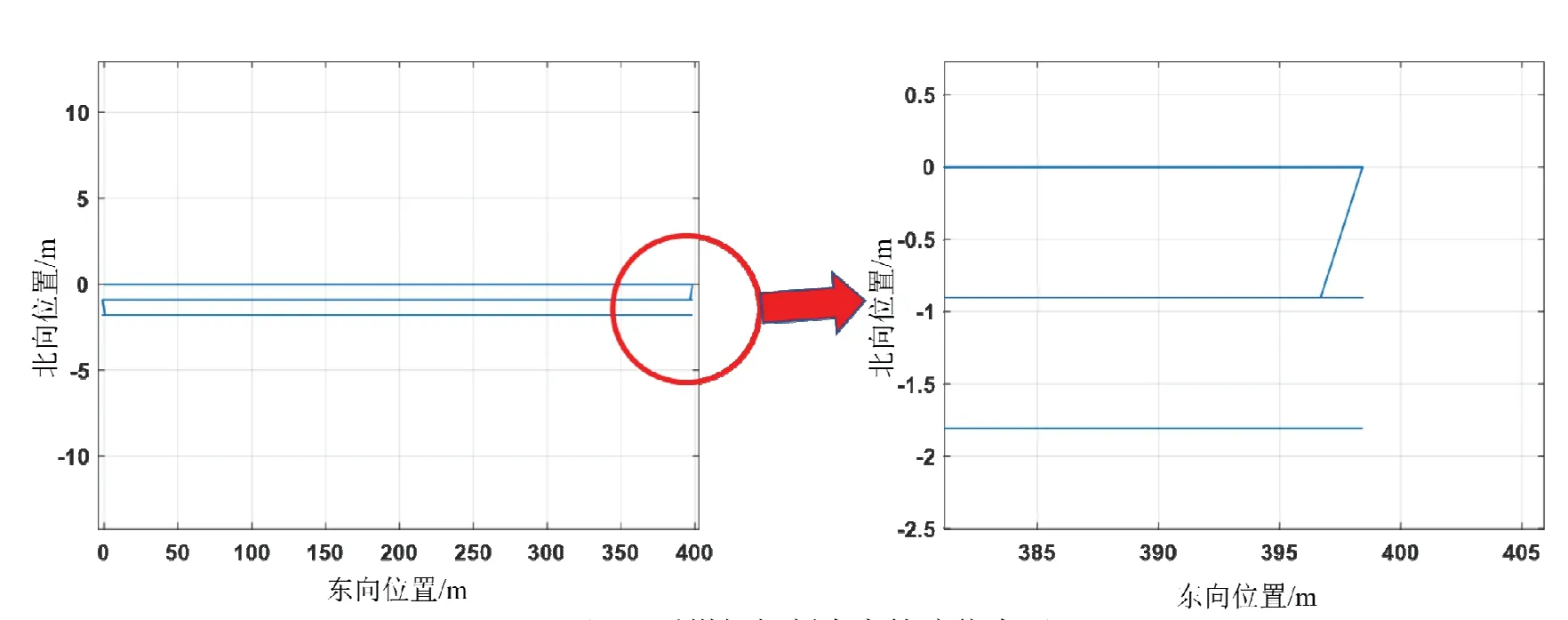
圖9 采煤機切割真實軌跡仿真圖Fig.9 Simulation diagram of the real trajectory of shearer cutting

3.2 雙層神經網絡模型參數辨識精度分析

為驗證雙層神經網絡模型參數辨識的正確率和辨識精度。仿真4組不同的采煤機完整開采過程的慣導/里程計輸出，并且根據切割狀態對數據進行分割，共分成4種不同工作模式下的11種噪聲模型，將各類模型下的慣導/里程計輸出標準差、方差、最大值和極差作為數據并添加多分類模型標簽進行依次訓練。

針對訓練好的雙層神經網絡，重新仿真4組完整采煤機開采的慣導和里程計輸出作為測試集并且根據采煤機的實際工作狀態添加相應模型分類標簽進行識別，將識別結果和添加的標簽進行對比，對比結果如表2所示。本文所提出的算法在模型切換時達到98%以上的識別率，相較于僅通過單層網絡辨識提高了12%以上的識別準確率，因此通過雙層辨識神經網絡有效提高了系統的辨識精度。

表2 算法的辨識精度對比Tab.2 Comparison of the identification accuracy of algorithms

3.3 改進變結構多模型定位精度分析

將訓練好的雙層神經網絡用于變結構多模型算法的模型參數辨識。為了驗證算法的實際融合效果，與傳統的交互多模型算法（Interacting Multiple Model,IMM）進行對比。根據仿真所設計的采煤機運動狀態，設計了多分類模型下慣導/里程計的噪聲模型參數，構建了多分類模型庫，如表3所示。每個多分類模型中設計了具體模型參數，分別對應變結構多模型算法中設計的4個濾波器噪聲信息。

表3 多分類模型庫設計Tab.3 Design of multi-classification model library

由于井下里程計受振動的影響較小，在采煤機運動方向上的誤差可以得到抑制，而航向完全基于陀螺儀輸出，陀螺系統噪聲的設置精度尤為重要，因此本文在多分類模型中構建了更多噪聲模型進行匹配。

圖10是不同算法和真值的軌跡對比，可以看出本文算法的軌跡精度顯著高于傳統IMM算法。圖11、圖12和圖13分別對比了兩種算法的東向位置誤差、北向位置誤差和航向角誤差。結合表4可以得到以下結論：IMM算法由于在較多模型集合的選擇中不能分配較為精準的權重，系統模型參數失配，導致濾波精度不高。相較于傳統算法，本文所提出算法憑借可靠的模型參數辨識，獲得了明顯的井下定位、定向精度提升。其中，本文所提算法的東向位置誤差均方差為1.15 m，北向位置誤差均方差為2.44 m；傳統IMM算法的東向位置誤差均方差為1.55 m；北向位置誤差均方差為4.54 m，有效抑制了由于振動噪聲導致的航向發散，航向精度提升42%，東向精度提升26%，北向精度提升46%，水平精度總體提升43%。另外，通過多組仿真，得到本文算法單次信息融合平均解算時間耗時為0.86 ms，傳統IMM算法的平均解算時間為2.75 ms。值得注意的是，采煤機在切割過程中航向誤差存在4處比較明顯的跳變，這是由于采煤機在切割到工作面端頭后進行斜切進刀過程中航向明顯變化導致。綜上，本文算法相較于傳統的IMM算法提高了井下采煤機在不同運動階段慣導/里程計的融合的定位精度，同時保證了解算效率。

圖10 不同算法的自主導航定位精度對比Fig.10 Comparison of different algorithms

圖11 東向位置誤差對比Fig.11 Comparison of east position error

圖12 北向位置誤差對比Fig.12 Comparison of north position error

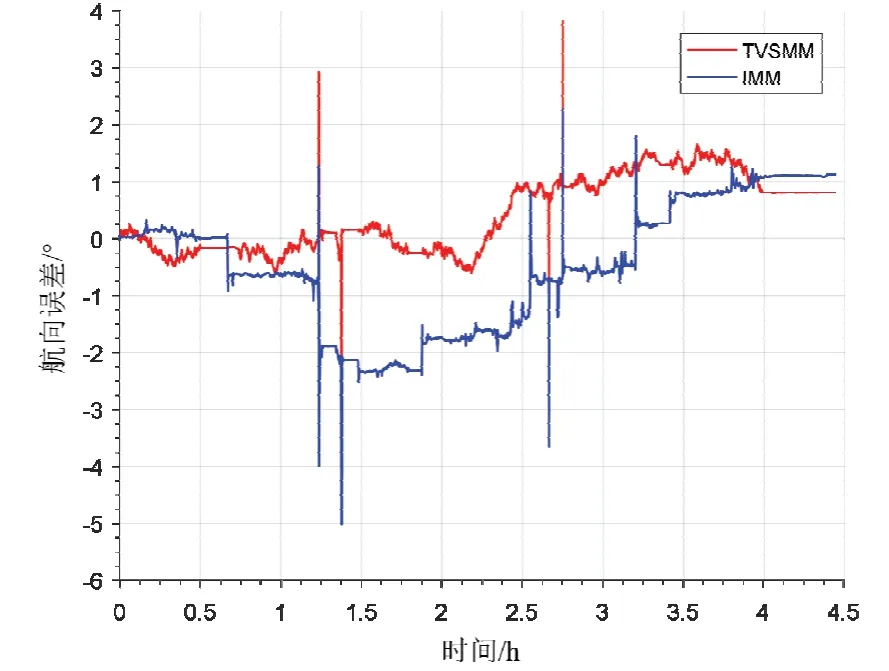
圖13 航向誤差對比Fig.13 Comparison of heading error

表4 算法定位精度對比Tab.4 Comparison of positioning accuracy of algorithms

4 結 論

本文針對井下采煤機采煤過程中的復雜運動狀態，基于高精度慣導系統和里程計設計了一種基于雙層神經網絡模型參數辨識的變結構多模型導航算法。利用慣導仿真數據針對不同運動模型的特征進行訓練，通過對數據分割與截取、特征建模、機器學習策略的研究，實現在采煤機運動模型在運動狀態變化時的精準切換。該算法不依賴于后驗概率，具有較快的模型切換的速度。通過變結構多模型與雙層神經網絡模型參數辨識算法的結合，解決了在GNSS拒止的復雜環境下時變系統的高精度定位問題。仿真結果表明，相較于傳統多模型導航算法，本文所提出算法能夠有效應對復雜、時變的井下振動環境，實現了實時、高精度的導航定位。