基于粗糙遺傳算法在打捆機齒輪箱故障診斷中的應用*
任彬,白東,謝虎,韓柏和,肖蘇偉
(1.石家莊鐵道大學機械工程學院,石家莊市,050043;2.農業農村部南京農業機械化研究所,南京市,210014;3.中國熱帶農業科學院橡膠研究所,海口市,571101)
0 引言
自走式連續作業打捆機作為一款新型的自動化、智能化農業機械產品,其關鍵部件齒輪箱長期處于高速、高載荷工作狀態下,易出現疲勞磨損、膠合、斷齒等機械故障。齒輪箱機械故障的發生會嚴重影響打捆機的正常作業,甚至延誤農時,造成經濟損失[1]。為了實現對不同故障類型的預測和防控,對齒輪箱實現故障診斷具有重要意義。
通過對振動信號時頻域分析提取故障特征參量,將特征參量作為評價指標進而實現故障診斷識別是一種常用的故障診斷方法[2-10]。其中Hou等[11]利用稀疏編碼和全局優化實現了滾動軸承弱故障特征的提取并進行故障診斷試驗,診斷率達到100%;Zappalá等[12]提出采用邊帶功率因數作為評價齒輪狀態的標準,有效的實現了故障自動診斷。但由于打捆機本身工作環境惡劣,振動信號成分復雜,同時常用故障特征參量冗雜,進一步提高了決策難度。因此,需要從眾多的故障特征參量中提取出對故障診斷決策有意義參量集合,并使得該集合盡可能小,以保證決策過程的便易性[13]。
粗糙集屬性約簡理論是波蘭學者Pawlak[14]提出的一種屬性約簡理論,婁玉華[15]利用粗糙集理論對提升機復合故障診斷決策表進行約簡獲得決策規則,通過試驗證明該規則集能有效診斷提升機故障;劉慧玲等[16]結合粗糙集和神經網絡,通過差別矩陣實現屬性約簡并利用神經網絡實現診斷,試驗結果表明該方法能有效實現故障診斷并提高診斷效率。經典粗糙集屬性約簡主要采用求核集的方式進行約簡[17-20],由于屬性約簡屬于NP問題,算法在決策表數據量大、屬性集較多時效率低下。
綜上所述,針對打捆機齒輪箱故障參量選取困難問題,采用粗糙集作為約簡理論,并通過自適應遺傳算法提高屬性約簡效率,得到最簡故障特征參量集和決策規則表,并根據決策規則表實現故障診斷,本文利用打捆機齒輪箱振動信號對該方法進行試驗驗證分析。
1 粗糙遺傳算法基本理論
屬性約簡是指在保持分類能力不變的情況下實現對冗余信息的剔除,即利用盡可能少的條件屬性實現對決策屬性的判斷。當前屬性約簡主要利用粗糙集理論實現數據信息的約簡,通過建立決策系統,利用不可分辨關系和正域等概念,遍歷式的對不同的屬性進行判斷分析,剔除其中的非必要屬性[21-24]。傳統約簡算法效率低,對先驗信息依賴性大,遺傳算法[25-26]作為一種啟發式智能算法能有效提高約簡效率,且無需先驗信息。利用遺傳算法實現屬性約簡,將決策屬性對條件屬性的依賴度作為遺傳算法的適應度函數,將條件屬性的不同組合作為遺傳種群,通過選擇交叉變異求得對決策屬性最重要的條件屬性,即最簡屬性集。
1.1 初始決策表建立
在利用屬性約簡實現故障特征參量的選取過程中,首先需要針對不同故障實例提取故障特征參量,并利用故障特征值建立初始決策表,決策表形式如表1所示。表1中U為論域,X1,X2…Xm為論域中的實例,Ci(Xj)為實例Xj的條件屬性Ci的值,D(Xj)為實例Xj的決策屬性值。

表1 決策表Tab.1 Table of decision
粗糙集理論只能處理離散的數據集,齒輪箱故障特征參數均為連續的數據值,因此需要對數據集實現離散化處理。為保證在決策屬性分類能力不變的條件下使斷點盡可能少,本文為采用SNS(Semi Naive Scaler)算法實現屬性集的離散化[27]。SNS算法是NS算法的改進,是對NS算法求得的斷點進一步刪減,去除冗余的過程。
NS算法首先選取連續屬性C,論域U中X的屬性C值為C(X),U中實例按C(X)的大小進行排列。從上到下掃描全域,尋找斷點。若存在條件C(Xi)≠C(Xi+1),且D(Xi)≠D(Xi+1),則認為該處存在斷點pi=[C(Xi)+C(Xi+1)]/2。
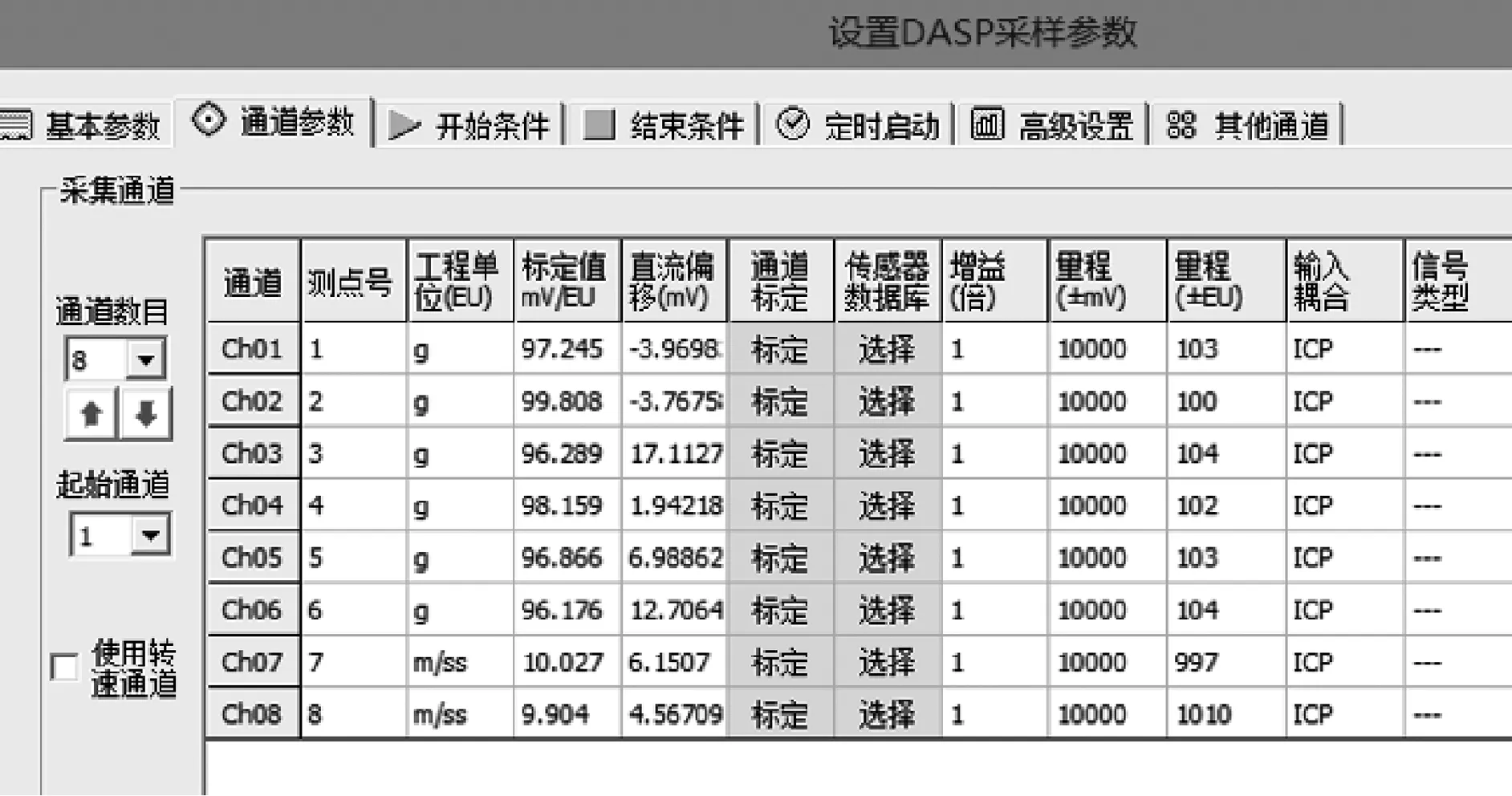
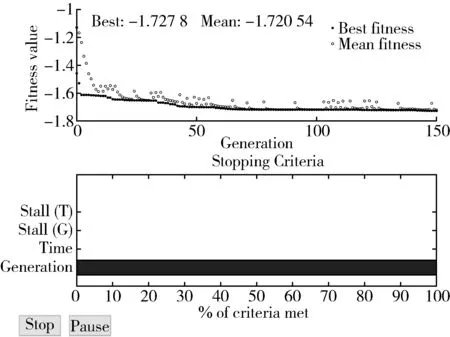
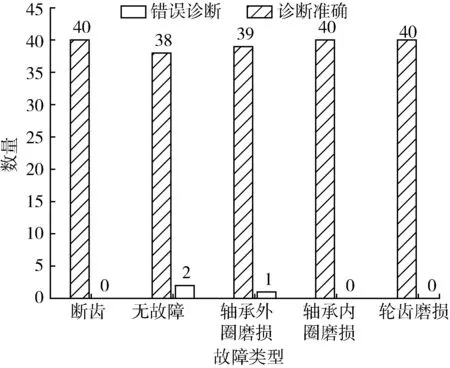
NS算法僅考慮單個的連續屬性,因此斷點較多,存在大量冗余。SNS算法針對NS算法得到的斷點分別進行討論,減少斷點數量。針對決策表中屬性C的某一斷點pi,首先將U中實例按C(X)的大小進行排列,存在i使得C(Xi) 圖1 SNS斷點法流程圖Fig.1 SNS breakpoint method flowchart 完成初始決策表的建立后,利用自適應遺傳算法對決策表進行屬性約簡,算法流程如圖2所示。 圖2 遺傳算法Fig.2 Genetic algorithm 基于自適應遺傳算法的屬性約簡具體過程如下。 Step1:初始化種群。首先由算法隨機生成多個染色體長度為L的二進制個體,個體的L條染色體分別代表初始決策表中的L個屬性。若某染色體編碼為1,則該染色體對應的屬性保留,否則去除該屬性。對于條件屬性為C={C1,C2,C3…C12}的決策系統,隨機生成某一個個體{110000100110}代表由C1、C2、C7、C10、C11組成的屬性集個體。 Step2:設置適應度函數。適應度函數是評價種群中個體優劣的關鍵,在利用遺傳算法實現屬性約簡的過程中,要求決策屬性對約簡后的條件屬性集依賴度最大,同時保證約簡后條件屬性集最小。設適應度函數 (1) (2) 式中:L——染色體長度; Lr——染色體中各非零數數量值,約簡后的屬性集中包含的屬性越多,則Lr的值越大,適應度F越低; γC(D)——決策屬性D對條件屬性C的依賴度,即條件屬性集的重要程度[28]; POSC(D)——D的C正域。 Step3:設置迭代終止條件。(1)達到設定的最大迭代次數。(2)迭代過程中每次適應度提高低于設定閾值。若遺傳算法滿足以上終止條件,則輸出當前種群中適應度最高的個體作為最優解。 Step4:選擇、交叉和變異。對種群個體的選擇采用輪盤賭博的方式,首先根據適應度的大小設定各個體的被選擇概率,使適應度函數值較大的個體被選中概率更大,然后根據輪盤賭博的方式在初始種群中選取交叉、變異的候選個體。 交叉算子是算法的核心部分,如圖3(a)所示。對種群中的個體成對隨機匹配,匹配到的父代個體隨機選擇一個交叉區域,交叉區域長度不能大于等于染色體長度L。被選區域以交叉概率pc進行交叉變換。 (a)交叉示意圖 變異是對種群中的個體染色體進行取反操作,對于候選變異個體,按照均勻分布隨機產生變異點,按變異概率pm對該染色體進行取反操作,如圖3(b)所示。 遺傳算法中交叉和變異概率pc和pm對算法尋優結果有著較大影響,標準遺傳算法采用靜態的pc和pm值。根據算法原理可知,若pc值太大,算法會較快產生新個體,但適應度較高的個體會被破壞,該值太小會導致進化速度太慢;pm值太大,算法收斂速度會變慢,該值太小會使新個體減少,降低種群多樣性[29]。基于該問題,Cao等[30]提出一種自適應遺傳算法,該算法根據每個個體的適應度值大小,對pc和pm的取值給出了相關計算公式。 (3) (4) 式中:Fmax——種群最大適應度值; Favg——種群平均適應度; F′——發生交叉的兩個體中適應度值較高的值; F″——發生變異的個體的適應度值; C1、C2、C3、C4——大于0小于1的參數。 Step 5:通過選擇、交叉和變異產生新的子代種群,根據最優保存策略[31],取父代種群中的最優個體直接復制到子代種群,代替子代中適應度最低的個體,同時保證種群大小不變。 Step 6:對新的子代種群重復步驟4和步驟5,直到種群滿足迭代終止條件。 遺傳算法的每一次迭代都使得種群向著適應度更高的方向演變,經過數次的迭代后便可以得到優良的后代種群。通過遺傳算法求得條件屬性中對決策屬性最重要的最簡屬性集,根據式(1)可知,該集合即對故障最敏感的最小故障特征參量集。 本文所選試驗對象為研發的自走式稻麥秸稈收割打捆機樣機,如圖4所示。主要針對其齒輪箱的振動信號進行采集工作,在本次采集工作中自走式打捆機處于空載狀態,分別采集3個不同轉速區間的振動信號。現場試驗分別采集了齒輪箱斷齒、齒輪磨損、正常齒輪、軸承內圈及外圈磨損的故障信號。信號采集硬件設備選用INV982X加速度傳感器和INV3810CT型采集儀,軟件為DASP信號采集和實時分析系統。圖5為打捆機齒輪箱上加速度傳感器的布置位置,傳感器通過采集儀進行驅動,并由采集儀存儲采集信號輸送給上位機,采集儀通過上位機的DASP軟件進行設置,設置界面如圖6所示。 圖4 自走式稻麥秸稈切割打捆機樣機Fig.4 Prototype of self-propelled straw baler 圖5 打捆機齒輪箱振動信號采集Fig.5 Acquisition of vibration signals for gearbox 圖6 DASP采集儀設置界面Fig.6 DASP collector setting interface 完成數據的采集和整理后,選取同一工作狀態下的不同故障類型振動信號作為被診斷信號,并分別選取多組信號進行故障特征參量值的提取。對不同故障類型信號各取50組提取特征參量,選其中3組作為約簡數據,40組作為測試數據。時域特征分別選取均值、最大值、峰值、有效值、均方根值、方根幅值、歪度、峭度、裕度及峭度指標,頻域特征參量選取功率重心及功率譜分散程度。 完成故障特征參量的計算,將各組振動信號的故障特征參量作為初始決策表的條件屬性C1~C12,齒輪箱故障狀態作為決策屬性D,其中數字1代表斷齒故障,2代表正常齒輪,3代表軸承外圈磨損故障,4代表內圈磨損,5代表齒輪磨損故障。為了便于約簡處理,采用SNS算法對初始決策表進行離散化,得到離散決策表如表2所示。 表2 離散后的故障特征決策表Tab.2 Decision table of fault feature is discrete 完成決策表的離散后,利用遺傳算法對條件屬性中的冗余屬性進行約簡。首先初始化遺傳種群,并設置適應度函數式(1),并設置算法迭代的終止條件為:(1)達到最大迭代次數,本文設置最大迭代次數為150次;(2)迭代過程中連續15次迭代中適應度提高為0。 完成種群的建立和適應度的設置后,采用輪盤賭博的方式隨機選取個體,進行交叉和變異,進而產生新的個體。對新產生的個體分別計算適應度值,并依據最優保存策略將其中適應度高的個體復制給下一代,算法迭代過程如圖7所示。算法中遺傳算法向目標值最小方向尋優,因此適應度函數設為負值。從圖7可以看出,最佳適應度值以及平均適應度值在迭代中不斷提高。 圖7 遺傳算法迭代過程Fig.7 Iterative process of genetic algorithm 遺傳算法經過數次的迭代,得到最優解為{000001101000},則最簡決策屬性集為{C6,C7,C9}。表2中條件屬性C1~C12經過約簡僅保留{C6,C7,C9}3項屬性,并對表中3項屬性及決策屬性完全相同的實例進行剔除,得到決策規則表,作為故障診斷知識庫,如表3所示。 根據決策表3,故障特征參量由12項約簡為3項,若求得某振動信號的方根幅值、歪度和裕度離散集為{110},則診斷齒輪發生輪齒斷齒,離散集為{011}或{001}時,判斷齒輪箱發生輪齒磨損。 表3 決策規則表Tab.3 Parameters of decision rule 屬性約簡得到的最優解并非唯一解,遺傳算法每次尋優結果均不唯一,不同求解結果理論上不影響最終診斷效果。例如:利用遺傳算法再次重復上述約簡試驗,可以求得新的最簡特征參量集{C1,C7,C9},該屬性集同樣可以作為故障診斷知識庫。 為驗證基于粗糙集和遺傳算法屬性約簡得到的決策規則表的有效性,利用MATLAB對決策規則表進行驗證試驗。對每種故障類型分別選取40組數據作為故障實例,診斷數據分別提取均值、方根幅值、歪度及裕度4項故障特征。為驗證該方法得到的不同決策規則表在故障診斷中具有普適性,設置{方根幅值,歪度,裕度}以及{均值,歪度,裕度}兩組決策規則分別進行故障診斷,檢驗診斷結果是否準確。 圖8為故障診斷結果,通過圖8可以看出,基于屬性集{C6,C7,C9}以及{C1,C7,C9}知識庫的診斷過程中,分別存在3例和4例的誤判。對于診斷過程中的誤判,考慮在進行屬性約簡過程中所取不同故障類型的信號組數太少,最終得到的決策表知識庫不完整,導致診斷過程中產生誤判。 因此在原試驗基礎上,將約簡信號組數從3組增加到6組,保持試驗參數不變,重復上述試驗,得到診斷結果如圖9所示。從圖9中可以看出,基于屬性集{C6,C7,C9}和{C1,C7,C9}的新決策規則表的診斷率均達到100%,證明該方法能準確有效地判斷打捆機齒輪箱故障的發生和類型。 (a)基于3組信號的{C6,C7,C9}屬性集 (a)基于6組信號的{C6,C7,C9}屬性集 通過上述對自走式打捆機齒輪箱故障診斷試驗,證明了基于粗糙遺傳算法的故障診斷方法在打捆機齒輪箱故障診斷中的有效性,利用約簡得到的決策表不僅能判斷故障是否發生,并且能準確地診斷齒輪箱的故障類型。 1)本文針對打捆機齒輪箱故障診斷過程中故障特征參量多的問題,采用了粗糙集理論實現特征參量集的約簡,并根據約簡后得到的決策表建立了診斷規則,實現故障診斷。 2)傳統粗糙集約簡方法在處理大型數據時存在效率低、依賴先驗信息等問題,本文采用自適應遺傳算法對屬性集進行了約簡,有效提高了算法運行效率且無需先驗信息。 3)分別對輪齒斷裂、磨損、軸承內外圈磨損等故障狀態下的打捆機齒輪箱進行了信號采集,并將粗糙遺傳算法應用于故障信號的診斷,對算法的有效性進行驗證分析。分析結果表明:基于粗糙遺傳算法的故障診斷方法有效實現了打捆機齒輪箱故障特征參量的約簡,將初始決策表的12項故障特征參量約簡為3項。分別利用約簡得到的2組決策規則進行了故障診斷,診斷率均為100%。 4)該方法能夠在無先驗信息的條件下實現了屬性約簡,獲取了最簡故障特征參量,特征集的簡約性和對故障的敏感性符合監測需求,為齒輪箱故障監測提供科學的監測指標,同時基于決策規則表的故障知識庫能準確完成故障診斷,有效提高了打捆機的可靠性。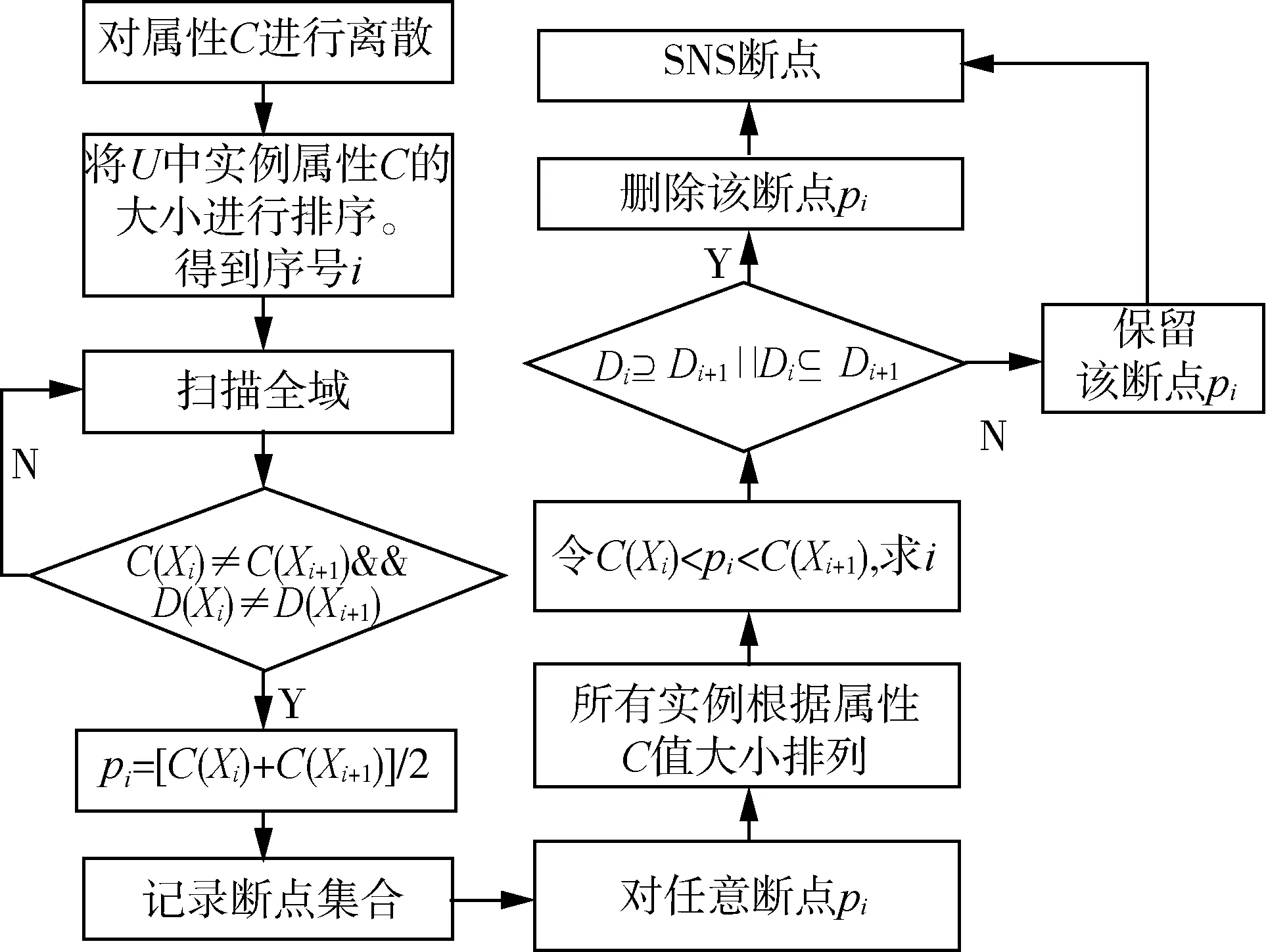
1.2 基于自適應遺傳算法的屬性約簡
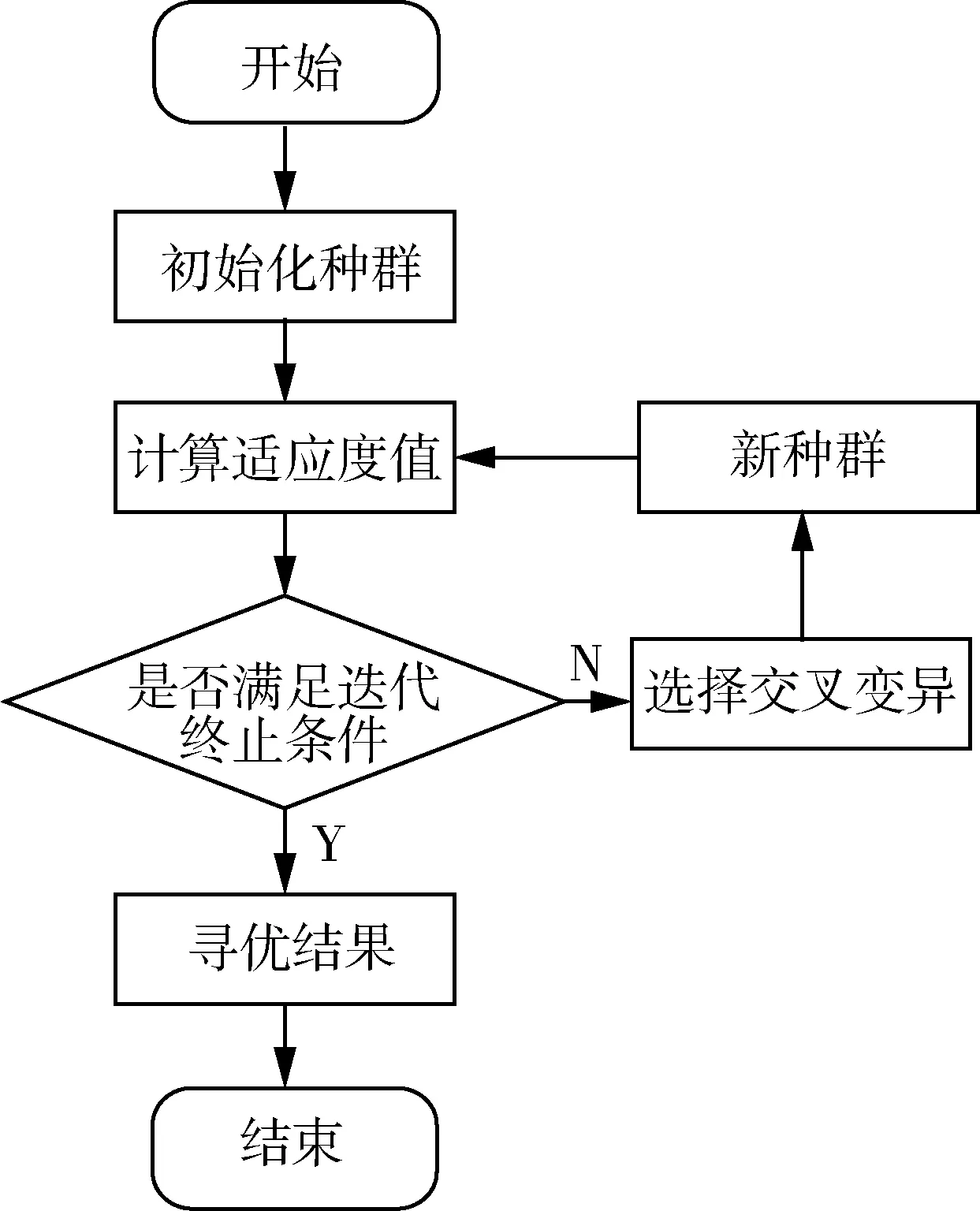

2 打捆機齒輪箱故障診斷試驗
2.1 建立初始決策表


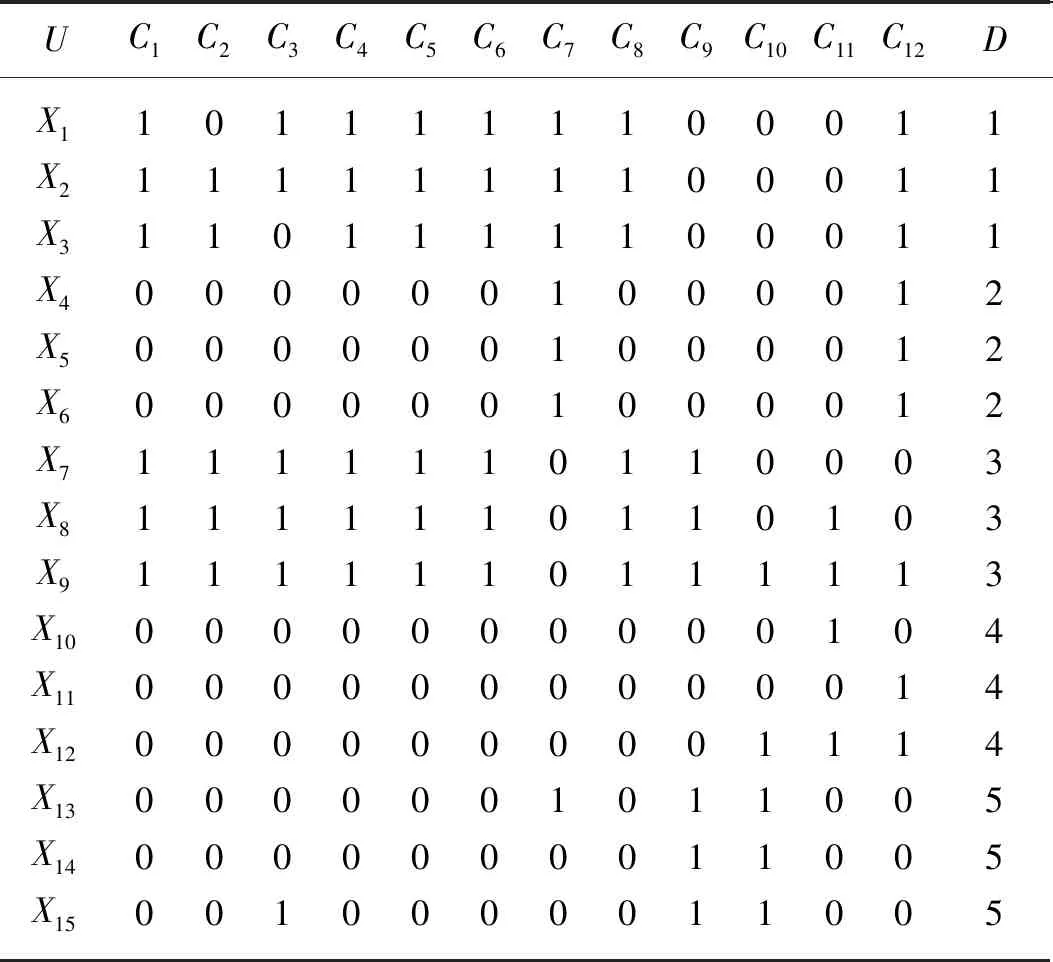
2.2 決策表屬性約簡

2.3 決策規則驗證

3 結論

