基于勢能信息熵的黃土小流域溝谷網絡演化特征研究

趙 衛 東，周 文 怡，馬 雷，田 劍，王 淑 琴

(合肥工業大學資源與環境工程學院，安徽 合肥 230009)

0 引言

受內外應力等因素的長期作用，黃土高原地貌演化過程非常復雜[1-3]。溝谷網絡是黃土高原流域地貌的主要侵蝕產沙區[4]和最主要的產沙運移通道，也是黃土小流域地貌系統研究中重要的地形因子，溝谷網絡的演化過程很大程度上能反映其所屬流域的地貌演化特征，因此，溝谷網絡演化過程研究對探索流域地貌演化特征具有重要意義。以往溝谷網絡研究多以黃土高原小流域為基本單元，借助室內模擬實驗[5-8]、野外實際測量等數據，采用D8算法、多流向算法等提取溝谷網絡[9-11]，通過特征指標[12-15]對小流域地貌系統內部的溝谷網絡形態等演化特征進行研究[16，17]，流域內部溝谷網絡的演化過程與整個流域系統地貌演化過程的相互作用機制未得到有效揭示，有待深入研究。

在一般系統論中，通常用有序和無序描述系統及系統內部各要素之間的狀態和關系[18，19]。其中，有序在自然界和人類社會中存在靜態有序(平衡結構)和動態有序(非平衡結構)[20]兩種形式，現有研究表明，一個開放系統(如生物有機體等開放系統[21])可成為不斷趨于有序化的系統。龔俊豪利用定量與定性相結合的方法，研究黃土高原小流域地貌系統的有序化演化機理，發現在以侵蝕為主的流域地貌系統的演化過程中，流域內部坡向和河網呈有序演化狀態，初步闡明了以侵蝕為主的小流域地貌系統的演化過程是一個不斷趨于有序化的過程[20]。然而，該研究僅從總體上對系統的河網有序性演化過程進行定性描述，未定量揭示河網具體的有序演化過程和有序程度。

熵能在一定程度上反映系統內部分子運動及能量的變化。近年來，部分學者在前人關于地貌熵研究成果[22-25]的基礎上提出了新的地貌熵概念及計算方法。例如:Zhao等提出流域地貌熵的概念及計算方法，認為其與地貌的侵蝕發育緊密相關，并將流域地貌熵成功應用于黃土高原人工降雨小流域模擬試驗中[26]；姜瓊在流域地貌系統和信息熵概念的基礎上提出流域地貌系統勢能信息熵的概念及計算方法，用于反映流域地貌系統內部勢能分布的混亂程度，并對其蘊含的地貌演化意義進行初步研究，證明利用勢能信息熵對流域地貌系統的地貌演化過程進行研究切實可行[27]。流域地貌系統作為開放的自然系統，其在演化過程中不斷與外界產生物質交換和能量轉換。例如，降雨通過入滲或地表徑流進入流域地貌系統，降雨侵蝕會導致地表高程發生變化，從而使系統內部勢能發生相應變化，因此，勢能信息熵反映的系統內部勢能在空間分布上的混亂程度可在一定程度上有效反映流域地貌系統內部的地貌侵蝕和演化發育特征。為此，本文擬以小流域地貌系統及其溝谷網絡為研究對象，從勢能信息熵角度定量研究流域地貌系統內部溝谷網絡的有序演化過程。

1 數據與研究方法

1.1 研究數據

本文DEM數據來自人工模擬降雨條件下室內黃土侵蝕試驗，模擬的黃土小流域長9.1 m，寬5.8 m，周長23.3 m，平均高差2.57 m，平均坡度15°；試驗用土為陜西省咸陽市楊凌區附近的黑塿土，建模時分層填土，層層夯實，實測土體平均密度為1.39 g/cm3。利用近景數字攝影測量方法，獲得該人工小流域地貌系統9期DEM數據(圖1)，相鄰兩期DEM的拍攝時間間隔為一星期左右，其中第1期為首次人工降雨前的初始地形，數據柵格單元大小為10 mm。該試驗共經歷23場不同強度、歷時的降雨，總歷時兩個多月，9個侵蝕演變階段的降雨參數如表1所示。

表1 室內人工降雨試驗的降雨參數(根據文獻[28]修改)Table 1 Parameters of indoor artificial simulated rainfall test (modified according to literature [28])

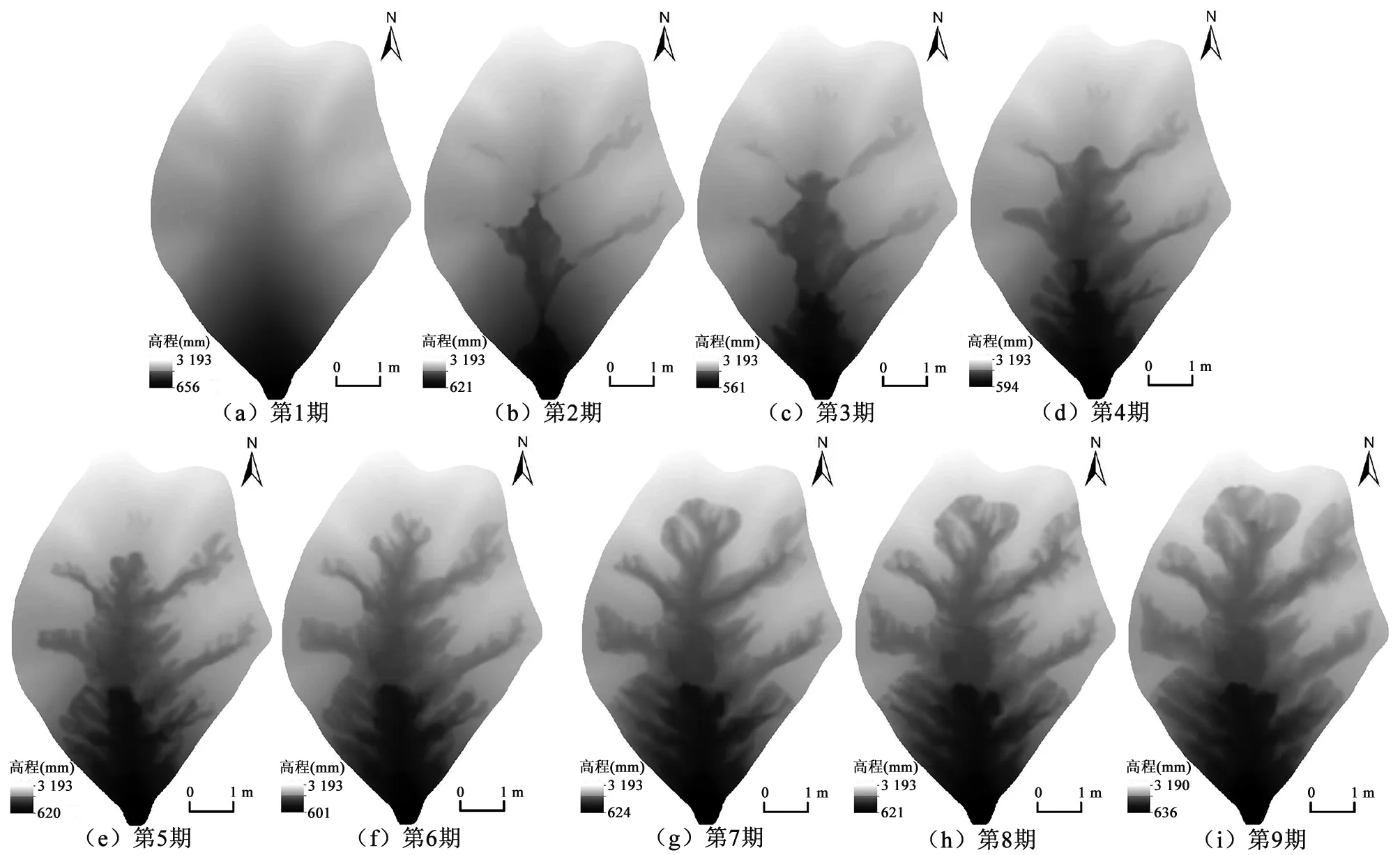
圖1 室內人工降雨模擬的9期DEMFig.1 9-phase DEM of indoor artificial rainfall simulation

1.2 溝谷網絡及子流域提取方法

首先，對9期DEM進行填洼處理，得到無洼地DEM；然后，利用D8算法計算水流方向，并根據水流方向數據得到每個單元格的匯流累積量；當該匯流累積量大于地表產生匯流所需匯流累積量的臨界值時，該單元格就被識別為潛在水流路徑，這些水流路徑相互連接即構成整個溝谷網絡。因此，合理確定地表產生匯流所需匯流累積量的臨界值是準確提取溝谷網絡的關鍵。本文采用南學良等[29]提出的溝谷網絡密度二階導函數參數確定匯流累積量的臨界值，通過溝谷網絡密度與閾值之間的關系得到其冪函數擬合方程，進一步得到其二階導函數，能較好地排除閾值選取的主觀性。本文9期小流域溝谷網絡密度二階導函數曲線如圖2所示,可以看出，當匯流累積量閾值為8 000時，溝谷網絡密度二階導函數值趨近于0[30]。因此，本文取8 000為匯流累積量閾值，并在此基礎上對提取的溝谷網絡進行Shreve分級。

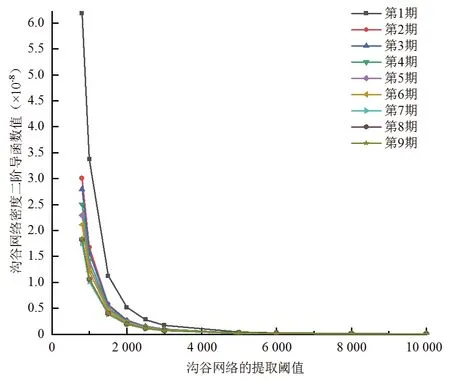
圖2 溝谷網絡密度二階導函數曲線Fig.2 Curves for second order derivative of valley network density

1.3 勢能信息熵計算方法

由于整個流域地貌系統的勢能難以直接計算，因此，基于DEM格網剖分技術將流域劃分為多個正方格網單元，后續流域地貌系統內部的勢能及勢能信息熵均基于上述剖分單元進行計算。由于本文流域地貌系統為室內人工模擬地貌系統，系統內部黃土密度均勻，因此不進行土層垂直方向上的剖分。流域地貌系統內部第i行和第j列剖分單元的勢能Epi，j計算公式為[27]:

(1)

式中:ρ為黃土密度(1.39 g/cm3)；g為重力加速度(10 N/kg)；d為格網單元尺寸(10 mm)；Hi,j為第i行第j列剖分單元相對于流域地貌系統出口最低點的高度(mm)。

假設某流域地貌系統內部共剖分出n個計算單元，利用式(1)可計算出每個單元的勢能，從而得到該流域地貌系統的最大和最小勢能，進而將系統勢能等間距劃分成N個勢能等級，則該流域地貌系統的勢能信息熵Hg計算公式為[27]:

(2)

式中:p(i)為單元i所屬的勢能等級在該流域中所有勢能等級中出現的概率。

由式(2)可知，流域地貌系統的勢能信息熵值與勢能等級的劃分緊密相關，勢能信息熵總體上隨勢能分級數的增加不斷減小，當勢能分級數達到足夠大時才能得到一個穩定勢能信息熵[27]。只有在最佳勢能分級數下，才能準確計算出流域地貌系統的唯一勢能信息熵。因此，本文取勢能信息熵的變化率為負萬分之一時對應的分級數為最佳分級數(4 915級)，由此計算勢能信息熵作為該流域地貌系統的唯一勢能信息熵，后續勢能信息熵均采用該分級數進行計算。

2 結果分析

2.1 基于Shreve分級的溝谷網絡演化特征

利用前述溝谷網絡提取方法提取9期DEM的溝谷網絡如圖3(彩圖見封2)所示，每條溝谷旁標注的數字為該溝谷所屬的Shreve級別。可以看出，9期DEM小流域溝谷網絡均具有典型的樹狀結構。為定量描述樹狀結構的有序性，本文提出以下溝谷網絡有序性程度判定規則:當溝谷網絡中存在的Shreve級別最多且主溝谷上各溝谷級別之間連續分布，即中間溝谷級別沒有缺失時，判定此時的溝谷網絡有序性最強；反之，如果溝谷級別有缺失，則判定其有序性較弱，溝谷級別缺失越多，有序性越差；當溝谷網絡的有序性達到最強后，如果其主溝谷的最大溝谷級別不斷減小，也判定其有序性受到破壞，有序性變弱。

從圖3可以看出，第1期DEM最大溝谷級別為第12級(溝谷總數為8個)，缺失級數為第4、第6、第7和第10級。由于該初始地形為尚未進行人工降雨的人工構筑地形，與自然條件下形成的溝谷網絡有明顯差異，根據前述溝谷網絡有序性強弱的判定規則，此時的溝谷網絡有序性最差。第2期DEM最大溝谷級別為第10級(溝谷總數為9個)，缺失第6級。經過第一次人工降雨后，人工構筑的溝谷網絡受降雨沖刷后逐步合并演化，使缺失的溝谷級別大幅減小，溝谷有序性大幅增強，初步具備自然形成的溝谷網絡形態。到第6期時，最大溝谷級別為第13級，與溝谷總數(13個)均達到最大值，且溝谷級別完整、連續，此時溝谷系統的有序性最強。

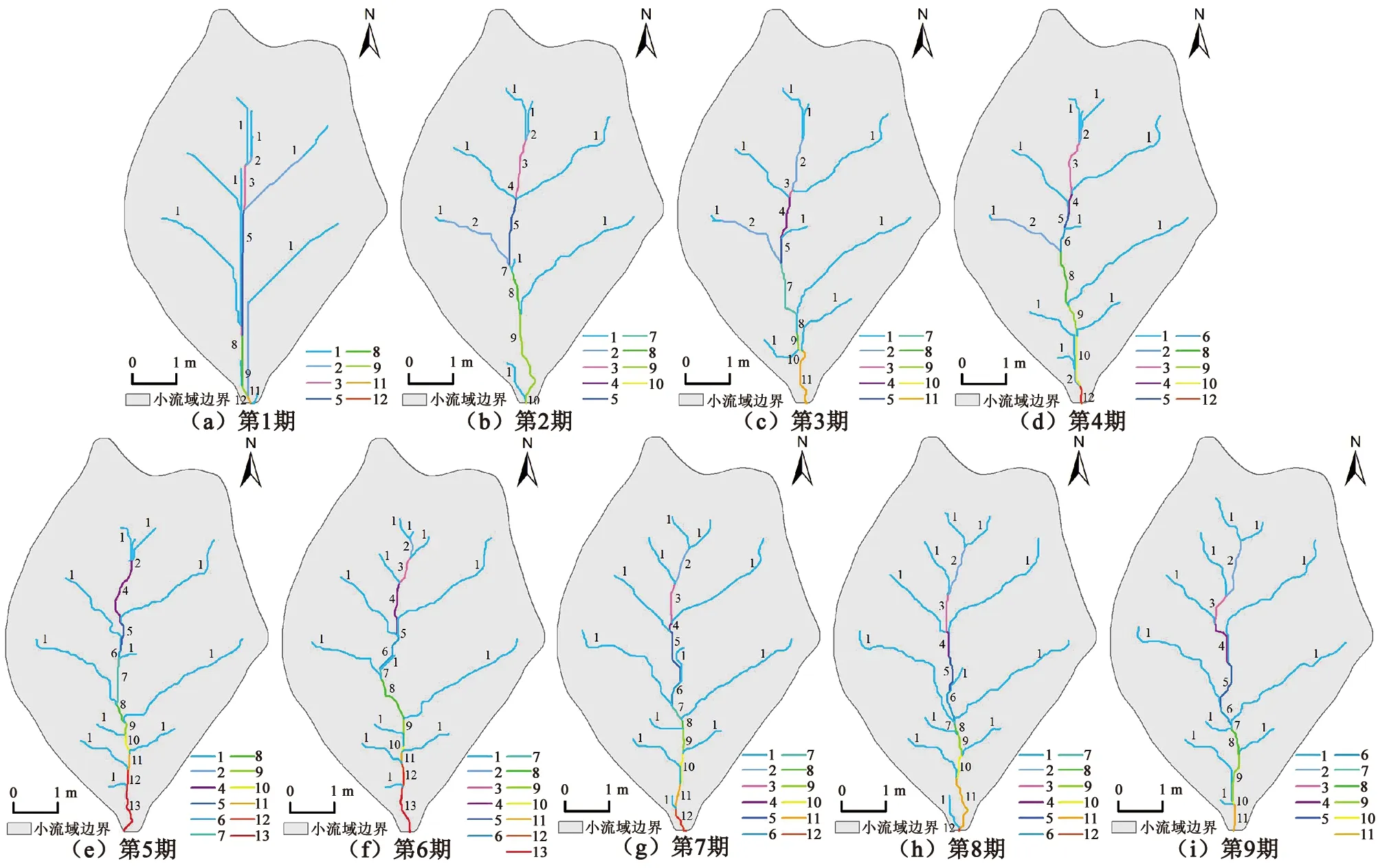
圖3 提取的溝谷網絡Fig.3 Extracted valley network

為進一步深入研究溝谷有序化演化過程，對9期DEM的溝谷級別總數和缺失數據進行統計(圖4)可知，從第1期到第6期溝谷級別總數總體不斷增加，主溝谷中缺失的溝谷級別整體不斷減少，溝谷網絡的有序化程度總體不斷增強。其中，在從第3期到第4期的演化過程中，溝谷級別總數沒變(均為10級)，而缺失溝谷的級別卻從1個增加到2個，表明該過程中溝谷網絡的有序性遭到破壞，可能是由于第4期的降雨歷時較長(是第3期的兩倍多)，導致流域出水口左側的黃土出現塌陷和溝谷深切形成新支溝，從而破壞了溝谷網絡的有序性。

從圖4可知，第1期到第6期曲線總體從左上角向右下角延伸，將該階段命名為第一階段；第6期到第9期曲線從右向左延伸，將該階段命名為第二階段。在溝谷網絡演化的第一階段，雖然在不同程度上存在溝谷級別缺失的情況，但溝谷網絡的最大級別數、級別總數不斷增加，缺失的溝谷級別逐漸被補滿，至第6期時溝谷級別總數達到最大(13級)，且中間無缺失的溝谷級別，因此，總體上看，在溝谷網絡演化的第一階段，整個溝谷網絡的有序演化程度不斷加強。在溝谷網絡演化的第二階段，除主溝谷外，其他溝谷均無支流匯入，整個溝谷網絡的溝谷級別完整，但主溝谷的最大溝谷級別數開始逐步減小，導致溝谷級別總數也同步減小，致使溝谷網絡的有序性被破壞，溝谷網絡的有序演化程度有所減弱。

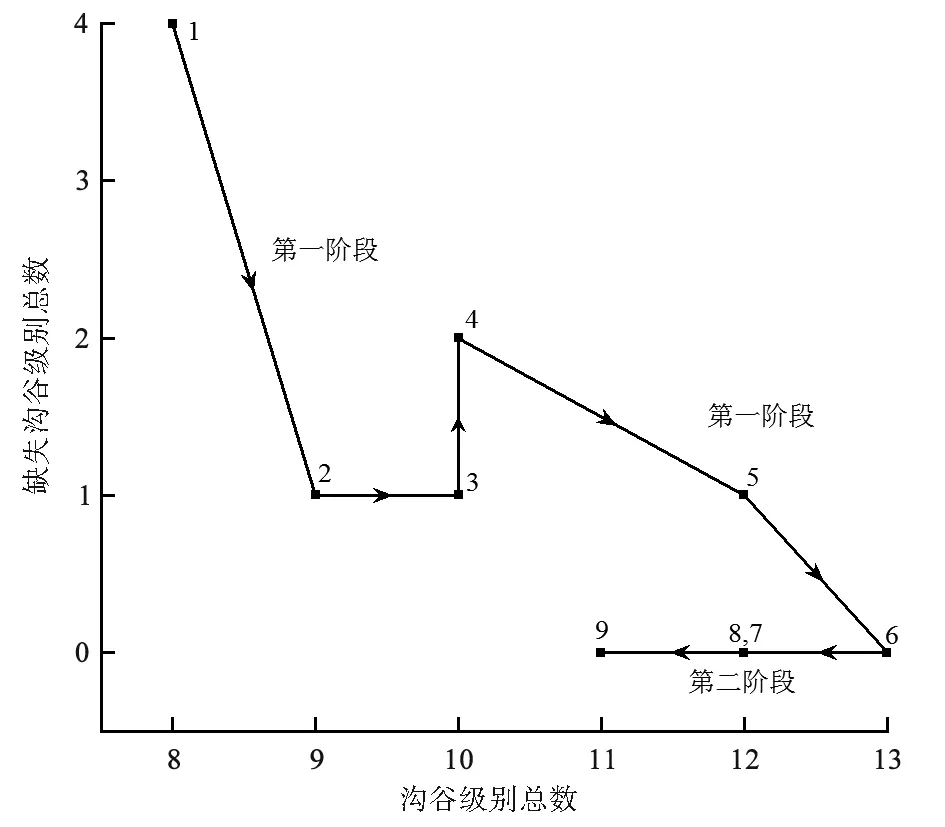
圖4 溝谷級別總數與缺失溝谷級別總數的變化關系Fig.4 Relationship between the total number of valley levels and the total number of missing valley levels

2.2 基于勢能信息熵的溝谷網絡演化特征

由整個流域地貌系統的勢能信息熵計算結果(圖5)可知，9期DEM的勢能信息熵均為負熵，且總體呈先遞減后小幅增加的態勢。根據文獻[27]，第1期到第6期為該小流域地貌演化的幼年期，流域地貌系統的勢能信息熵從最大值-7.993逐步減小到第6期時的最小值-8.194，為勢能信息熵的熵減過程；第6期到第9期為壯年期，勢能信息熵從最小值-8.194小幅增至-8.147，為勢能信息熵的熵增過程。根據一般系統論和熵變理論，開放系統的熵減過程為該系統有序化演化過程，熵越小，表明該系統的有序性越強，反之亦然。流域地貌系統是典型的開放系統，該系統在幼年期的地貌演化過程中有序化程度不斷增強，但壯年期的地貌演化過程中有序化程度有所減弱，該結論與2.1節中流域地貌系統的溝谷網絡有序演化過程完全一致。這表明，在以侵蝕為主的均質黃土流域地貌系統的演化過程中，地貌演化的幼年期是一個勢能信息熵的熵減過程，同時也是該系統內部溝谷網絡有序化程度不斷增強的過程；壯年期則是一個勢能信息熵的熵增過程，同時也是該系統內部溝谷網絡有序化程度不斷減弱的過程。在本文實驗條件下，流域地貌系統勢能信息熵的熵變規律及其內部溝谷網絡的有序化程度均對流域地貌系統的地貌發育階段具有良好的指示作用。

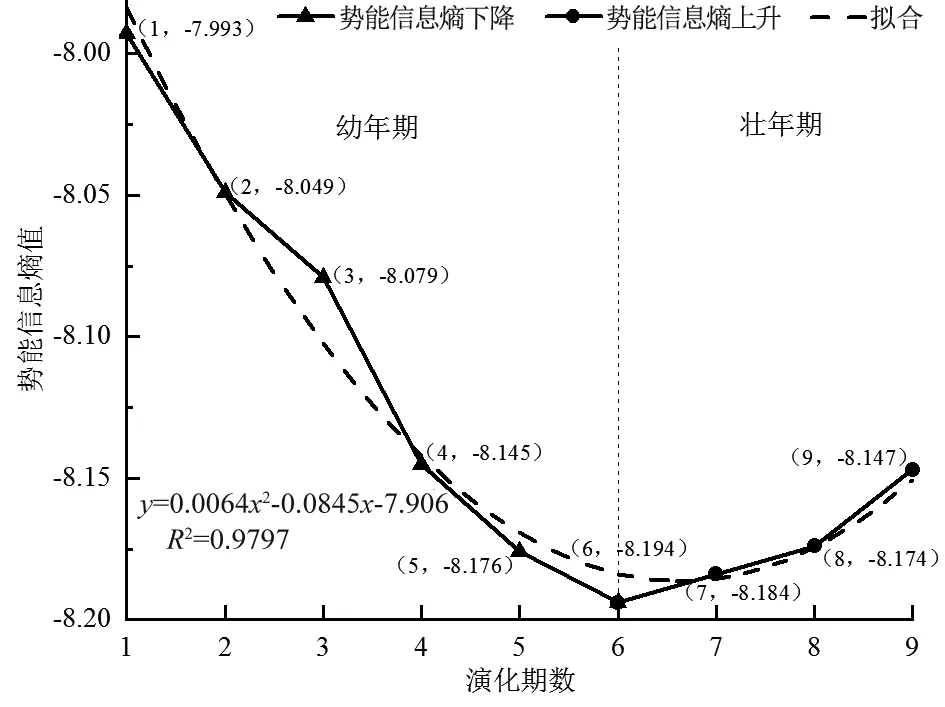
圖5 9期黃土小流域總的勢能信息熵值變化過程Fig.5 Changes of total PEIE values of small loess watershed in the 9 phases

3 結論與討論

本文基于室內模擬人工降雨試驗獲取的均質黃土小流域地貌演化過程中的9期DEM數據，探討了黃土小流域地貌系統內部的溝谷網絡和勢能信息熵的演化特征。首先，提出一種判別流域地貌系統內部溝谷網絡有序程度的新規則，該規則能對溝谷網絡的有序程度進行有效的定量表達。然后，計算整個流域系統的勢能信息熵，結果表明：以侵蝕為主的均質黃土流域地貌系統在地貌演化的幼年期是一個勢能信息熵的熵減過程，同時也是該系統內部溝谷網絡有序化程度不斷增強的過程；在地貌演化的壯年期則是一個勢能信息熵的熵增過程，同時也是該系統內部溝谷網絡有序化程度不斷減弱的過程。勢能信息熵的增減、溝谷網絡有序化程度的強弱均與流域地貌的發育階段相對應，因此，流域地貌系統勢能信息熵的熵變規律及其內部溝谷網絡的有序化程度均對流域地貌系統的地貌發育階段具有良好的指示作用。

本文僅探討了黃土小流域地貌系統演化過程中幼年期和壯年期早期的勢能信息熵和溝谷網絡的演化特征，之后的演化過程特征有待進一步深入研究。此外，后續室內模擬實驗中應充分考慮土層的非均質性、植被等對流域系統地貌演化過程的影響。