空間非合作目標未知構型重建質量評估方法
李榮華,李 恒,林婷婷,王 蒙
(1. 大連交通大學機械工程學院,大連 116028;2. 上海宇航系統工程研究所,上海 201109)
0 引 言
在軌服務技術和空間碎片清除技術是太空探測技術的重要組成部分,如何在復雜空間環境下有效保護空間軌道資源,進行衛星維修、壽命延長及垃圾清理是目前亟需解決的關鍵問題[1]。要解決上述問題,必須獲得空間非合作目標運動參數及三維形貌信息,并通過質量評估方法驗證三維形貌精度,只有符合精度要求,服務航天器才能接近目標航天器實施在軌服務[2]。
目前在對空間非合作目標進行三維形貌恢復時,重建方法主要分為兩種:第一種是采用序列圖像的重建方式[3-4]。第二種是采用激光雷達設備獲取精度較高的三維數據,再經過目標運動特性分析、點云預處理、點云配準、三維重建等技術手段,獲得三維模型[5-6]。激光雷達突破了傳統的成像概念和模式,具有極高速度分辨率、且工作距離長、受光照條件影響小,可以快速獲取目標某個視角的三維空間信息[7]。與傳統的幾何建模相比,基于激光雷達的三維模型重建方法更加精確、高效,應用領域也更加廣泛[8]。
三維重建完成后,重建點云是否可用于控制服務航天器對目標航天器進行在軌服務,三維模型是否可用于目標航天器的狀態和關鍵部位識別,進而引導平臺接近服務目標等,都是未知的[9]。可見,對重建結果進行質量評估是非常重要的環節。Javaheri等[10]通過選定的客觀質量指標與人類質量評估的相關性進行評價。陳鳳等[11]對基于序列圖像獲得的三維重建結果提出點云精度、重建目標識別完整性和吻合度等評估方法。Cheng等[12]提出一種雙目標卷積神經網絡,可以估計圖像的退化類型和質量評分。Arora等[13]提出一種模型中的圖像質量評估方法,包括水平和垂直質量評估以及對角線和反對角線質量評估的混合。于康龍等[14]基于結構相似度和尺度空間理論,提出一種針對超分辮率重建圖像的弱參考質量評價算法。田陽等[15]對三維重構誤差傳播機理進行分析,給出了三維重建誤差計算方法。文獻[16]從噪聲、密度、完整性、準確性等方面對采集的點云數據進行質量評價。陳西江等[17]將誤差橢球引入到點云精度分析中,重點分析了誤差橢球與點位協方差的關系。
上述評估方法多數都是針對圖像序列三維重建或有已知模型進行對比分析,而對于線陣激光雷達測量未知構型的空間非合作目標重建質量評估研究相對較少,還沒有統一的評判標準及評估方法。如何基于激光雷達測量的空間非合作目標未知構型三維重建結果建立有效而又簡便的質量評估體系,是亟需解決的關鍵問題。因此,本文提出空間非合作目標未知構型重建質量評估方法。該方法著重解決空間非合作目標未知構型重建質量評估問題,確保服務航天器能夠精確實施在軌服務。
1 重建質量評估流程
基于線陣激光雷達測量的空間非合作目標三維重建結果直接影響在軌服務質量。由于目標是非合作的,將無法利用重建模型與真實模型進行對比來驗證重建算法是否達到預期效果。因此,針對非合作目標三維重建結果,必須建立合理、完善的評估體系,確保在軌服務能夠順利進行。因此,本文從重建點云密度、重建幾何性質、重建表面完整度以及建立的多因素綜合評估對空間非合作目標重建結果進行分析,獲得對重建結果的滿意度,其流程如圖1所示。
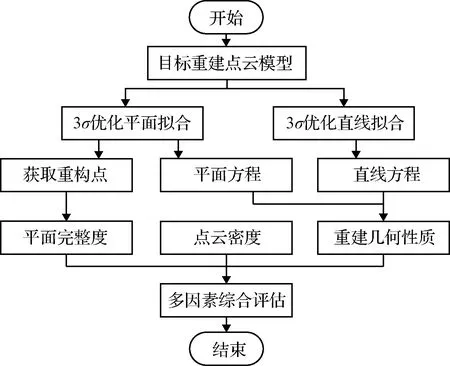
圖1 質量評估流程圖Fig.1 Quality assessment flowchart
2 3σ優化擬合
這里主要認定基于激光雷達測量獲得的重建點云模型表面多數為空間平面與直線,再結合人眼視覺特性判斷重建點云中的平面與直線位置,構建數學模型,即在指定表面或直線上選取一定數量特征點,利用這些特征點進行擬合;然后利用3σ法則不斷循環去除效果不好的數據點,優化擬合結果。
2.1 空間平面擬合
根據三維重建結果,選取模型平面點云數據(Xi,Yi,Zi),i=1,2,3,…,N,進行區域均勻采樣,獲得部分采樣點(xi,yi,zi),i=1,2,3,…,n。依據采樣點擬合出最優平面,使得每一個采樣點到平面的距離的平方和最小,其流程如圖2所示。

圖2 平面擬合流程圖Fig.2 Flow chart of plane fitting
平面方程的一般表達式為:
Ax+By+Cz+D=0,(D≠0)
(1)
兩邊除以D得到:
則有:
ajx+bjy+cjz+1=0,j=1,2,…,n
式中:
所有采樣點到平面距離的平方和為:
(2)
只有當S最小時,才能獲得最優平面,因此應滿足:
(3)
化簡整理:
采用克拉默法則求解線性方程組得到aj,bj,cj,即求得平面方程為:
ajx+bjy+cjz+1=0,j=1,2,…,n
(4)
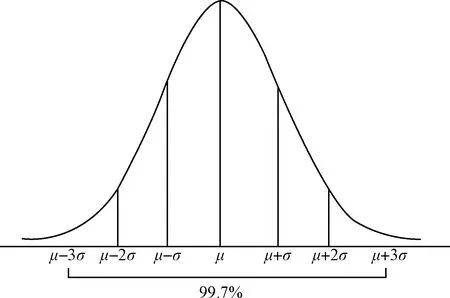
圖3 正態分布示意圖Fig.3 Schematic diagram of normal distribution
在圖3正態分布中,很容易發現:
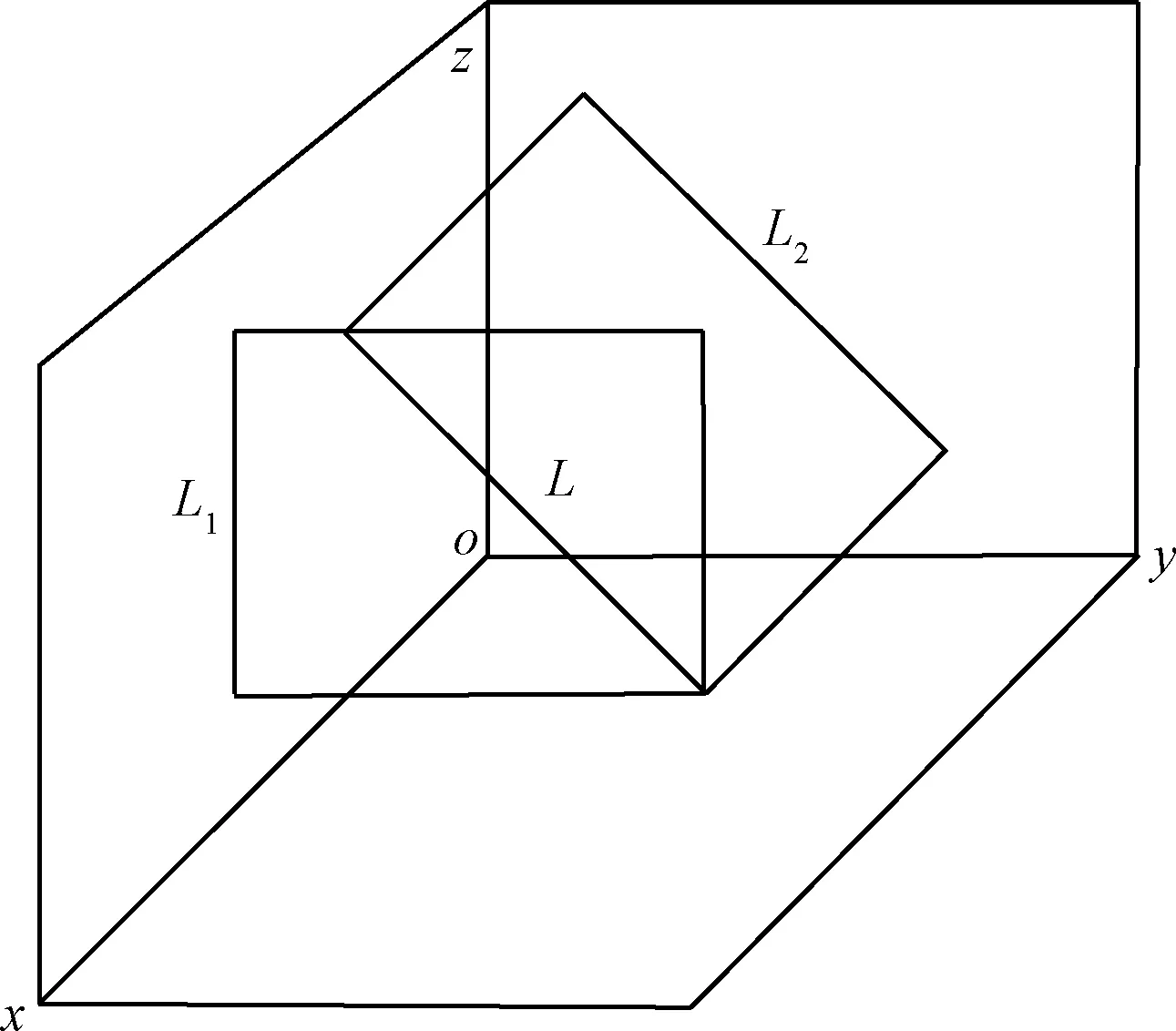
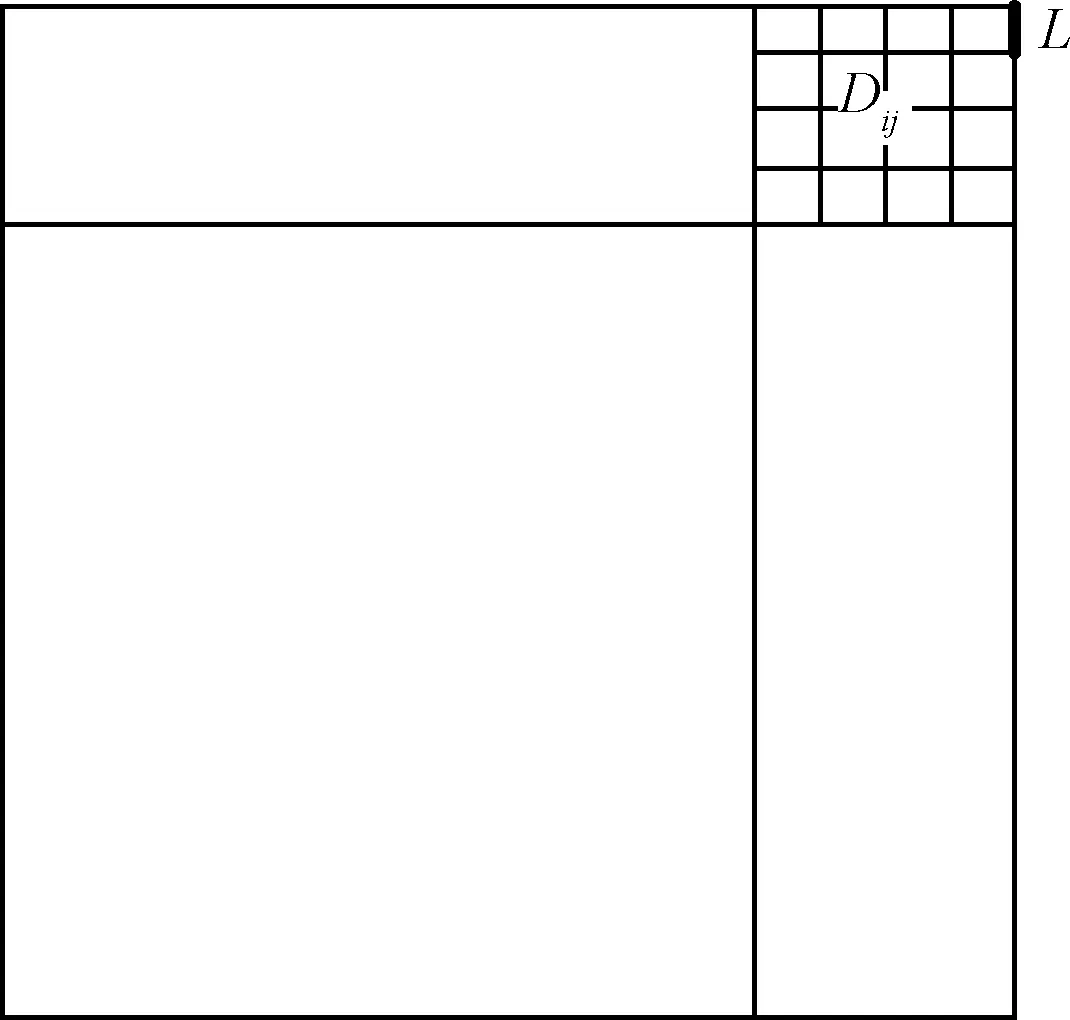
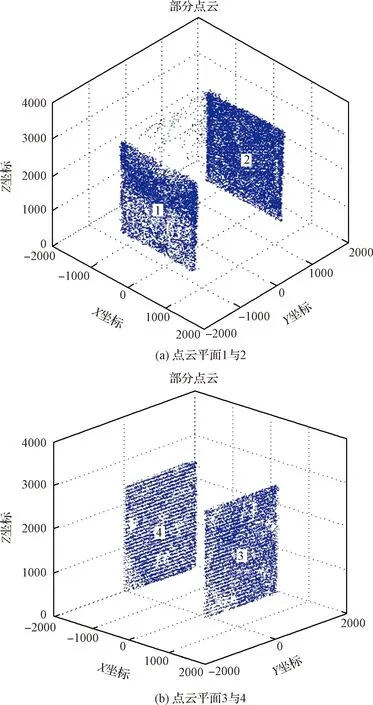
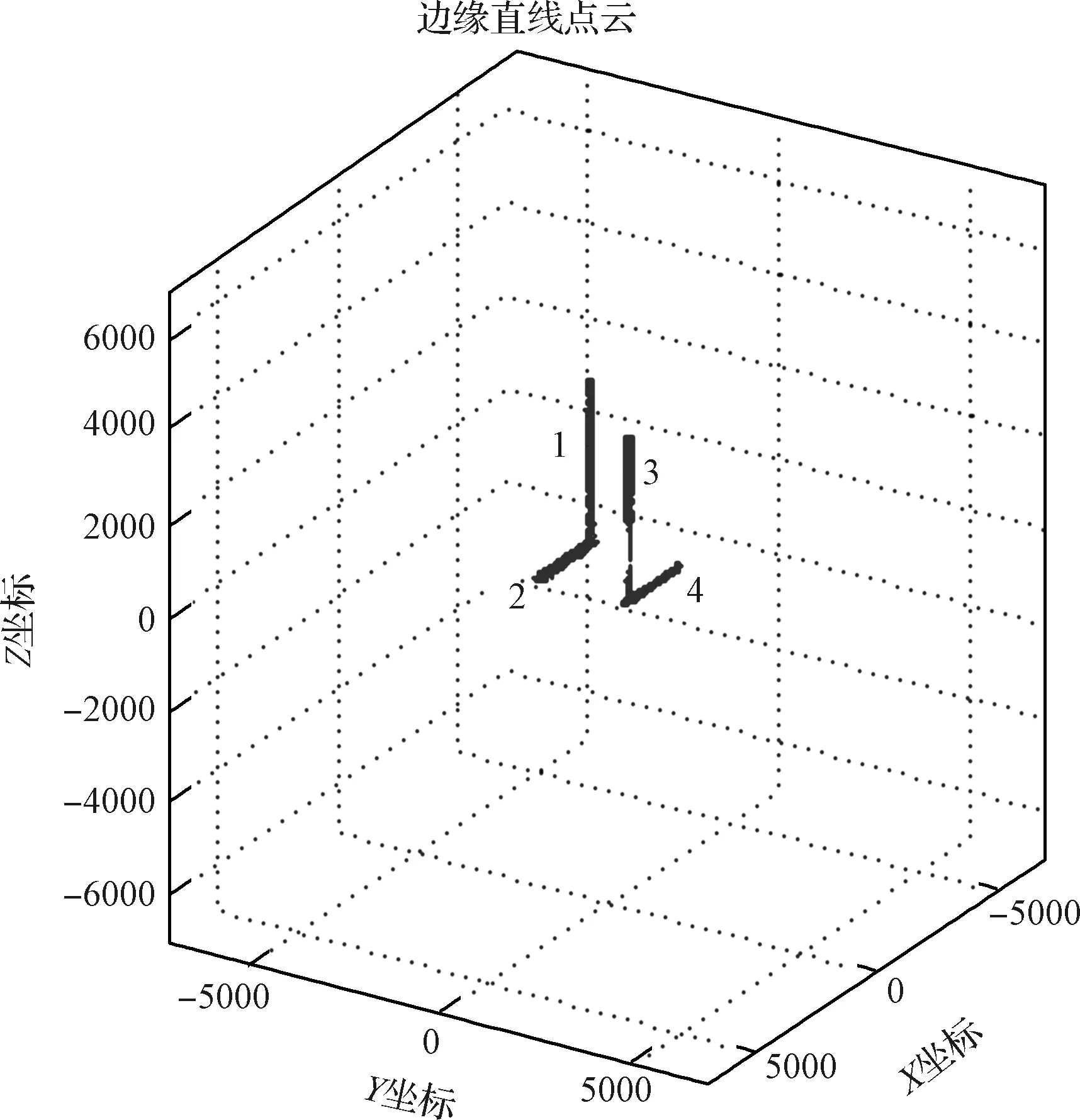
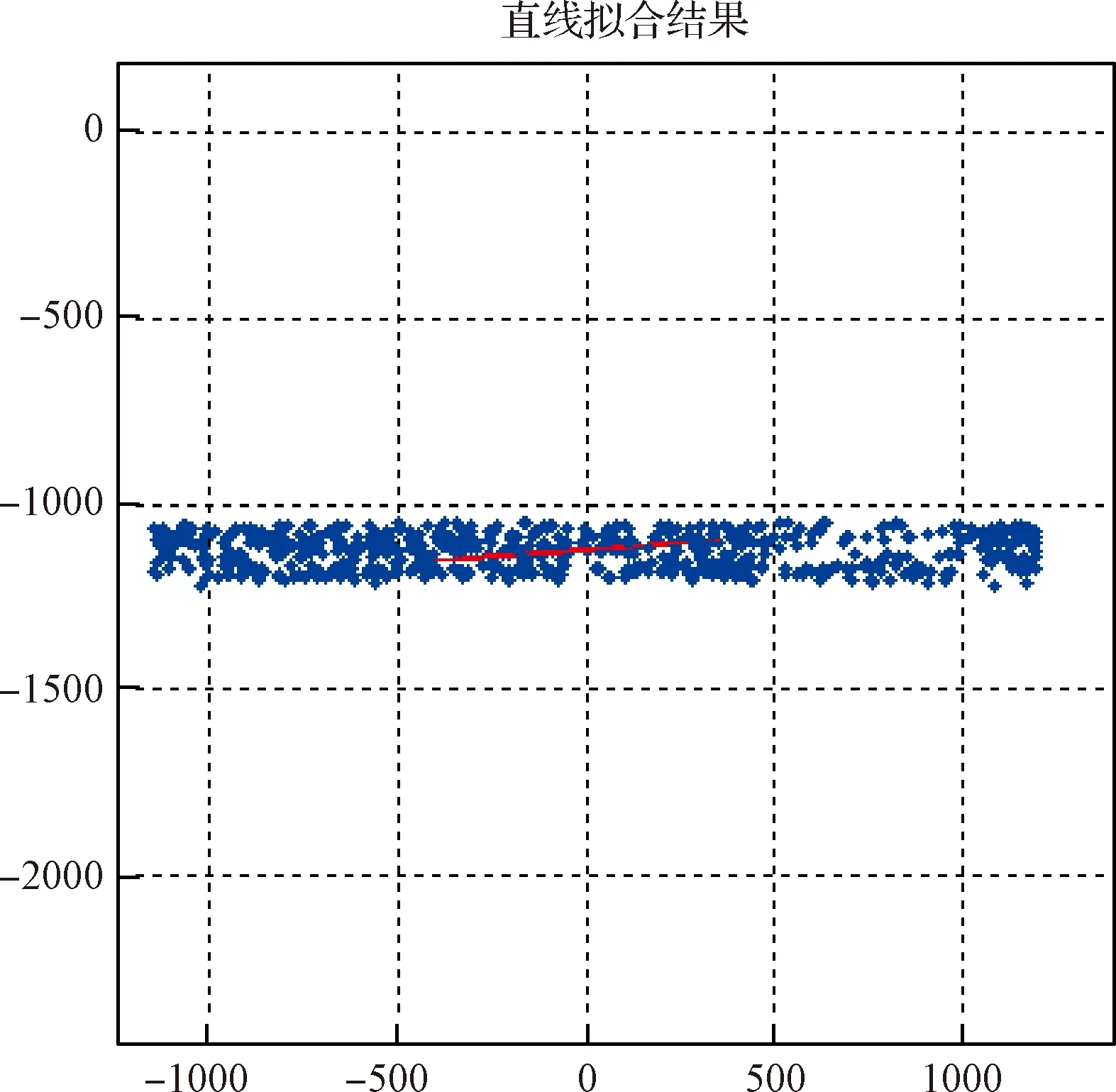
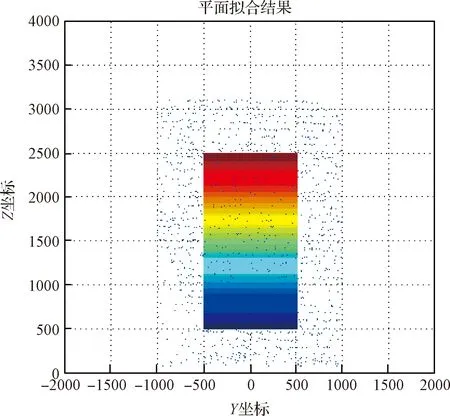
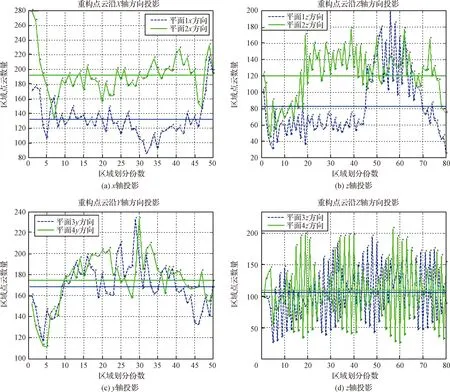
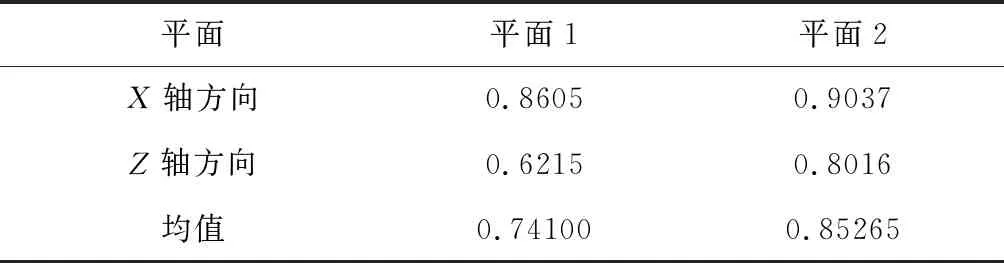
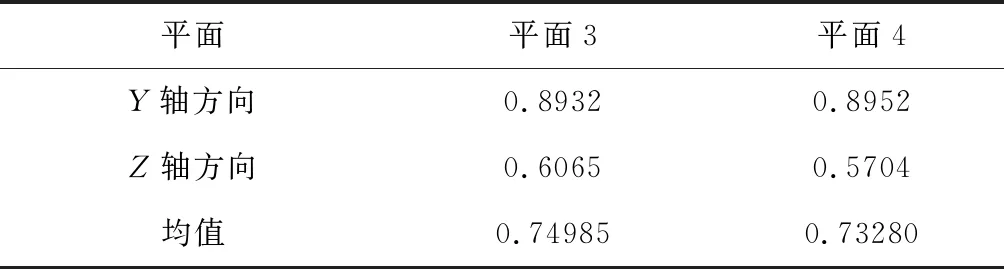
P(μ-3σ 意味著在(μ-3σ,μ+3σ]以外的概率不到0.3%,幾乎不可能發生,稱為小概率事件。因此,要精確得到平面方程就必須將上述獲得的平面方程采用3σ法則循環剔除誤差較大的點,直到沒有瑕疵點參與擬合平面為止,獲得最優空間平面擬合結果。 首先進行閾值設定,選取直線點云數據(Xj,Yj,Zj),j=1,2,3,…,N,再從中進行區域均勻采樣獲得部分采樣點(xj,yj,zj),j=1,2,3,…,n。依據采樣點進行空間直線擬合。 設空間直線方程為: (5) 整理獲得XOZ與YOZ平面的直線射影方程: (6) 式中: 因此,空間直線可以看作上述兩個平面相交的直線,如圖4所示,分別對2個方程進行數據擬合。設式(7)表示按擬合方程x=az+b求得的近似值。一般地,它不同于實測值xi,兩者之差由式(8)所示: (7) (8) 同理得: (9) 圖4 空間直線示意圖Fig.4 Schematic diagram of space line 當滿足下列方程時Q值最小,即可獲得方程的系數a,b,c,d的值。 (10) 令: (11) 則方程組可寫成: FFTA=FX,FFTB=FY 式中: 根據n組數據點解方程組獲得a,b,c,d的值,即求得直線方程。同理,采用上述3σ法則循環剔除誤差較大的點,直到沒有瑕疵點參與擬合直線為止,獲得最優空間直線擬合結果。 空間非合作目標三維形貌結果是否滿足精度要求至關重要。因此,本文建立三個評估指標以及多因素綜合評估對重建結果進行評價,驗證空間非合作目標重建精度及滿意度。 選取重建點云平面分布范圍為M×N,點云數量為Q,將其均勻劃分成m×n塊,用Kd表示含有點的分塊個數,用Kt表示總的分塊數,Md表示點云的密集程度。 (12) (13) 令Nc為分割小塊的點云總數量,Dij為塊內點云密度,如圖5所示。其中i,j為整體點云第i行j列的小分塊,設小分塊正方形的邊長為L,可由式(14)求得。因此小分塊正方形的面積Sc為: (14) (15) 且正方形的面積也可以由點云數據的X、Y坐標值范圍求得: Sc=(ymax-ymin)×(xmax-xmin) (16) 因此可得塊內點云密度的計算公式為: 圖5 分塊點云密度計算Fig.5 Block point cloud density calculation 其中:Md對整體點云密度也有影響。可能存在點云數量多,但Md較小,意味著有較多分塊不存在點云,導致局部密度很大,因此本文密度計算公式如下所示: (17) Dden受分塊閾值影響,因此,本文采用先確定閾值,再自動確定m與n值。同時密度的標準為D標準,實際應用中應考慮實際情況加以選用。 采用2.1中平面擬合結果,分析平面與平面之間的平行度與垂直度關系。由于測量存在誤差,導致獲得的目標示意圖如圖6所示: 圖6 目標示意圖Fig.6 Schematic diagram of the target 則面與面之間夾角為: (18) 采用2.2中直線擬合結果,分析直線與直線之間的平行度與垂直度關系。則直線與直線之間夾角為: (19) 通過下式計算出模型平面所有點云數據到擬合平面距離: di=ajXi+bjYi+cjZi+1,i=1,2,…,N,j=1,2,…,n (20) 將平面沿著Z方向投影,則殘差值的極大值為: max|zi-(-1-a0xi-a1yi)/a2|,i=0,1,2,…,n-1 (21) 當前觀測點到擬合平面的距離小于各觀測點與擬合平面殘差絕對值的極值,則當前觀測點在選擇的表面上重構,即為表面重構點。 (22) 假設將最優結果100%對應數學描述為5,即可通過計算反求得點云密度、幾何性質以及表面完整度對應的數字S密度,S幾何,S完整度。 S總=S密度×γ+S幾何×η+S完整度×μ (23) 其中:γ+η+μ=1 采用偏大型柯西分布和對數函數作為隸屬函數,如下式所示: (24) 其中:α,β,a,b為待定系數: 將滿意度劃分為5個等級,分別對應數學描述為5、4、3、2、1。 當對評估結果“很滿意”時,隸屬度設為100%,即f(5)=100%; 當對評估結果“較滿意”時,隸屬度設為80%,即f(3)=80%; 當對評估結果“很不滿意”時,隸屬度設為1%,即f(1)=1%。 將上述結果代入上式即可求得: 所以隸屬函數為: 將評估結果S總代入上式即可獲得多因素評估結果滿意度。 1)定義非合作目標坐標系、平臺雷達坐標系、世界坐標系,明確其之間的關系;建立可測點云提取機制,精確提取某一視場角數據;依據線陣激光雷達工作原理與掃描機制,采用MATLAB模擬空間環境,建立仿真系統,實現激光雷達環繞目標做360°繞飛跟蹤掃描,如圖7所示;再利用坐標系之間的轉換關系,獲得N幀可測點云數據,如圖8所示。 圖7 雷達采集數據示意圖Fig.7 Schematic diagram of radar acquisition data 圖8 可測點云數據Fig.8 Measurable point cloud data 2)將上述獲得的可測點云數據進行粗配準,再經過點云聚類分割后,采用最近迭代點(Iterative closest point,ICP)進行精配準,即可獲得旋轉與平移矩陣,其結果如圖9所示。 圖9 點云配準Fig.9 Point cloud registration 3)根據ICP點云配準方法得到的差分掃描點云數據之間的位姿增量關系,采用逆序三維重建方式,獲得重建點云模型[6],如圖10所示。 圖10 三維重建結果Fig.10 Three-dimensional reconstruction result 根據要求,分別提取主體點云數據的四個面,如圖11所示,進行評估實驗。 圖11 主體的四個平面點云Fig.11 Four plane point clouds of the main body 采用2.1中平面擬合方法,獲得4個面的法向量為: 采用2.2中直線擬合方法,獲得圖12中4條直線的方向向量,見表2。 1)點云密度 本文根據需求D標準=0.02 m,設分塊大小為200 mm×200 mm,將主體各平面點云劃分成10×15塊小正方形,各平面點云數量為6864、11233、8814、9021,通過計算獲得各面點云密度見表3: 表1 各平面法向量Table 1 Normal vector of each plane 圖12 直線點云Fig.12 Straight line point cloud 表2 各直線的方向向量Table 2 Direction vector of each line 表3 各平面點云密度Table 3 Point cloud density of each plane 2)幾何性質 根據擬合的直線公式,獲得圖13的直線擬合結果,再計算出直線之間的平行度與垂直度,見表4與表5。根據擬合的平面公式,獲得圖14的平面擬合結果。 圖13 直線擬合結果Fig.13 Straight line fitting result 表4 直線平行度Table 4 Straight line parallelism 表5 直線垂直度Table 5 Straight line perpendicularity 圖14 平面擬合結果Fig.14 Plane fitting result 計算出平面之間的平行度與垂直度,見表6與表7: 表6 平面平行度Table 6 Plane parallelism 3)表面完整度 進行重構點篩選后,將平面1與2中重構點數量沿著x軸方向投影與z軸方向投影,結果如圖15(a)與圖15(b)所示;將平面3與4中重構點數量沿 表7 平面垂直度Table 7 Plane perpendicularity 著y軸方向與z軸方向投影,結果如圖15(c)與圖15(d)所示。各平面的點云總數量如表8所示。再依據表面完整度計算公式,求得平面1與2的表面完整度如表9所示,平面3與4的表面完整度如表10所示。 圖15 重構點云數量投影折線圖Fig.15 Reconstructed point cloud number projection line chart 表8 各平面重構點數Table 8 Number of reconstruction points for each plane 4)多因素綜合評估結果 根據獲得的點云密度、幾何性質及表面完整度,求得對應的數字描述為: 表9 平面1與2表面完整度Table 9 Surface integrity of plane 1 and 2 表10 平面3與4表面完整度Table 10 Surface integrity of plane 3 and 4 S總=(S密度+S幾何+S完整度)/3=4.467275 將S總代入式(24)中得到滿意度為: f(x)=95.5889% 綜上所述,本研究針對空間非合作目標重建質量評估問題,利用3σ優化法則進行平面與直線擬合,從點云密度、幾何性質與表面完整度三個方面進行評估,再進行多因素綜合評估獲得滿意度。仿真結果表明,該重建模型點云密度達到標準的概率為97.41%,表明重建結果較好;該重建模型幾何性質達到標準的概率為93.72%,重建幾何性質較好;該重建模型表面完整度達到標準的概率為76.9075%,是由于點云分布的比較隨機,因此重建表面完整度較差一些;多因素綜合評估滿意度為95.5889%,表明整體重建結果較好,符合要求。該研究不僅能夠驗證基于線陣激光雷達測量空間非合作目標重建結果的準確性,且建立的多因素綜合評估方法還為未知構型評估提供一種新的研究方向。2.2 空間直線擬合
3 空間非合作目標重建質量評估
3.1 重建點云密度
3.2 重建幾何性質
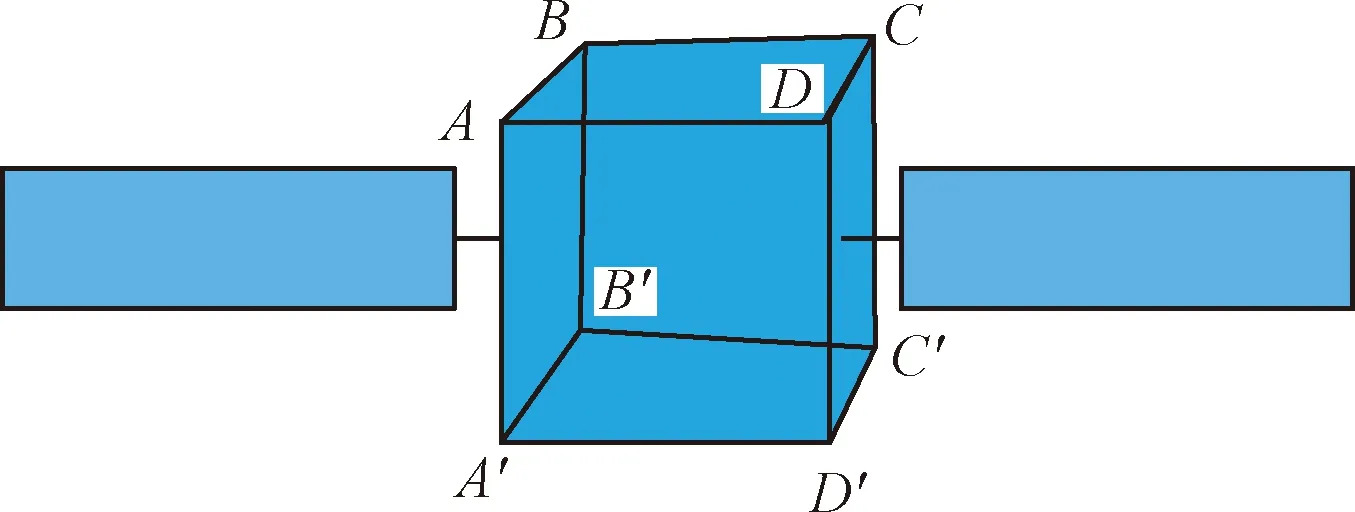
3.3 重建表面完整度
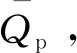
3.4 多因素綜合評估
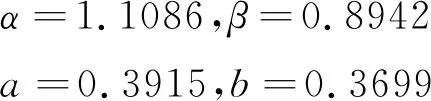
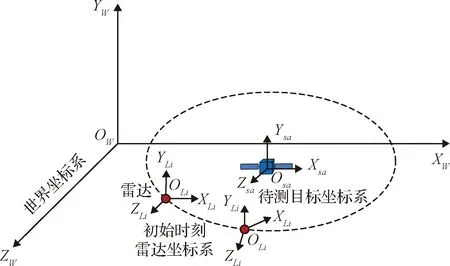
4 目標重建實驗評估結果
4.1 目標三維重建結果
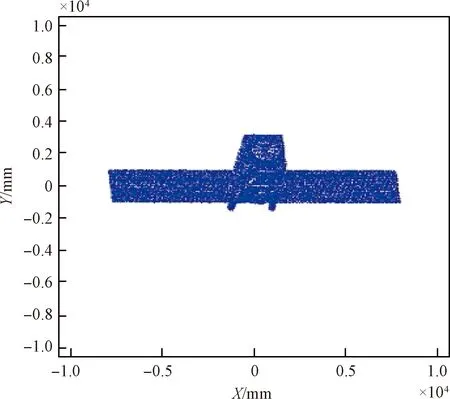


4.2 擬合結果
4.3 質量評估結果








5 結 論

