運載火箭姿態系統自適應神經網絡容錯控制
馬艷如,石曉榮,劉華華,梁小輝,王 青
(1. 北京航空航天大學自動化科學與電氣工程學院,北京 100191;2. 北京控制與電子技術研究所,北京 100038;3. 西北工業大學自動化學院,西安 710072)
0 引 言
運載火箭作為太空探索的重要工具,成為許多國家研究重點,例如美國NASA的Ares系列和中國長征系列運載火箭等[1-3]。運載火箭承擔載人飛船等任務,發射任務一旦失敗,不僅會帶來巨大的經濟損失,還會影響整個國家的軍事和外交等。運載火箭控制的主要挑戰是在出現干擾、動力學未建模或建模錯誤和執行器故障等情況時仍能保證高性能,因此穩健而可靠的飛行控制系統必不可少。
傳統飛行控制方法采用增益調度和比例積分微分控制器,而運載火箭氣動環境復雜,干擾和不確定性大,采用傳統飛行控制方法對其飛行過程進行高精度控制存在一定的難度。為解決上述問題,許多學者提出了先進控制理論[4],如滑模控制[5-8]、自適應神經網絡控制[9-13]和非參數自適應控制[14]等方法。文獻[15]針對具有外部干擾和模型不確定性的運載火箭設計了一種非奇異快速終端滑模面,并設計了相應的固定時間控制器。文獻[16]針對衛星運載火箭姿態控制系統設計了一種基于直接自適應動態反演控制律。文獻[17]針對存在外部干擾和參數不確定的運載火箭設計了一種復合自適應模糊H∞控制律。文獻[18]針對運載火箭上升段在復雜飛行環境、大不確定性干擾和振動等因素的影響下,傳統控制方法難以滿足高品質控制需求的問題,進行了自適應增廣控制方法研究,以實現對運載火箭姿態的精確控制。文獻[19]設計了一種自抗擾控制器抑制運載火箭自身結構參數變化和內外擾動對姿態控制精度和姿態穩定性的影響。
本文針對存在執行器故障的運載火箭姿態控制系統,設計了一種基于自適應徑向基神經網絡滑模非線性控制律。主要創新點如下:1)直接針對運載火箭非線性姿態動力學模型進行控制律設計,無需對模型進行線性化處理。2)在控制律設計中不僅考慮未知外部干擾,還考慮由于故障可能帶來的系統模型發生變化的影響。3)將應用于單輸入單輸出的自適應徑向基神經網絡滑模非線性控制律[20]擴展到多輸入多輸出系統。4)對本文所設計的控制律進行仿真驗證,姿態跟蹤誤差收斂至零,確保了算法的實用性。
1 系統動力學模型
對于某大型運載火箭,考慮安裝6臺發動機,其中,助推發動機4臺,作單向擺動;芯級發動機2臺,作雙向擺動,圖1為火箭發動機布局,箭頭方向為發動機擺動方向。火箭三通道姿態可以解耦控制,其中,俯仰通道的控制依靠助推和芯級發動機2、4號擺動實現;偏航通道的控制依靠助推和芯級發動機的1、3擺動實現;滾轉通道則需要所有發動機擺動共同參與。
考慮外部干擾,且忽略其彈性模態,建立運載火箭姿態控制系統模型[21]:
(1)
式中:Ω=[θ,α,β]T為姿態角向量,θ為滾轉角,α為偏航角,β為俯仰角;ω=[ωx,ωy,ωz]T為角速度向量;J為運載火箭轉動慣量矩陣;u為控制輸入向量;d為未知的外部干擾向量。S,ω×分別為:
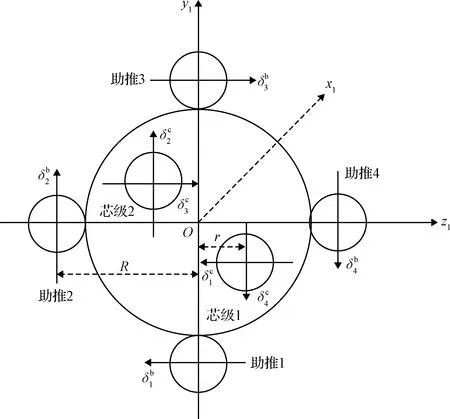
圖1 運載火箭發動機布局尾視圖Fig.1 Configuration of propulsive rocket engines (view from tail)
等效擺角與芯級發動機、助推發動機擺角關系為:
(2a)
(2b)
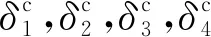
(3)
式中:P為發動機推力;XR為發動機噴嘴到火箭頂端的距離;XZ為質心位置;R和r為發動機中心到運載火箭x軸的距離。則控制力矩可以表示為:
u=Bδ
(4)
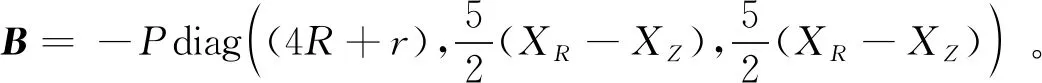
(5)
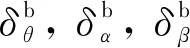
本文考慮助推發動機或者芯級發動機出現卡死或失效故障,其故障模型為:
(6)
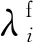
定義助推發動機和芯級發動機實際擺角為:
(7)
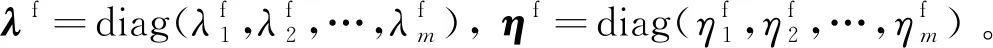
由式(1)-式(7),建立運載火箭動力學模型:
(8)
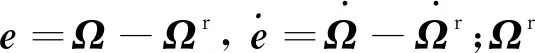
(9)
式中:f(x)∈R3,G(x)∈R3×3,D∈R3,且定義如下:
(10)
2 運載火箭姿態系統自適應徑向基神經網絡容錯控制
運載火箭姿態系統跟蹤控制器的目標是對存在模型不確定性、未建模動態和外部干擾等情況的姿態跟蹤系統設計控制器,使得姿態角跟蹤誤差e能夠在有限時間收斂至零。本文針對式(9)描述的運載火箭姿態跟蹤系統設計了一種終端滑模控制律;在終端滑模面基礎上,利用自適應參數的徑向基神經網絡逼近系統參數;設計自適應控制項,用來補償擾動和近似過程誤差,以增強系統閉環穩定性和改善瞬態性能。
2.1 終端滑模面設計
在進行控制器設計前,先給出3個假設。
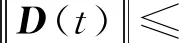
假設2.控制輸入向量δ(t)∈L2空間,即δ(t)在任何有限時間內的積分均有界[21]。
假設 3.姿態角指令信號Ωr連續,其前兩階導數一致連續且有界[21]。
為了確保跟蹤誤差e在有限時間內收斂至零,設計如下非奇異終端滑模面:
s=x2+C1x1+C2sigl(x1)
(11)
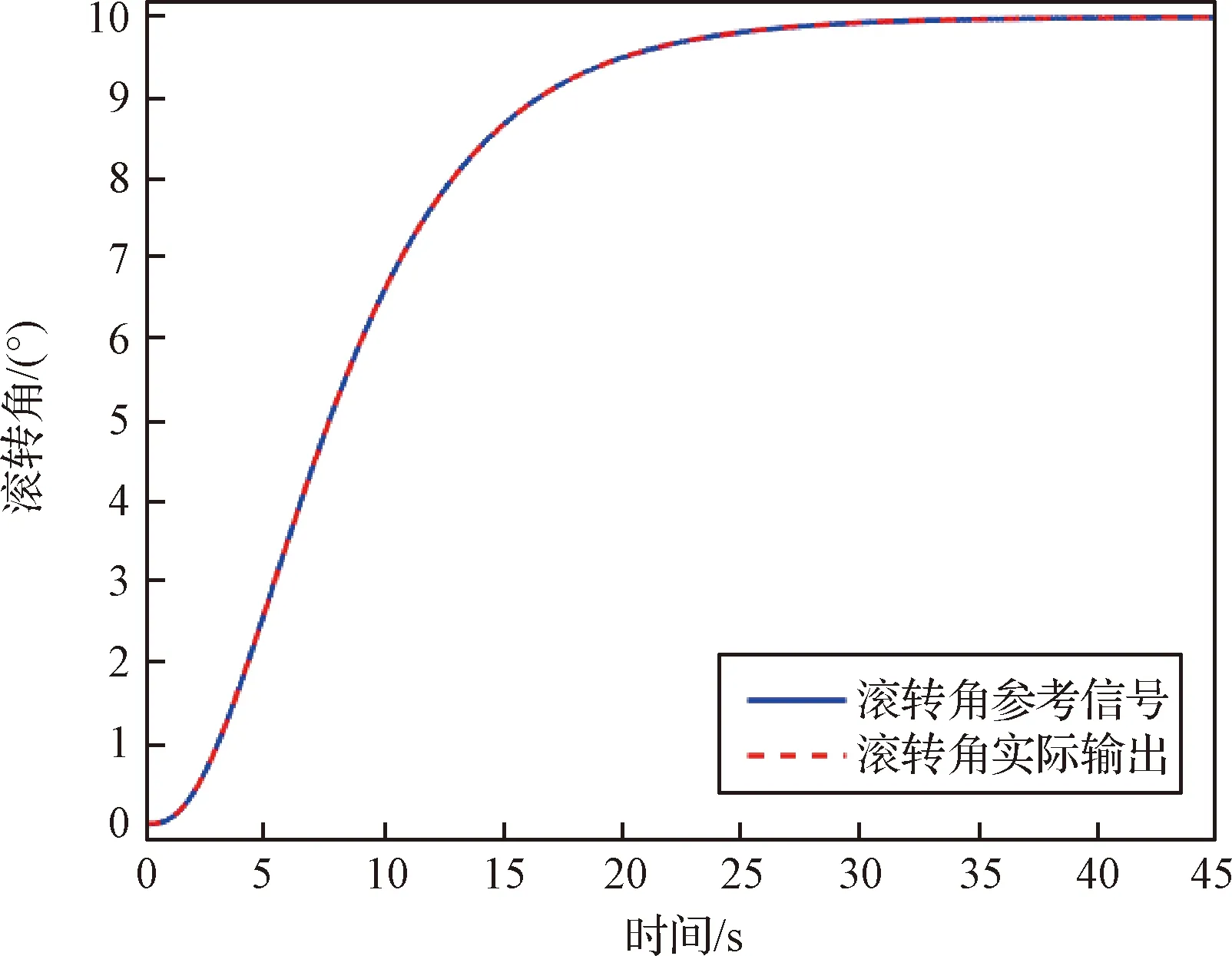
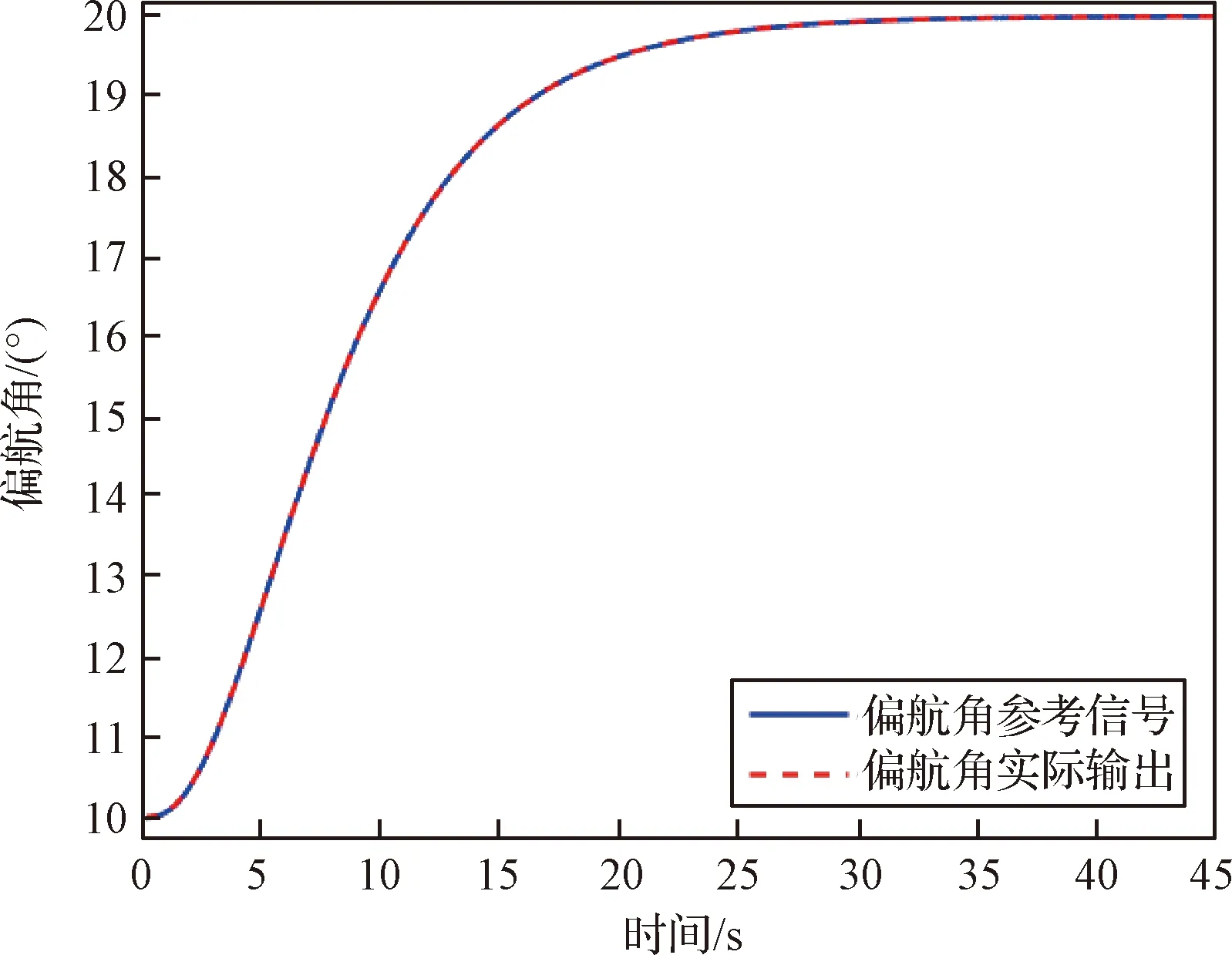
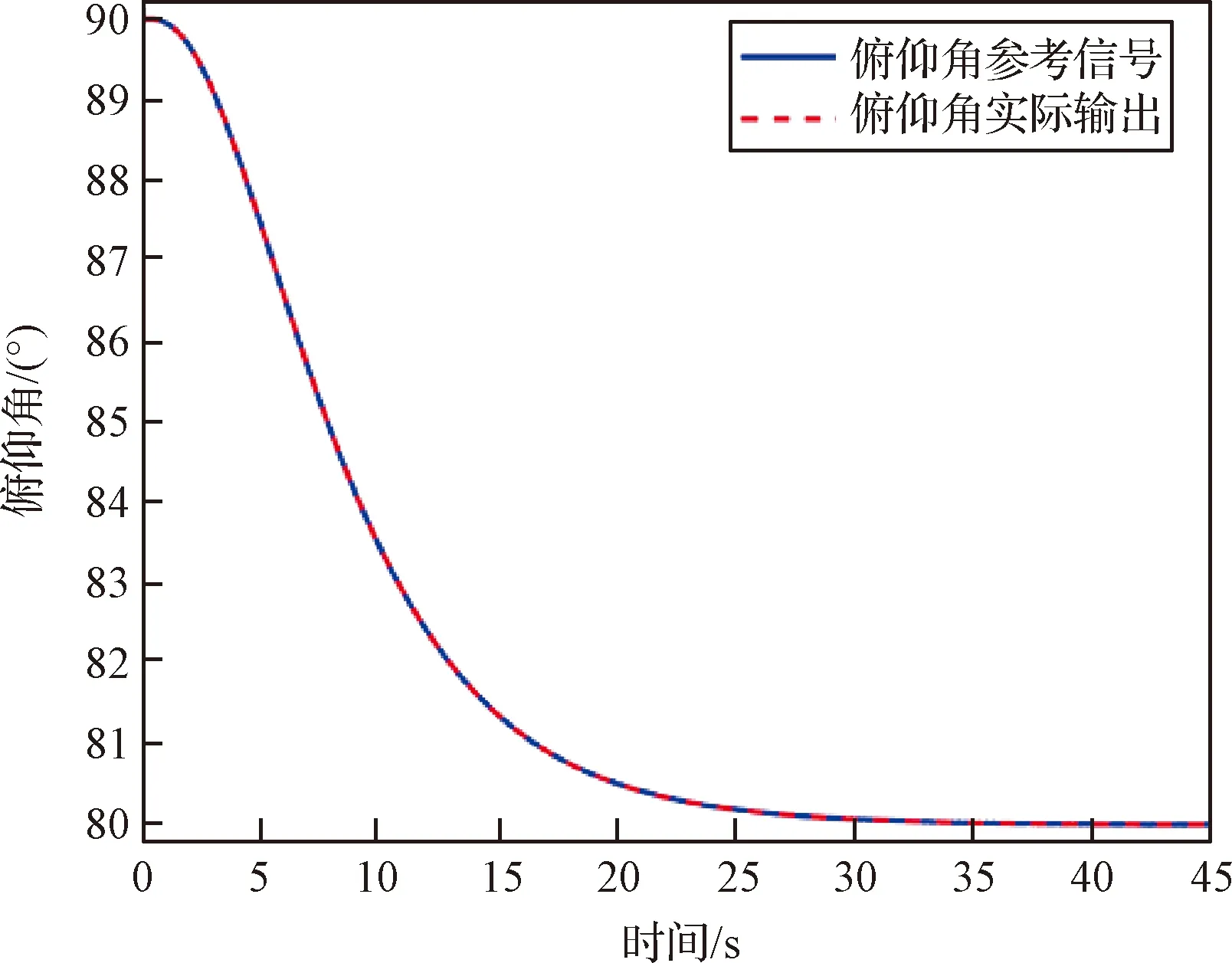
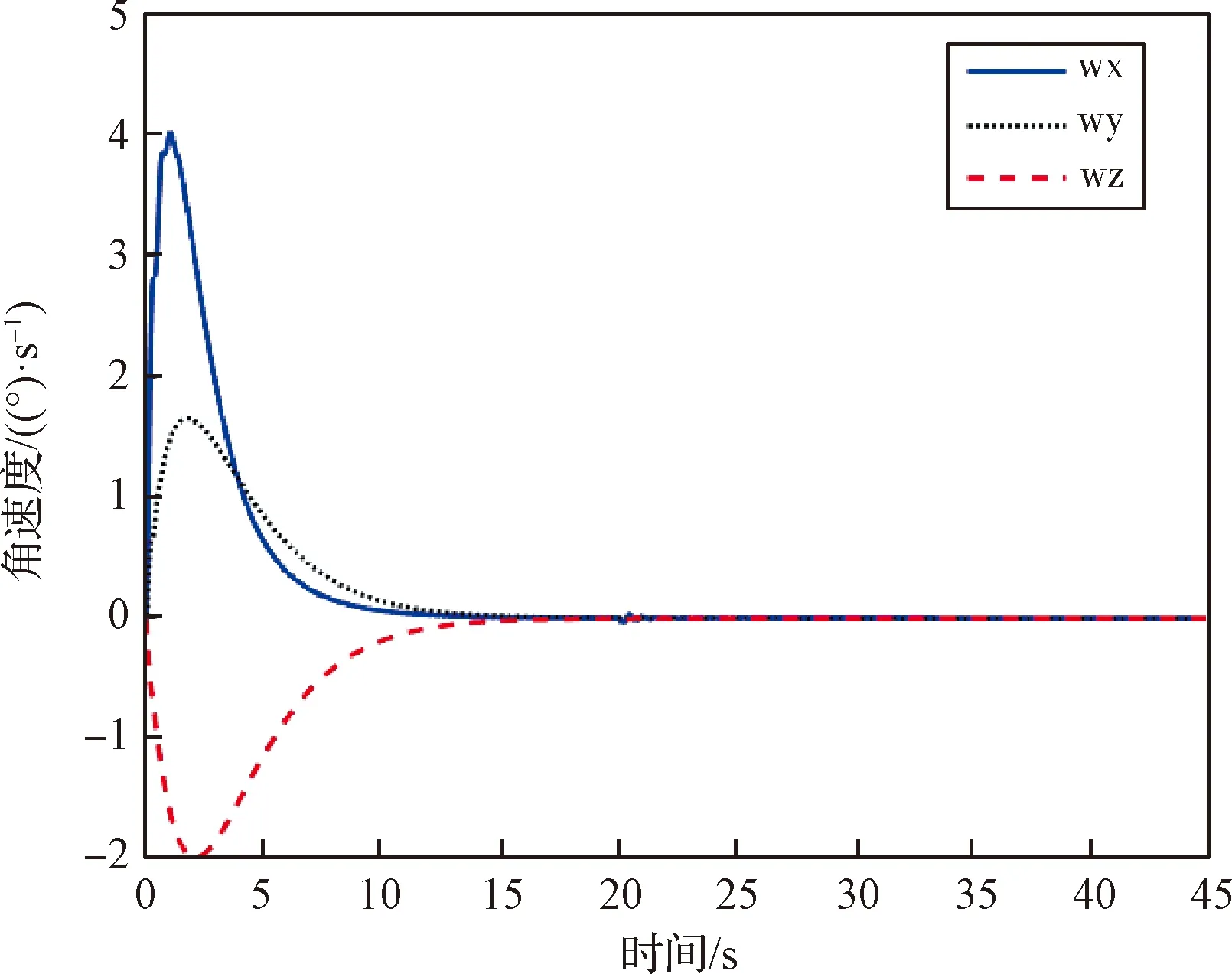
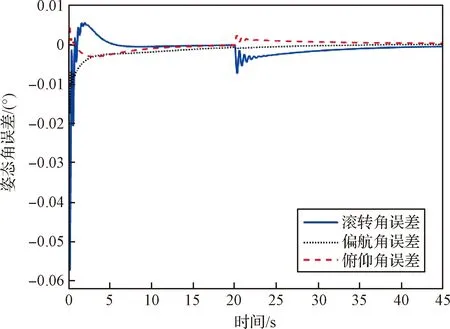
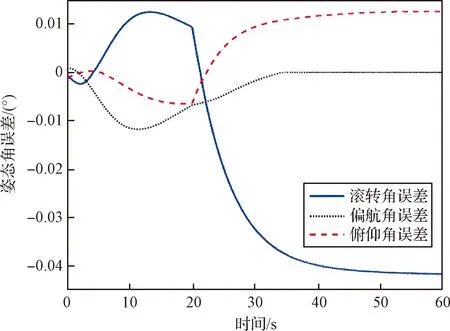
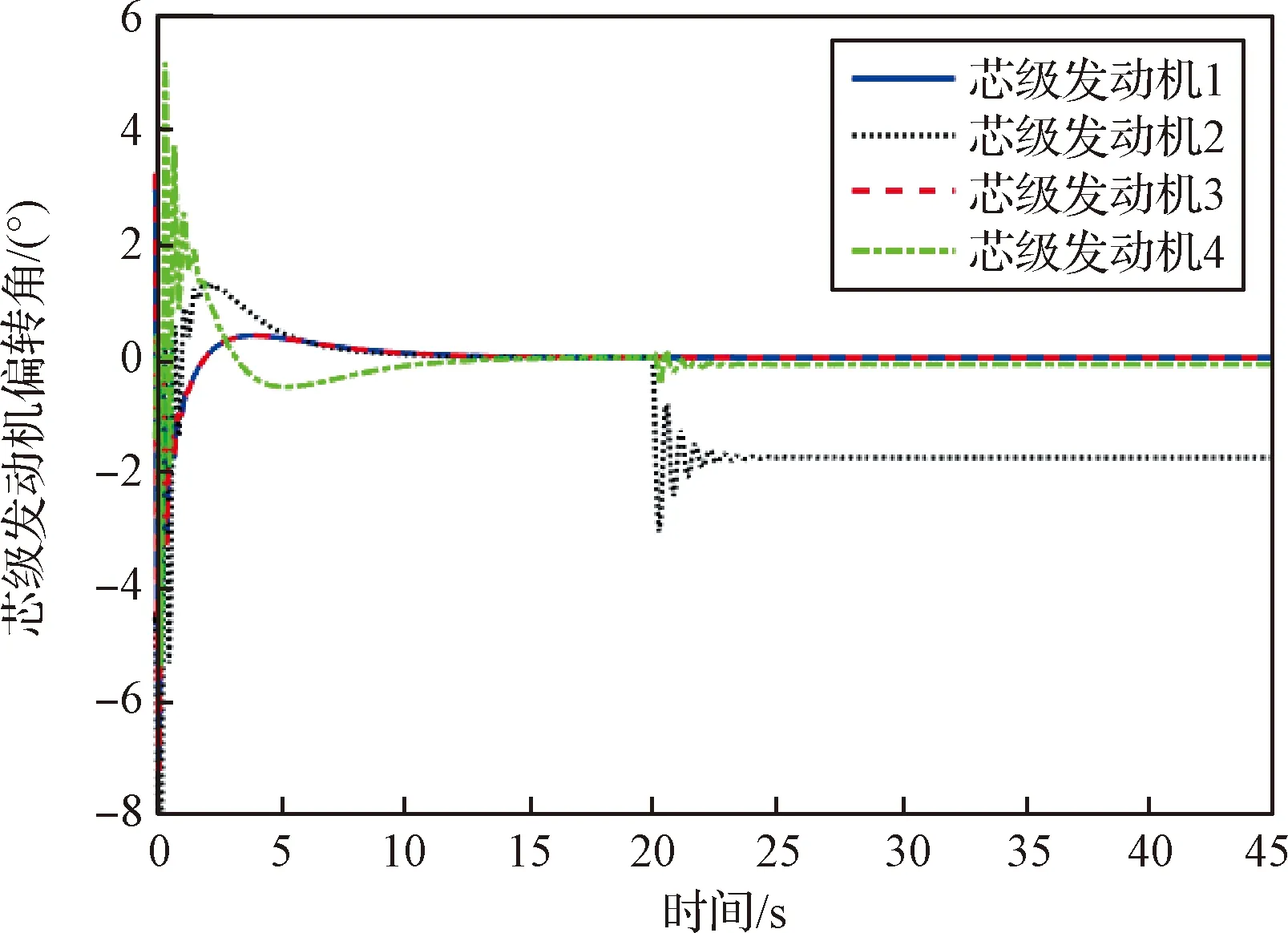
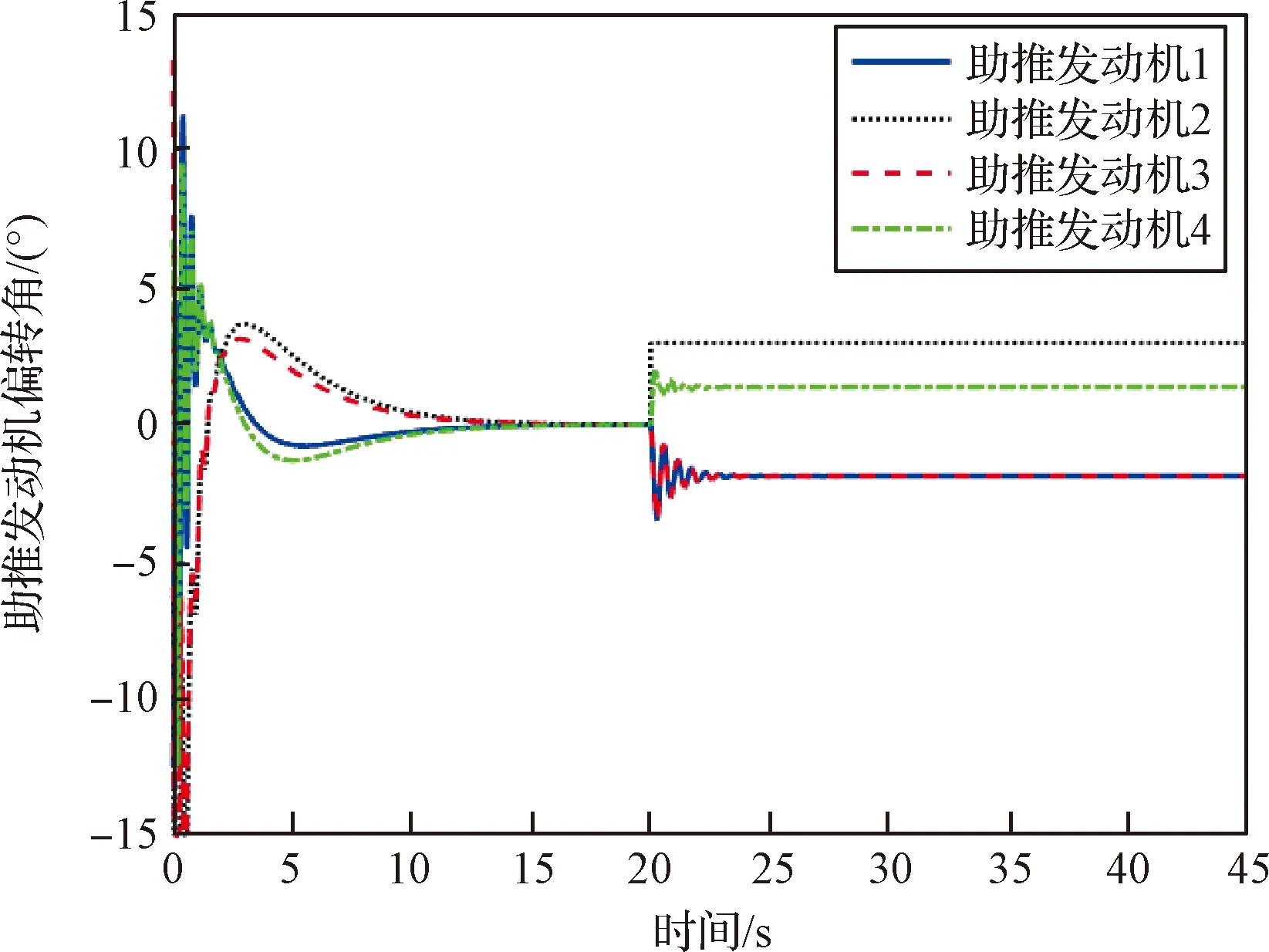
式中:s=[s1,s2,s3]T∈R3, 0 (12) 針對滿足上述假設條件下的運載火箭姿控系統,提出了本文的定理1。 定理 1.對于式(9)所示的運載火箭姿態跟蹤系統,在假設1-3成立的前提下,若采用式(11)所設計的滑模面,且控制器設計如下: δ=δeq+δd (13) (14) 證明:定義Lyapunov候選函數為: (15) (16) 將式(13)和式(14)代入式(16)可得: (17) (18) 當運載火箭在運行過程中,某個執行機構發生故障,即整個過程中系統模型會發生較大的變化,采用上述終端滑模控制律控制精度可能較差。本節利用徑向基神經網絡逼近系統參數,當系統參數發生變化時,通過徑向基神經網絡進行逼近,增加自適應控制項,用來補償擾動和近似過程中誤差,增強系統閉環穩定性和改善瞬態性能。 由徑向基神經網絡的逼近特性可知,非線性函數h(x)可以表示為: h(x)=(W0)TΦ0(x)+ε0=h0(x,c,σ)+ε0(19) (20) F(x)=(W0)TΦ0(x)+ε0=F0(x,c,σ)+ε0 (21) 將式(19)代入式(16),可得: (22) 式(22)可寫為: (23) (25) 由式(23)、(24)和(25)可得: (26) 用ζ代替外部干擾、參數不確定、估計誤差和線性化誤差: ζ=D+ε1+ε0 (27) 式(26)可寫為: (28) 定理 2.對于式(9)所示的運載火箭姿態跟蹤系統,在假設1-3成立的前提下,式(29)所設計的控制律使得運載火箭姿態跟蹤系統誤差在有限時間內收斂至零。 u=G-1(x)(utsm+uRBFNN+uad) (29) 式中:utsm為終端滑模控制項;uRBFNN為使用徑向基神經網絡逼近的非線性函數F(x);uad為自適應控制項,用來補償擾動和近似過程誤差,增強系統閉環穩定性和改善瞬態性能。三個控制項定義為: (30) (31) 證明:定義Lyapunov候選函數: (32) (33) 將式(28)代入式(33)中,可得: (34) (35) 將式(31)代入式(35)中,可得: (36) 并將式(31)代入,則有: (37) 仿真中,考慮系統如下兩種可能的模式: 正常模式:所有執行器正常運行,即λf=diag(1,1,…,1),ηf=0。 表1 運載火箭仿真中的參數Table 1 Parameter of launch vehicle used in numerical simulations 仿真考慮如下情況,系統在前20 s正常運行,當t=20 s時,助推發動機2發生卡死故障,且卡死偏移為σ=3°。所設計的控制律姿態角跟蹤結果如圖2-4所示。圖2-4分別為滾轉角、偏航角和俯仰角跟蹤軌跡。由圖2-4可知,通過所設計的自適應徑向基神經網絡控制律,運載火箭姿態控制系統能夠跟蹤姿態指令信號。圖5為角速度變化曲線,圖6為采用自適應徑向基神經網絡控制的姿態 圖2 滾轉角跟蹤軌跡Fig.2 Tracking trajectory of roll angle 圖3 偏航角跟蹤軌跡Fig.3 Tracking trajectory of yaw angle 圖4 俯仰角跟蹤軌跡Fig.4 Tracking trajectory of pitch angle 圖5 角速度變化曲線Fig.5 The curve of angular rate angular velocity 角跟蹤誤差信號,圖7為系統采用非奇異終端滑模控制律得到的姿態角跟蹤誤差信號。對比圖6和圖7可知,采用自適應徑向基神經網絡控制律的誤差收斂速度比終端滑模控制律的誤差收斂速度快,當故障發生時,其誤差信號也能快速收斂為零。而 圖6 姿態角跟蹤誤差,本文方法Fig.6 Tracking error of attitude angle 終端滑模控制律最終收斂到接近于零的常數。圖8為運載火箭芯級發動機擺角變化曲線,如圖8所示,當助推發動機2在20 s發生卡死故障時,芯級發動機1、3和4擺角不變,芯級發動機2擺角發生變化,且在較短時間內收斂至一個常數。圖9為運載火箭助推發動機擺角變化曲線,如圖9所示,助推發動機 圖7 姿態角跟蹤誤差,終端滑模方法Fig.7 Tracking error of attitude angle 圖8 芯級發動機偏轉角曲線Fig.8 The curve of central rocket engines deflection angle 圖9 助推發動機偏轉角曲線Fig.9 The curve of strap-on rocket boosters engines deflection angle 2在20 s時發生突變,且維持在某個常數不變;助推發動機1、3和4也發生變化,且在較短時間內收斂至某個常數。即當運載火箭某個助推發動機發生故障時,控制器通過控制其余助推發動機和芯級發動機擺角來平衡該故障帶來的影響。因此,本文所用方法在運載火箭執行器卡死故障下仍具有較高的控制精度和魯棒性。 本文針對存在執行機構卡死故障的運載火箭姿態跟蹤系統設計了一種基于終端滑模自適應徑向基神經網絡控制律,所設計的控制器能夠確保系統在較短時間內收斂至零,連續變化的控制律完全消除了滑模控制中的抖振現象。此外,該控制器僅用到控制輸入矩陣的信息,利用徑向基神經網絡逼近系統參數,采用自適應控制項補償外部干擾和近似過程中的誤差,使其具有較好的魯棒性,仿真結果表明基于終端滑模自適應徑向基神經網絡控制律具有較好的控制效果。
2.2 自適應徑向基神經網絡控制
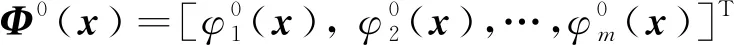
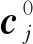
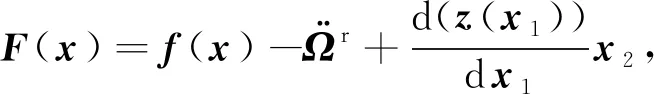
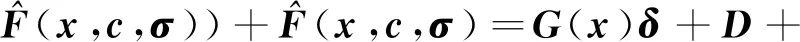
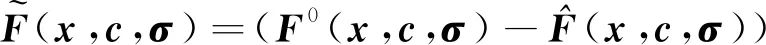
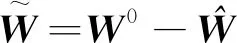

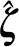
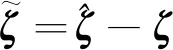
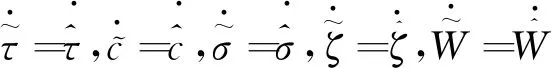
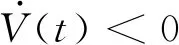
3 仿真校驗


4 結 論

