結合半參數方法和貝葉斯抽樣技術的多響應優化設計

汪建均, 郜婷玉, 楊世娟

(南京理工大學經濟管理學院,江蘇南京 210094)

1 引 言

響應面方法(response surface methodology,RSM)通常被認為是利用試驗設計、響應模型和優化方法獲取最優工藝參數的一種統計分析方法[1].統計學家Myers 等[2]曾明確指出“從更廣泛的意義上看,響應曲面方法已經成為整個工業試驗的核心”.隨著顧客需求層次的多樣化以及產品性能的穩步提升,在實際的產品與工藝過程中,往往需要考慮多個質量特性,因此多響應曲面優化設計問題在持續性質量改進活動中顯示出越來越重要的作用[3?5].

多響應曲面優化設計通常包括試驗設計、模型構建以及參數優化三個階段,其中響應曲面模型構建至關重要[6].在多響應曲面優化設計中,研究者首先需要構建合適的度量指標.然而,由于涉及到多個質量特性,因此在度量指標構建中往往需要考慮多響應之間的相關性、模型參數的不確定性、預測響應的波動以及過程的穩健性[7].在多響應曲面的優化設計中,常見的優化策略是通過數據降維方法將多響應的優化問題轉換為單一指標的優化問題,其中具有代表性的方法為:滿意度函數方法、多元質量損失函數和后驗概率方法等.比較而言,滿意度函數方法簡單實用,并且能夠在一些常用統計軟件如MINITAB 中加以使用,因此引起一些研究者和質量工程師的廣泛關注.例如,He 等[8]綜合考慮穩健性和最優性提出了一個新的滿意度函數模型,有效地解決了傳統滿意度函數未考慮多響應優化過程的穩健性問題.然而,滿意度函數方法難以有效地考慮多響應之間的相關性、預測響應的波動以及模型參數的不確定性.為此,一些研究者運用質量損失函數來實現多響應優化設計.例如,Ko[9]擴展傳統多元質量損失函數,進一步地考慮多響應的預測性能和穩健性能,有效地兼顧過程的偏差、穩健性以及預測性能之間的平衡.然而,正如文獻[9]中所指出的那樣“所提出的多元質量損失函數未能考慮模型參數不確定性對優化結果的影響”.

在響應曲面建模過程中,研究者期望通過響應曲面模型來反映試驗因子與多響應之間精確的函數關系,從而獲得更為合理的參數優化結果.但是,正如著名統計學家Box[10]所言“所有的模型都是錯誤的,但是有些模型是有用的”.傳統的響應曲面建模方法通常事先假定響應曲面模型結構,然后采用參數方法加以估計.然而,在很多情況下,所假設的響應曲面模型結構并不符合客觀的實際情況,從而導致無法獲得可靠的研究結果,甚至出現錯誤的研究結論.因此,在響應曲面模型構建過程中需要考慮模型不確定性(模型參數以及模型結構不確定)對優化結果的影響.為此,Peterson[11]在標準的多響應曲面(standard multi-response models,SMR)框架下利用貝葉斯方法考慮了模型參數不確定性對優化結果的影響,進而利用蒙特卡洛方法分析了優化結果的可靠性,即未來響應預測值落在產品規格限內的概率.Peterson 等[12]指出SMR 模型通常假設各個響應的模型結構是相同的,即模型所包含的因子效應是完全相同的.然而,在很多情形下響應模型所包含的因子效應往往是完全不同的.鑒于此,Peterson 等[12]在似不相關回歸模型(seemingly unrelated regression,SUR)的框架下利用貝葉斯方法開展了多響應優化設計.針對多響應優化問題,汪建均等[13]在貝葉斯統計建模框架下利用SMR和SUR模型結合多元質量損失函數和后驗概率方法,全面地考慮多響應之間的相關性、多元過程的穩健性、多目標之間的沖突以及優化結果的可靠性.上述響應曲面建模方法均事先對模型結構和響應分布等做出一些假設.然而,Min 等[14]指出“傳統的參數回歸方法通常需要在擬合響應曲面模型之前假設響應與因子之間的模型結構,這往往與實際情況并不相符,從而導致出現不可靠的研究結果,甚至是錯誤的研究結論”.比較而言,非參數方法不需要事先假定模型結構,而是利用試驗數據本身所包含的信息自適應地擬合響應曲面模型,往往更加符合實際情況.因此,在多響應優化設計中,一些研究者嘗試地利用非參數方法開展響應建模工作,并取得一系列的研究成果.Vining 等[15]認為參數模型不能較好的刻畫方差模型與各因子間的關系.因此他們采用基于核估計的非參數方法構建均值模型與方差模型,并指出非參數方法所構建的響應曲面模型的預測性能要優于基于二階多項式模型所構建的響應曲面模型.Ouyang 等[16]結合Bootstrap 方法和Pareto 優化提出一種集成的徑向基函數(radial basis function,RBF)神經網絡方法,并利用該非參數方法進行了參數優化設計.另外,一些研究者也考慮利用非參數方法對非正態響應的質量設計問題進行了研究.例如,Fox 等[17]利用非參數方法對非正態響應的試驗設計進行了分析.針對具有重尾分布的非正態響應數據,Lim 等[18]結合平滑樣條方法提出了一種基于非參數分位數回歸的置信區間新方法,有效地解決上述非正態響應的質量設計問題.

雖然非參數方法不需要對模型結構進行事先的假設,從而在建模方面具有良好的靈活性,能夠直接根據觀測數據擬合響應的均值和方差模型.但是非參數方法往往依賴于相對大的樣本或空間填充設計, 樣本量偏小會可能導致響應波動較大.針對非參數方法的不足之處,一些研究者提出了一些能夠處理小樣本試驗數據的半參數方法.因此, 基于半參數的多響應優化設計方法也引起一些研究者的廣泛關注和興趣.Wan[19]認為非參數方法對稀松數據進行響應曲面建模時,通常會導致其響應方差過大,并指出半參數方法則能較好地處理該問題.Pickle[20]通過比較三種方法(即參數方法、非參數方法和半參數方法)的均值模型和方差模型的均方誤差值,驗證了所提半參數方法的有效性.他們提出了兩種半參數的建模策略,一種是模型穩健回歸方法1(model robust regression 1,MRR1);另一種是模型穩健回歸方法2(model robust regression 2,MRR2).在MRR1 中的組合成分中,一部分是響應的參數擬合項,另一部分是響應的非參數擬合項.該方法將這兩項的權重和設為1,只要假設其中某一項為未知的混合參數即可.在MRR2 的組合成分中,一部分為響應的參數擬合項,另一部分則替換為非參數殘差擬合.因此MRR2 默認參數項的權重為1,非參數項為小于1 的權重系數(即混合參數).其中,混合參數的選擇是基于數據驅動的漸近最優值表達式.Mays 等[21,22]通過仿真方法來選擇非參數模型的帶寬和混合參數,從而獲得更為穩健的半參數估計結果.此外,在該文獻中,他們還給出了一種新的懲罰準則作為選擇策略,并闡述了單獨使用參數或者非參數方法的局限性.Mays等[23]對混合參數進行漸近最優估計和模型可靠性估計,并通過一個小型仿真實驗驗證了所提方法的有效性.Wan 等[24]提出了以期望函數為優化目標函數的多響應穩健回歸方法,他們結合試驗數據和仿真數據對參數方法和半參數方法進行了對比研究.研究結果表明: 與參數方法相比,基于半參數優化方法的偏差和方差都更低.

目前,基于半參數方法的多響應優化設計仍然存在一些問題沒有得到很好地解決.例如,在多響應優化設計中,一些研究者往往沒有考慮模型不確定性以及隨機誤差所引起的預測響應波動,從而導致獲得不可靠甚至錯誤的研究結論.另外,由于多響應目標之間的沖突以及模型結構等不確定因素影響,其優化結果的可靠性(預測響應值落在所給定的規格限內的概率)也有待進一步研究.針對上述問題,本文結合半參數方法和貝葉斯抽樣技術提出一種新的多響應優化方法.首先,通過半參數方法建立可控因子與響應之間的多響應面模型;其次,利用質量損失函數建立期望目標函數,同時通過貝葉斯抽樣方法構建隨機誤差修正模型;然后,通過混合遺傳算法對所構建的模型進行參數優化,獲得最佳的參數設計值.最后,結合貝葉斯抽樣技術對所獲得參數優化結果進行穩健性評估,以考察其優化結果的可靠性.

2 非參數和半參數建模方法

當模型結構錯誤設定時,傳統的參數回歸方法可能會造成試驗數據擬合不合理.尤其是當研究問題比較復雜、模型不確定性較高時,這種模型擬合不恰當問題就更加突出.因此Anderson-Cook 等[25]提出了采用局部回歸思想的非參數方法對試驗設計進行擬合,以應對較為復雜的穩健參數設計問題.在通常情況下,在無法確定輸入因子與輸出響應之間的函數關系時,分析人員可以采用數據驅動方法來局部回歸擬合響應曲面模型.由于數據驅動方法不僅可以擬合線性模型也可以擬合高度復雜的非線性模型,因此基于數據驅動的非參數或半參數方法可以較好地構建穩健的響應曲面模型,從而能夠處理高度復雜的響應曲面優化設計問題.

2.1 非參數響應曲面建模

非參數方法是基于數據驅動的響應曲面建模方法,其回歸函數的形式和隨機誤差分布都不作嚴格要求.針對某一點的估計值,那些接近該點的響應通常假設比那些遠離該點的響應包含更多的信息.因此,為了得到一個光滑的函數,一些非參數方法會使用局部加權平均原理.局部平均的基本思想等同于尋找局部加權最小二乘估計量的過程.若無法確定響應曲面模型的具體形式,分析人員通常會考慮利用非參數方法進行響應面建模.非參數無需事先設定模型函數的基本形式,因此更加符合實際情況.常見的非參數方法有核函數回歸、局部多項式回歸和樣條回歸等方法.其中,局部多項式回歸本質上是核函數回歸的一種拓展.

非參數方法通常使用局部線性回歸(local linear regression,LLR),其中LLR 是1 階多項式回歸.非參數估計關鍵在于如何確定核函數.核函數的形狀和值域可以反映響應估計值f(x0)在估計點x0處所用到數據量的權重.由于核函數方法不利用有關數據分布的先驗知識,對數據分布也不附加任何假定,是一種從數據本身出發研究數據分布特征的方法.

針對需要預測的點x0=(x01,x02,...,x0k),核函數可以定義為

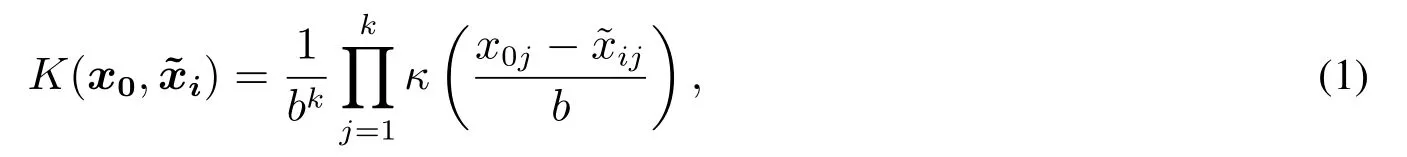
當對均值或者方差模型都使用非參數方法時,由于影響這兩種不同模型的控制因子可能不同,一般對均值模型使用二階模型,對方差模型使用一階模型,所以將使用不同的核函數.常見的核函數為高斯函數、均勻函數和三角函數等.根據Simonoff[26]的研究,核函數的變化并不會對估計值有很大的影響,所以本文將使用以往文獻中最為流行的高斯核函數,其形式為κ(u) = e?u2.K(x0,)中估計函數的平滑性取決于帶寬參數b.Mays 等[21]提出了新的懲罰預測誤差平方和技術(penalized prediction error sum of squares,PRESS??)進行合適的帶寬選擇,通過最小化PRESS??的函數值來尋求帶寬b的最優值.這里

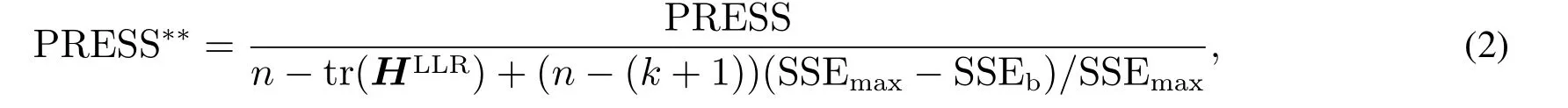
其中SSEmax代表所有可能帶寬值下的最大誤差平方和;SSEb是指特定某個帶寬值下的誤差平方和;k是回歸因子的個數, 一般是控制變量的個數; 分子部分是預測誤差平方和(prediction error sum of squares,PRESS).

留一法是指交叉驗證方法的一種, 假設樣本數據集中有N個樣本.將每個樣本單獨作為測試集, 其余(N ?1)個樣本作為訓練集,這樣得到了N個分類器或模型,用這N個分類器或模型的分類準確率的平均數作為此分類器的性能指標.每一個分類器或模型都是用幾乎所有的樣本來訓練模型,最接近樣本,這樣評估得出的結果與訓練整個測試集的期望值最為接近;HLLR是非參數方法LLR 得到的平滑矩陣

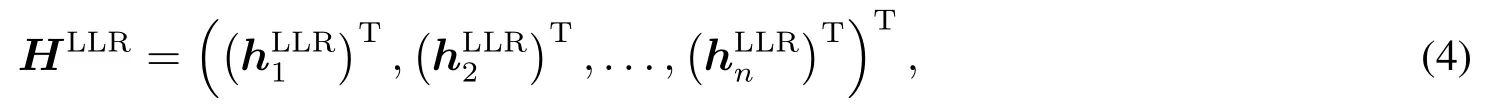
非參數方法具有良好的靈活性,能夠直接根據觀測數據擬合均值響應模型,但是這些擬合模型往往具有較高的方差.非參數方法往往依賴于相對大的樣本或空間填充設計.與非參數方法不同的是,半參數方法并不要求大量的樣本.在此,將重點介紹兩種常見的半參數方法.

2.2 半參數響應曲面建模

半參數方法顧名思義,就是結合傳統的參數方法和基于數據驅動的非參數方法的一個組合模型方法.針對以往的傳統參數方法無法處理: 第一,對基礎模型只有部分了解;第二,數據本身波動較高.這種情況下,用參數方法進行模型估計其誤差會較大.雖然非參數方法可以較好地處理上述問題,但是非參數方法對試驗數據的樣本量有較高的要求.半參數方法則可以充分發揮二者的優勢,較好地解決模型結構不確定和試驗數據樣本量小的問題.參數方法通常使用經典的最小二乘法OLS 進行參數估計,非參數方法則采用局部線性回歸LLR 進行估計,因此通過將傳統的參數估計和基于數據驅動的非參數方法進行有機整合就可以構成半參數方法.在此,將介紹兩種經典的半參數方法.

2.2.1 MRR1 方法

Robinson 等[27]提出了一種考慮均值響應建模的半參數方法,即通過一個混合參數λ結合參數和非參數部分.則可構建混合模型

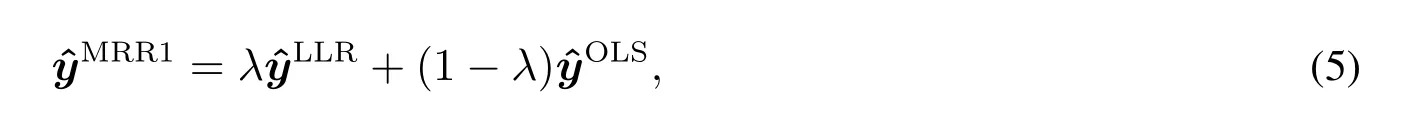
其中第一部分是通過非參數回歸得到的擬合向量和混合參數λ的乘積,第二部分是參數回歸得到的擬合向量和剩余比例部分的乘積.MRR1 通過給參數部分和非參數部分分配比例系數得到半參數模型,但是這種組合模型的波動在以往文獻中被證實較高,其中λ ∈[0,1]而這個λ的選擇法,類似于非參數部分的帶寬b的選擇,本質上是一種偏度方差的平衡,混合參數λ的漸近最優值用下面的數據驅動表達式來求得,即

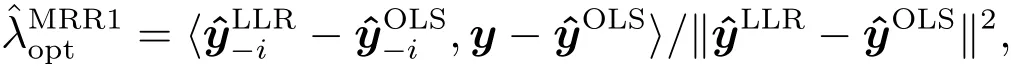
該半參數方法可以通過平滑估計獲取數據中的異常信息.此外,MRR1 方法不僅可以彌補參數方法整體擬合偏差大的問題,而且能夠處理非參數方法過度擬合的局限性,從而帶來響應面設計的穩健性.如果參數部分估計和非參數部分估計同時較高或者較低,MRR1 估計也會過高或者過低.因此,有必要引入MRR2 半參數方法以糾正上述錯誤.

2.2.2 MRR2 方法

MRR2 方法是Mays 等[22]通過改進MRR1 方法獲得一種新的半參數方法.與MRR1 方法比較而言,MRR2 方法在建模組合策略上有所不同.第一,MRR2 方法將對參數方法得到的殘差進行非參數處理,得到非參數殘差部分.然后,將非參數殘差部分和參數擬合部分進行組合.第二,MRR1 將非參數和參數部分各自設定未知的權重系數,權重和為單位1.而MRR2 方法則將參數擬合部分權重賦值為1,非參數殘差部分權重用混合參數λ(λ ∈[0,1])表示.在MRR2 方法中,參數擬合也是利用最小二乘方法進行擬合;非參數方法則是對參數擬合與真實響應值的殘差進行非參數擬合.所謂參數擬合和真實響應的殘差是指參數擬合無法獲取的數據結構,而本節的非參數擬合是指通過LLR 來對上述殘差進行擬合,其混合模型為

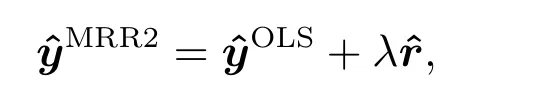
類似于MMR1 中的λ的求法,λ ∈[0,1],λ的大小并不像上一節方法可以反映模型錯誤估計的程度,而是指表示殘差擬合需要的校正量.當λ= 1 時表示非參數擬合和參數擬合所占的比重一樣.漸近最優估計的λ表達式為根據以往文獻發現,關于響應估計的期望,一般認為MRR2 的效果比MRR1 的效果更加好.因此,本文將傾向于使用MRR2 方法進行參數估計.

3 本文所提方法

3.1 考慮重復試驗的非參數響應曲面建模

在多響應優化設計中,若無法根據試驗設計數據獲得響應曲面模型的結構時,采用傳統的參數回歸方法進行均值響應曲面建模則可能會引起較大的偏差,即造成較大的模型誤差.鑒于上述情況,引入非參數方法來構建響應與試驗因子之間的響應曲面模型,其具體模型為

其中響應預測值是由非參數擬合部分h(xi)和誤差部分εi組成,其中εi ～N(0,1).

若試驗在每個處理(即試驗方案)下都存在重復試驗時,可以借鑒雙曲面建模思想利用非參數方法來構建基于響應均值和方差的雙響應曲面模型.結合上一節的非參數響應曲面建模知識,本文選擇相對簡單的局部多項式回歸非參數方法,其中核函數選擇常用的高斯核函數κ(u)=e?u2.上述核函數的帶寬b可以利用式(2)通過最小化PRESS??來獲得.

針對具有重復試驗數據的多響應優化問題,利用非參數模型(即式(9))來分別擬合各響應方差以及這些響應之間的協方差與試驗因子x的函數關系.在此基礎上獲得響應方差–協方差函數Σy(x)與試驗因子x之間的關系.另外,利用重復試驗數據獲得每個試驗點的樣本均值,然后利用非參數模型即式(9)擬合響應均值與試驗因子之間的響應曲面模型,即均值函數E[y(x)].在此基礎上,利用多響應的質量損失函數構建本文所提方法的優化模型,即

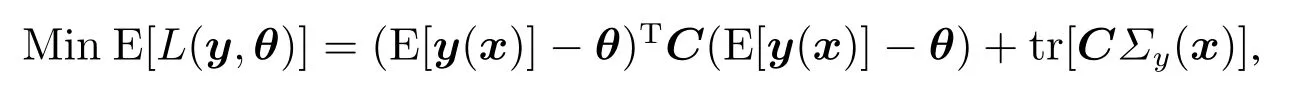
其中θ代表目標值矩陣,C代表成本矩陣.

具體的非參數響應面方法的步驟如下:

步驟1根據PRESS??函數代碼迭代從候選列表中找出最優帶寬值b.

步驟2代入期望質量損失函數,利用遺傳算法參數優化,得到最佳參數水平值.

步驟3部分試驗結果會受到噪聲因子的影響使得結果的可靠性降低.為了對結果的可靠性評估,利用隨機抽樣(蒙特卡羅抽樣),統計落在規格限內的樣本數目,從而能夠評估優化結果的可靠性.

3.2 結合貝葉斯抽樣技術的誤差修正模型

有重復試驗數據的情況下,基于半參數方法的多響應曲面模型一般可假設為

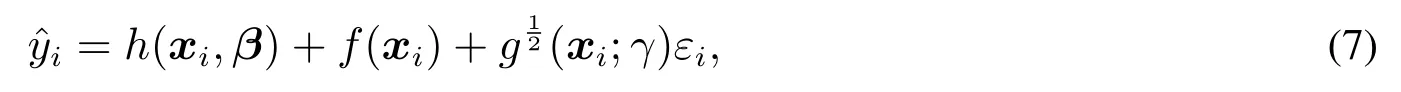
其中h(xi,β)代表參數方法部分,f(xi)代表的是非參數部分,是對方差模型的轉換,εi是指隨機誤差.

然而上述做法存在三個不足之處: 一是重復試驗成本較高;二是試驗數據的隨機誤差假設服從標準正態分布即εi ∈N(0,1)可能與實際情況并不相符,無法真實地反應模型隨機誤差的分布特征;三是上述模型僅僅在具有重復試驗數據情況才能構造出方差模型.若試驗數據沒有重復的情況下,則需要進一步考慮如何構造合適的統計量來刻畫響應曲面模型的隨機誤差部分.

借鑒參考文獻[13]中利用貝葉斯抽樣方法獲取隨機誤差項的思想,本文將對式(7)中的隨機誤差項進行修正,其具體模型為

其中W ∈N(0,H?1),v=N ?p ?q+1,H=在式(12)中,其隨機誤差項為

在此,本文擬結合半參數建模思想和貝葉斯抽樣方法,將式(8)中Bz(x)運用式(7)中半參數方法進行擬合.上述處理方法能夠充分利用半參數方法的優勢,如能夠有效地處理小樣本試驗數據等.需要特別指出的是,式(11)中隨機誤差項將在新模型中用式(12)的隨機誤差項所替代.利用貝葉斯抽樣技術進行誤差修正后的響應曲面模型為

其中v是自由度,N是樣本大小,W是一個具有零均值向量和方差協方差矩陣為H?1的多元正態隨機變量.z(xi)是觀測點的q×1 的觀測值,其中X是二階因子模型矩陣,Y是N ×p響應值矩陣.?B是擬合系數向量,Z是由N個z(xi)向量形成的q×N矩陣.U是一個自由度為v不依賴于W的卡方隨機變量.

在上述響應曲面模型的框架下,結合雙響應曲面建模思想[25]分別構建出響應均值和方差模型,然后利用多元質量損失函數獲得期望目標函數為

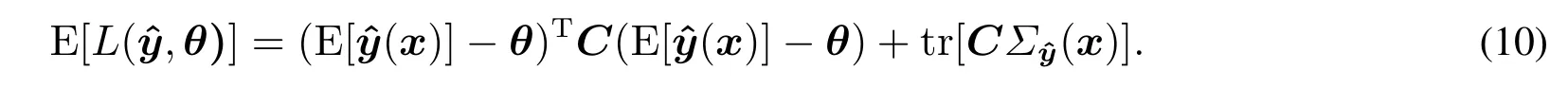
式(10)本質上是采用組合建模的思想所構建的一種新模型.該模型整合了試驗者根據經驗所設定的參數模型與適應試驗數據特點所估計的非參數模型二者的優勢.在此基礎上,利用貝葉斯方法對模型誤差的修正則進一步提升了所構建模型的預測能力.此外,該模型還兼容了半參數方法和貝葉斯方法的特點,能夠有效地處理小樣本試驗數據的問題.因此,與以往的研究方法比較而言,基于數據驅動建模思想的響應曲面模型,能夠更好地提取試驗數據的特征,構建更為精確、更加符合實際的響應曲面模型.

3.3 基于混合遺傳算法的參數優化

由式(7)～式(10)可知,結合半參數方法和貝葉斯抽樣方法所構建的響應曲面模型往往具有高度復雜的非線性特征,傳統的優化方法(如線性規劃、梯度優化等)將難以獲得可靠的優化結果[28].為此,借鑒文獻[1,13],利用結合遺傳算法和模式搜索法的混合遺傳算法對上述目標函數即式(10)進行參數優化.與傳統的優化方法比較而言,混合遺傳算法有效地利用遺傳算法良好的全局搜索能力和模式搜索方法突出的局部優化能力,因此利用該方法能夠有效地處理高度復雜的參數優化問題[29].

3.4 評估優化結果的可靠性

在多響應曲面優化設計中,由于模型不確定性以及隨機誤差等因素的影響,將會導致輸出響應呈現出相當大的波動.在這種情形下,如何衡量預測響應波動對優化結果的影響,如何評估優化結果的可靠性成為一項亟待解決的研究課題.為此,一些研究者提出一些評估優化結果可靠性的研究方法.其中,最具有代表性的是貝葉斯后驗概率方法[11].該方法的核心思想是在貝葉斯響應曲面建模框架下,利用貝葉斯抽樣方法計算預測響應值(即在最優參數設計值下的響應預測結果)落在其規格限內的概率,從而據此度量優化結果的可靠性.在給定的試驗數據data 和響應規格限A下,其最優參數設計結果的貝葉斯后驗概率的計算式為

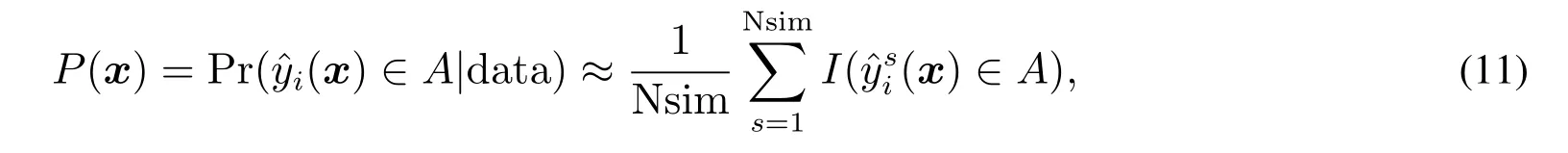
其中Nsim 代表響應模擬抽樣次數,I(·)為示性函數.

當響應模擬抽樣值落在規格限內時其后驗概率結果P為1,否則為0.

在多響應優化設計中,在試驗響應個數較多時,式(11)將是一個非常復雜的高維數值積分問題.此外,在很多情況下,其響應的密度函數往往非常復雜,甚至難以直接獲得.因此,在這種情況下,通過貝葉斯模擬抽樣方法將會大大地降低問題的難度和計算的工作量.需要特別指出的是,上述貝葉斯后驗概率方法不僅適用于單響應參數優化問題,而且也可以拓展到多響應曲面的參數優化問題.在多響應優化設計中, 通過式(11)不僅可以獲得單個響應預測值的邊際后驗概率值,而且也可以獲得多個響應預測值落在其對應規格限內的聯合概率概率值.

3.5 本文所提方法的實施步驟

針對多響應曲面優化設計中存在的問題,本文結合半參數方法和貝葉斯抽樣模擬技術,提出一種新的建模與優化技術,其具體的實施步驟如下:

步驟1首先對原始數據進行普通最小二乘法(OLS)擬合分別得到關于兩個響應的參數擬合值,然后通過原始響應構建殘差向量,將殘差向量再利用PRESS??函數尋求最佳的帶寬值b.

步驟2根據半參數模型公式中的非參數部分,利用LLR 方法對上述步驟2得到的兩組殘差向量分別進行非參數擬合得到兩組非參數擬合的擬合殘差向量.

步驟3通過步驟1 和步驟2 中分別得到的OLS 擬合值和非參數殘差擬合值.利用MRR2 方法中的混合參數構造方法——函數,分別得到對應響應的最合適的混合參數值λ.結合OLS 擬合值、殘差擬合值和混合參數λ將非參數響應曲面模型擴展為半參數響應曲面模型.

步驟4借鑒參考文獻[13]中利用貝葉斯抽樣方法獲取隨機誤差項的思想進行誤差修正,同時利用半參數的響應建模方法對響應曲面進行重新擬合.最后,綜合上述兩個方面的改進提出一種基于誤差修正的響應曲面模型,并在此基礎上利用多元質量損失函數構建出本文所提方法的優化目標函數.

步驟5利用混合遺傳算法對步驟4 中所獲得期望質量損失函數進行參數優化,獲得最優的參數設計值.

步驟6利用貝葉斯后驗概率方法對參數優化結果的可靠性進行評估.

4 實例分析

該實例來源于文獻[13],其主要目的是對一種聚合物進行參數優化設計,以尋找最佳的設計參數值.在該試驗中,可控因子為反應時間x1(reaction time)、反應溫度x2(reaction temperature)和催化劑的用量x3(amount of catalyst).試驗的輸出響應是轉化率y1和熱活動y2.其中,轉化率為望大類型的質量特性(y1∈[80,100]),目標值θ1假定為100;而熱活動為望目的質量特性(y2∈[55,66]),其目標值θ2假定為57.5.在整個試驗的分析過程中,假設回歸模型中因子效應所構成的向量為z(x) = (1,x1,x2,x3,x1x2,x2x3,x1x3,x21,x22,x23).在該試驗中,試驗者選擇中心復合設計(central composite design,CCD)開展相關的試驗,其聚合物試驗的因子計劃安排、響應的輸出結果如下表1 所示.

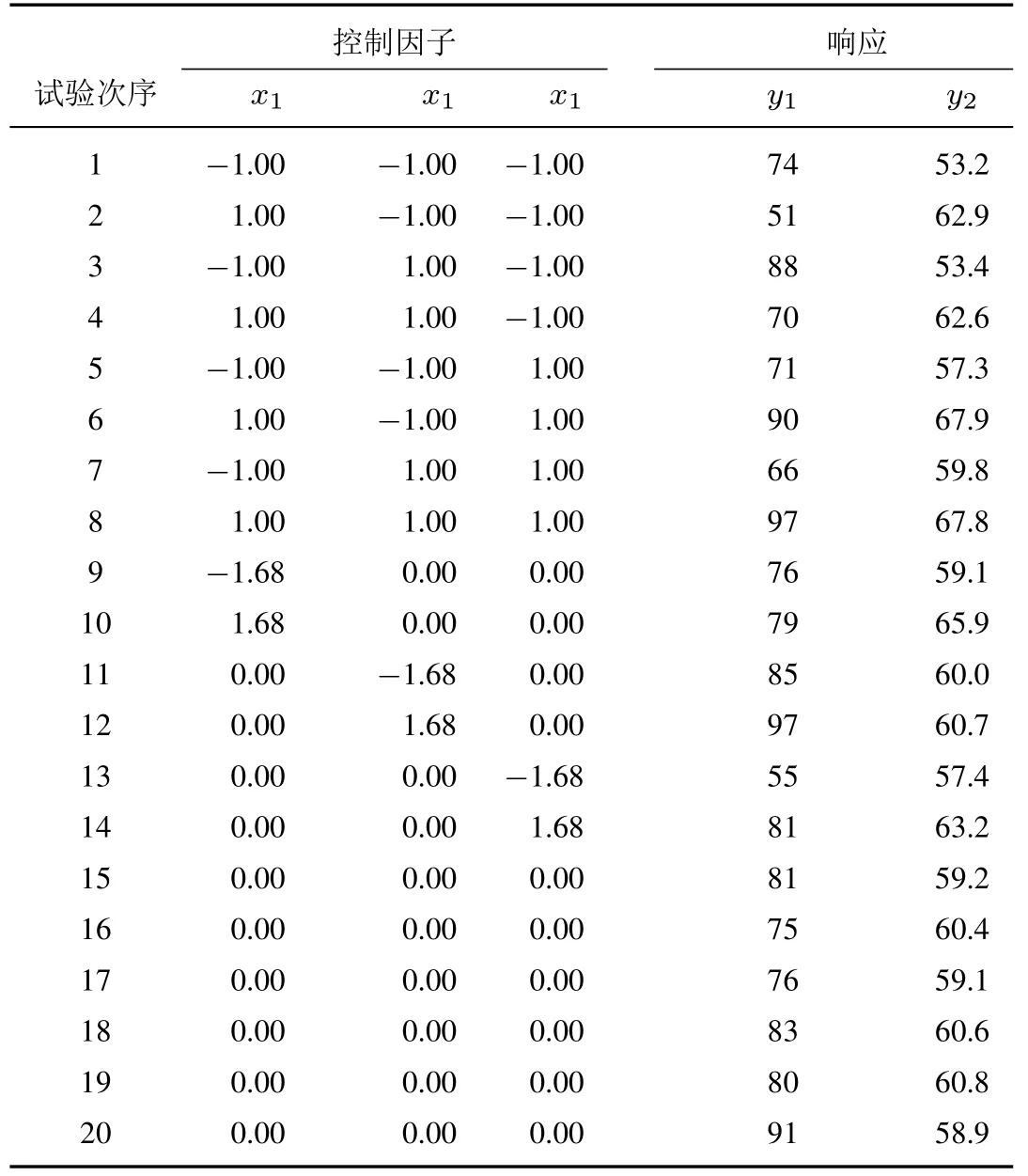
表1 某聚合物的試驗設計結果Table 1 The experimental design results of a polymer

根據第3.5 節中所提出的實施步驟,結合上述表1 所獲得可控因子與輸出響應的試驗數據,在此利用半參數建模方法進行響應曲面建模.其中非參數方法中核函數選擇為高斯核函數,其最佳帶寬值b(其中兩個響應關于帶寬的PRESS??函數如圖1,圖2 所示)分別為0.68 和0.35,最佳混合參數值為1.

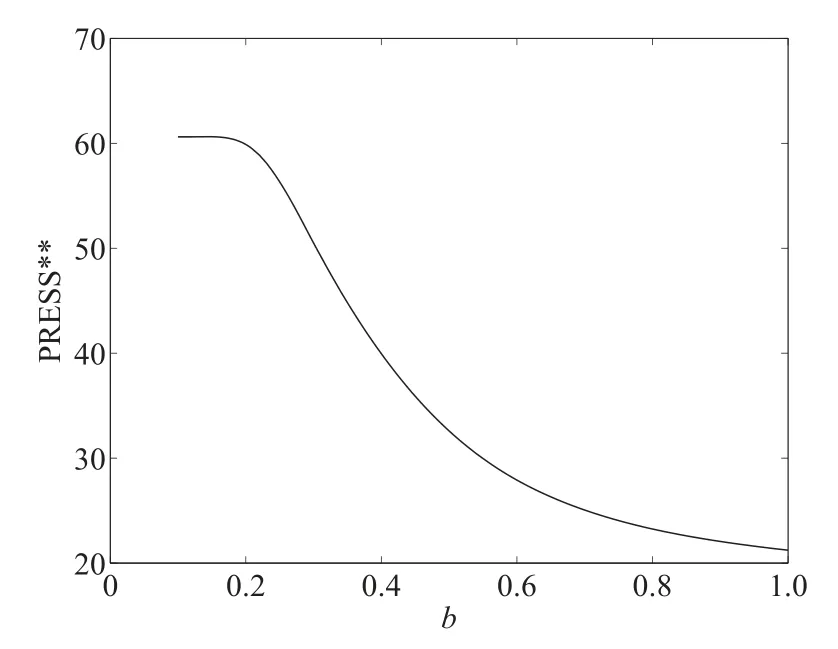
圖1 響應值y1 的PRESS??函數圖Fig.1 PRESS??function diagram of response y1

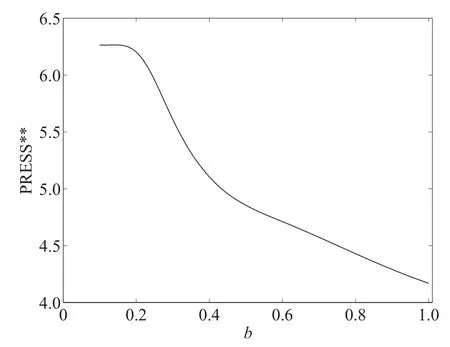
圖2 響應值y2 的PRESS??函數圖Fig.2 PRESS??function diagram of response y2

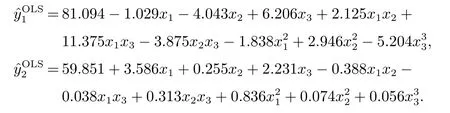
然后,利用第3.3 節中所介紹的混合遺傳算法對所提出的期望質量損失函數進行參數優化,其參數優化結果為x1=?0.050,x2=1.682,x3=?0.063.同時,在最優位置點處的期望質量損失為13.834,貝葉斯后驗概率為0.813 8.若采用文獻[13]方法對該聚合物試驗進行分析可知,其期望質量損失函數為14.663 6,同時其貝葉斯后驗概率(即蒙特卡洛的抽樣值落在給定規格限內的概率)為0.602 8.與文獻[13]研究結果比較而言,本文所提方法在期望質量損失和后驗概率值(該指標反映產品符合規格的程度)均表現出一定的優勢,其主要原因是文獻[13]方法事先假設固定的模型結構,從而忽視模型結構不確定性對優化結果的影響.正如文獻[13]中曾指出的那樣,模型結構的變化可能會低估或高估其綜合性能評價指標(如期望質量損失函數或貝葉斯后驗概率).此外,為了進一步驗證所提方法的有效性,本文還將文獻[11]的貝葉斯后驗概率方法、文獻[10]的多元質量損失函數方法、文獻[20]中提到的非參數、文獻[20]中提到的半參數方法運用到該聚合物試驗的參數優化過程中,其優化結果如表2 所示.與文獻[20]中的非參數方法和半參數方法兩種方法比較而言,本文所提方法在期望質量損失函數和規格限內的概率兩個評估指標上均優于上述兩種方法的優化結果.因此,本文所提方法不僅在期望質量損失方面有所降低,而且在考慮產品的符合性概率方面也獲得了較大的提升.

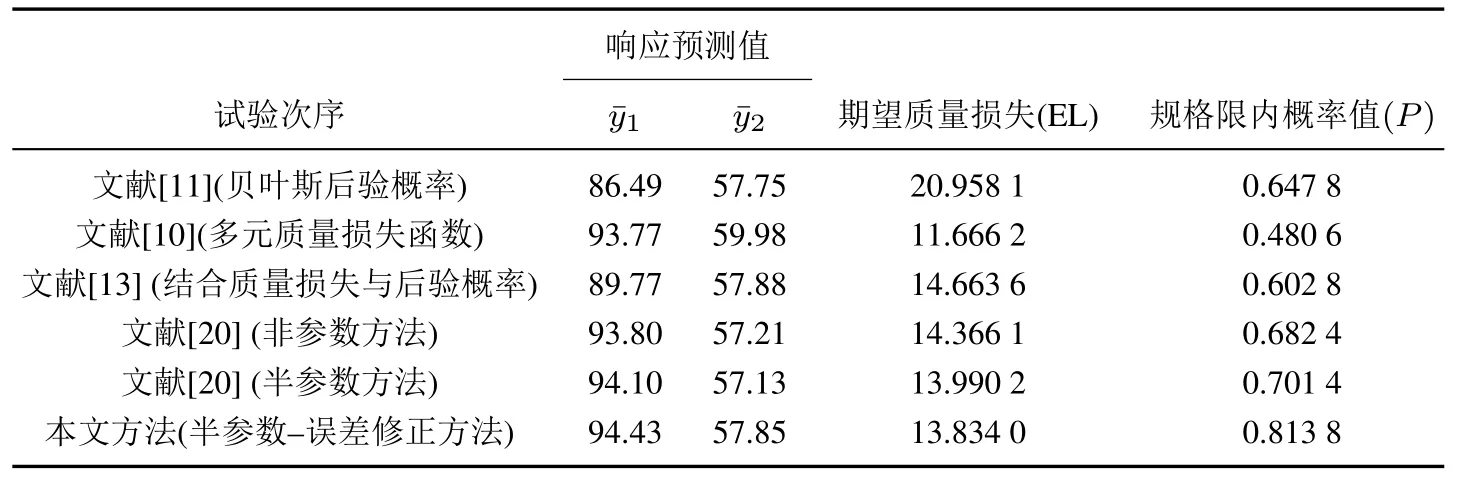
表2 優化結果指標對比表Table 2 Comparison table of optimization results

此外, 為了進一步驗證參數優化結果的可靠性, 在最優參數設計值下利用所構建的響應模型進行10 000 次隨機模擬抽樣.考慮到樣本間的自相關性,每間隔4 個抽樣點抽取一次,最后獲得了2 000 次的響應抽樣值,其兩個響應y1和y2抽樣值的蹤跡圖如圖3 和圖4 所示.

在圖3 中,其兩條紅線分別代表響應y1的規格上限100 和規格下限80.由于響應y1為望大類型的,因此其響應目標值假設為100,目標值紅線和上限紅線重合.另外,在圖4 中,其響應y2的規格上限和下限分別為55 和66.圖4中間的紅線代表響應y2的目標值,即為57.5.從圖3 和圖4 可知,由于隨機誤差等確定性因素的影響,上述兩個響應的抽樣值圍繞著某個確定的均值呈現上下隨機波動的趨勢,且其波動幅度基本保持一致,呈現出穩態分布的特征,因此可以利用其響應抽樣值來評估其參數優化結果的可靠性.根據上述抽樣結果,可以計算得出兩個響應抽樣值落在其對應的規格限內的概率分別為0.845 2 和0.956 6.上述的研究結果進一步證實參數優化結果的可靠性.

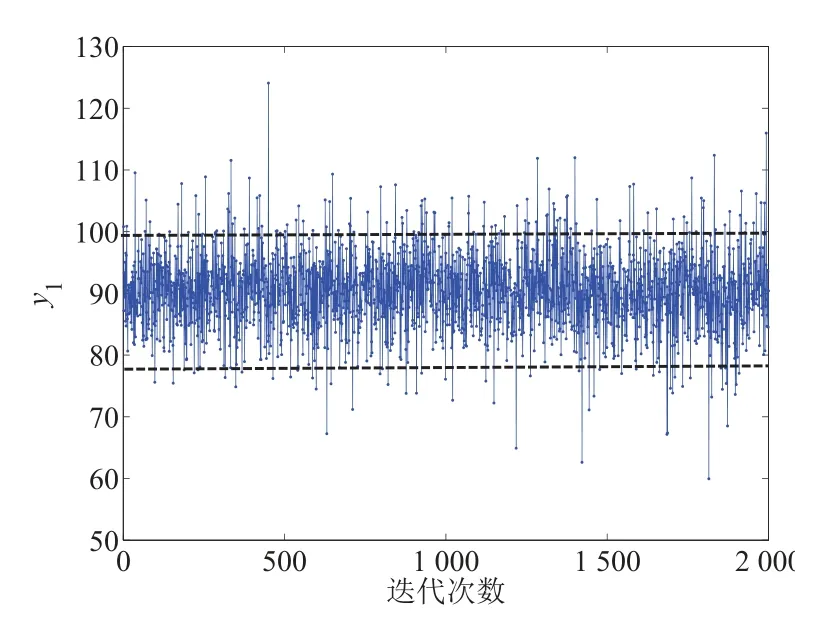
圖3 響應值y1 的軌跡圖Fig.3 Trace plot of response value y1

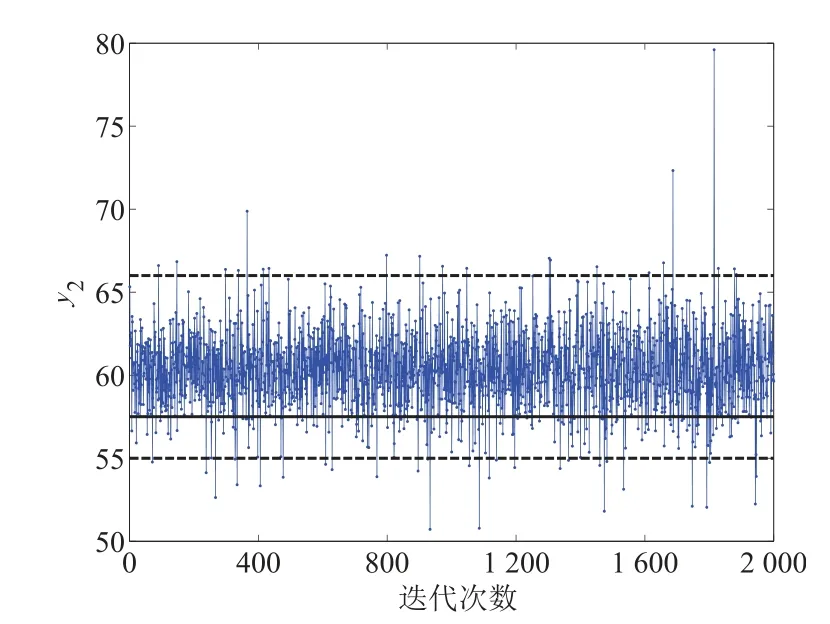
圖4 響應值y2 的軌跡圖Fig.4 Trace plot of response value y2

5 結束語

本文利用半參數方法建立過程響應與可控因子的響應曲面模型,并在此基礎上結合貝葉斯抽樣方法對所構建的響應曲面模型進行誤差修正,從而獲得更加精確、更加符合實際情況的響應曲面模型.此外,本文還利用貝葉斯后驗概率方法進一步地評估了參數優化結果的可靠性.需要特別指出的是,若根據工程背景或專家知識能明確給出響應曲面模型結構時,則使用參數回歸方法往往能夠獲得理想的模型估計結果.然而,若模型結構無法確定,則采用非參數或半參數方法等數據驅動方法往往能夠獲得更為可靠的響應曲面模型.

此外,未來的產品質量設計還需要從產品全生命周期視角全面地分析與思考.例如,在產品設計階段,考慮通過互聯網讓廣大客戶參與產品質量設計,讓所制造出的產品全面反映客戶需求,真正做到高度客戶化;在產品生產階段,考慮利用物聯網與傳感器、以及人工智能技術,對生產過程進行實時質量監控與反饋,及時采集生產過程中環境(如溫度、濕度)、設備故障等數據信息,然后利用大數據分析技術對所收集到的上述數據進行全面地分析,探尋可能影響最終產品設計質量的關鍵因素并加以優化;在產品售后以及使用階段,充分地利用互聯網或物聯網及時收集客戶在使用中所發現的潛在質量問題,或客戶在維修保養過程中存在的產品質量問題,然后結合大數據分析技術尋求潛在的原因,并在未來產品質量設計中逐步加以改進和完善[30].因此如何結合互聯網、人工智能與大數據分析技術開展產品質量設計技術與方法將是未來有待進一步研究的重要課題.