基于可信性的二維二元語義多屬性群決策方法

伊長生, 牛家強, 潘瑞林

(安徽工業大學管理科學與工程學院,安徽馬鞍山 243032)

1 引 言

隨著社會經濟的快速發展和事物本身的復雜性加劇,多屬性決策問題在社會、經濟、文化以及企業的生產運營管理等領域得到了廣泛應用,如復雜產品協同開發的供應商選擇問題[1],醫療服務機構的滿意度測評[2],設備開發方案的選擇問題[3]等.而多屬性決策過程,實質上就是決策者在一組具有一定屬性的備選方案中選出最優方案的過程,這些屬性可能是定量的也可能是定性的.然而在現實的多屬性決策過程中,考慮到信息本身的自然屬性以及人類思維的主觀性和模糊性,決策者往往不能精確地以量化的形式給出評價信息,只能粗略地以定性的語言短語的形式給出評價信息.為此,Zaheh[4]最先提出了用語義變量(如“差”、“一般”、“好”等)來給出評價信息,使得表達更加符合決策者的意識.基于此種方法,已有學者提出了一些相關的語言運算模型[5,6],但這些模型存在著運算結果常常與事先定義的語言評價集中的元素不一致的問題,只能近似地用語言評價集來代替.為了解決此類信息缺失和運算結果不精確的問題,Herrera 等[7]提出了二元語義分析模型,并在實際決策問題中得到了廣泛應用.近年來,學者們針對二元語義模型展開了多種形式的擴展研究.比如,Wang 等[8]基于“符號比例”的概念提出了比例二元語義模型;張永政等[9]提出了基于二元語義和D 數的語義評價信息表達;黃必佳等[10]通過綜合應用語義標度提出了基于TOPSIS 和二元語義的LTOPSIS-2T 模型;黃海燕等[11]基于區間復合標度考慮了個人喜好差異,提出一種新的二元語義模型.

然而,單純的二元語義模型僅考慮到決策者對決策對象本身的評價,而忽略了評價結果的可靠性程度,這在某種程度上會影響初始決策信息的準確性.因此,朱衛東等[12]提出了二維語言信息,在傳統二元語義模型的基礎上增加了一維表示專家判斷可靠性程度的第二維語言信息,使得利用該模型表達語言評價信息時更加可靠準確.正是由于二維語言信息在語言表達上更加準確,關于二維語言多屬性決策方法的研究逐步成為學術界研究的焦點問題.具體研究可以分為兩類: 其一是針對二維語言信息表達的量化研究.張晨等[13]通過證據推理原理給出了二維語言識別框架,進而定義了基于證據推理的二維語言信息.Zhu 等[14]提出了一種用于二維語言運算和表達的格蘊涵代數,以此達到使二維語言信息更易于理解的目的.其二是針對二維語言算子的研究.二維語言有序加權算子[15]以及依賴型集結算子[16]被相繼提出并應用于二維語言多屬性決策問題.Liu 等[17]在二維不確定性語言信息[18]的基礎上進行了深一步研究,定義了二維不確定性語言Power 算子.Liu[19]提出了基于擴展TOPSIS 的二維不確定性語言群決策方法.

基于上述分析,為了充分發揮二元語義模型的靈活性、精確性以及二維語言信息在初始決策意圖表達上的準確性,尤其是多屬性群決策中對兩個維度信息的處理問題,有必要進一步拓展關于二維二元語義群決策方法的研究.目前,關于二維二元語義群決策方法的研究少之又少,研究成果甚是匱乏,而且現有的相關文獻也存在一定程度的不足之處.比如,吳良剛等[20]提出改進的二元語義模型,定義了二維二元語義及其加權平均算子,但所采用的語言評估標度并不合理,而且二維二元語義期望值函數,其實質只是將一、二維語言信息簡單的相乘,并沒有考慮到第二維語言本身所存在的意義.王澤林[21]提出了一種新的關于二維二元語義的比較方法和距離公式,進而給出了權重信息完全未知的二維二元語義多屬性群決策方法,其中的信息重要程度比例系數并不能通過精確的計算得出,只能人為設定,主觀性較大.

針對二維二元語義群決策研究中存在的信息處理不精確問題,本文提出一種基于可信性測度的二維二元語義群決策方法.考慮到非平衡語言標度更加符合決策者的心理判斷,提出了一種基于正態分布的二元語義模型.考慮到第二維語言本身所具有的意義,利用可信性測度[22]提出了一種確信度函數,進而構建了新的二維二元語義期望值函數和距離函數.根據決策者和各屬性的相應權重求出備選方案的最終期望值,進而對方案進行排序.通過一個可再生能源選擇的算例分析驗證了該方法的可行性和科學性,并對決策結果進行了敏感性分析,分析結果表明該排序方案具有顯著的魯棒性.

2 二維二元語義表示模型

2.1 二元語義

Herrera 等[7]提出的二元語義模型能有效避免信息失真和提高計算準確性.下面給出二元語義的定義.

定義1[7]設S={s0,s1,...,sg}是一個語言評價集,S中的語言評價值經過某種集結方法得到的實數為θ ∈[0,g],則θ對應的二元語義信息可由如下的函數Δ表示,即

其中round 表示“四舍五入”算子,si表示語言評價集S中的第i個元素,αi=θ ?i,稱為符號轉移值.

該定義可以由圖1 作進一步說明[23],其中語義變量S介于s5和s6之間,則可用二元語義表述為(s5,α).

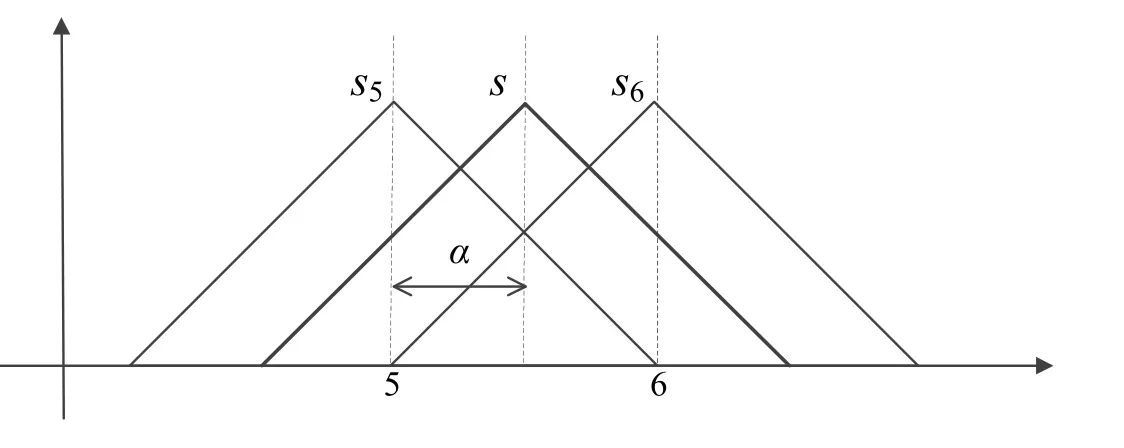
圖1 二元語義變量Fig.1 Variable of 2-tuple linguistic information

定義2[7]若存在一個二元語義(si,αi),則與其相對應的實數值θ可由一個逆算子Δ?1轉換而得,即

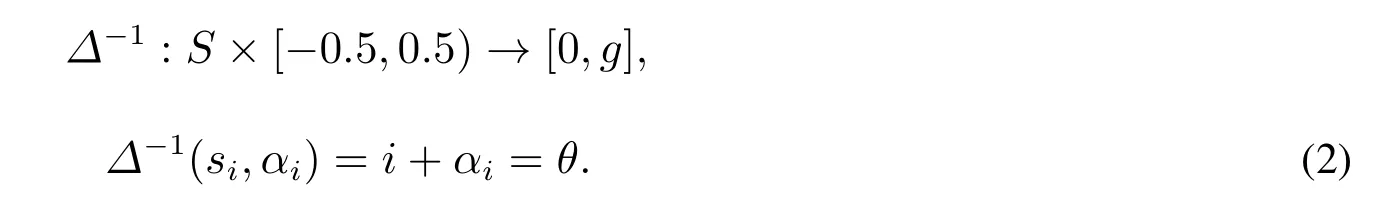
2.2 二維二元語義

二維二元語義包括兩種常見的語言評價集, 其中第一個維度, 如S={s0= 特差,s1= 很差,s2=差,s3= 較差,s4= 中等,s5= 較好,s6= 好,s7= 很好,s8= 特好},是用于表征決策者給出的關于備選方案本身的評價結果; 第二個維度, 如C={c0= 很沒把握,c1= 沒把握,c2= 一般,c3= 有把握,c4=很有把握},是用于表征決策者對給出評價結果的可靠性的自我評價[12].二維二元語義較之一維二元語義能夠對具有不確定語言信息的備選方案進行更為精確的評估.下面給出二維二元語義的定義.

定義3[21]假設存在兩個語言評價集S={s0,s1,...,sg}和C={c0,c1,...,ck},則=〈(sit,αit),(cjt,αjt)〉為一組二維語言變量,其中sit ∈S,cjt ∈C,αit,αjt ∈[?0.5,0.5).

定義4[21]設=〈(sit,αit),(cjt,αjt)〉,t= 1,2,...,n為一組二維二元語義變量,與其相對應的權重向量為W=(w1,w2,...,wn)T,wt ∈[0,1]且=1,則二維語言加權平均算子為

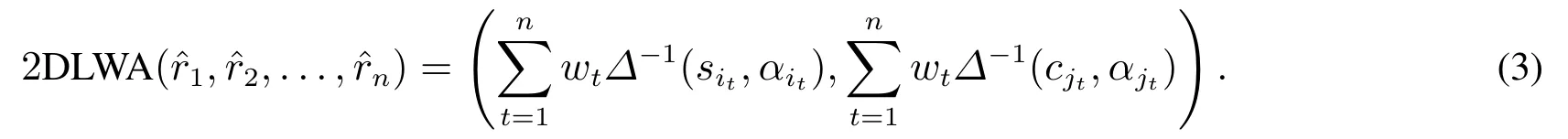
2.3 可信性測度

可能性測度、必要性測度和可信性測度為模糊數學中三種相對重要的測度[22],而可能性測度以往總被人們看作是與概率測度對等的概念.實際上,可信性測度才是在模糊數學中充當著概率測度的角色.可信性測度的定義以及相關性質如下.

定義5[24]假定Θ為一非空集合,P(Θ)是集合Θ的冪集,則對于P(Θ)中的任一模糊事件A都有一實數值Cr{A}表示其可信性測度,同時Cr{A}必須滿足以下4 條性質.

性質1Cr{Θ}=1.

性質2當A ?B時,Cr{A}≤Cr{B}.

性質3Cr 具有自對偶性,即對任意A ∈P(Θ),總有Cr{A}+Cr{Ac}=1,其中Ac為A的對立事件.

性質4對于任意Cr{Ai}≤0.5 的事件Ai,都有Cr{∪i Ai}=sup為上界.

定義6[24]假設Θ為一非空集合,它的冪集為P(Θ),Cr 表示可信性測度,則三元組(Θ,P(Θ),Cr)稱為可信性空間.

定理1[24]設ξ是可信性空間(Θ,P(Θ),Cr)上的一個模糊變量,t為任一實數,則模糊變量ξ的隸屬度函數可以通過以下的可信性測度公式導出

據此,有可信性測度的反演定理.

定理2[24]若模糊變量ξ的隸屬函數為μ,則對于任何一個實數集A均有

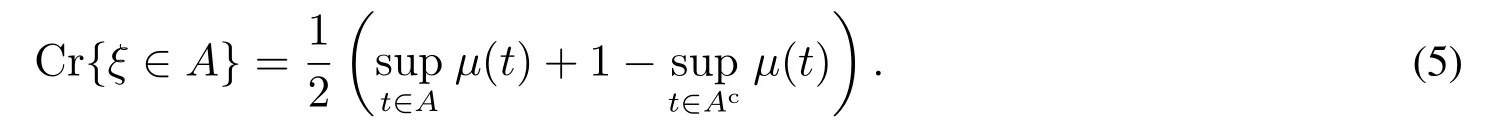
2.4 基于正態分布的二元語義模型

本文給出基于正態分布的二元語義表示模型,在此基礎上提出新的二維二元語義距離函數和期望值函數,并據此構建基于可信性測度的二維二元語義表示模型.

2.4.1 基于正態分布的語言評估新標度

Pei 等[25]提出了四類基于正態分布的不均勻尺度集.考慮到合理的語言尺度集應包括好與壞兩個方向,并且是關于中間值對稱分布的;此外,隨著標度值的下標絕對值的增加,標度值應變得越來越稀疏.所以,本文選取第一類語言尺度集作為語言評估標度.基于正態分布N(0,σ2)的語言尺度集的相關定義如下.

定義7[25]假設語言尺度集S={s?i,s?(i?1),...,s0,...,si?1,si},i= 1,2,...,n,則正語言尺度值可以由下式得到,即

其中Φ?1代表累計概率分布函數Φ的逆函數.同理,根據正態分布的對稱性原則,當i<0 時也可根據式(6)求出相應的語言尺度值.

例1取σ= 1,i= 4 時, 有S={s?4= 極差,s?1.15= 很差,s?0.675= 差,s?0.32= 較差,s0=一般,s0.32=較好,s0.675=好,s1.15=很好,s4=極好}.

在該語言標度中,相鄰語言標簽下標之間偏差的絕對值隨著語言標簽值的增大而增大.德國心理學家費希納也曾提出了著名的韋伯–費希納定理[26],即Ψ=κlg?,其中Ψ為人的主觀感覺量,?為客觀刺激強度,κ為韋伯常數.當刺激大小在以幾何級數上升時,感覺的量值在以算術級數上升.由此可見,該語言標度是合理的,并且符合專家的心理判斷和對客觀刺激的主觀感受.

2.4.2 基于新標度的二元語義模型

基于文獻[25]的語言評估尺度集,提出語義度量函數φ(si),φ(si)→δ(i)∈[?4,4],其中

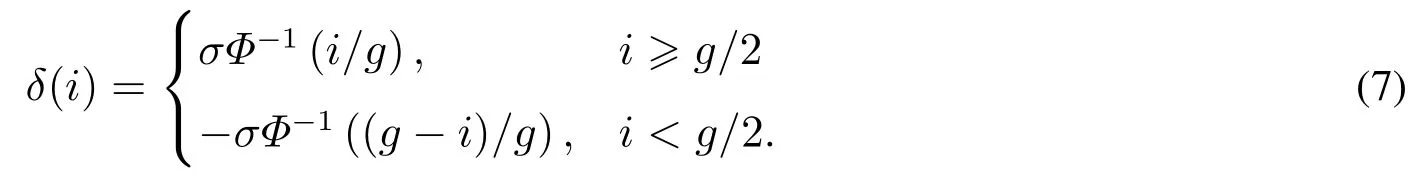
下面給出改進后的二元語義模型及其相關的定義.

定義8設S={s0,s1,...,sg}為一組語言評價集,其中si ∈S,i= 0,1,...,g,實數θ ∈[?4,4]為S中的語言評價值通過某種集結方法得到的結果,則與實數θ相對應的二元語義值可以通過函數Δ獲得,

即Δ:[?4,4]→S×[?0.5,0.5),

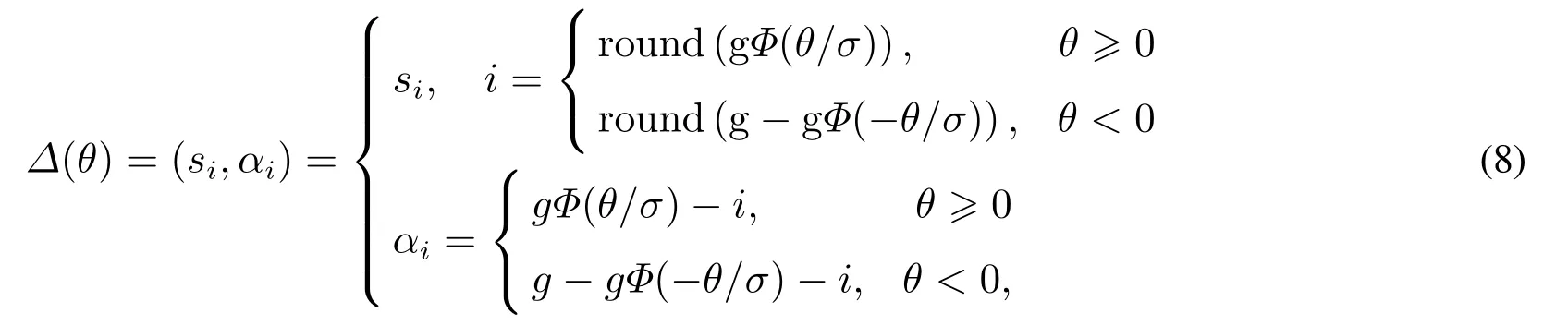
其中αi ∈[?0.5,0.5),語言評價集S中元素個數為(g+1).

定義9若存在一個二元語義(si,αi), 其中i= 0,1,...,g,αi ∈[?0.5,0.5), 則與其相對應的實數值θ ∈[?4,4]可以通過函數Δ?1得到,即Δ?1:S×[?0.5,0.5)→[?4,4],

2.5 基于可信性測度的二維二元語義模型

當決策者在決策過程中運用二維二元語義變量作為評價信息時,第二維語言評價值是為了表征決策者對自己給出的評價結果的可靠程度大小,即該評價結果的可信性大小.而在決策者自身知識、經驗水平有所保障并且完全理性的情況下,沒有人比決策者更了解自己評價結果的可信性程度,因此,在決策過程中第二維語言評價信息的價值應給予重視.事實上,第二維語言評價值體現了決策者對于第一維語言評價值的不確定性,而這種不確定性如果只用單一的語言評價值來表征,顯然不夠科學也不符合常理,如僅僅只采用“熟悉”、“一般”、“不熟悉”等單一語言評價值來表示對所給出評價結果的可信性程度,明顯存在著決策者“不怎么熟悉也不陌生”的情況.因此,本文基于可信性測度提出一種新的方法來解決上述問題.

令zj表示第一維語言評價值si對評價等級cj的隸屬度,rj= Cr{cj=zj}表示某個模糊事件{cj=zj}發生的可信性測度大小,即表示待評估對象在第一維語言評價集si下的隸屬值zj歸于評語等級cj的可信性測度,其中i=1,2,...,g,j=0,1,...,k.根據可信性反演定理可得

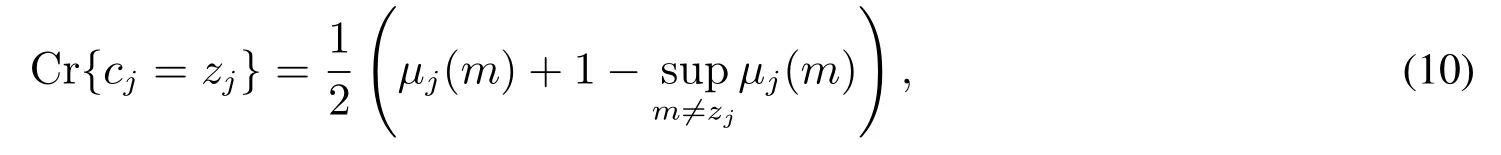
其中μj(m)代表在第一維語言評價值si下m歸于各個語言評價等級cj的隸屬度大小.隸屬值zj可用決策者在各個評語等級cj下自我打分的百分比表示.

設ν為確信度函數,表示對決策者所給出評價結果的可信性程度,ν可由如下公式給出,即

其中cj ∈C,j=0,1,...,k.

例2設第一維語言評價集為S={s0= 特差,s1= 很差,s2= 差,s3= 較差,s4= 中等,s5=較好,s6= 好, s7= 很好,s8= 特好}, 第二維語言評價集為C={c0= 很沒把握,c1= 沒把握,c2=一般,c3= 有把握,c4= 很有把握}.專家E從X1,X2,...,X5五個屬性下分別對備選方案A進行評估的第一維語言評價值為(s6,s5,s4,s5,s5),專家E給出的關于備選方案A評價值的隸屬度如表1 所示.

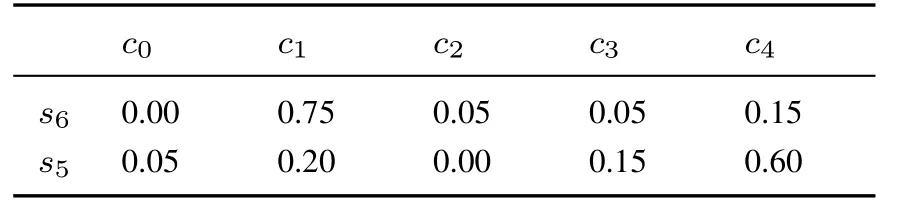
表1 專家E 給出的關于方案A 評價值的隸屬度Table 1 The membership degree of evaluation value of A by E

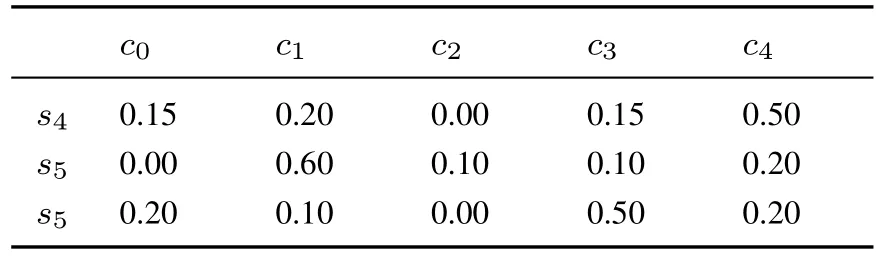
續表1Table 1 Continues

由式(10)計算可得相應的可信性測度為

由式(11)計算可得確信度為ν=(2.350,4.325,4.425,3.150,4.150).

通過例2 可知,在評價信息需采用二維語言表示時,確信度函數可以對第二維語言信息進行準確的量化處理,將決策者對所給出評價結果的把握程度轉化為能夠計算的確信度.將其代入合適的期望值函數中,從而準確地計算出能夠反映決策者真實決策意圖的期望值.

推論1若隸屬度z0=z1=···=zj,j=0,1,...,k,則確信度函數ν退化為語言評價集C的均值.

證明因為隸屬度zj為決策者在各個評語等級cj下自我打分的百分比,故zj明顯滿足以下約束條件

若有z0=z1=···=zj,j=0,1,...,k,根據式(12)可知,必有z0=z1=···=故此時的確信度函數退化為即此時的確信度函數表示語言評價集C的均值. 證畢.

推論2設cj,j=0,1,...,k表示第二維語言評價值,zj表示第一維語言評價值對cj的隸屬度大小,則

證明由式(10)和式(11)可得

從而有

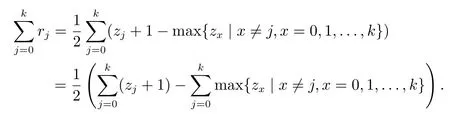
再由式(12)可知0 ≤zj≤1 且=1,故

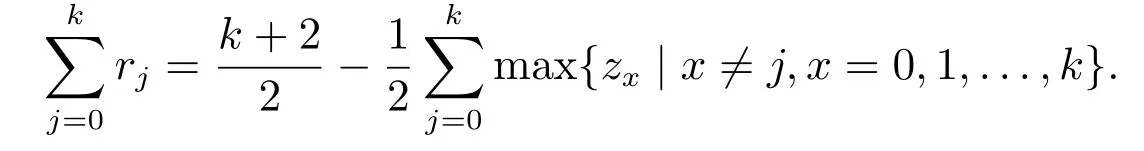
易知max{zx |x=j,x=0,1,...,k} ∈[0,1], 故可得取min{cj}=c0, 可得再取max{cj}=ck,可得. 證畢.

設語言評價集S={s0,s1,...,sg}表示第一維語言信息評價值的集合,C={c0,c1,...,ck}表示第二維語言信息評價值的集合,實數θ ∈[?4,4]為S中語言評價值通過某種方法集結得到的結果,則相應的二維二元語義信息=〈(si,αi),ν〉可通過函數Δ獲得,即

其中i=

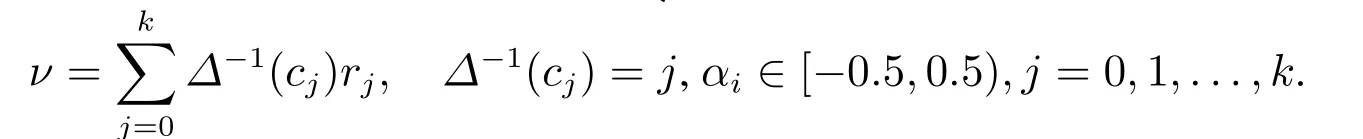
相反,若存在一個二維二元語義〈(si,αi),ν〉,則與其相對應的實數值θ ∈[?4,4]可由函數Δ?1獲得,即

其中θ=

可以證明上述二維二元語義的期望值函數滿足如下性質.

性質1若(sit,αit)相同時,νt越大則相應的二維二元語義越大.

證明當(sit,αit)相同時,由式(15)可知,期望值E[?rt]是關于νt的增函數,故νt越大,則期望值E[?rt]越大,所以相應的二維二元語義越大. 證畢.

性質2若νt相同時,(sit,αit)越大,則相應的二維二元語義越大.

證明當νt相同時,由式(15)可知,期望值函數E[?rt]是關于Δ?1(sit,αit)的增函數.若(sit,αit)越大,那么Δ?1(sit,αit)就越大,故期望值E[?rt]就越大,所以相應的二維二元語義就越大. 證畢.

性質3當νt=1 時,該二維二元語義降為普通的一維二元語義.

證明當νt= 1 時,由式(15)可知,期望值E[?rt] =Δ?1(sit,αit),不難發現此時的二維二元語義的比較就是傳統二元語義的比較,即該二維二元語義退化為一維二元語義. 證畢.

性質4當νt=0時,該二維二元語義信息無效.

證明當νt=0 時,由式(15)可知,期望值E[?rt]為0,即該二維二元語義無效,故性質4 得證. 證畢.

設Vt=〈(sit,αit),νt〉,t= 1,2,...,n為一組二維二元語義, 與其相對應的權重向量為W=(w1,w2,...,wn)T,wt ∈[0,1]且=1,則二維語言加權平均算子為

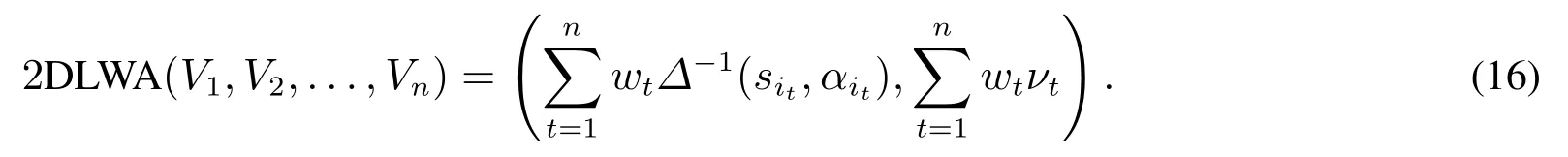
設二維二元語義V1=〈(si1,αi1),ν1〉和V2=〈(si2,αi2),ν2〉,則它們之間的距離為

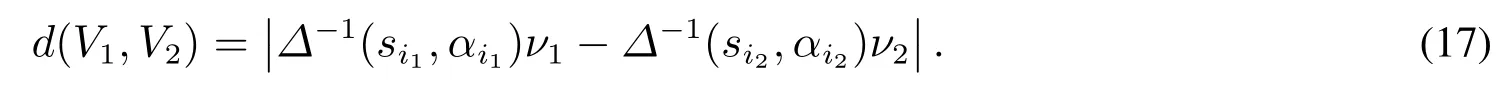
3 二維二元語義多屬性群決策步驟

對于一般的多屬性群決策問題, 假設決策者要從方案集A={A1,A2,...,Am}選出最優方案并進行優劣排序.X={X1,X2,...,Xn}表示需要考慮的屬性集,W= (w1,w2,...,wn)T為屬性權重;E={E1,E2,...,El}表示參與評估的決策者集合,λ= (λ1,λ2,...,λl)T為決策者權重.專家Eh(h=1,2,...,l)針對備選方案Aq(q= 1,2,...,m)的屬性Xp(p= 1,2,...,n)給出的一維語言評價值為構成的一維語言評估矩陣為Dh=()m×n.

步驟1計算專家Eh給出的第一維語言評價值對于第二維語言評價等級的確信度函數.

1)專家給出第一維語言評價值歸于第二維語言評價等級的隸屬度zhqpj.

2)利用式(10)求出模糊事件{cj=發生的可信性測度大小,即

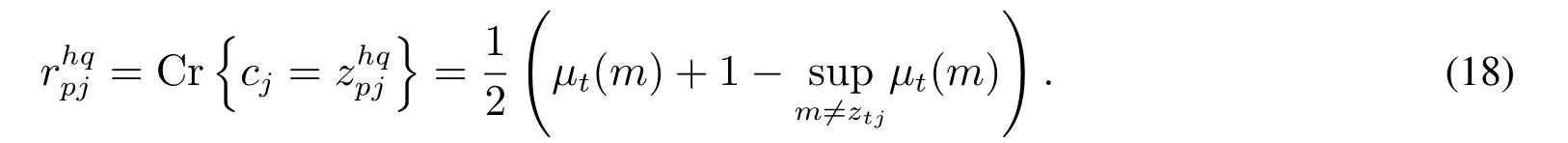
3)根據求出的可信性測度大小,利用式(11)可求得確信度,即

步驟2將專家給出的一維語言評估信息轉化為二維二元語義.

1)對專家給出的一維語言評價值進行標準化處理.

對于成本型屬性cp,將其評價值標準化為=neg();對于效益型屬性cp,將其評價值標準化為=,即

3)構建專家Eh的二維二元語義決策矩陣.

步驟3確定決策者權重.

個體決策者Eh所應占的權重λh可依據個體決策與群體決策之間的差值來計算[27].

λh=為決策者Eh與群體決策之間的差值,h=1,2,...,l.

若該個體決策與群體決策之間的差值越小,則其所應占的權重越大;反之,則其所應占的權重越小.

步驟4 構建綜合決策矩陣.

依據決策者的權重對信息進行集結,形成綜合評價矩陣D= ()m×n.綜合評價值可由二維二元語義加權平均算子求得,即

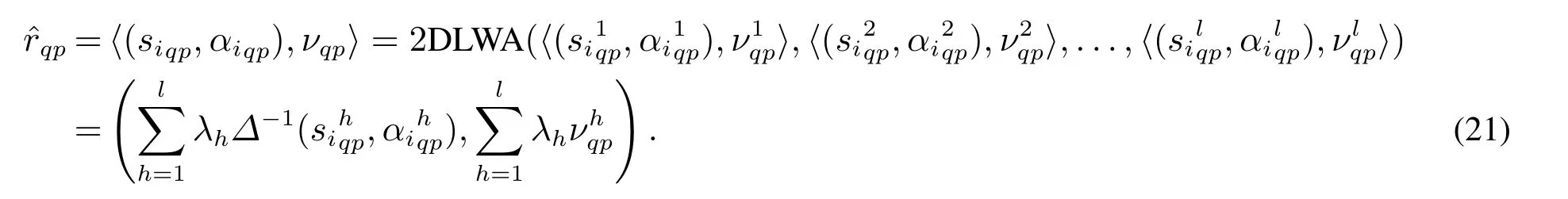
步驟5利用兼顧序信息和強度信息的主客觀組合賦權法求出各屬性的權重.

考慮到主觀賦權法和客觀賦權法各有優劣,而一般的組合賦權法中主客觀權重系數只能靠人為主觀給出,故本文采用文獻[28]中的方法來計算屬性權重,求解下列組合賦權模型以獲得屬性的組合權重,即

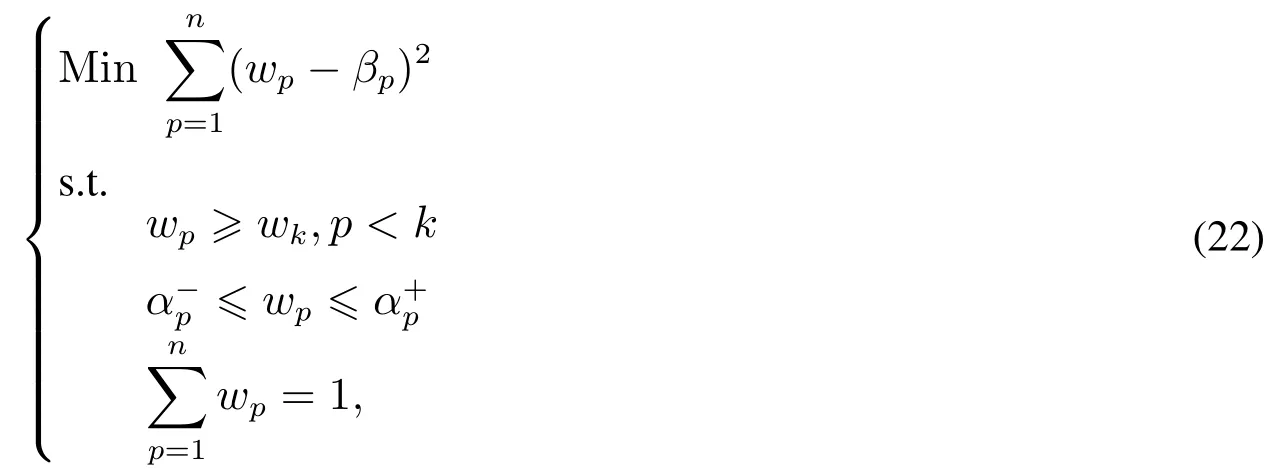
其中wp表示第p個屬性的組合權重,βp表示第p個屬性的客觀權重,表示第p個屬性的組合權重下界,α+p表示第p個屬性的組合權重上界.

步驟6求出最優方案,確定備選方案的優劣排序.

1)利用二維二元語義加權平均算子計算出每個方案下的二維二元語義最終值,即

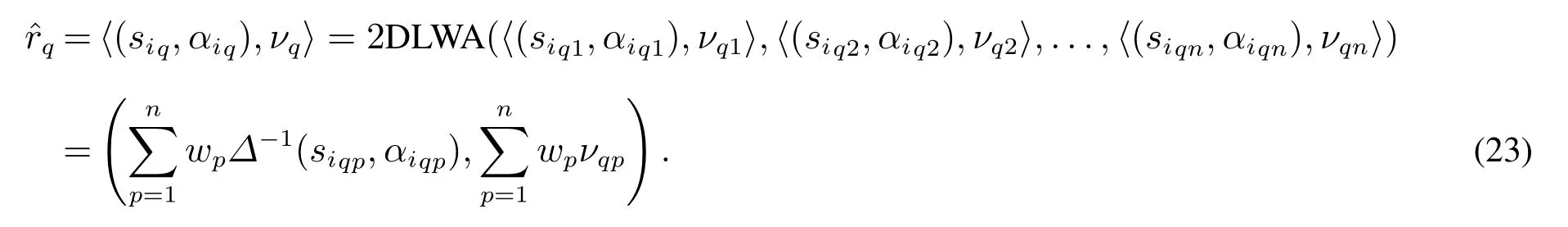
2)根據式(15)可求得各個方案的期望值,即

進而確定優劣順序,選出最優方案.

4 算例分析

隨著化石能源的大規模開采以及工業城鎮化進程的加快,能源枯竭以及環境污染問題日漸突出.為了緩解能源匱乏以及應對生態環境污染的難題,可再生能源的開發與利用逐漸成為民眾關注的熱點問題.為了選擇最適合開發利用的可再生能源,有關部門邀請三位專家E1,E2,E3,從經濟效益X1,資源豐富度X2,技術水平X3,環境壓力X4,社會支持及國家政策X5等方面,對三個方案風能A1,水能A2,太陽能A3進行評估.第一維語言評價集為S={s0= 特差,s1= 很差,s2= 差,s3= 較差,s4= 中等,s5= 較好,s6=好,s7= 很好,s8= 特好}, 第二維語言評價集為C={c0= 很沒把握,c1= 沒把握,c2= 一般,c3=有把握,c4=很有把握}.三位專家對三種不同的待選方案做出的一維語言評價矩陣如表2～表4 所示.

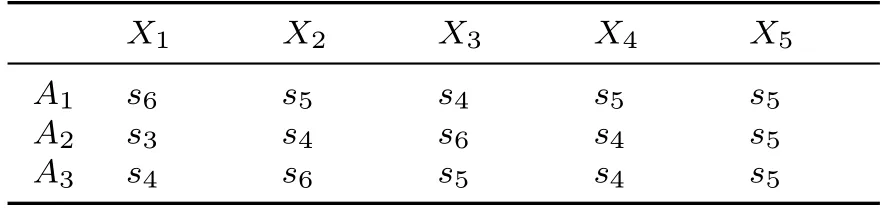
表2 專家E1給出的一維語言評估矩陣D1Table 2 One dimension assessment matrix D1 given by E1

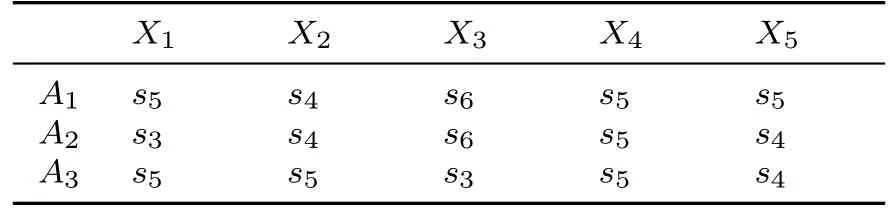
表3 專家E2 給出的一維語言評估矩陣D2Table 3 One dimension assessment matrix D2 given by E2

表4 專家E3 給出的一維語言評估矩陣D3Table 4 One dimension assessment matrix D3 given by E3

4.1 評價決策過程

步驟1專家給出的第一維語言評價值對于第二維語言評價集的隸屬度,如下表5～表13所示.

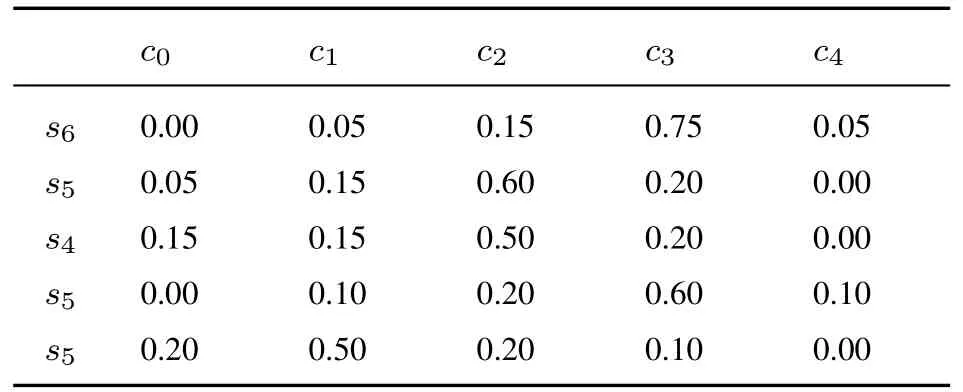
表5 專家E1 給出的關于方案A1 評價值的隸屬度Table 5 The membership degree of evaluation value of A1 by E1

表6 專家E1 給出的關于方案A2 評價值的隸屬度Table 6 The membership degree of evaluation of A2 by E1

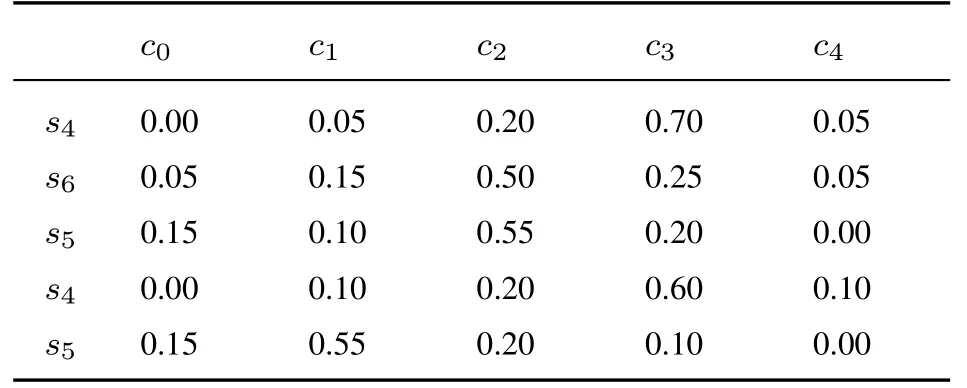
表7 專家E1 給出的關于方案A3 評價值的隸屬度Table 7 The membership degree of evaluation value of A3 by E1

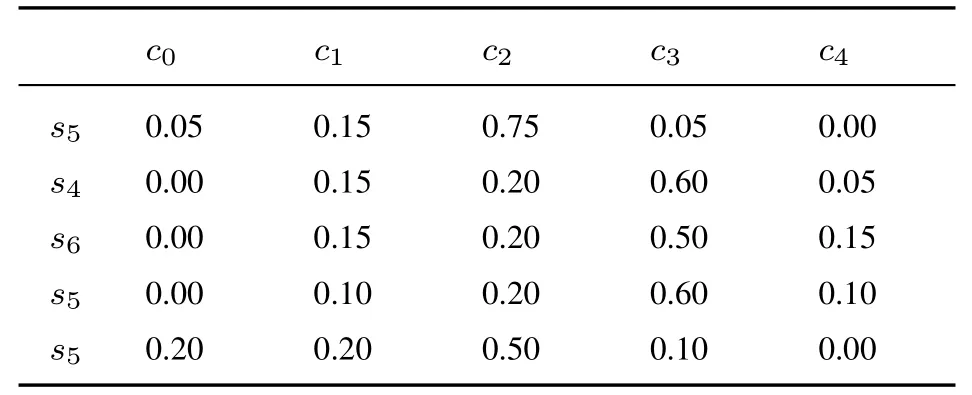
表8 專家E2 給出的關于方案A1 評價值的隸屬度Table 8 The membership degree of evaluation value of A1 by E2

表9 專家E2 給出的關于方案A2 評價值的隸屬度Table 9 The membership degree of evaluation value of A2 by E2

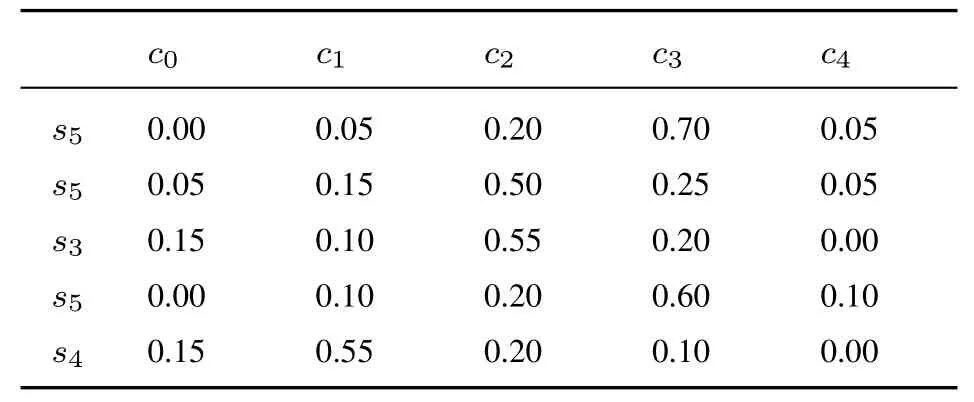
表10 專家E2 給出的關于方案A3 評價值的隸屬度Table 10 The membership degree of evaluation value of A3 by E2

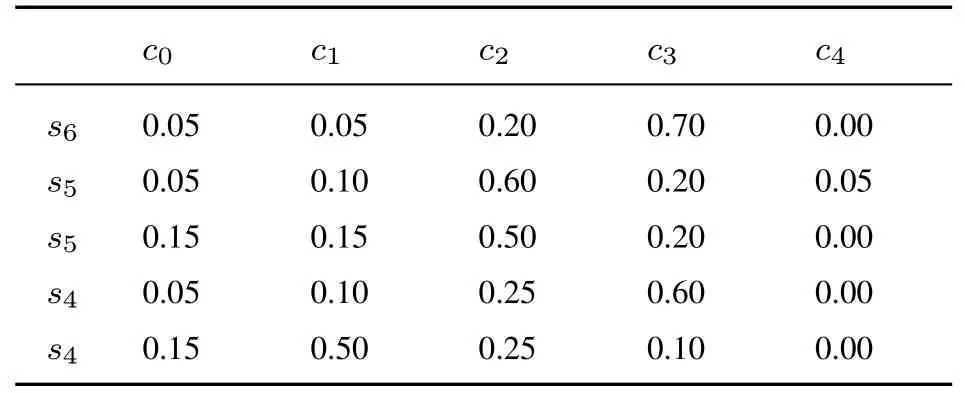
表11 專家E3 給出的關于方案A1 評價值的隸屬度Table 11 The membership degree of evaluation value of A1 by E3

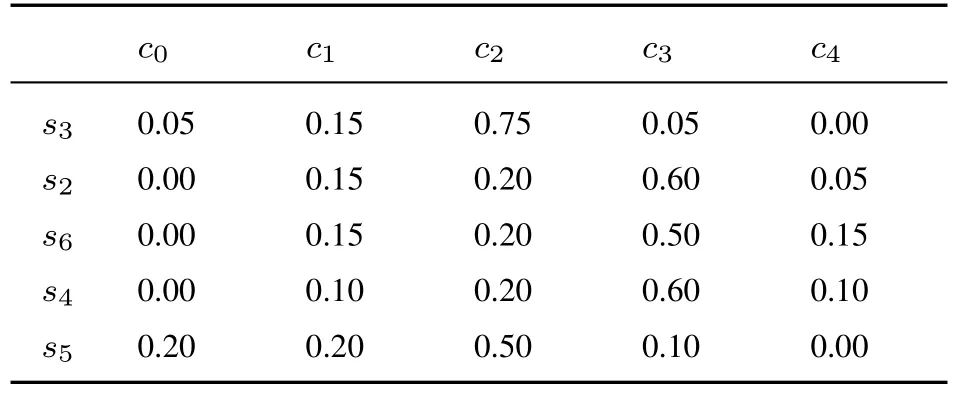
表12 專家E3 給出的關于方案A2 評價值的隸屬度Table 12 The membership degree of evaluation value of A2 by E3

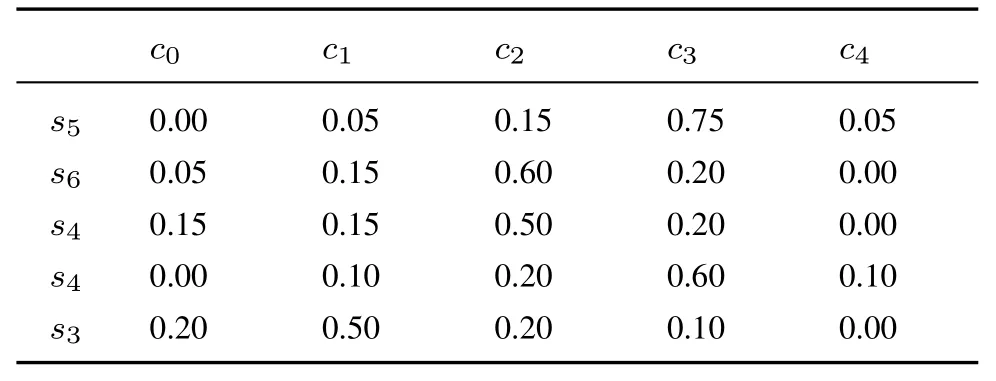
表13 專家E3 給出的關于方案A3 評價值的隸屬度Table 13 The membership degree of evaluation value of A3 by E3

由式(18)計算可得相應的可信性測度

由式(19)計算可得確信度函數

步驟2通過式(20)將一維語言評價值標準化為,進而根據式(13)將其轉化為二維二元語義,可得決策矩陣～如表14～表16 所示.

表14 專家E1 給出的二維二元語義評估矩陣Table 14 2-dimension 2-tuple linguistic information assessment matrix by E1

表14 專家E1 給出的二維二元語義評估矩陣Table 14 2-dimension 2-tuple linguistic information assessment matrix by E1

X1 X2 X3 X4 X5 A1 〈(s6,0),3.550〉 〈(s5,0),3.375〉 〈(s4,0),3.675〉 〈(s5,0),3.950〉 〈(s5,0),3.250〉A2 〈(s3,0),3.525〉 〈(s4,0),3.450〉 〈(s6,0),3.675〉 〈(s4,0),3.725〉 〈(s5,0),3.275〉A3 〈(s4,0),3.625〉 〈(s6,0),3.800〉 〈(s5,0),3.500〉 〈(s4,0),3.950〉 〈(s5,0),3.050〉

表15 專家E2 給出的二維二元語義評估矩陣Table 15 2-dimension 2-tuple linguistic information assessment matrix by E2

表15 專家E2 給出的二維二元語義評估矩陣Table 15 2-dimension 2-tuple linguistic information assessment matrix by E2

X1 X2 X3 X4 X5 A1 〈(s5,0),2.750〉 〈(s4,0),3.875〉 〈(s4,0),4.275〉 〈(s5,0),3.950〉 〈(s5,0),3.550〉A2 〈(s3,0),3.550〉 〈(s4,0),3.475〉 〈(s6,0),3.575〉 〈(s5,0),3.850〉 〈(s4,0),3.350〉A3 〈(s5,0),3.625〉 〈(s6,0),3.800〉 〈(s3,0),3.500〉 〈(s5,0),3.950〉 〈(s4,0),3.050〉

表16 專家E3 給出的二維二元語義評估矩陣Table 16 2-dimension 2-tuple linguistic information assessment matrix by E3

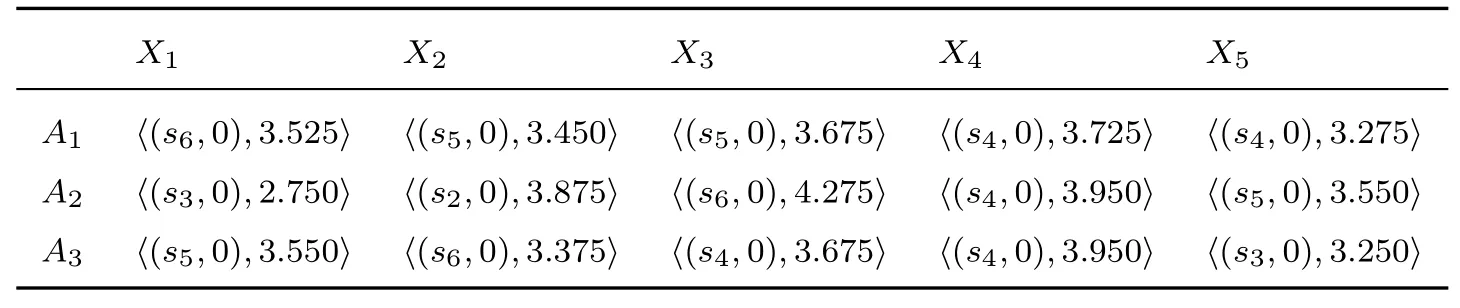
表16 專家E3 給出的二維二元語義評估矩陣Table 16 2-dimension 2-tuple linguistic information assessment matrix by E3

X1 X2 X3 X4 X5 A1 〈(s6,0),3.525〉 〈(s5,0),3.450〉 〈(s5,0),3.675〉 〈(s4,0),3.725〉 〈(s4,0),3.275〉A2 〈(s3,0),2.750〉 〈(s2,0),3.875〉 〈(s6,0),4.275〉 〈(s4,0),3.950〉 〈(s5,0),3.550〉A3 〈(s5,0),3.550〉 〈(s6,0),3.375〉 〈(s4,0),3.675〉 〈(s4,0),3.950〉 〈(s3,0),3.250〉

步驟3利用λh=計算可得決策者權重λ=(0.41,0.25,0.34).

步驟4由式(21)計算可得綜合決策矩陣為

步驟5采用AHP 法計算屬性的主觀權重,采用熵值法計算屬性的客觀權重,然后通過式(22)求解得到組合權重,計算結果及分析如表17 所示.

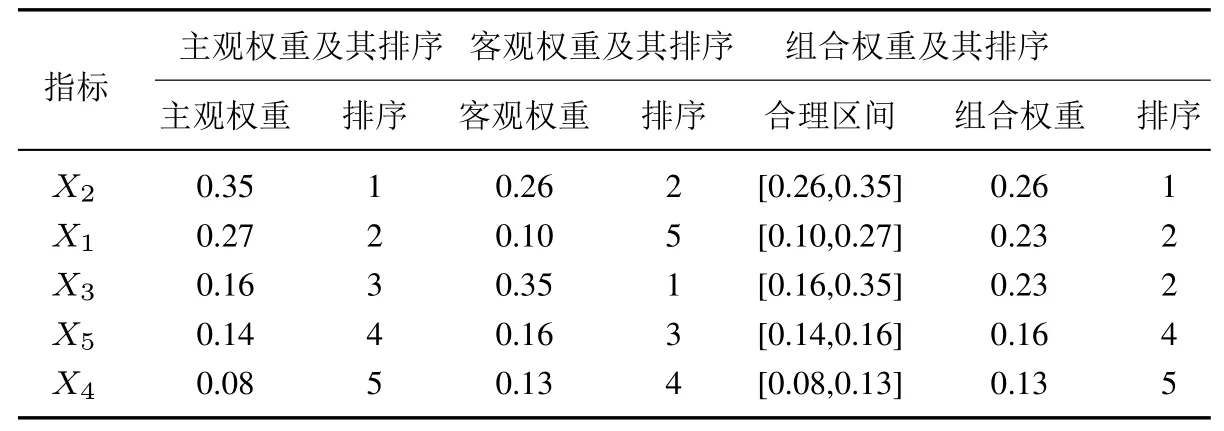
表17 主客觀權重及組合權重Table 17 Subjective and objective weights&combined weights

步驟6根據式(23)可得每個方案的二維二元語義最終值,結果如表18 所示.

表18 二維二元語義最終值Table 18 The final values of 2-dimension 2-tuple linguistic information

根據式(24)可得三個方案的期望值E[A1]=0.668 4,E[A2]=0.4150,E[A3]=0.586 2.

由此可知,三個方案的優劣排序為A1?A3?A2,故A1(風能)為最優方案.

4.2 方法比較分析

為了進一步驗證本文方法的優越性與合理性,采用文獻[20]中所提出的二維二元語義群決策方法,與本文評價結果進行比較分析.基于傳統的二維二元語義期望值函數和距離函數,根據本文所求得的權重信息,計算出各個方案的綜合評價值,如表19 所示.

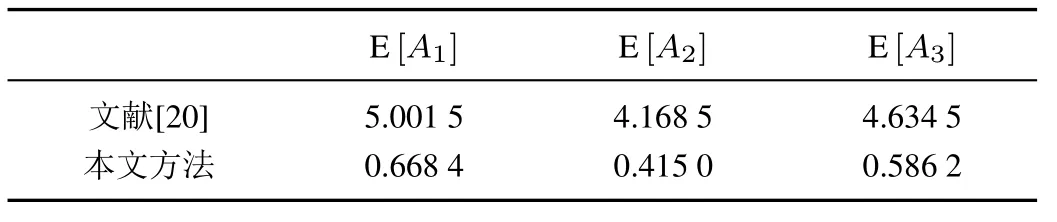
表19 不同方法評價結果對比Table 19 Comparison of evaluation results of different methods

由表19 可知, 基于文獻[20]的方法計算得到的三個方案優劣排序結果為A1?A3?A2, 方案A1(風能)為最優方案,與本文方法所得結果一致,說明本文所提方法是有效的.但是,三個方案綜合評價值的差值并不是很大,在進行方案選擇時會對決策者造成不必要的干擾.這是由于文獻[20]的決策方法所采用的二維二元語義期望值函數,其實質只是將一維、二維語言信息進行簡單相乘,并沒有考慮到第二維語言信息本身所存在的意義,據此改善模型所定義的二維二元語義在處理信息時就不夠準確;其次,其所采用的語言評估標度也存在不合理之處,這就會進一步造成信息處理時的不精確.因此,與傳統二維二元語義方法相比,本文方法在信息處理時更加精確,也更符合實際決策問題.

4.3 敏感性分析

屬性權重在多屬性群決策中起著至關重要的作用,由于屬性權重確定方法存在著優劣之分,采用不同的屬性權重計算方法就會得到不同的結果,這可能會對群決策結果造成一定的影響.因此,有必要對群決策結果進行敏感性分析.

針對上述算例,圖2 給出了敏感性分析的結果.

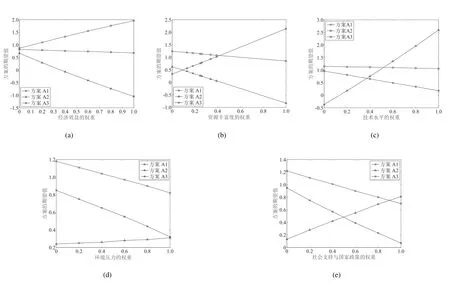
圖2 指標權重對方案期望值的影響Fig.2 The influence of index weight on the expected value of the scheme

當改變某一指標的權重時, 其余指標權重按比例變化, 如表17 所示.各指標初始權重分別為經濟效益0.225,資源豐富度0.26,技術水平0.225,環境壓力0.13,社會支持及國家政策0.16.當經濟效益的權重由0.225 變為0.5 時,其它指標權重之和為1?0.5=0.5.將該權重之和按比例分配給其它指標.例如,對于技術水平來說,wX3=0.5×0.225/(1?0.225)=0.145.

由圖2 可知, 環境壓力指標對選擇決策沒有敏感性, 無論其權重如何變化決策結果排序均為A1?A3?A2.經濟效益指標對其權重變化表現出輕微的敏感性,除非當其權重減少到0.18 左右,否則優劣排序一直為A1?A3?A2,決策結果幾乎不發生變化.與經濟效益指標相似,社會支持及國家政策對其權重變化也表現出輕微的敏感性,除非當其權重增加到0.9 左右,否則均可選擇A1作為最優方案.而技術水平指標和資源豐富度指標對其權重變化較為敏感,當技術水平指標權重增加到0.5 左右時,決策結果排序就變成A2?A1?A3;當資源豐富度指標權重增加到0.42 左右時,決策結果排序就變成了A3?A1?A2.這說明該問題中最敏感因素為技術水平指標和資源豐富度指標,即這兩個指標是該決策問題的最關鍵指標.

5 結束語

本文針對群決策過程中存在的決策信息模糊和信息處理不夠精確的問題,考慮到合理的語言標度更能符合專家的心理判斷,提出了一種基于正態分布的二元語義表示模型,使得決策者能夠給出更加合適、準確的評價信息.基于可信性測度的原理,給出了新的二維二元語義距離公式和期望值函數,進而解決信息在轉換處理過程中的不精確性.通過可再生能源選擇的算例分析驗證了該方法的可行性和科學有效性.敏感性分析表明,屬性權重的微小變化并不會導致決策結果的排序發生任何變化.這說明該方法具有較好的抗干擾能力,能夠準確地選出最優方案.