無砟軌道自密實混凝土早期溫度場及其影響研究

魏春城，楊榮山，張光明，常逢文，孫澤江

(西南交通大學高速鐵路線路工程教育部重點實驗室，成都 610031)

CRTSⅢ型板式無砟軌道的自密實混凝土層在灌注早期由于水化作用會導致自密實混凝土層內部溫度升高，在混凝土水化熱和氣象因素等共同作用下，軌道結構會產生整體溫降并形成內外不均勻的溫度分布，從而產生溫度應力，同時自密實混凝土灌注早期還會產生收縮應力。自密實混凝土的早期應力會對軌道結構產生不利影響，若早期養護不當，過大的早期應力會導致軌道板與自密實混凝土層間離縫、自密實混凝土裂紋等病害，影響無砟軌道結構的整體性和耐久性。

目前，國內外學者針對無砟軌道溫度場的研究方法可分為基于概率統計建立預估模型[1]以及基于傳熱學和氣象學的理論推導[2-4]。針對無砟軌道早期應力研究，蘇成光[5]建立了考慮混凝土水化熱及養生方式影響的雙塊式無砟軌道溫度場模型，計算了道床板零應力溫度；馬凱[6]建立板式無砟道岔三維瞬態溫度場及溫度應力模型，對底座板混凝土施工溫度和合理養護方式進行了討論；劉觀[7]通過有限元法分析研究了CRTSⅠ型雙塊式道床板混凝土溫度應力發展并探討了澆筑時機與拆模時間對應力的影響；韓超[8]建立了雙塊式無砟軌道早期溫度場模型，對道床板澆筑初期溫度應力進行計算，得出最大溫度應力出現在澆筑后11 h，且出現在軌枕與道床板的交界面處。目前，研究主要集中在CRTSⅠ型和CRTSⅡ型無砟軌道，但針對CRTSⅢ無砟軌道自密實混凝土層早期溫度及應力研究較少。

為研究自密實混凝土早期溫度的影響，開展自密實混凝土早期溫度場監測試驗，建立無砟軌道早期溫度場三維有限元模型，通過理論和試驗研究，分析自密實混凝土層早期應力并研究其變化規律和分布情況，研究結果對CRTSⅢ型板式無砟軌道結構設計和施工方法提供參考。

1 自密實混凝土早期溫度場試驗及理論計算

1.1 自密實混凝土早期溫度場試驗概況

為研究CRTSⅢ型板式無砟軌道自密實混凝土灌注早期溫度時空演化規律，課題組在四川省成都地區開展了自密實混凝土溫度監測試驗，試驗現場情況如圖1所示。試驗所用軌道板為預制軌道板，自密實混凝土在軌道板鋪設精調后采用現場灌注的方式施工，其長為5 600 mm，寬2 500 mm，高90 mm。在自密實混凝土層中部平面鋼筋網上布置PT100柱式鉑熱電阻溫度傳感器，其測量量程為-20～80 ℃，測量精度為±(0.15+0.002|t|)℃(|t|為實測溫度的絕對值)，具體布置方案如圖2所示。為排除現場施工機械的干擾，溫度監測開始于自密實混凝土灌注15h后，采集時間為2017年9月16日12時至2017年9月20日16時，采集頻率為1min/次。

圖1 自密實混凝土溫度監測試驗現場

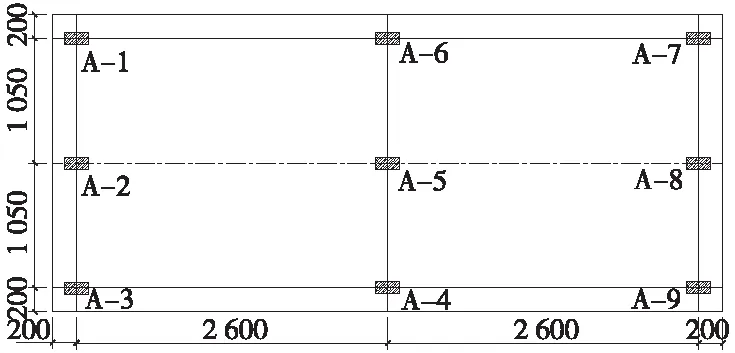
圖2 自密實混凝土溫度傳感器布置示意(單位：mm)

試驗期間氣溫、太陽輻射與日平均風速如圖3所示。由圖3可知，在該段時間內軌道板附近平均氣溫為25 ℃，最高氣溫約34 ℃；當地太陽輻射值較低，最高輻射僅為650 W/m2；試驗場地內風速較小，最高平均風速約1.7 m/s。

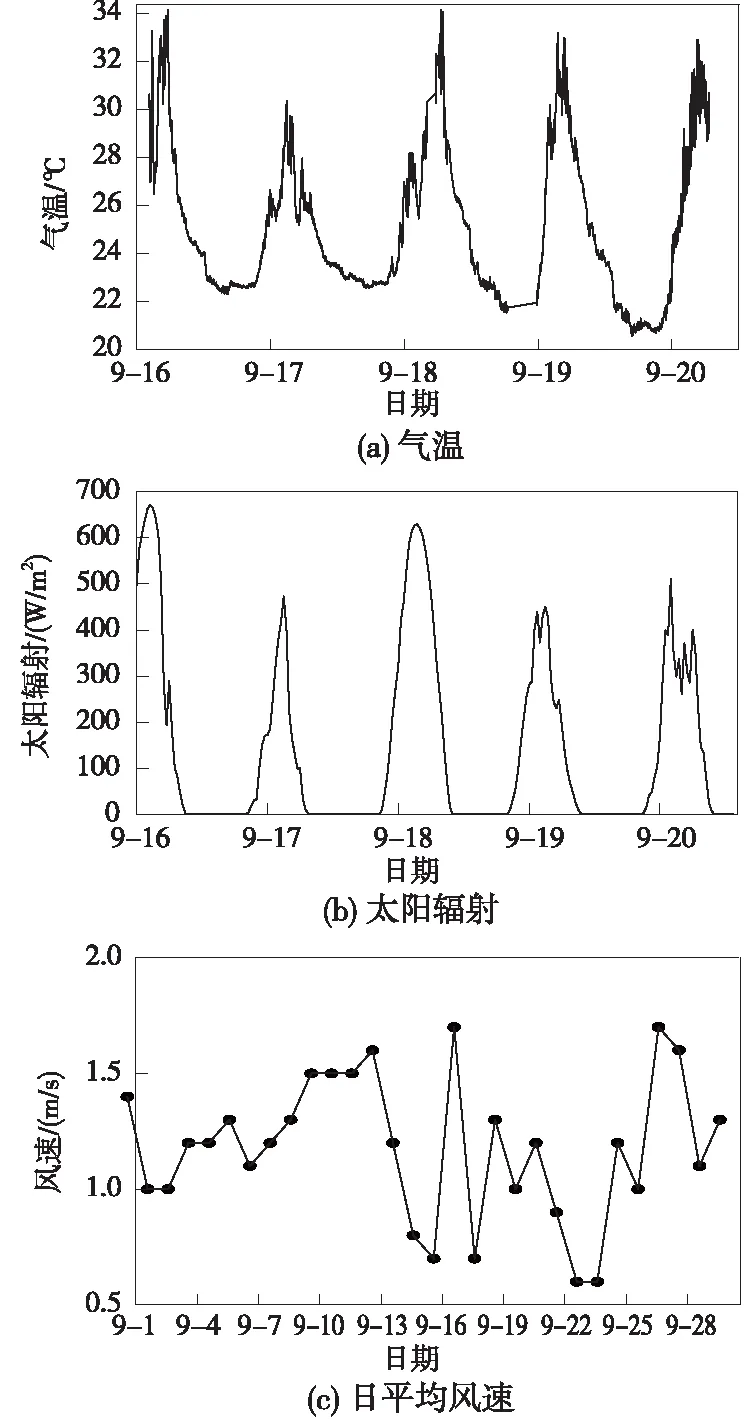
圖3 氣象數據

1.2 溫度場計算模型

CRTSⅢ型板式無砟軌道垂向結構依次為鋼軌、扣件、軌道板、自密實混凝土層、隔離層和底座板，基于有限元軟件建立CRTSⅢ型板式無砟軌道溫度場實體計算模型，如圖4所示。建模時忽略鋼軌和扣件的影響，該模型的主要參數見表1[9-10]。

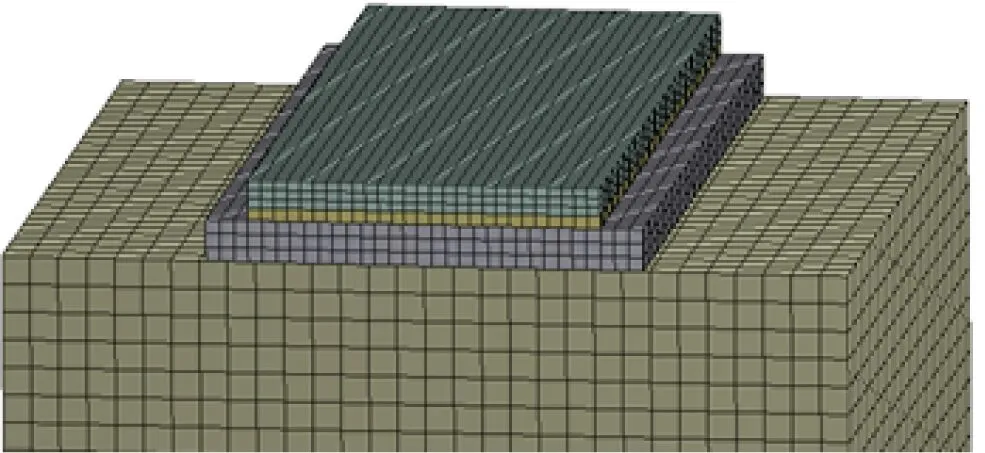
圖4 CRTSⅢ型板式無砟軌道溫度場計算模型

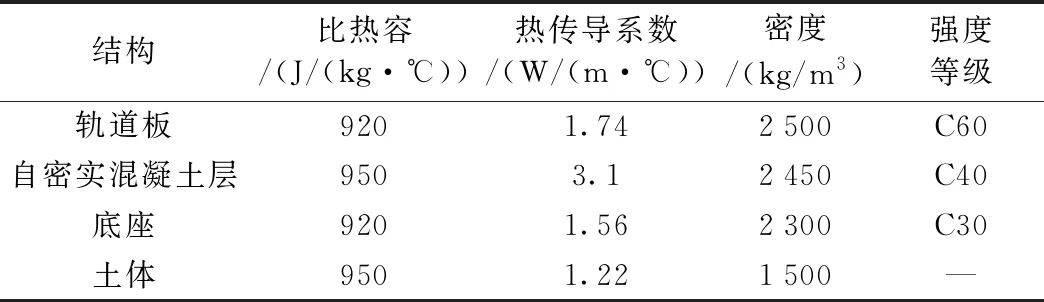
表1 計算參數

由傳熱學原理可知，自密實混凝土灌注早期溫度場計算應考慮無砟軌道結構與自然環境的熱交換以及自密實混凝土水化生熱。首先，對結構進行穩態分析以求解初始溫度，穩態分析邊界條件為軌道板上表面施加該時刻氣溫，土體向下延伸10 m處取為下表面，施加成都地區大地恒溫層溫度16.5 ℃[11]，然后進行瞬態分析，計算隨自密實混凝土齡期變化的溫度場。

1.3 溫度場計算邊界條件

(1)太陽輻射吸收系數

太陽輻射為軌道結構提供主要熱量，以太陽輻射吸收系數as表示軌道吸收太陽輻射的能力，由于軌道板處于自密實混凝土灌注早期，as取值為0.60[12]。

(2)對流換熱系數

根據牛頓冷卻定律，無砟軌道外表面溫度與大氣溫度產生溫差時，兩者可進行對流換熱。軌道對流換熱能力可通過對流換熱系數hc表征，hc可按式(1)計算[13]

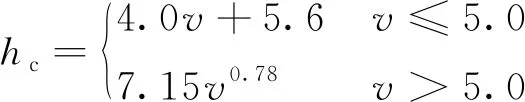
(1)

(3)輻射換熱

軌道結構在接收熱輻射的同時也向外界發射熱輻射，發射率定義為物體的輻射能力相對于同一溫度下黑體輻射能力的比值。據Stefan-Boltzmann[14]公式，用凈發射率ε和環境溫度計算大氣中有效熱輻射進入無砟軌道的熱流密度。

q1=εσ[(Tsky+273.15)4-(Ts+273.15)4]

(2)

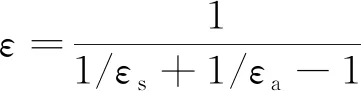
(3)

式中，q1為輻射熱流密度，W/m2；σ為Stefan-Boltzmann常量，取5.67×10-8W/(m·℃)；ε為凈發射率，按式(3)計算，其中，εs為軌道板表面發射率，取0.88，εa為大氣發射率，取0.8；Tsky為天空有效溫度，在南方夏季時取Tsky=Ta-14[15]，Ts為軌道板表面溫度。

(4)自密實混凝土水化熱

自密實混凝灌注早期水化反應放出大量的熱，可導致軌道結構內部溫度急劇升高。影響混凝土水化放熱的因素眾多，包括水泥品種、成分、灌注溫度等。混凝土水化熱可按下式計算[16]

Q(t)=Q0exp{-55[0.962exp(0.039T0)t]-1.25}

(4)

式中，t為時間，h；Q(t)為單位體積自密實混凝土水化熱總量，kJ/m3；Q0為單位體積自密實混凝土最終發熱量，kJ/m3，取110 885 kJ/m3[17]；T0為自密實混凝土灌注溫度，℃。

利用式(4)計算得到自密實混凝土水化熱曲線，如圖5所示。

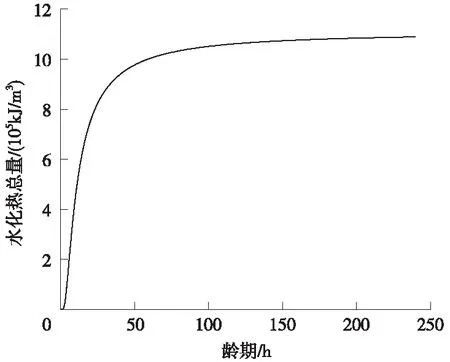
圖5 自密實混凝土水化熱曲線

1.4 自密實混凝土溫度時空演化規律分析

1.4.1 自密實混凝土溫度空間分布規律

應用前文模型，結合圖3氣象數據進行自密實混凝土層早期溫度場計算，測點平面溫度場計算結果如圖6所示。

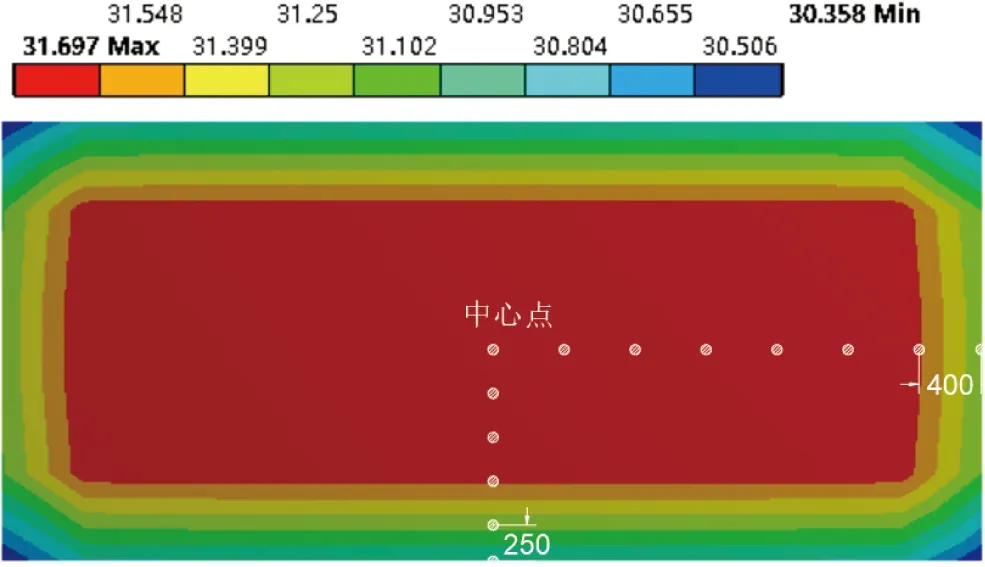
圖6 灌注后24h自密實混凝土溫度分布

根據圖6可知，灌注后24 h自密實混凝土層外部溫度較低，中心位置溫度較高，溫度呈環形分布。灌注后24 h的最高和最低溫度分別為31.70 ℃和30.36 ℃，溫差為1.34 ℃。

為進一步分析自密實混凝土溫度空間分布的規律，分別在自密實混凝土層中部平面內中心點所在橫、縱截面上，取距中心點不同距離的點，計算自密實混凝土灌注后24，72，115 h的溫度變化及相鄰點單位距離溫度差值，如圖7所示。

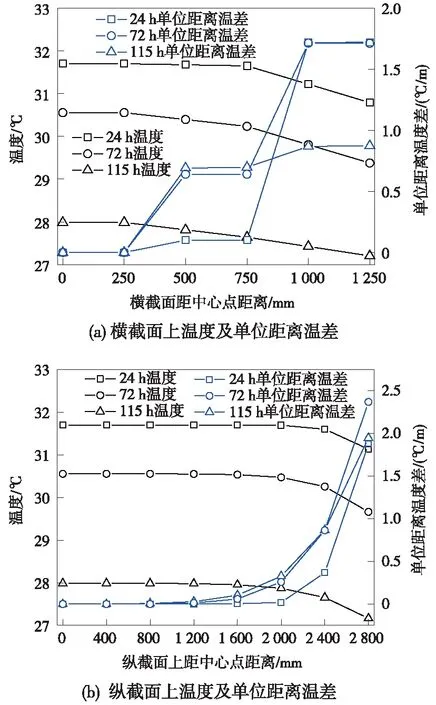
圖7 自密實混凝土中心點橫、縱截面溫度及單位距離溫差

由圖7可知，在自密實混凝土層中心點橫、縱斷面內，隨著距中心點位置的距離增加，溫度呈現非線性降低趨勢，而單位距離溫差則顯著增加。在中心點橫截面內，單位距離溫差最大值為1.72 ℃/m；在中心點縱斷面內，單位距離溫差最大值為2.37 ℃/m。說明距中心點位置距離越遠，溫度越低，溫度變化越明顯。

在中心點一定距離范圍內溫度與中心點溫度相差較小，單位距離溫差幾乎為0，此區域可定義為“高溫區”，隨著混凝土齡期的增長，“高溫區”范圍逐漸變小，在自密實混凝土灌注24～115 h，“高溫區”范圍從橫截面距中心點750 mm、縱截面距中心點2 000 mm減小為橫截面距中心點250 mm、縱截面距中心點1 200 mm。

1.4.2 自密實混凝土溫度時間演變規律

為更準確描述溫度場計算結果，將部分溫度測點的有限元計算結果與試驗測量結果進行對比，由于計算模型關于A-5中心對稱，故取A-4、A-5測點進行對比分析，如圖8所示。

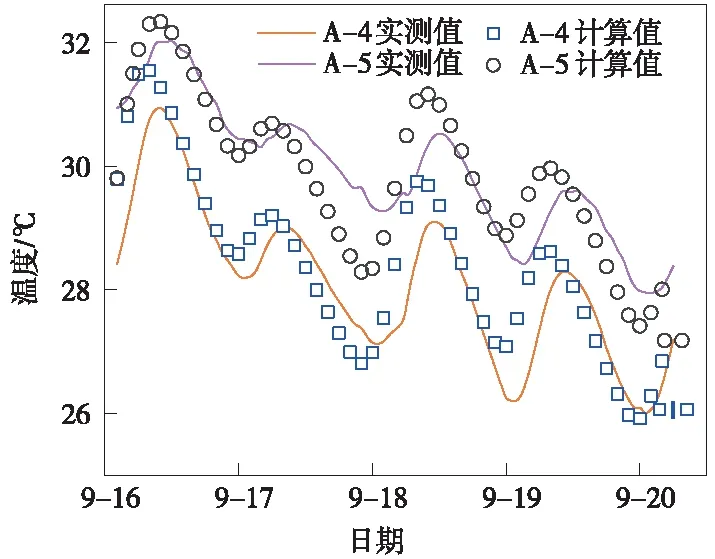
圖8 自密實混凝土各測點溫度計算值與實測值對比

由圖8可知，在自密實混凝土灌注溫度為25 ℃時，各測點數值模擬結果與實測值變化趨勢基本一致，計算結果與實際監測數據誤差較小，最大誤差為1.9 ℃，該溫度場模型合理，可用于自密實混凝土層早期應力計算。

經計算，自密實混凝土在灌注后22 h達到溫度極值，最高溫度為32.6 ℃，隨著時間的推移逐漸降低，灌注后115 h內最低溫度為24.4 ℃，溫度降低8.2 ℃，溫降幅度為25%。表明自密實混凝土在灌注后24 h內水化反應劇烈，生成大量的水化熱導致溫度迅速升高，隨后放熱程度逐漸減弱。整體溫度自密實混凝土受水化熱和外界熱交換影響呈波動式降低。

A-4和A-5測點在自密實混凝土灌注后115 h內最高溫度分別為31.6，32.4 ℃，溫度降低為5.7 ℃和5.0 ℃，溫降幅度分別為18%和15%。可知，降溫幅度由邊緣區域向中心區域逐漸降低。

2 自密實混凝土層早期應力計算

在自密實混凝土灌注早期，結構內部溫度場非線性分布會產生自生應力，由于自密實混凝土收縮受到約束會產生約束應力。當自密實混凝土積累的拉應力超過該齡期的抗拉強度，就會有開裂的風險，因此，自密實混凝土早齡期應力的研究對裂縫控制十分重要。

2.1 約束條件及參數設置

在應力計算中，將底座底端設置為全約束；軌道板和自密實混凝土采用綁定接觸，自密實混凝土和底座板之間由于隔離層的設置而采用摩擦接觸，摩擦系數取0.5[18]，自密實混凝土凸形擋臺和底座板凹槽起限制作用，設為綁定接觸。

自密實混凝土灌注早期彈性模量E(t)和抗拉強度ft(t)隨齡期增長，根據CEB-FIP 1990《歐洲混凝土規范》，自密實混凝土彈性模量和抗拉強度公式分別見式(5)、式(6)[6]，各結構其他力學參數見表2。

表2 力學參數

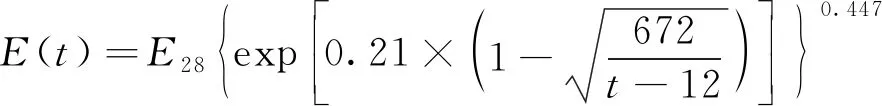
(5)

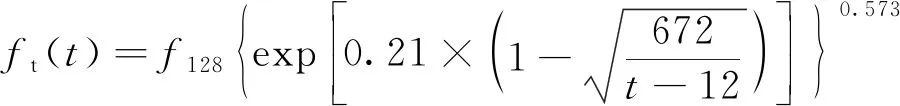
(6)

式中，E28為自密實混凝土28 d齡期的彈性模量，MPa；ft28為自密實混凝土28 d齡期的抗拉強度，MPa，取2.39 MPa；t為齡期，h。

2.2 自密實混凝土收縮應力

自密實混凝土早期的收縮包括干燥收縮和自生收縮。考慮兩者工程效應相似將其綜合計算。在計算中采用等效溫差的方法，其中，收縮應變隨齡期變化如式(7)[19]。

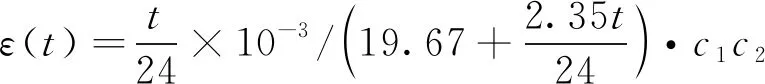
(7)

式中，t為齡期，h；c1為煤灰摻量影響系數，取0.973 46；c2為鋼筋線形約束影響系數，取0.825 76。

2.3 早期應力的徐變修正

早期混凝土的徐變特性會導致應力松弛，進而降低溫度和收縮產生的早期應力，故計算中需考慮徐變效應。計算考慮徐變后t時刻總應力計算如式(8)[20]

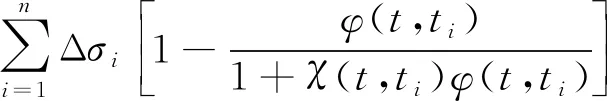
(8)

φ(t，t0)=φ1t0-d(t-t0)p

(9)

式中，φ(t，t0)為徐變系數，按式(9)計算，其中，φ1、d、p與材料有關，取φ1=0.9，d=0.32，p=0.32，該公式只適用于參考溫度為20 ℃的恒溫條件，計算時要將t、t0轉化為等效齡期；χ(t，t0)為老化系數，取χ(t，t0)=1。

在計算過程中，自密實混凝土應力發展時刻定義在“第一零應力溫度”T1時刻。所謂T1是指，混凝土終凝時，混凝土應力和強度開始發展時混凝土的溫度。可取自密實混凝土灌注600 min內最高溫度作為T1，并以此溫度作為參考溫度[5]。

2.4 早期應力計算結果2.4.1 徐變對早期應力的影響對比分析

利用自密實混凝土早期溫度場計算結果，輸入力學參數，對自密實混凝土進行熱應力耦合分析，分別計算自密實混凝土層灌注后115 h內考慮徐變和不考慮徐變時的部分測點應力，計算結果如圖9所示。

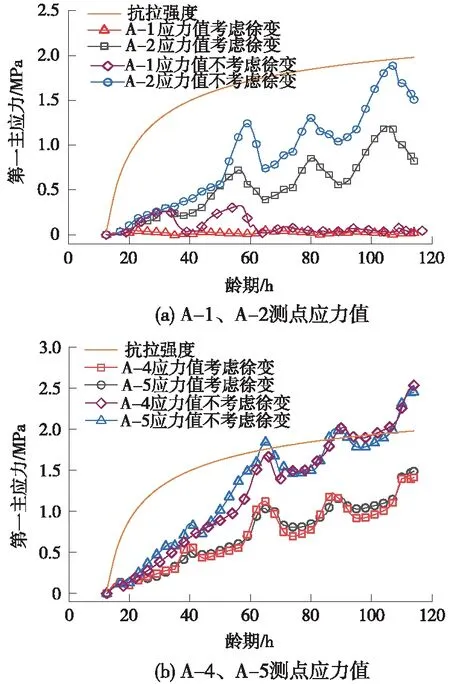
圖9 自密實混凝土第一主應力值考慮與不考慮徐變對比

由圖9可知，徐變可顯著降低自密實混凝土早期應力，在自密實混凝土灌注后115 h內，不考慮徐變情況下A-1、A-2、A-4、A-5測點最大應力值為0.03，1.88，2.45，2.53 MPa，其中，A-4、A-5處應力值已超過抗拉強度，A-2測點也有很大風險超過抗拉強度；而此時考慮徐變A-1、A-2、A-4、A-5測點最大應力值僅為0.008，1.2，1.49，1.41 MPa，低于抗拉強度。可見除A-1外，其余各點考慮與不考慮徐變后應力均有較大變化，考慮徐變后早期應力降低最大約45%。

2.4.2 自密實混凝土早期應力變化曲線

考慮徐變修正后，自密實混凝土灌注后115 h內4個測點第一主應力值變化曲線如圖10所示。

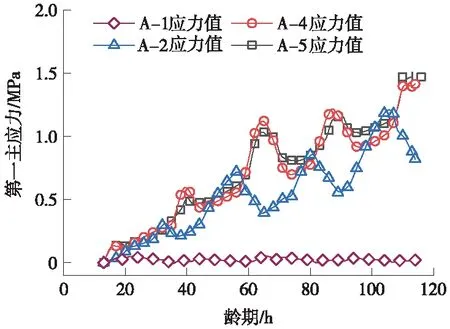
圖10 自密實混凝土第一主應力變化曲線

由圖10可知，A-2、A-4、A-5處第一主應力隨齡期均呈現出明顯的波動式增長趨勢。而A-1測點的應力值無明顯變化。其中，A-2測點應力值由0.14 MPa增長至0.82 MPa；A-4測點應力值由0.17 MPa增長至1.41 MPa；A-5測點應力值由0.17 MPa增長至1.48 MPa。說明在自密實混凝土灌注早期，由于彈性模量隨齡期增長、自密實混凝土收縮和內高外低的不均勻溫度場，在自身相互約束及外部約束條件下，自密實混凝土層第一主應力主要呈現隨齡期增長，而邊角處由于收縮應力和溫度應力均很小，其早期應力值無明顯變化。

自密實混凝土開裂風險較大位置為中心位置A-5、縱向中點邊緣位置A-4和限位凹槽附近A-2，但各處應力增長的主要原因不同。由于自密實混凝土水化放熱導致中心區域溫度高于邊緣溫度，在邊緣處混凝土的溫度收縮變形受內部約束，導致A-4測點的溫度應力值高于A-5測點，其最大差值為0.3 MPa，同時水化反應會導致自密實混凝土內部自生收縮量大于邊緣區域，造成A-5測點收縮應力高于A-4測點，其最大差值為0.16 MPa，而由于自密實混凝土的收縮在限位凹槽處受到約束，在限位凹槽處會產生較大的應力值。計算各測點灌注后24，72，115 h第一主應力值如表3所示。

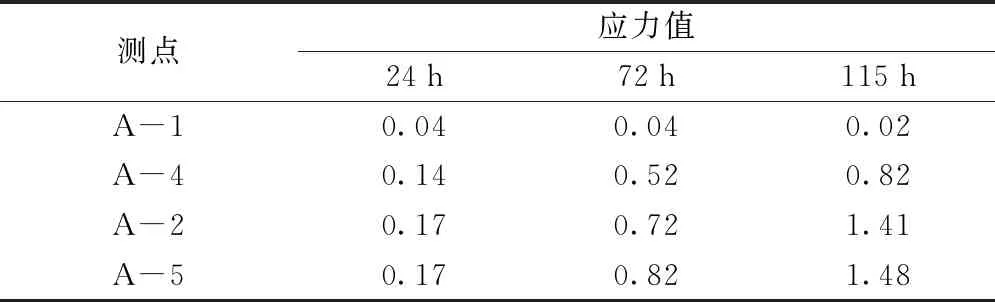
表3 部分測點應力值 MPa

3 結論

通過開展CRTSⅢ型板式無砟軌道自密實混凝土早期溫度場現場監測試驗，并建立自密實混凝土早期溫度場計算模型，分析了自密實混凝土早期溫度時空演變規律，最后計算了考慮收縮和徐變影響的自密實混凝土早期應力，分析應力值變化和分布規律，研究徐變對早期應力的影響，得出以下結論。

(1)建立的早期溫度場模型計算結果與試驗監測數據吻合較好，計算模型基本合理，可為通過氣象數據進行自密實混凝土早期溫度場及早期應力的計算提供參考依據。

(2)自密實混凝土灌注后呈現外部溫度低，中間溫度高的環形溫度分布，與中心位置距離越遠，溫度越低，溫度變化越明顯，在中心位置一定范圍內存在一個溫度較高，單位距離溫差很小的“高溫區”，且該區域隨齡期增長逐漸變小。在25 ℃灌注溫度條件下，自密實混凝土灌注后24 h內達到最高溫度32.6 ℃，灌注后115 h內溫度降低8.2 ℃，溫降幅度達25%。

(3)自密實混凝土徐變作用可導致早期應力最大降低約45%，自密實混凝土早期應力隨齡期呈波動式增長，本試驗情況下灌注后115 h內最大應力值增長至1.48 MPa，接近該齡期自密實混凝土抗拉強度1.98 MPa，自密實混凝土中心區域、縱向中點邊緣區域和限位凹槽附近存在較大開裂風險。