混合效應模型的雙MCP懲罰分位回歸研究

周 霖，羅幼喜

(湖北工業大學理學院，武漢 430068)

隨著數據收集和存儲能力的不斷進步，數據獲取的方式和途徑越來越多，數據之間的關系也越來越復雜.如何針對高維復雜數據進行統計建模分析是一個亟待解決的問題.原始的變量選擇方法由于其方法本身的局限性，在面對高維復雜數據時顯得力不從心.近些年，隨著對變量施加正則化懲罰理論的提出，不同的懲罰方法被運用到變量選擇的領域內.Ridge回歸采用L2正則化懲罰，通過嶺跡的圖像來判斷冗余變量，從而降低變量之間共線性的影響.Tibshurani[1]提出了LASSO (least absolute shrinkage and selection operation)回歸，采用L1正則化懲罰，在估計回歸系數時自動對變量進行選擇，將冗余變量的系數壓縮為0.LASSO懲罰函數為凸函數，且是有偏估計，通過減小預測模型的方差達到降低預測總誤差的目的，但容易存在過度壓縮系數的缺點.為了進一步降低預測總誤差，Fan和Li[2]提出了SCAD懲罰，它不僅對于很小的回歸系數壓縮到0，而且是一種近似無偏估計.Zhang[3]提出的MCP懲罰(minimax concave penalty)，采用對回歸系數有差別的懲罰，在保留SCAD懲罰優點的同時得到更加精確的估計.基于此，越來越多的學者將MCP懲罰運用在各個領域研究中，在此基礎上進行優化，并在圖像去噪[4]和圖像重建[5]中有了較大的進展.

在混合效應模型中，考慮到樣本的數據有一定的關聯性，在模型中添加了隨機效應項.如果僅考慮固定效應而忽視隨機效應的影響，則會給最后的估計帶來偏差，但是無關的隨機效應太多則會導致求解過程中隨機效應的協方差陣不可逆，不利于估計，因此如何解決個體的隨機效應所帶來的誤差是高維混合效應模型進行變量選擇的關鍵.

將混合效應模型和分位回歸聯合起來，在不同的分位點進行變量選擇是一個新興的研究領域.現有的文獻中，多數學者都是對隨機效應進行L1正則化[6-8]，該方法只能剔除冗余的隨機效應，減少隨機效應的數量，但是無法選擇出固定效應中的重要預測變量.羅幼喜[9]針對此問題提出來一種雙Lasso正則化分位回歸法(DLQR)，對模型中的固定效應和隨機效應同時施加L1懲罰，使得模型的冗余度大大降低.但是L1正則化得到的結果為有偏估計，本文以MCP正則化替代L1正則化，提出雙MCP正則化分位回歸法(DMQR).

1 模型與方法

傳統的線性混合效應模型為：

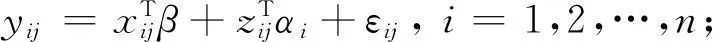
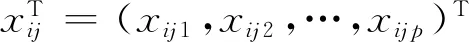
在實際生活中，數據往往存在異方差或者尖峰、后尾等情況，使得傳統的均值回歸效果不好，且一條回歸線所反映的信息也是有限的，分位回歸相對于均值回歸，其應用條件更加寬松，依據不同的分位數，對自變量進行回歸，能更好的描述自變量對因變量的變化范圍以及條件分布形狀的影響.Koenker和Bassett[10]提出線性分位回歸：

Q(τ)=inf(y：F(y)≥τ)，

其中，inf表示最大下界，Koenker[6]考慮了含隨機截距的條件分位回歸模型：

i=1，2，…，n，

(1)

并提出對個體波動施加L1正則化壓縮的分位回歸方法，數學表達式如下：

(2)

在實際問題中，有時個體效應不僅對模型截距有影響，也可能對模型的斜率有影響，將上述回歸模型推廣到既包含隨機截距又包含隨機斜率的條件分位回歸模型，即在給定個體隨機效應αi條件下，響應變量的τ分位回歸函數為：

j=1，2，…，ni；i=1，2，…，n，

(3)

羅幼喜[9]提出了DLQR方法，對個體效應施加L1懲罰以防止模型的過擬合，同時對固定效應施加L1懲罰來剔除冗余變量，選出重要的自變量，減少模型的冗余度，即極小化下式：

(4)

其中，λα為對個體效應施加的懲罰參數，λβ為對固定效應施加的懲罰參數.ρτ(·)為分位回歸函數，其表達式如下：

Lasso懲罰函數為凸函數，且是有偏估計，通過減小預測模型的方差達到降低預測總誤差的目的，但容易存在過度壓縮系數的缺點.為了進一步降低預測總誤差所提出的SCAD懲罰，它不僅對于很小的回歸系數壓縮到0，而且是一種近似無偏估計.之后提出的MCP懲罰，采用對回歸系數有差別的懲罰，在保留SCAD懲罰優點的同時得到更加精確的估計.MCP懲罰函數的數學表達式如下：

(5)

上式中，λ為正則參數，用來調整懲罰力度；a為調整參數，用來控制懲罰范圍.其懲罰力度為：

(6)

當|β|≤aλ時，MCP的懲罰力度會隨著參數絕對值的增大而減小，當|β|=0時其懲罰力度最大為λ，當|βi|=aλ時，其懲罰力度變為0，當回歸系數繼續增大時其懲罰力度保持為0不變.將Lasso與MCP懲罰的懲罰力度可視化如下圖1所示.

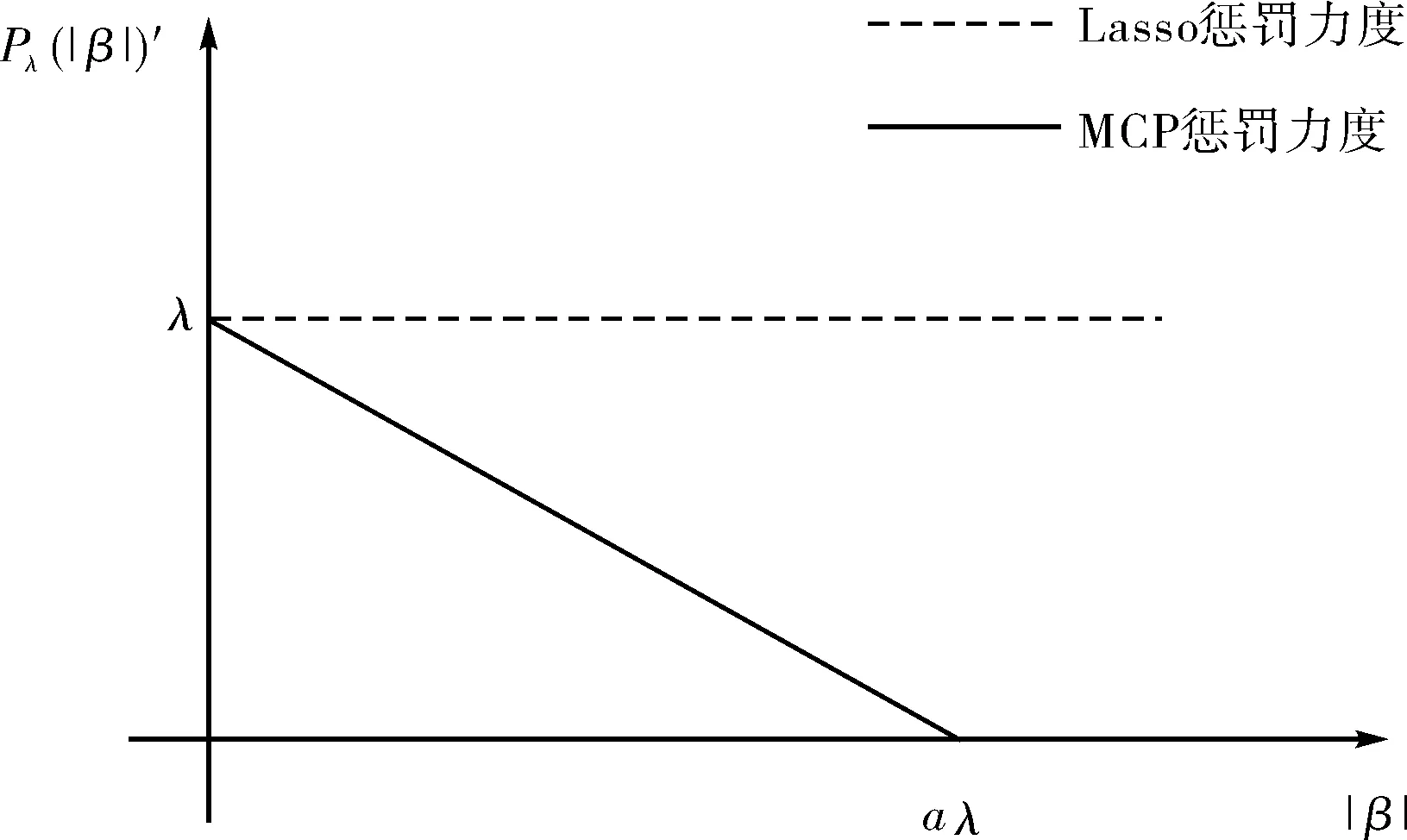
圖1 Lasso與MCP懲罰力度圖Fig.1 Lasso and MCP penalty intensity diagram

從上圖可以看出，Lasso對回歸系數采用恒定的懲罰力度，而MCP對回歸系數采取有差別的懲罰，當|βi|≥aλ，其懲罰力度為0，其參數的估計類似于最小二乘估計，其擬合的系數結果更精確.基于此，本文將DLQR法中L1懲罰替換為MCP懲罰，提出了雙MCP正則化的分位回歸方法(DMQR)，即極小化下式：

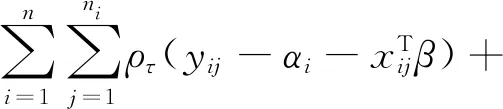
(7)

其中，Pλβ(|βl|)表示對固定效應施加MCP懲罰，Pλα(|αit|)表示對個體效應施加MCP懲罰.

2 回歸系數估計方法與正則化參數的選取準則

2.1 回歸系數估計方法

針對高維非凸懲罰的分位回歸問題，Wang和Peng[11]提出了迭代坐標下降(QICD).QICD算法將MM算法與坐標下降算法相結合.具體地說，首先用一個優化函數來替代非凸懲罰函數，并得到新的目標函數.然后，將關于目標參數的每次和每次循環替代所有參數，直到收斂為止.對于每個坐標下降步驟，只需要計算單變量加權中位數，可確保快速計算.具體計算流程圖見表1．雙MCP正則化分位回歸估計可以采用交替迭代算法求解，即每次只求解單個MCP正則化分位回歸，具體迭代算法求解見表2.

表1 QICD 算法偽碼表Tab.1 QICD algorithm pseudo code table

表2 雙MCP懲罰分位回歸迭代算法Tab.2 Double MCP penalty quantile regression iterative algorithm

2.2 正則化參數選取準則

選擇合適的正則化參數對于MCP懲罰的效果很關鍵.在DMQR法中一共有4個正則化參數，即Pλβ(|βl|)中的aβ和λβ，Pλα(|αit|)中的aα和λα，為簡化計算量和降低模型的復雜度，一般建議aα=aβ=3.0[12].此時需要選擇的正則化參數只有兩個，即調整固定效應的懲罰力度的λβ和調整個體效應懲罰力度的λα.運用上述迭代算法，每次迭代過程中，只用考慮單個正則化參數，使得參數選取的復雜度大大降低.

Wang[13]在Fan和Li[14]的基礎上提出了具有一致性的BIC法用于正則化參數選取.其數學表達式為：

(8)

(9)

其中，

(10)

3 計算機模擬比較研究

3.1 稀疏模型下兩種懲罰方法的比較

數據生成的公式如下：

(11)

表3給出了τ=0.25，0.5，0.75三個不同分位點下的模擬結果，重復模擬次數為100次，衡量模型精度的均方誤差(MSE)定義如下：

(12)

C1=重要預測變量被正確選擇個數/真實重要預測變量總個數，

C2=冗余預測變量被正確排除個數/真實冗余預測變量總個數.

C1和C2取值介于0和1之間，C1越接近1 表示其挑選重要預測變量的能力越強，反之越差；C2越接近1表示其排除冗余預測變量的能力越強，反之越差.表3 還給出了100次重復模擬中3 個重要預測變量X1、X2、X5被正確選擇和5 個冗余預測變量X3、X4、X6、X7、X8被正確排除的總次數.其中，判斷是否選擇了某變量是根據對該變量系數估計是否為0 得到的(本次模擬基于R 3.6.2，platform為x86＿64-w64-mingw32條件下實驗運行).

表3 不同條件下兩種懲罰分位回歸結果Tab.3 Regression results of two penalty quantiles under different conditions

從變量選擇的角度分析，在不同的σ取值下，DLQR和DMQR都能準確的選擇出模型中的重要預測變量，但是在排除冗余變量方面，DLQR最多只能準確排除75%左右的冗余變量，而DMQR則能正確排除90%以上的冗余變量，使模型中的干擾變量更少，具體效果見圖2.

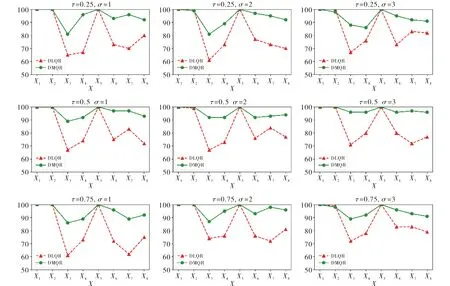
圖2 變量選擇效果Fig.2 Variable selection effect

從估計的精度來看，在τ=0.5；σ=1時，DMQR的估計精度最優.且在不同分位點，不同的σ取值時均比同等情況下的DLQR估計精度要高，且方差更小，具體效果見圖3.

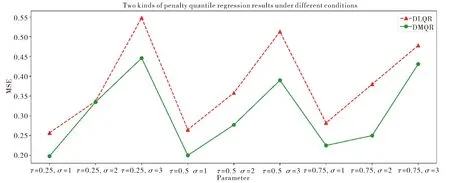
圖3 兩種懲罰精度對比圖Fig.3 Comparison of two types of penalty accuracy

保存每次DMQR法模擬產生的30個6維行向量αi(i=0，1，2，3，4，5)，得到一個30×6的α矩陣，即為隨機效應α的估計值，計算每一列的均值和方差作為隨機效應參數的一個估計.在不同分位點和不同信噪比下取100次模擬的平均值作為最后隨機效應α均值和方差的估計值，具體數據如下表4(上方數據為均值，括號內的數字為方差).

表4 隨機效應估計表Tab.4 Random effect estimate table

從均值的角度分析，在不同的分位點和不同的信噪比下，隨機效應系數α的均值都接近于0，擬合效果較好；從方差的角度分析，在不同分位點和不同信噪比下，α4，α5方差的擬合效果都很好，方差也接近于0，其他隨機效應系數的方差，隨著信噪比σ的增大，模擬效果逐漸降低，在不同分位點，當σ=1時其模擬效果最好，最接近于1，且在τ=0.5；σ=1，模擬效果最佳.

τ=0.5時，在不同信噪比下，保存每次模擬最后一步懲罰參數λα，λβ的值，100次模擬下，懲罰參數的箱線圖如圖4所示.

圖4 懲罰參數選取箱線圖Fig.4 Penalty parameter selection box plot

從上圖可以看出，隨機效應的懲罰參數λα其分布較為密集，其上四分位點與下四分位點包含的區間更小，且懲罰參數基本集中在0.09左右，固定效應的懲罰參數λβ其上四分位點和下四分位點所包含的區間更大，且其最大值與最小值之間的差距相較于λα更大.

3.2 不同誤差分布時估計的比較

下文在不同誤差分布情形下比較DMQR同其他幾種分位回歸方法在變量選擇和估計精度上的表現，數據生成的模型為式(11)，自變量系數設置為稠密、稀疏、高度稀疏三種不同情況：

1)稠密模型：β=(0.85，0.85，0.85，0.85，0.85，0.85，0.85，0.85)；

2)稀疏模型：β=(3，1.5，0，0，2，0，0，0)；

3)高度稀疏模型：β=(5，0，0，0，0，0，0，0).

取σ=1，τ=0.5，D=diag(2，2，2，2，0，0)，取誤差εij分別來自N(0，1)，t(3)及Cauchy(0，1)分布.比較的方法有：①普通分位回歸(QR)；②雙Lasso懲罰分位回歸(DLQR)；③雙MCP懲罰分位回歸(DMQR).表4、表5、表6給出了各種情況下重復100次的模擬結果.

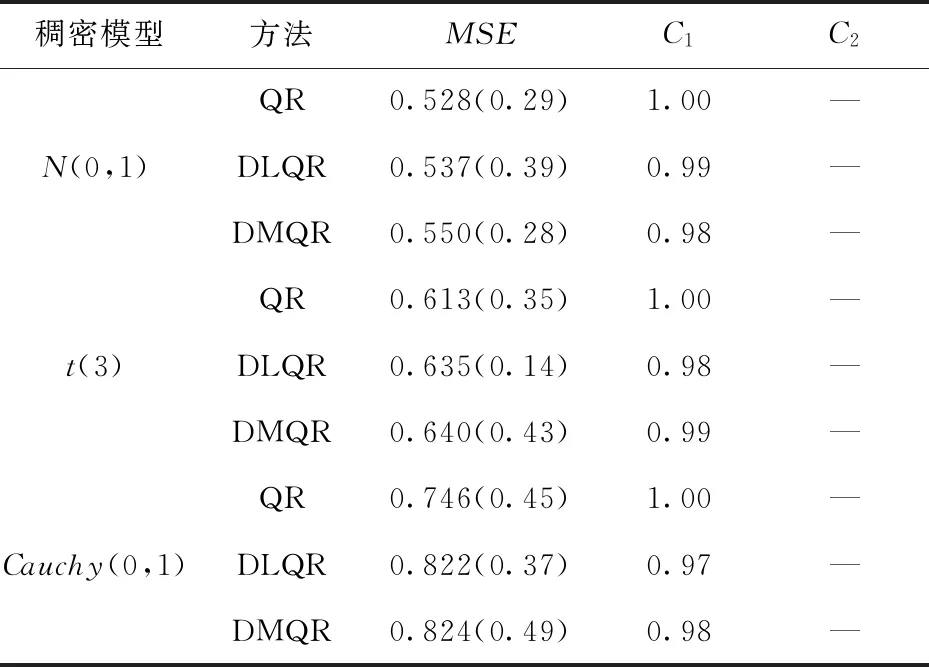
表5 稠密模型下模擬結果Tab.5 Simulation results under dense model

表6 稀疏模型下模擬結果Tab.6 Simulation results under sparse model

在稠密模型下，所有的變量均為重要預測變量，所以不存在正確排除冗余變量，故C2不存在.從MSE角度來看，不論誤差服從何種分布對系數進行懲罰后的模型在精度上面不如直接進行分位回歸的模型，DMQR模型和DLQR模型的擬合精度相差不大，主要原因是在稠密模型下，所有變量都不需要進行懲罰，故直接分位回歸(QR)得到的結果是最好的.

從誤差服從的不同分布來看，當誤差服從正態分布時，三種估計方法的精度最高，當誤差服從柯西分布時，估計的誤差最大，且對系數進行懲罰后，C1的值不能完全達到1.

在稀疏模型下，普通的分位回歸(QR)在排除模型中冗余變量的能力為0，因為普通分位回歸不能對變量進行選擇，只能將所有的變量均視為重要變量保留在模型中.而對系數施加懲罰后的方法則能排除模型中的冗余變量，但是不同懲罰所得到的結果也不同.

從排除模型中冗余變量的能力來看，DMQR剔除冗余變量的效果最好，能剔除90%以上的冗余變量，且在誤差服從標準正態分布時的效果最好，達到了94%.而DLQR只能剔除約70%以上冗余變量，從估計的精度來看，DMQR在3種方法中的估計精度最高，且在誤差為正態分布時的精度最高，當誤差為柯西分布時的精度最低，具體效果如圖5.

圖5 稀疏模型下擬合估計效果圖Fig.5 Fitting estimation effect diagram under sparse model

在高度稀疏模型下，無論誤差服從什么分布，DLQR法能剔除約80%以上的冗余變量，DMQR法能剔除約90%的冗余變量，雖然DMQR法的效果仍比DLQR法的結果好，但兩者在剔除冗余變量上的差距相較于稠密模型和稀疏模型縮小了許多.在模型的精度上面，DMQR法要優于DLQR法，DMQR法在正態分布時精度最高，誤差為0.188，說明DLQR法雖然在高度稀疏模型下能夠很好的排除冗余變量，但是對重要變量的擬合精度不高，擬合出來的結果與真實結果差距較大，擬合效果如圖6.

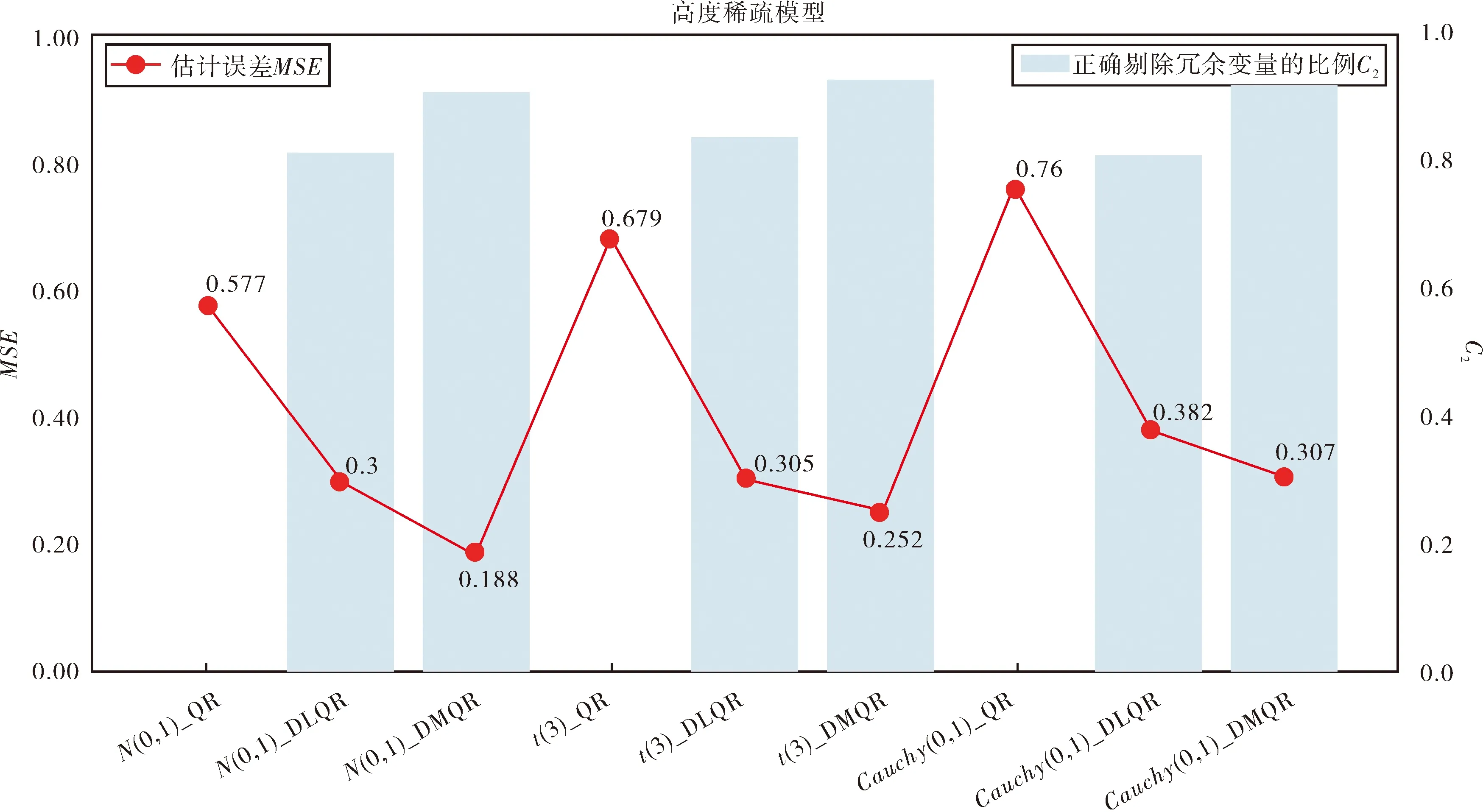
圖6 高度稀疏模型下擬合效果圖Fig.6 Fitting effect diagram under highly sparse model

3.3 高維情況比較

本節在高維情形下考察雙正則化分位回歸DLQR和DMQR的表現.數據的生成模型仍為式(7)，但減少樣本量至n=10，m=10，即總樣本量為100.在模擬(2)的稀疏模型中額外添加102個獨立噪聲變量X9，X10，…，X110，所有變量均獨立同分布于N(0，0.52)，在添加噪聲變量后，總的變量個數為110個，大于總樣本量.其中重要的預測變量為3個，冗余變量為107個.另外設σ=0.5 ，D=diag(1，1，1，1，0，0).表7給出了兩種方法在τ=0.5 、0.9 兩個分位點下進行100次模擬估計的結果.

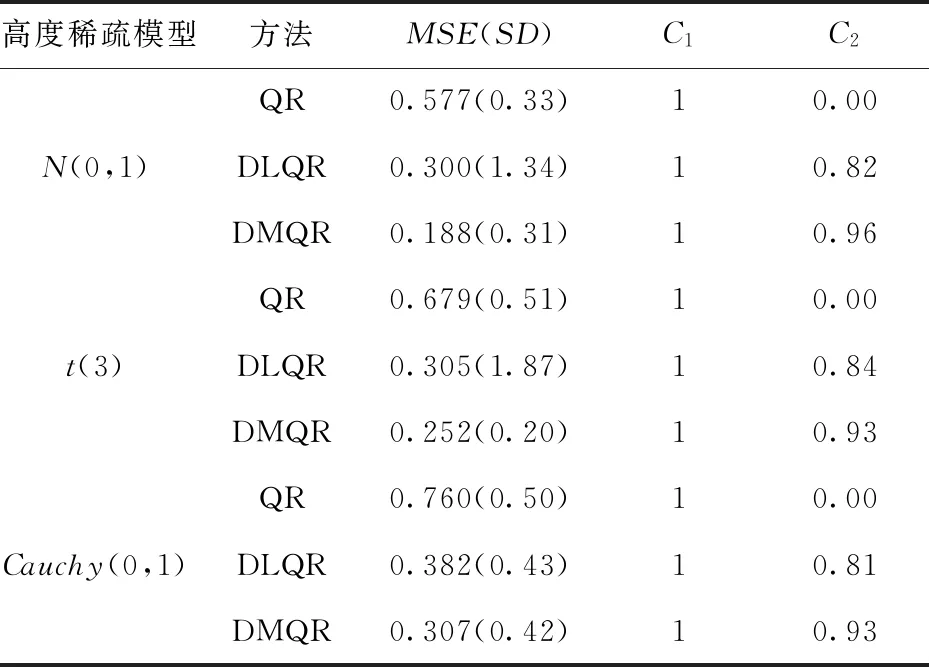
表7 高度稀疏模型下模擬結果Tab.7 Simulation results under highly sparse model

在高維情況下，DLQR法與DMQR法兩者的模擬差距非常明顯.從變量選擇的角度看，DLQR法只能正確剔除約81%的冗余變量，而DMQR法幾乎能剔除冗余變量的能力約為90%，且在τ=0.5 時能達到93%.在估計的精度上面，DMQR則要遠遠好于DLQR，DLQR法在不同分位點的平均誤差為5.94，而DMQR法的平均誤差僅為2.82.兩種方法在τ=0.5 時估計的精度均優于τ=0.9時的精度.

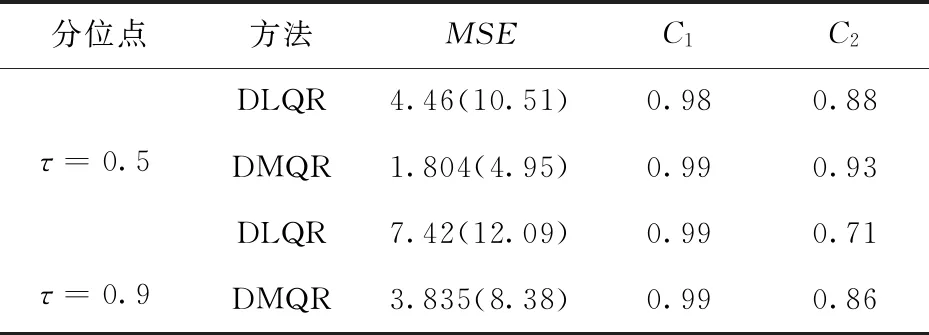
表8 高維情形不同分位點下估計結果Tab.8 Estimation results under different quantiles in the high-dimensional case

4 結論

本文在羅幼喜[9]提出的雙Lasso的基礎上改進了懲罰方法，提出了雙MCP正則化分位回歸(DMQR).通過模擬結果可以發現，不論模型是稠密模型、稀疏模型還是高度稀疏模型，改進后的方法不論是在正確選擇模型中重要變量方面還是剔除冗余變量方面均比原來的方法要好，且模型的精度更高.DMQR法對誤差有很好的穩健性，在正態分布下擬合的效果最好.在高維情況下，DMQR相對于DLQR法的優勢更大，基本上能完全選中模型中的重要預測變量，且排除冗余變量的能力也能達到90%左右，模型估計的精度更是遠遠大于DLQR法．