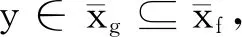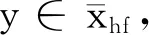保序且保等價(jià)部分變換半群上的自然偏序關(guān)系
秦 美 青
(菏澤學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,山東 菏澤 274015)
半群是最簡(jiǎn)單、最自然的一類代數(shù)系統(tǒng),半群代數(shù)理論的系統(tǒng)研究始于20世紀(jì)50年代,它是半群理論中最基本、最活躍也是成果最豐富的一部分.序理論是研究捕獲數(shù)學(xué)排序的直覺(jué)概念的各種二元關(guān)系的數(shù)學(xué)分支,它在半群的代數(shù)理論中起著非常重要的作用,序關(guān)系一直是專家學(xué)者研究的熱點(diǎn)[1-2].1952年,Vagner[3]探究了逆半群S上的自然偏序關(guān)系,給出了偏序關(guān)系的定義:
a≤b當(dāng)且僅當(dāng)a=eb,對(duì)某個(gè)e∈ES,
這里ES是指S中所有冪等元組成的集合,并且在文獻(xiàn)[3]中指出此偏序關(guān)系對(duì)于乘法是左右相容的.30年后,Hartwig和Nambooripad分別在文獻(xiàn)[4]和[5]中把逆半群上的自然偏序關(guān)系給推廣到了正則半群,給出了正則半群上自然偏序關(guān)系常用定義:a≤b當(dāng)且僅當(dāng)a=eb=bf,對(duì)某個(gè)e,f∈ES,并指出此偏序關(guān)系關(guān)于乘法不再是左右相容的.
在[6]中自然偏序關(guān)系被進(jìn)一步推廣到任意半群S,a≤b當(dāng)且僅當(dāng)a=xb=by,a=xa對(duì)某些x,y∈S1.
設(shè)X是非空集合,TX是由X上的所有完全變換做成的半群.E是X上的非平凡等價(jià)關(guān)系,文獻(xiàn)[7]刻畫了TX的由等價(jià)關(guān)系E確定的子半群
TE(X)={f∈TX:?(x,y)∈E?(f(x),
f(y))∈E}
上的正則元,描述了TE(X)中任意兩元素間的格林關(guān)系.文獻(xiàn)[8]給出了半群TE(X)上偏序關(guān)系的定義:f≤g當(dāng)且僅當(dāng)f=kg=gh,f=kf,對(duì)某些h,k∈TE(X),探討了TE(X)中兩個(gè)元素在此偏序關(guān)系下何時(shí)是相關(guān)的,給出了關(guān)于此偏序關(guān)系≤相容的元素,并刻畫了極大(小)元,覆蓋元.
設(shè)集合X是一個(gè)有限全序集,文獻(xiàn)[9]在等價(jià)關(guān)系E的每個(gè)等價(jià)類的基數(shù)都相同且所有的E-類都是凸集情況下,考慮了半群TE(X)的子半群
OE(X)={f∈TE(X):?x,y∈X,
x≤y?f(x)≤f(y)}
上的格林關(guān)系.文獻(xiàn)[10]在|X|=n,E是X上等價(jià)關(guān)系,X/E={A1,A2,…,Am}且所有E-類都是凸集的條件下,給出了半群OE(X)上自然偏序關(guān)系的定義,探討了OE(X)中兩個(gè)元素何時(shí)關(guān)于此偏序關(guān)系是相關(guān)的,給出了關(guān)于偏序關(guān)系≤相容的元素,描述了極大(小)元和覆蓋元.
設(shè)集合X(|X|≥3),PX是集合X上所有部分變換做成的半群,E是X上等價(jià)關(guān)系.文獻(xiàn)[11]刻畫了PX的由等價(jià)關(guān)系E確定的子半群
PE(X)={f∈PX:?x,y∈domf,(x,y)∈
E?(f(x),f(y))∈E}
的正則元,描述了半群PE(X)上的格林關(guān)系.文獻(xiàn)[12]在E是非平凡等價(jià)關(guān)系的前提下,研究半群PE(X)上的自然偏序關(guān)系,刻畫了關(guān)于偏序關(guān)系相容的元素,給出了極大(小)元和覆蓋元.
設(shè)集合X是一個(gè)全序集|X|=mn(m≥2,n≥3).文獻(xiàn)[13]在等價(jià)關(guān)系E包含m個(gè)等價(jià)類,每個(gè)等價(jià)類是凸集并且基數(shù)都相同情況下,考慮了半群PE(X)的子半群保序且保等價(jià)部分變換半群
POPE(X)={f∈PE(X):?x,y∈domf,
x≤y?f(x)≤f(y)}
上的正則元及其任意元素間的格林關(guān)系.
本文是在|X|=n,E是X上等價(jià)關(guān)系,X/E={A1,A2,…,Am}且所有E-類都是凸集的條件下,給出了半群POPE(X)上自然偏序關(guān)系的定義:f≤g當(dāng)且僅當(dāng)f=hg=gk,f=hf,對(duì)某些h,k∈POPE(X).研究了半群POPE(X)中兩個(gè)元素何時(shí)關(guān)于此偏序關(guān)系是相關(guān)的,給出了關(guān)于偏序關(guān)系≤相容的元素,所得結(jié)果是半群OE(X)上自然偏序結(jié)果的相應(yīng)推廣.
1 自然偏序關(guān)系的刻畫
定義1[14]集合{f-1(A):A∈X/E,A∩imf≠?},記為E(f).
定義2[15]設(shè),是X的兩個(gè)子集族.如果對(duì)每個(gè)A1∈,都存在B1∈,使得A1?B1,則稱是的細(xì)化.

引理1[12]設(shè)f,g∈PE(X),則f≤g當(dāng)且僅當(dāng)以下條件成立:
1)domf?domg,imf?img;
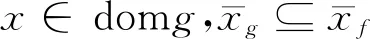
3)對(duì)任意x,y∈domf,若(g(x),g(y))∈E,則(f(x),f(y))∈E.對(duì)每個(gè)A∈X/E,存在B∈X/E,使得f(A∩domf)?g(B∩domg).
定理1設(shè)f,g∈POPE(X),則f≤g當(dāng)且僅當(dāng)以下條件成立:
1)domf?domg,imf?img;

3)若g(x)∈imf,則x∈domf且f(x)=g(x);
4)對(duì)每個(gè)A∈X/E,其中A∩domf≠?,存在保序映射φ:X/E→X/E,使得f(A∩domf)?g(φ(A∩domf)).
證明必要性.由f,g在POPE(X)中滿足f≤g,則在PE(X)中f≤g一定成立.根據(jù)引理1可得,定理1中條件1),2),3)成立.
設(shè)f≤g,則存在h,k∈POPE(X),使得f=hg=gk,f=hf,這樣
domf=domgk=k-1(imk∩domg)?domk,
從而對(duì)每個(gè)A∈X/E,若A∩domf≠?,則A∩domk≠?.由k∈POPE(X)知存在B∈X/E,使得k(A∩domf)?k(A∩domk)?B.令φ(A∩domf)=B.對(duì)每個(gè)A∈X/E,若A∩domf≠?,則存在唯一的B∈X/E,使得φ(A∩domf)=B,從而φ是良定義的.任取A1,A2∈X/E(其中A1∩domf≠?,A2∩domf≠?),不妨設(shè)A1 f(A∩domf)=gk(A∩domf)?g(B)= g(φ(A∩domf)). 充分性.假設(shè)條件1),2),3),4)成立,只需要構(gòu)造h,k∈POPE(X),使得f=hg=gk,f=hf.首先定義k如下:令domk=domf,由4)知,對(duì)每個(gè)A∈X/E,若A∩domf≠?,則存在B=φ(A∩domf),使得f(A)?g(B).任取x∈A,其中A∩domk=A∩domf≠?,記z=max{g-1(f(x))∩B}∈domg.定義k(x)=z,顯然k∈PE(X)且對(duì)任意x∈domf,gk(x)=g(z)=f(x). 下面驗(yàn)證k是保序的.任取a,c∈domk且設(shè)a 情形1若A=C,則k(a)=max{g-1(f(a))∩B}≤max{g-1(f(c))∩B}=k(c); 情形2若A k(a)=max{g-1(f(a))∩B}≤ max{g-1(f(c))∩D}=k(c), 從而k∈POPE(X). 對(duì)于h,令domh=im(g(domf))且對(duì)每個(gè)A∈X/E,其中A∩domh≠?,不妨記A∩im(g(domf))={a1,a2,…,as},其中a1 由a1 a*=maxg-1(A∩im(g(domf))), b*=ming-1(B∩im(g(domf))), 則有a* 下面驗(yàn)證f=hg,f=hf. 對(duì)任意x∈domf,由imf?img知,存在y∈domg,使得f(x)=g(y)∈imf,由條件3)知y∈domf且f(y)=g(y),從而有hf(x)=hg(y)=f(y)=f(x),所以f=hf成立. 顯然,若f,g∈POPE(X)且f≤g,則在PE(X)中一定有f≤g. 例1設(shè)集合X={1,2,3,4,5,6,7,8},E=(A1×A1)∪(A2×A2)∪(A3×A3),其中,A1={1,2,3,4},A2={5,6},A3={7,8}.令 顯然f,g∈POPE(X).下面驗(yàn)證f,g在POPE(X)中有f≤g. 1)domf?domg,imf={2,4,5,6}?img={2,3,4,5,6}. 3)通過(guò)觀察知g(1),g(2),g(4),g(5),g(6),g(7),g(8)∈imf時(shí),則有1,2,4,5,6∈domf且g(1)=f(1),g(2)=f(2),g(4)=f(4),g(5)=f(5),g(6)=f(6),g(7)=f(7),g(8)=f(8)成立,說(shuō)明了若g(x)∈imf,則x∈domf且f(x)=g(x). 4)存在保序映射φ:X/E→X/E,使得f(A1∩domf)={2,4}?g(φ(A1∩domf))=g(A1∩domg)={2,3,4}.f(A2∩domf)={5,6}?g(φ(A2∩domf))=g(A2∩domg)={5,6}.f(A3∩domf)={6}?g(φ(A3∩domf))=g(A3∩domg)={6}.綜上知,f≤g. 例1證實(shí)了f,g在POPE(X)存在偏序關(guān)系f≤g,則在PE(X)中肯定存在關(guān)系f≤g. 注若f,g∈PE(X)且f≤g,但在POPE(X)中未必有f≤g. 推論1設(shè)f,g∈POPE(X),則f≤g當(dāng)且僅當(dāng)以下說(shuō)法成立: 1)如果imf=img,則f=g; 2)對(duì)每個(gè)P∈π(f),存在P′∈π(g),使得P′?P且f(P)=g(P′); 3)如果π(f)=π(g),則f=g; 4)對(duì)每個(gè)U=f-1(A)∈E(f),其中A∈X/E,存在V∈E(g),使得V?U且f(U)=f(V)?g(V)=A∩img. 證明1)因?yàn)閕mf=img,所以對(duì)任意x∈domg,有g(shù)(x)∈imf.由定理1中條件2)知x∈domf且f(x)=g(x),由此可知domg?domf,結(jié)合domf?domg,從而有domf=domg且對(duì)任意x∈domf有f(x)=g(x),故f=g. 由2)可直接推出3). 4)由定理1中條件2)知E(g)加細(xì)E(f).任取U=f-1(A)∈E(f),其中A∈X/E.f(U)=A∩imf?A∩img.令V=g-1(A∩img)∈E(g),對(duì)任意的y∈f(U),則存在z∈V,使得y=g(z)∈imf,由定理1中3)知z∈domf且y=g(z)=f(z),這樣z∈f-1(y)?U,故V∩U≠?,所以V?U且有f(U)=f(V)?g(V)=A∩img. 定義4[16]設(shè)ρ是半群S上的一個(gè)偏序,稱元素c∈S關(guān)于ρ是左(右)相容的,如果對(duì)所有的(a,b)∈ρ,都有(ca,cb)∈ρ((ac,bc)∈ρ). 定義5設(shè)h∈POPE(X),如果存在某個(gè)A∈X/E,使得imh?A,則稱h是E-常值的. 定義6設(shè)h∈POPE(X),如果對(duì)每個(gè)A∈X/E,都有imh∩A≠?,則稱h是E-完備的. 容易得出h是E-常值的當(dāng)且僅當(dāng)E(h)=domh.h是E-完備的當(dāng)且僅當(dāng)h-1(A∩imh)=A∩domh. 定理2設(shè)h∈POPE(X),若h是E-完備的(domh=X)且對(duì)每個(gè)A∈X/E,h|A為恒等映射或常值映射,則h是左相容的. 證明設(shè)f,g∈POPE(X)且f≤g,要想說(shuō)明h是左相容的,只須證明hf≤hg. 1)因?yàn)閒,g∈POPE(X)且f≤g,所以imf?img,顯然無(wú)論h|A為恒等映射或常值映射都有imhf?imhg成立.由h是E-完備的且對(duì)每個(gè)A∈X/E,h|A為恒等映射或常值映射,則有 domhf=f-1(imf∩domh)= domf?domg=g-1(img∩domh)=domhg. 2)對(duì)任意x,y∈domhf,若(hg(x),hg(y))∈E,即存在A∈X/E,使得hg(x),hg(y)∈A,從而g(x),g(y)∈h-1(A∩imh).由h是E-完備的知g(x),g(y)∈h-1(A∩imh)∈A∈E.因?yàn)閒≤g,由定理1中條件2)可知(f(x),f(y))∈E,顯然(hf(x),hf(y))∈E成立. 若h為常值映射,分以下情況討論. 當(dāng)A≠B時(shí),則必有B>A或B 若f(x)≠f(y),則必有f(x) 若B>A,由g(y)∈A,g(x1)=f(x)∈B可知g(y) 若B 若g(x)=f(y),則g(x)∈imf.由定理1中條件3)可知x∈domf且g(x)=f(x),顯然hg(x)=hf(x)成立. 若g(x)≠f(y),由h是E-完備的知存在A∈X/E,使得g(x),f(y)∈A.因?yàn)間(x)≠f(y),所以h|A是常值映射.由推論1中4)證明知 x∈g-1(A∩img)?f-1(A∩imf), 從而有g(shù)(x),f(x)∈A,再由h|A是常值映射得hg(x)=hf(x). 4)對(duì)每個(gè)A∈X/E,若A∩domhf≠?,則顯然A∩domf≠?.由f≤g中條件4)可知,存在保序映射φ:X/E→X/E,使得f(A∩domhf)?g(φ(A∩domhf))成立.顯然hf(A∩domhf)?hg(φ(A∩domhf))成立. 綜上可知hf≤hg,從而h是左相容的. 定理3設(shè)h∈POPE(X),若h是X上的恒等映射idX,則h是右相容的. 證明假設(shè)f,g∈POPE(X)且f≤g,根據(jù)半群POPE(X)上自然偏序關(guān)系的定義,f≤g當(dāng)且僅當(dāng)f=hg=gk,f=hf,對(duì)某些h,k∈POPE(X).因此,任取f,g∈POPE(X)且f≤g,有fidX=h(gidX)=(gidX)k,fidX=h(fidX),進(jìn)而,fidX≤gidX,即恒等映射是右相容的.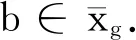



2 相容性