多穩態俘能系統的準確磁力建模方法1)

張 穎 王 偉 曹軍義，2)

* (西安交通大學現代設計及轉子軸承系統教育部重點實驗室，西安 710049)

? (鄭州大學力學與安全工程學院，鄭州 450001)

引言

高性能能量俘獲技術對狀態監測傳感器網絡的可持續性供能具有重要意義，能夠彌補傳統電池容量有限且需要及時更換的缺點.這種技術廣泛應用于汽車胎壓監測[1-2]、機械設備運行故障監測[3-4]、人體健康狀態監測[5-6]以及物聯網環境信號監測[7]等場合.非線性多穩態技術[8-10]是一種常見的能量俘獲性能提升方法，克服了傳統線性系統俘能頻帶窄的問題.該技術通過配置磁鐵引入非線性磁力，能夠使系統的共振頻率可調節，進而拓寬俘能系統的響應頻帶.

近年來，懸臂梁式多穩態壓電俘能系統[11-13]有了很大的發展.Erturk 等[14]基于Moon 和Holmes[15]提出的磁耦合懸臂梁結構設計了一種懸臂梁式非線性雙穩態壓電能量俘獲系統，對比線性系統其電壓和功率幅值分別提高了200%和800%，同時有效頻帶也顯著提高.在此基礎上，Zhou 等[16-17]通過改變外部磁鐵的旋轉角度實現了三穩態能量俘獲系統，結果表明其相對于勢阱較深的雙穩態系統能夠獲得更寬的俘能頻帶和輸出效率.此外，Huang 等[18]采用4 塊磁鐵設計了五穩態的壓電懸臂梁俘能系統，并分析了系統的動力學特性.為了研究多穩態系統中勢阱對輸出性能的影響機理，Cao 等[19]揭示了較淺的勢阱深度和較寬的勢阱范圍能提高系統在低頻激勵條件下的能量俘獲性能.雖然上述研究已經清晰地揭示了系統非線性特征與輸出性能的關系，但是多穩態系統非線性特征的正向設計方法尚未被探究.由于混沌和分岔現象的存在，多穩態系統對結構參數非常敏感，比如磁鐵配置、結構尺寸和空間位置等，結構參數微小的改變都會對系統的非線性特征產生較大的影響.因此，為了進行結構優化和參數設計，獲取預期的非線性恢復力來提高俘能性能，需要建立一種準確的非線性恢復力表征方法來定量描述結構參數與非線性恢復力關系.由于非線性恢復力中非線性特征來源于磁力，因而對多穩態系統中非線性磁力的準確建模成為了研究重點.

非線性磁力的表征方法主要包括有限元法、實驗擬合法和理論建模法.Upadrashta 和Yang[20]通過ANSYS 非線性彈簧單元對系統的磁力進行建模，進而模擬壓電懸臂梁端部磁鐵的非線性特性.雖然有限元方法能夠得到較高的準確度，但是由于計算量大，導致了對系統參數的數值優化不易.實驗擬合法是通過多項式來擬合實驗測得的數據.Ferrari 等[21]通過3 階多項式對系統非線性恢復力進行擬合，研究了多穩態磁耦合能量俘獲系統的特性，理論分析了多項式系數以及彈性剛度系數對能量俘獲系統勢能函數的影響.周生喜等[22]通過實驗測量了雙穩態和三穩態壓電懸臂梁系統的非線性恢復力離散點，并通過多項式擬合了非線性恢復力并獲得了勢能函數特性.Abdelmoula 等[23]比較了3 階、5 階和7 階多項式擬合的非線性磁力，研究表明3 階多項式會低估磁鐵所受磁力和系統的固有頻率，而高階多項式會更加準確.然而，雖然實驗擬合的方法比較準確，但是一旦系統的結構參數改變，這種方法將失效，且沒有建立起結構參數與非線性磁力的聯系.

理論建模法是通過結構參數直接建立模型來表征非線性磁力，主要包括磁偶極子法、改進磁偶極子法以及磁化電流法.磁偶極子法是由Yung 等[24]在1998 年提出，將磁鐵等效成位于磁鐵幾何中心的磁偶極子，推導了兩個磁偶極子間的磁力表達式.由于這種方法表達式簡單，計算方便，被廣泛應用于俘能系統的非線性磁力計算[25-28].然而，這種方法中只考慮了磁鐵的體積，忽略了磁鐵的形狀，只能適用于小磁鐵和大距離的場合.在此基礎上，Wang 等[29-30]提出了一種改進磁偶極子法，將磁鐵等效為兩個相對磁化表面上的磁偶極子，位于磁化表面的幾何中心，并分析了三穩態壓電懸臂梁系統的非線性磁力特征.但是，磁鐵磁化表面面積的忽略會帶來誤差，適用于磁化表面比較小的情況.此外，磁化電流法是將永久磁鐵的磁化強度等效成電流，然后運用畢奧薩伐爾定律求解等效電流在空間中產生的磁場強度，進而求解永久磁鐵之間的磁力[31].Leng 等[32]采用等效電流法分析了壓電式磁耦合懸臂梁能量俘獲系統的磁力特性，并應用到三穩態系統的磁力建模，但是將系統端部磁鐵的等效電流集中在所在面的中心，忽略了外部磁鐵在端部磁鐵表面產生的磁場強度分布情況.

為了克服以上建模方法的局限性，提出一種多穩態系統非線性磁力的準確建模方法，以更好地刻畫多穩態俘能系統的輸出性能.本文基于磁荷理論以及磁鐵間的空間相對位置推導了多穩態俘能系統的非線性磁力模型，通過實驗驗證了不同結構參數下非線性磁力計算的準確性，分析了不同系統結構參數對多穩態系統非線性特征和響應電壓的影響，并進行了參數分析與優化，以期為多穩態系統的結構設計提供理論基礎.本文提出的多穩態俘能系統準確磁力建模方法具有更廣泛的適用場合，采用磁荷理論并未對磁力建模進行簡化和忽略，因而可以適用任意尺寸和空間位置的磁力計算.

1 多穩態俘能系統的建模

圖1 為常見的壓電雙穩態俘能結構，包括壓電片、懸臂梁、端部磁鐵和外部磁鐵.其中，端部磁鐵與外部磁鐵相對布置，承受相斥的磁力，使得系統存在兩個穩態點.若存在兩塊外部磁鐵分布在兩側時，系統則變為三穩態系統，存在3 個穩態點.

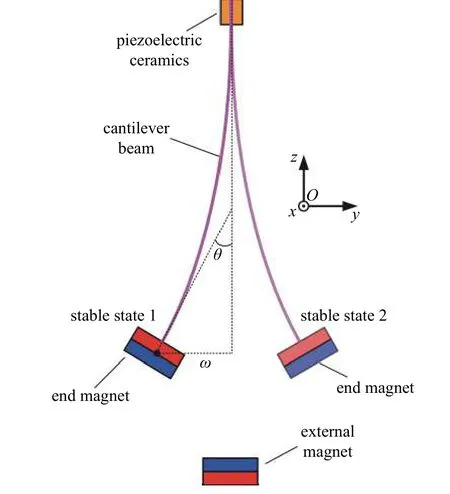
圖1 壓電雙穩態俘能結構Fig.1 Piezoelectric bi-stable energy harvester

根據哈密頓原理和歐拉梁理論，考慮懸臂梁的一階模態，壓電多穩態系統的控制方程為[33-34]

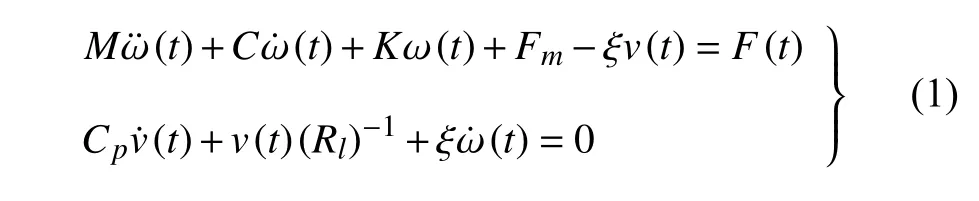
式中，M為系統的等效質量，C為系統的等效阻尼系數，K為系統的等效剛度，ξ為機電耦合系數，Cp為壓電片的等效電容，Rl為外部電路負載，v(t)為壓電陶瓷的響應電壓，ω(t)為懸臂梁的橫向位移，F(t)為外部激勵，Fm為非線性磁力.

多穩態系統的非線性恢復力可以看作是懸臂梁彈力和磁力的和，即

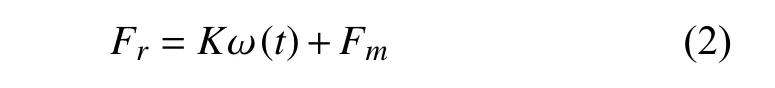
在以往的研究中已經通過實驗驗證了在小范圍內懸臂梁彈力可以看作是線性，根據材料力學理論，懸臂梁彈力的剛度可以表達為

式中，E為懸臂梁的彈性模量，I為懸臂梁截面的慣性矩，l為懸臂梁長度.

要求解非線性恢復力，需要準確計算出多穩態系統中的非線性磁力Fm，這里采用磁荷法推導多穩態系統的磁力表達式.

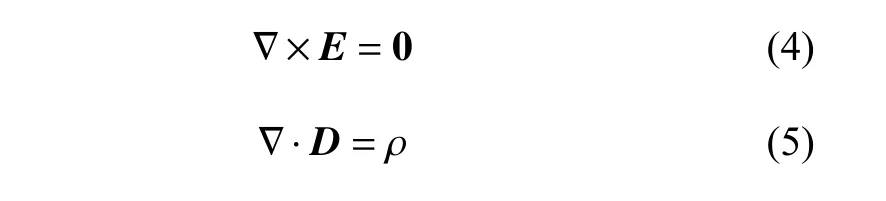
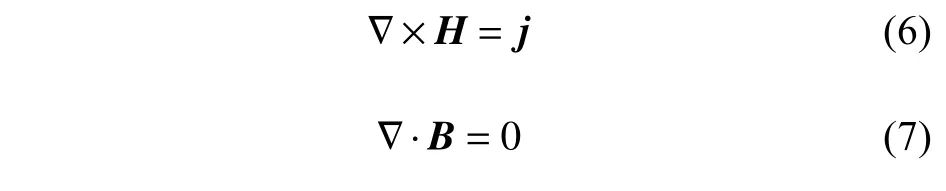
式(4)～式(7)是麥克斯韋方程組的微分形式，其中式(4)和式(5)描述電場，式(6)和式(7)描述磁場，E為電場強度，D為電位移，ρ為電荷密度，H為磁場強度，j為電流密度，B為磁通密度.

永久磁鐵可以假設不存在電流密度，則j=0.此時，永久磁鐵產生的磁場為無旋場，式(6)可以改寫為

由于無旋場的積分與路徑無關，則可以通過定義磁標量勢φm計算磁場強度

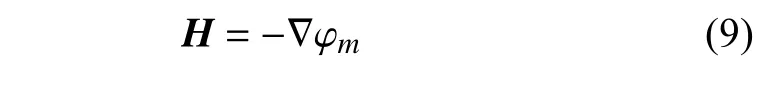
同樣地，通過在無旋場中定義兩任意磁荷之間的磁勢能進而可以計算磁力為

因此，要求解磁鐵之間的磁力，需要先計算出兩磁鐵之間的磁勢能.磁荷法通過將永久磁鐵的磁化強度等效為分布在兩個磁化表面相反極性的磁荷，其磁荷密度的幅值等于磁鐵磁化強度的幅值.通過磁場庫倫定律可以計算兩磁荷密度之間的磁勢能，然后對整個磁鐵表面的磁荷進行積分，進而得到兩磁鐵之間的總勢能.

對于如圖2 所示的雙穩態系統磁鐵空間位置，端部磁鐵和外部磁鐵的磁化強度都為M，沿x，y，z，3 個方向的尺寸分別為2a×2b×2c和2A×2B×2C，其中磁化表面的尺寸分別是2a×2b和2A×2B.端部磁鐵和外部磁鐵表面的磁荷密度分別定義為

圖2 雙穩態系統磁鐵空間位置Fig.2 Spatial position of magnets for bi-stable system

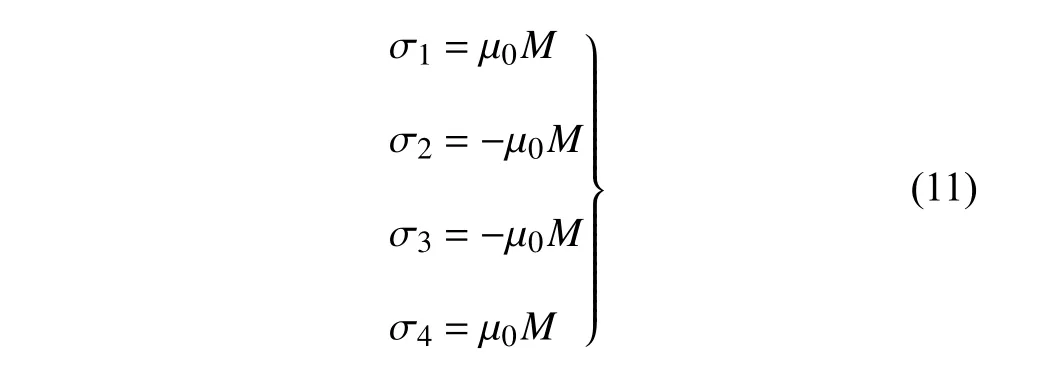
式中，μ0為真空中的磁導率.

根據磁場庫侖定律，磁荷密度為σ1和σ3的磁鐵表面之間的磁勢能為

式中，r為兩磁荷之間的距離.

對所有磁化表面的磁勢能進行求和，得到端部磁鐵和外部磁鐵之間的總磁勢能為

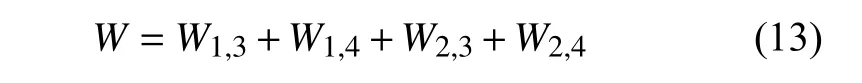
對于兩塊相對旋轉的方形磁鐵，Charpentier 和Lemarquand[35]推導了完整的磁力計算表達式.在此基礎上，要計算圖2 所示雙穩態能量俘獲系統所受磁力，需要獲取兩磁鐵之間的空間位置，也就是兩磁鐵之間的相對距離和相對轉角.以懸臂梁處于y負半軸為例，首先容易得到端部磁鐵與外部磁鐵沿逆時針方向的相對旋轉角度為π-θ.其次，對于兩磁鐵之間的相對距離，設定圖示端部磁鐵和外部磁鐵的頂點分別為P1和P2，根據坐標系和幾何關系可得

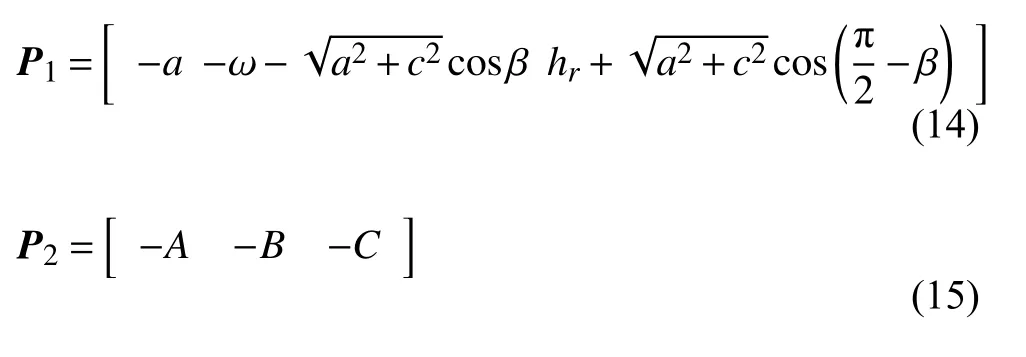
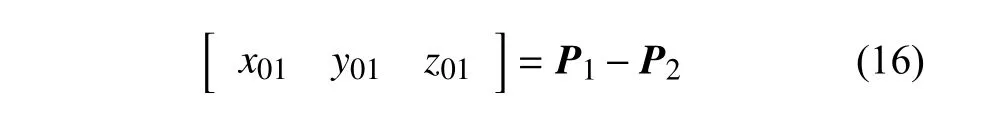
基于上述系統參數以及磁鐵間相對距離和轉角，進而能夠計算兩磁鐵之間的磁力大小為

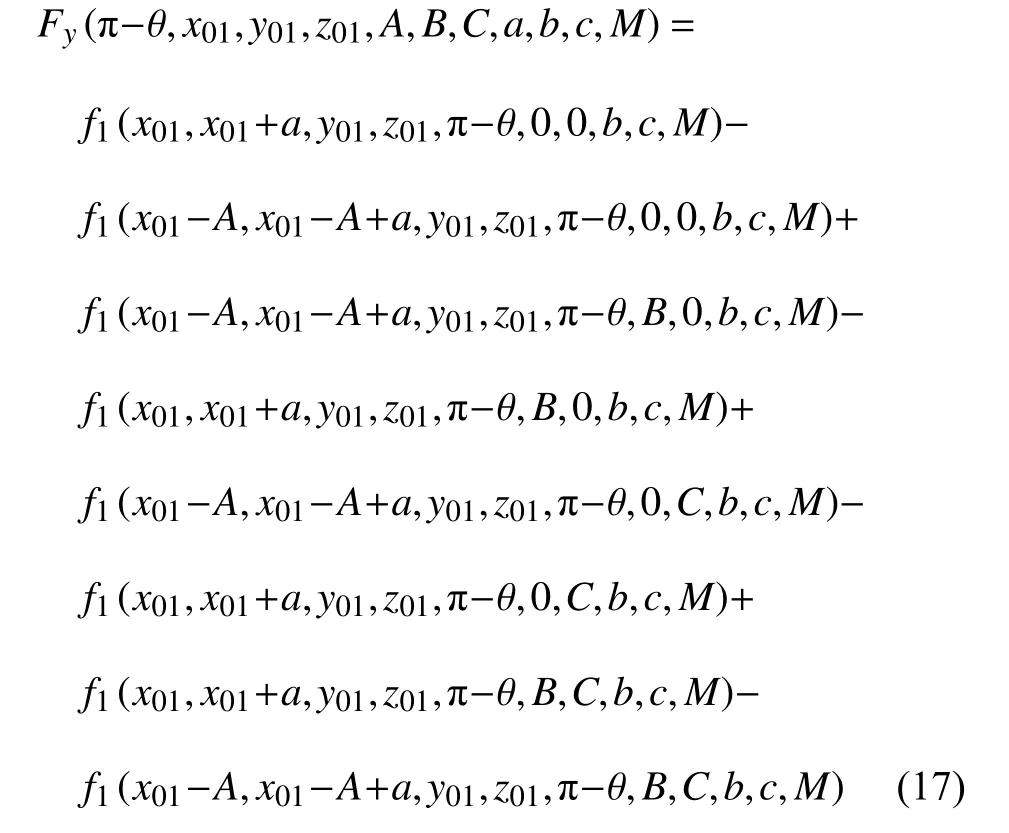
式中

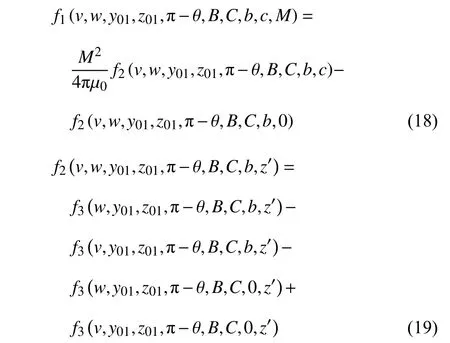
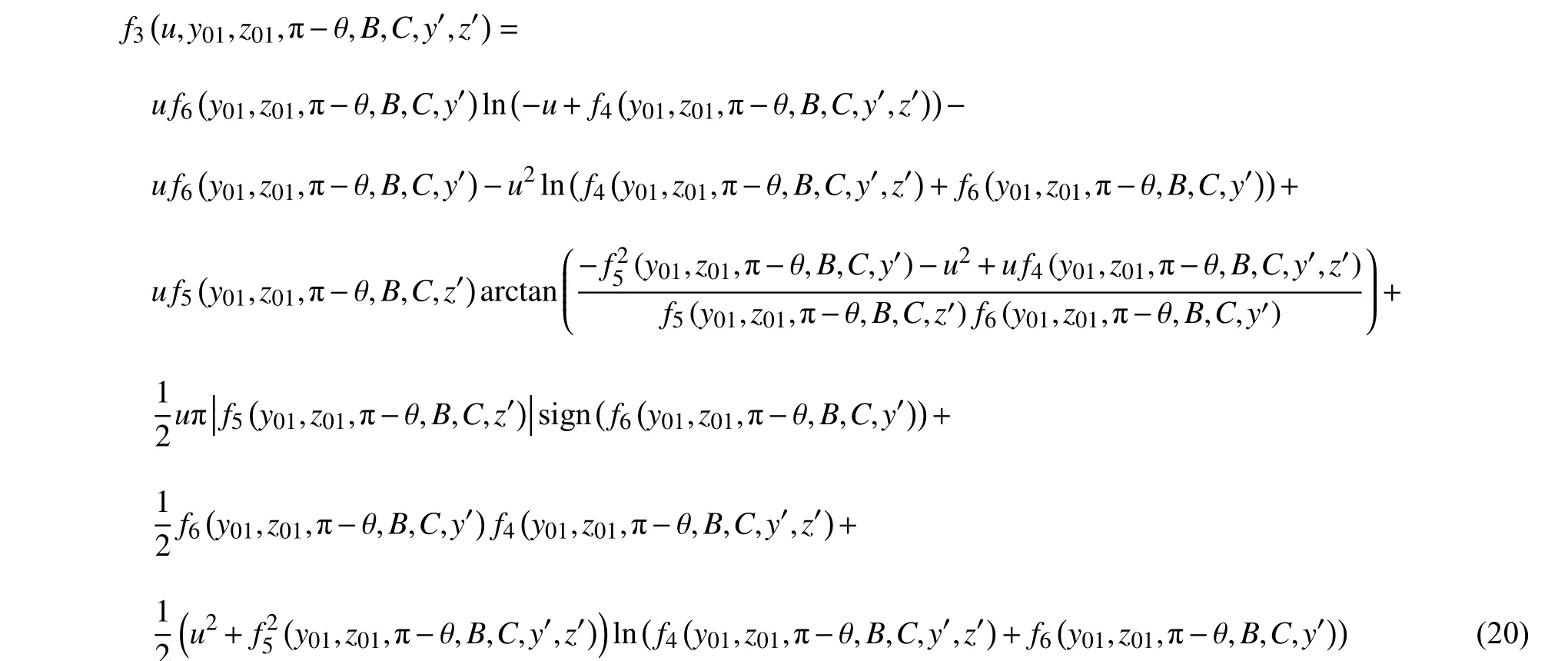
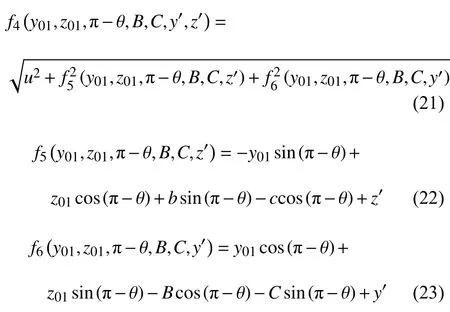
式中，f1～f6為中間函數，u，v，w，y'和z'為中間變量.

此外，由于懸臂梁端部磁鐵的位置隨著位移變化而變化，需要建立懸臂梁端部轉角θ以及沿z方向長度隨位移ω的變化關系，因此有[36]

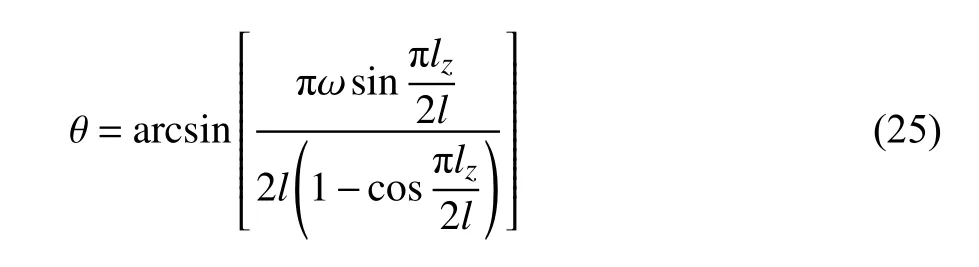
式中，lz為懸臂梁在位移為ω時沿z方向的長度，l為懸臂梁原始長度.因此，懸臂梁沿z方向長度的變化為

對于三穩態系統而言，非線性磁力的求解與雙穩態系統類似，需要分別計算兩塊外部磁鐵對端部磁鐵產生的磁力，然后對磁力進行疊加得到總磁力.

2 非線性磁力的實驗驗證

2.1 實驗平臺搭建

為了驗證本方法計算多穩態俘能系統磁力的準確性，搭建了圖3 所示非線性磁力測量實驗平臺，包括測力計(force gauge model M5-2)、激光位移傳感器(Panasonic HL-G105-A-C5)、外部磁鐵、端部磁鐵、懸臂梁和螺栓.測力計直接連在外部磁鐵上，通過調節螺栓可以記錄不同位置下端部磁鐵所受的磁力，同時激光位移傳感器測量端部磁鐵的位移.懸臂梁端部磁鐵的尺寸為10 mm × 10 mm × 4 mm，外部磁鐵的尺寸為10 mm × 10 mm × 10 mm.磁鐵的材料為N50，磁化強度為1.46 T.懸臂梁材料為不銹鋼，原始長度為120 mm.

圖3 非線性磁力測量實驗Fig.3 Experimental setup of nonlinear magnetic force

2.2 非線性磁力的驗證結果

圖4 為雙穩態系統的非線性磁力驗證，比較了實驗測量(experiment)、本文方法(this model)、磁偶極子法(M1)、磁化電流法(M2)和改進磁偶極子法(M3)的磁力大小.懸臂梁端部磁鐵與外部磁鐵的豎直距離h為17 mm.可以看出，本文方法與實驗測量的磁力吻合較好，而由于磁偶極子法、磁化電流法和改進磁偶極子法存在特定的適用場合，其計算誤差都比較大.本文方法計算的磁力峰值為0.375 8 N，實驗測量的磁力峰值為0.36 N，誤差為4.3%.磁偶極子法計算的磁力峰值為0.421 4 N，誤差為17.06%.磁化電流法計算的磁力峰值為0.319 3 N，誤差為1 1.2 9%.改進磁偶極子法計算的磁力峰值為0.495 5 N，誤差為37.60%.此外，當位移較大時，磁偶極子法和改進磁偶極子法的誤差會越來越小，但是磁化電流法的誤差一直保持較大.

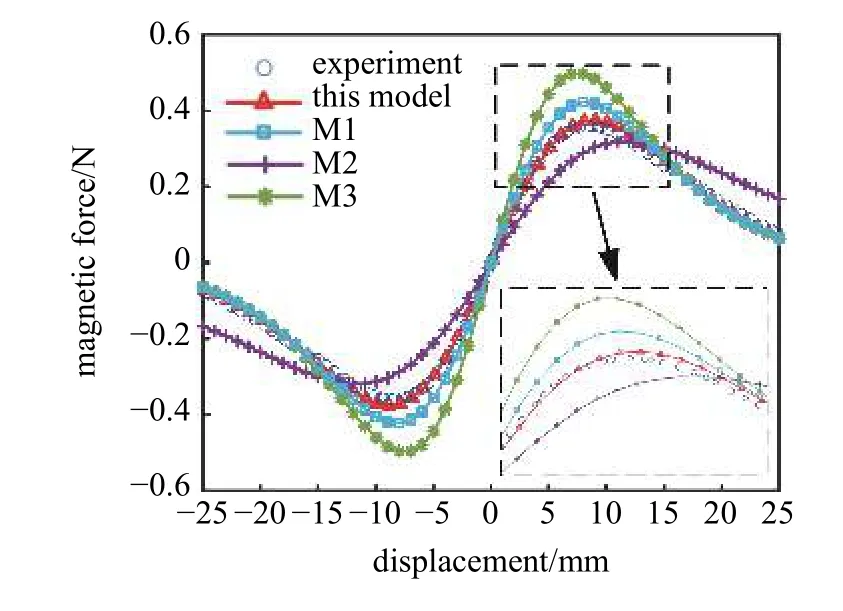
圖4 雙穩態系統非線性磁力Fig.4 Nonlinear magnetic force in bi-stable system

三穩態系統通常需要兩塊外部磁鐵實現，由于這里研究的是對稱三穩態系統，兩塊外部磁鐵關于系統中心對稱.因此，定義兩外部磁鐵之間的距離為2d，則每塊外部磁鐵到系統中心的水平距離為d(沿y方向的距離).圖5 為三穩態系統的非線性磁力驗證，比較了實驗測量(experiment)、本文方法(this model)、磁偶極子法(M1)、磁化電流法(M2)和改進磁偶極子法(M3)計算的磁力大小.懸臂梁端部磁鐵與外部磁鐵的豎直距離h為12 mm，外部磁鐵到系統中心的水平距離d為10 mm.可以看出，本文方法計算的磁力與實驗測量結果最吻合.本文方法計算的磁力峰值為0.669 4 N，實驗測量的磁力峰值為0.628 6 N，誤差為6.49%.磁偶極子法計算的磁力峰值為0.860 7 N，誤差為36.92%.磁化電流法計算的磁力峰值為0.102 7 N，誤差為83.66%.改進磁偶極子法計算的磁力峰值為1.167 78 N，誤差為85.77%.

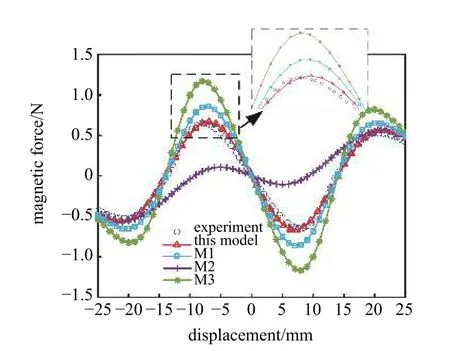
圖5 三穩態系統非線性磁力Fig.5 Nonlinear magnetic force in tri-stable system

綜上所述，通過本文方法計算得到的雙穩態和三穩態系統磁力與實驗測量結果比較吻合，驗證了本文方法的有效性.

3 結構參數對非線性特征的影響

為了提高多穩態系統的俘能性能，對系統進行參數優化具有重要的意義.因此，基于本文方法能夠研究不同結構參數對系統勢阱特性以及響應電壓的影響，并獲取多穩態系統的最優輸出性能.雙穩態結構和三穩態結構的系統等效質量M為1.7 g、等效阻尼系數C為2.4 mN·s/m、機電耦合系數ξ為-8.87 μN/V、壓電片的等效電容Cp為8.301 5 nF、外部負載R為10 MΩ.激勵為1～20 Hz 的升頻掃頻信號，幅值為0.3 g.

3.1 雙穩態結構參數分析

3.1.1 豎直距離影響

圖6 為豎直距離h對雙穩態系統勢阱的影響，h從30 mm 變化到40 mm.可以看出，當h為30 mm時，系統為勢阱較深的雙穩態系統.隨著h逐漸增大到36 mm 時，兩側勢阱變得越來越淺，且勢阱寬度越來越窄，但始終都保持為雙穩態系統.然而，當h增大到38 mm 時，系統由雙穩態過渡成單穩態.此后，當h繼續增大到40 mm 時，系統依然為單穩態系統，且勢阱寬度越來越窄.由此可見，雙穩態系統的臨界位置處于h從36～38 mm 之間.

圖6 豎直距離h 對雙穩態系統勢阱的影響Fig.6 Influence of vertical distance h on bi-stable potential well

圖7 給出了豎直距離h對雙穩態系統響應電壓的影響，選取h的變化范圍為30～50 mm，間隔為5 mm.由圖可知，當h為30 mm 時，激勵不足以使系統跨越勢阱，只產生位移較小的勢阱內運動，因而響應電壓較小，峰值僅為10 V 左右.當h增大為35 mm時，響應電壓的幅值達到最大為46 V 左右，且頻帶也最寬，這是由于此時雙穩態系統的勢阱較淺.當h從40 mm 增大到50 mm 的過程中，單穩態系統勢阱會逐漸變窄，因而響應電壓的幅值略有下降，俘能頻帶明顯變窄，效率降低.

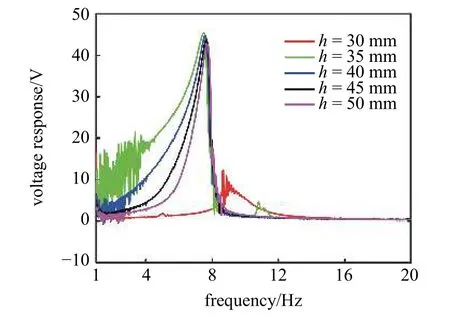
圖7 豎直距離h 對雙穩態系統響應電壓的影響Fig.7 Influence of vertical distance h on bi-stable voltage response

為了量化研究豎直距離h對響應電壓頻帶寬度的影響，設定響應電壓10 V 以上作為有效頻帶，并得到了如圖8 所示的雙穩態系統頻帶變化.由圖可知，當豎直距離h從32 mm 增大到34 mm 時，系統的帶寬從0.6 Hz 增加到6.98 Hz.隨著磁鐵間豎直距離h的進一步增大，系統的帶寬逐漸減小.當豎直距離h為50 mm 時，系統的帶寬為2.098 Hz.

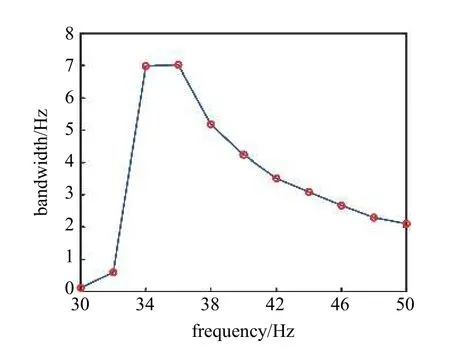
圖8 豎直距離h 對雙穩態系統頻帶影響Fig.8 Influence of vertical distance h on bandwidth of bi-stable system

為了更好地研究系統的響應特性，圖9 給出了不同豎直距離h的雙穩態系統相軌跡圖.由圖可知，當豎直距離h為30 mm 時，系統主要為勢阱內運動.當豎直距離h為35 mm 時，系統主要為跨越勢阱的大幅值運動.當豎直距離h為40 mm 時，此時系統為單穩態系統，系統也能產生幅值較大的運動.

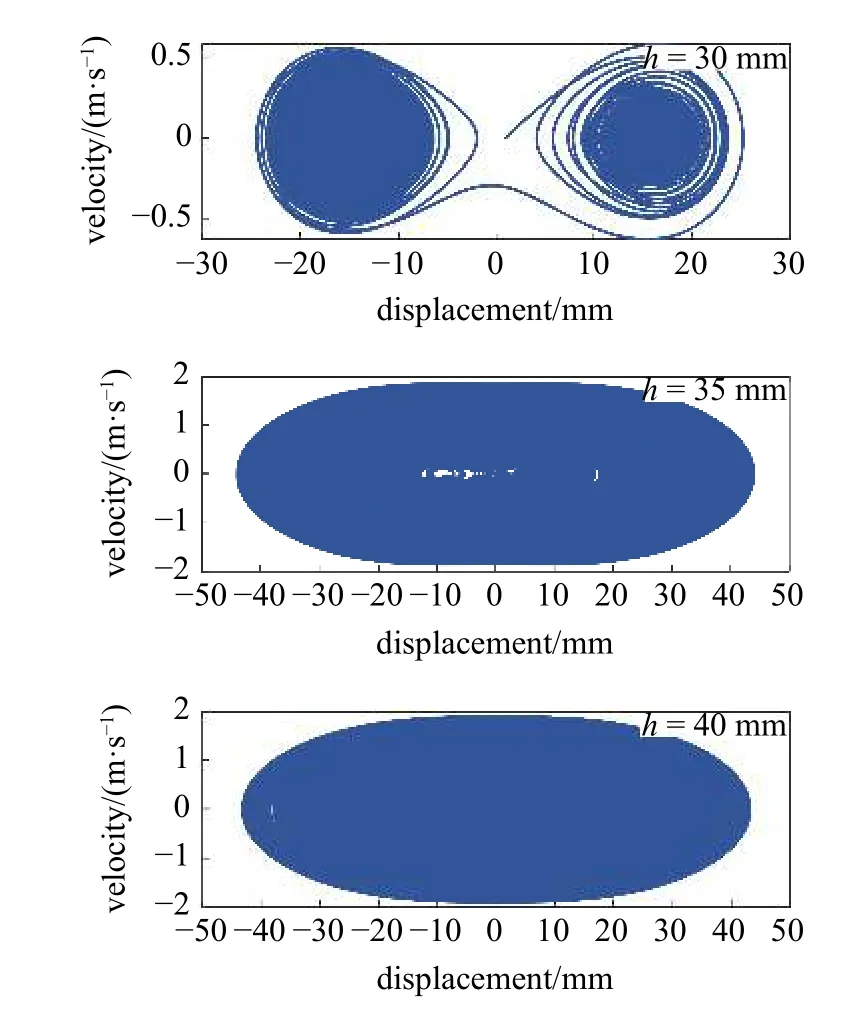
圖9 不同豎直距離h 的雙穩態系統相軌跡圖Fig.9 Phase trajectory of bi-stable system under different vertical distance h

3.1.2 參數優化

為了獲取雙穩態系統結構的最優參數，對豎直距離h進行參數掃描得到了如圖10 所示均方電壓的變化規律，h的變化范圍為15～60 mm，間隔為1 mm.首先給定幅值為0.3 g 的1～20 Hz 掃頻激勵，獲取不同豎直距離h下的響應電壓頻響關系，然后計算頻域均方電壓，以此作為參數優化目標，綜合考慮了響應電壓幅值和頻帶的影響.由圖可知，當h從15 mm 增大到33 mm 時，均方電壓保持在較低的水平，不超過3 V.然而，當h變化到34 mm 時，均方電壓突然增大到10.22 V.此后，隨著h的進一步增大，均方電壓逐漸降低，但是也保持在較高的水平.

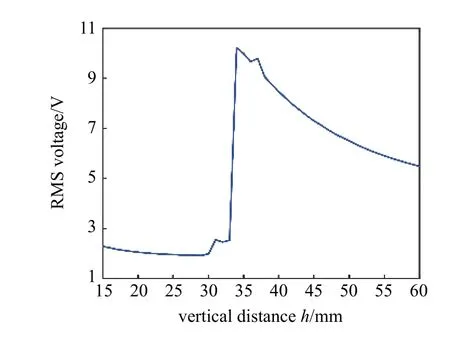
圖10 雙穩態系統最優豎直距離hFig.10 The optimal vertical distance h for bi-stable system

3.2 三穩態結構參數分析

3.2.1 豎直距離影響

圖11 為豎直距離h對三穩態系統勢阱的影響，h從26 mm 變化到36 mm.可以看出，當h為26 mm時，三穩態系統的外側勢阱最深.隨著h增大到30 mm 時，勢阱逐漸變淺，且勢阱寬度變窄，但始終為三穩態系統.然而，當h增大到32 mm 時，系統由三穩態過渡為單穩態.當h繼續增大時，系統依然為單穩態系統，且勢阱寬度越來越窄.因此，三穩態系統臨界位置處于h從30～32 mm 之間.

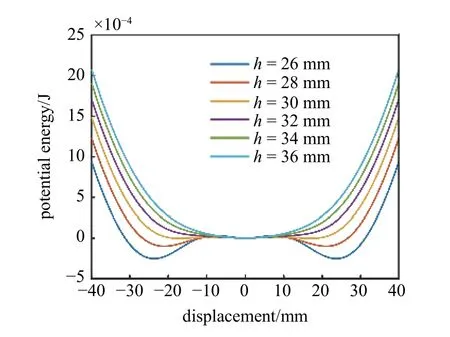
圖11 豎直距離h 對三穩態系統勢阱的影響Fig.11 Influence of vertical distance h on tri-stable potential well

圖12 給出了豎直距離h對三穩態系統響應電壓的影響，h的變化范圍從25～45 mm，間隔為5 mm.可以看出，當h為25mm 時只產生位移較小的勢阱內運動，因而響應電壓較小，峰值僅為20 V 左右，這可能是由于三穩態勢阱較深，激勵不足使系統產生跨越勢阱運動.當h增大為30 mm 時，響應電壓的幅值達到最大為48 V 左右，且頻帶也最寬，此時系統的勢阱較淺，容易產生跨越勢阱運動.當h從35 mm增大到45 mm 時，系統響應電壓的幅值略有下降，但是俘能頻帶明顯變窄，效率降低.這是由于此過程中系統始終為單穩態，且勢阱的寬度會隨著h的增大而變窄.

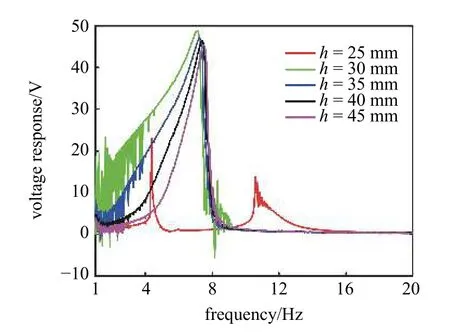
圖12 豎直距離h 對三穩態系統響應電壓的影響Fig.12 Influence of vertical distance h on tri-stable voltage response

圖13 所示為豎直距離h對三穩態系統頻帶的影響，設定響應電壓10 V 以上作為有效頻帶.由圖可知，當豎直距離h從25 mm 增大到30 mm 時，系統的帶寬從3.6 Hz 增加到6.52 Hz.此后，系統的帶寬逐漸減小.當豎直距離h為60 mm 時，系統的帶寬為1.679 Hz.

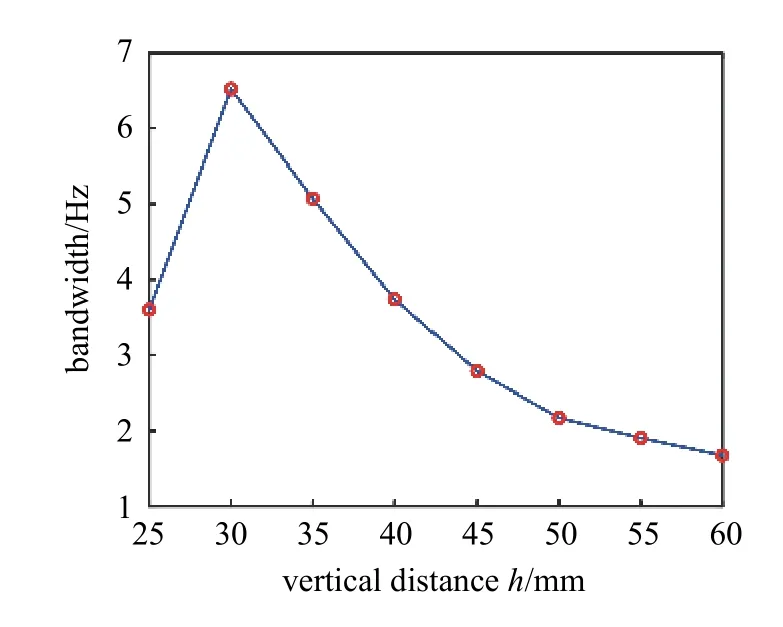
圖13 豎直距離h 對三穩態系統頻帶影響Fig.13 Influence of vertical distance h on bandwidth of tri-stable system

圖14 給出了不同豎直距離h的三穩態系統相軌跡圖.由圖可知，當豎直距離h為25 mm 時，系統的主要為幅值較小的勢阱內運動.當豎直距離h為30 mm 時，系統主要為跨越3 個勢阱的大幅值運動.當豎直距離h為40 mm 時，此時單穩態系統也能產生幅值較大的運動.

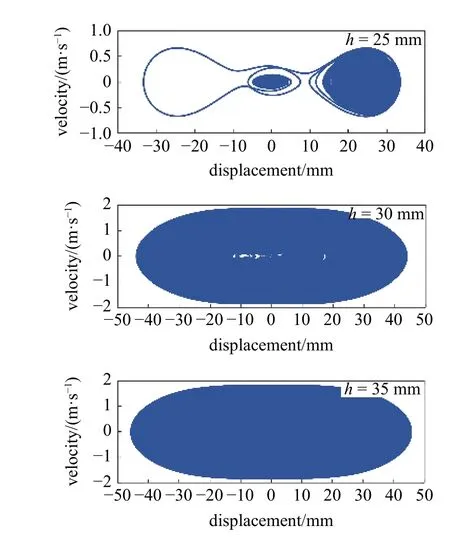
圖14 不同豎直距離h 的三穩態系統相軌跡圖Fig.14 Phase trajectory of tri-stable system under different vertical distance h

3.2.2 水平距離影響

圖15 為水平距離d對三穩態系統勢阱的影響，d從7 mm 變化到12 mm.可以看出，當d從7 mm增加到8 mm 時，系統始終為三穩態，內側勢阱較小，外側勢阱逐漸變淺.隨著d增大到9 mm 時，系統變為單穩態.當d繼續增大時，系統依然為單穩態系統，且勢阱寬度越來越窄.因此，三穩態系統的臨界位置處于d從8～9 mm 之間.

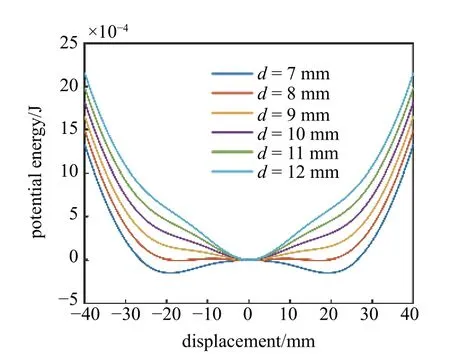
圖15 水平距離d 對三穩態系統勢阱的影響Fig.15 Influence of horizontal distance d on tri-stable potential well

圖16 給出了水平距離d對三穩態系統響應電壓的影響，d的變化范圍從4～12 mm，間隔為2 mm.可以看出，當d為4 mm 和6 mm 時，系統的響應電壓較小，峰值僅為16 V 和28 V 左右，且頻帶較窄.這可能是此時三穩態系統的勢阱較深，難以產生跨勢阱的運動.當d增大為8 mm 時，響應電壓的幅值達到最大為48 V 左右，且頻帶也最寬，此時由于三穩態系統的勢阱較淺，容易產生跨越勢阱運動.當d繼續從10 mm 增大到12 mm 時，系統響應電壓較低，但是俘能頻帶明顯變窄.這是由于此過程中系統始終為單穩態，且勢阱的寬度會隨著d的增大而變深且變窄.

圖16 水平距離d 對三穩態系統響應電壓的影響Fig.16 Influence of horizontal distance d on tri-stable voltage response

圖17 所示為水平距離d對三穩態系統頻帶的影響，設定響應電壓10 V 以上作為有效頻帶.由圖可知，當水平距離d從7 mm 增大到8 mm 時，系統的帶寬從0.534 Hz 增加到6.524 Hz.此后，系統的帶寬下降很快.當水平距離d為10 mm 時，系統的帶寬僅為0.72 Hz.

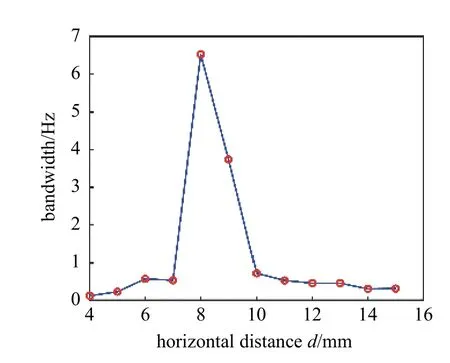
圖17 水平距離d 對三穩態系統頻帶影響Fig.17 Influence of horizontal distance d on bandwidth of tri-stable system

圖18 給出了不同水平距離d的三穩態系統相軌跡圖.由圖可知，當水平距離d為4 mm 時，系統為幅值較小的勢阱內運動.當水平距離d為8 mm時，系統主要為跨越3 個勢阱的大幅值運動.當水平距離d為12 mm 時，此時單穩態系統為幅值較小的運動.

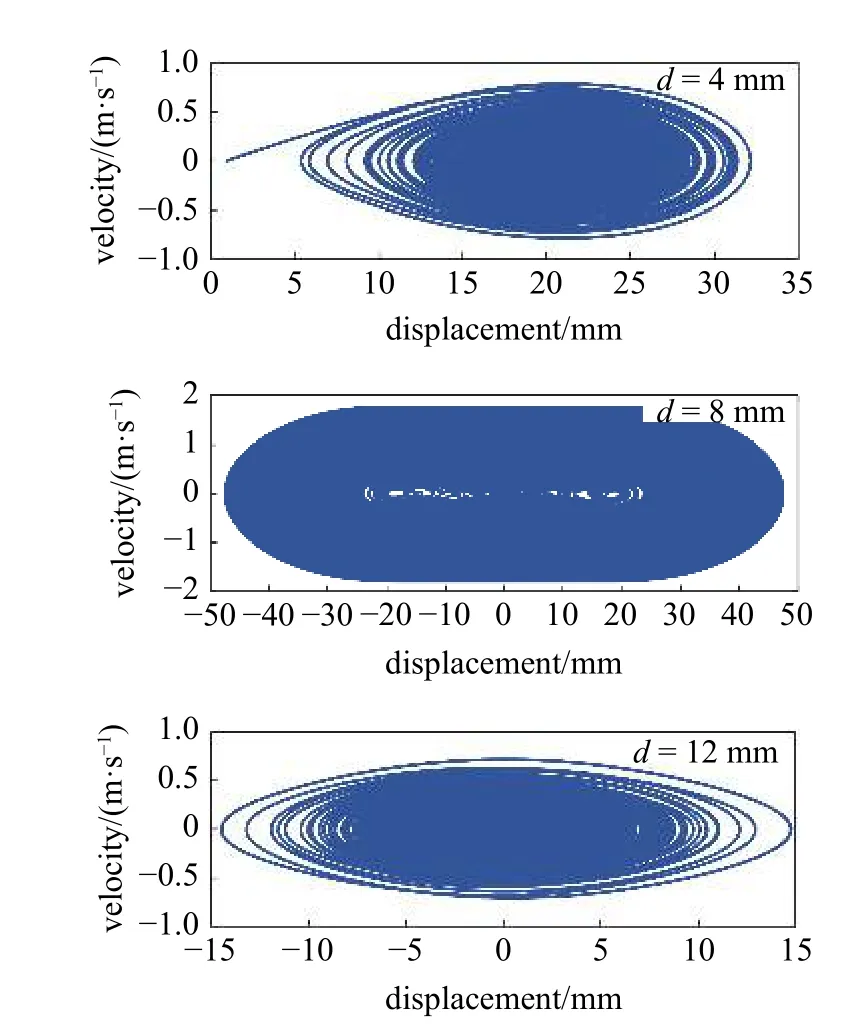
圖18 不同水平距離d 的三穩態系統相軌跡圖Fig.18 Phase trajectory of tri-stable system under different horizontal distance d

3.2.3 參數優化

為了獲取三穩態系統最優的結構參數，對豎直距離h和水平距離d進行了參數掃描得到了圖19所示均方電壓的變化規律，h的變化范圍為10～60 mm，d的變化范圍為1～20 mm，間隔都為1 mm.由圖可知，隨著h地增大，均方電壓剛開始增長比較緩慢，但是當到達某個值后會出現突然地增加，然后在呈現逐漸下降的趨勢.而當d增加時，均方電壓呈現較緩的上升趨勢，然后再逐漸下降.此外，當d為8 mm 且h為28 mm 時，系統的最大均方電壓為12.7 V.

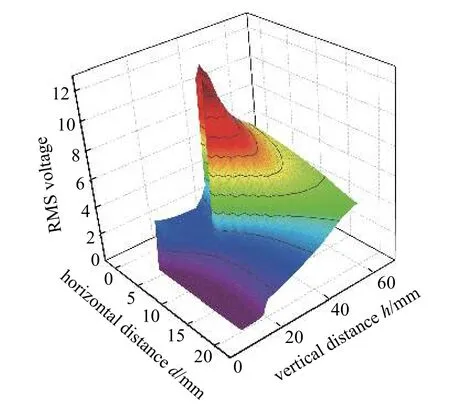
圖19 三穩態系統參數優化Fig.19 Parameters optimization of tri-stable system

4 結論

針對多穩態系統結構設計與參數優化困難的問題，提出了一種多穩態俘能系統的準確磁力建模方法.通過計算多穩態系統中端部磁鐵和外部磁鐵的相對距離和相對轉角推導了磁鐵間的相對位置，采用磁荷理論建立了系統的非線性磁力模型.通過實驗驗證了本方法預測非線性磁力的準確性，雙穩態系統和三穩態系統的磁力峰值誤差分別僅為4.3%和6.49%.

此外，基于本方法探究了多穩態系統結構參數對系統勢能和響應電壓的影響機理，找出了雙穩態系統和三穩態系統的臨界位置，同時優化結構參數得到了最優輸出性能.首先，對于雙穩態系統，隨著豎直距離h增大，雙穩態會變為單穩態，臨界位置在h為36～38 mm 之間，且當h為34 mm 時存在最大均方電壓為10.22 V.其次，對于三穩態系統，隨著豎直距離h增大，三穩態會變為單穩態，臨界位置在h為30～32 mm 之間;隨著水平距離d增大，三穩態會變為單穩態，臨界位置在d為8～9 mm 之間.當d為8 mm 且h為28 mm 時，系統最大均方電壓為12.7 V.

由于實際多穩態俘能系統往往具有確定的材料參數和外界激勵，基于提出的模型可以針對性地優化其結構參數.首先基于本模型可以預測系統的非線性恢復力以及勢阱，然后通過求解系統非線性動力學方程得到響應電壓的幅值和頻帶.因此，在給定激勵譜條件下，以響應電壓幅值和帶寬為優化目標，可以優化豎直距離和水平距離等結構參數.