基于偽均質流理論的預應力管道壓漿技術研究
舒小娟,駱藝立,沈明燕,朱懿武
(湖南科技大學 土木工程學院,湖南 湘潭 411201)
預應力管道壓漿不飽滿導致預應力筋銹蝕是影響預應力混凝土橋梁質量的主要原因之一[1],因此研究預應力管道壓漿技術,有助于預應力混凝土橋梁的持續健康發展,具有重要的經濟效益和社會效益.
眾多學者針對預應力管道壓漿的相關研究,主要分為2 類,一類是預應力管道壓漿質量檢測研究,其中,沖擊回波法、超聲波探測法、電磁波探測法、紅外熱成像檢測法是目前常用的預應力管道壓漿密實度無損檢測方法.楊雅勛等[2]利用沖擊回波法對預應力管道壓漿缺陷檢測進行探究.譚少海等[3]對比了各種常用的檢測方法的優缺點.龔士林等[4]提出了一種基于分布式光纖傳感器的預應力管道壓漿質量檢測方法,該方法可近似求解出所對應的壓漿密實度.另一類是對提高預應力管道壓漿質量的研究.姚日高[5]在連續梁工程項目中使用了真空輔助壓漿技術以及可消除人為因素對壓漿質量影響的后張法預應力智能化施工技術[6].劉柳奇[7]提出了循環智能壓漿技術的概念,在此基礎上,房慧明等[8]還通過預應力管道循環壓漿試驗和數值分析證明了循環壓漿能有效提高壓漿質量.
為提高預應力管道壓漿質量,本文將偽均質流理論、漿體管道運輸的相關理論[9-10]及固液兩相流理論[11]運用于預應力管道壓漿技術,以達到指導壓漿的目的.
1 水泥漿體管道輸送計算理論
1.1 流動狀態的界定與相關速度的計算
壓漿漿體為沉降性漿體,其中固體顆粒的流動狀態會因為漿體平均速度的改變而改變[9].為了使壓漿過程穩定,要保證漿體具有一定的流速,使固體顆粒不僅處于懸浮狀態,且固體顆粒與液體兩部分的速度接近甚至相同,使固液混合物進入偽均質流狀態,并可視為單一流體,該界限速度稱為均質流界限速度VH.當漿體運動的速度介于均質流界限速度VH和浮游界限速度VB之間時,此時一部分固體顆粒處于跳、滑移狀態,另一部分固體顆粒處于懸浮狀態.可用Newitt 公式計算固體顆粒的浮游界限速度VB與均質流界限速度VH,公式如下[12]:

其中,Vt為固體顆粒沉降速度;D為管道內徑.Vt的求解由Swanson 公式得出,即
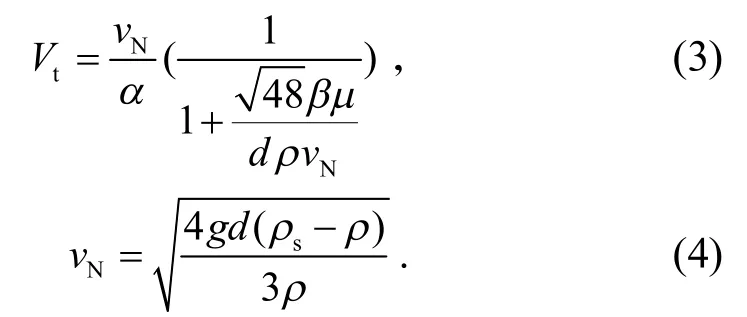
其中,α、β為斯萬遜形狀系數;ρ為液體密度;ρs為固體顆粒密度;vN為動粘性系數;g為重力加速度;d為固體顆粒直徑,本文用固體顆粒的球等價直徑de替代d的取值;μ為粘性系數.
當固體顆粒在體積濃度為C的液體中進行集體沉降時,因為固體顆粒在沉降的過程中會互相影響,所以一群固體顆粒一起沉降時的沉降終速度會小于單個粒子的沉降終速度,該速度稱為干涉沉降終速度,用vh表示,其計算公式為
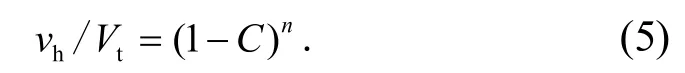
其中,n為固體顆粒的雷諾數(Rep=dVtρ/μ)的相關函數.當Rep<100 時,使用Wallis 公式:

當Rep>100 時,使用佐藤博公式[12]:

其中,

1.2 偽均質流各成分速度和水力坡度解析模型
漿體中各成分平均速度相關求解公式[9-10]為

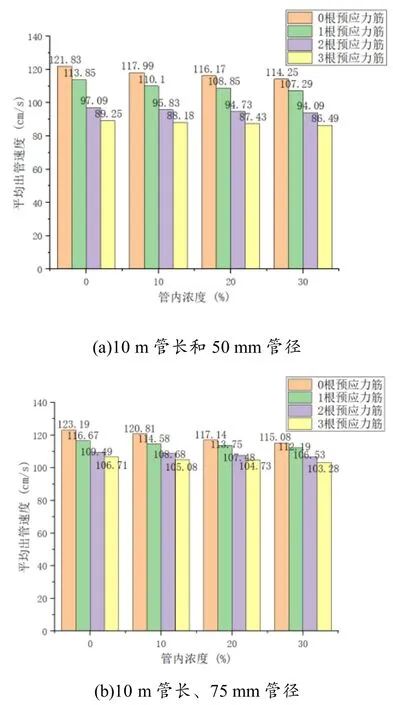
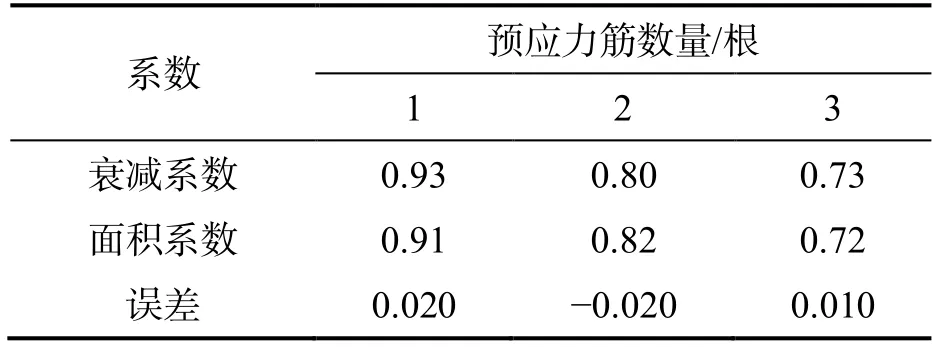
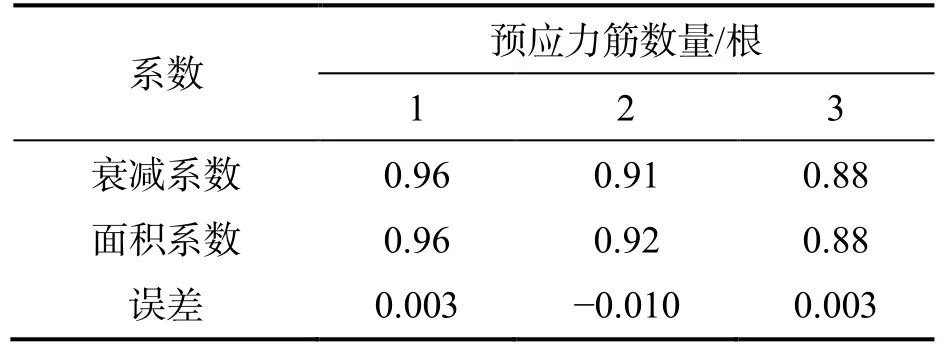
其中,Vs、Vw、Vm分別為固體顆粒、清水、非均質流的運動速度,當漿體處于偽均質流運動狀態時Vs≈Vw≈Vm;V為清水動量交換前的平均速度;ff為單個固體顆粒上的摩擦力,當固體顆粒處于懸浮狀態時ff=0;q為管道內固體顆粒的平均濃度;La為固體顆粒的加速距離;λ為管摩擦系數;δ為固體顆粒的密度與液體的密度之比;φ(θ)是附加壓力隨管道傾角而變化的系數;θ為傾斜角度;CDr為阻力系數;k4為漿體處于滑、跳移狀態的固體顆粒占固體顆粒總重量的比例系數.當k4=0 時,漿體固體顆粒處于懸移狀態;當k4=1 時,漿體中固體顆粒處于滑、跳移狀態;當0 求得.公式(10)中的k3用公式 求得.其中,k' 是一個常數. 管內水力坡度i的公式[10]為 兩相流模型如圖1 所示. 圖1 兩相流的位能、壓能和動能 根據能量守恒定律,可推出該模型固液兩相流的伯努利方程[11]: 其中,H1-2=iL12cosθ;ρm為混合流體密度;L12為1,2 兩點間管道的距離;θ為管道傾斜角度;am1、am2為截面1 和截面2 上的動能修正系數;P1、P2為截面1 和截面2 對應的靜壓;Z1、Z2為截面1和截面2 對應的高度;vm1、vm2為截面1 和截面2 上的混合流體速度. 在漿體管道輸送中動能占總能量的比例很小,所以令am1≈am2≈1,所造成的誤差很小. 通過均質流界限速度的引入,來界定壓漿的速度,此時壓漿的漿體流動狀態處于偽均質流狀態,以此速度求得各段上下坡的水力坡度i,并設計壓漿時的始點壓力,即壓漿時預應力波紋管的進口壓力Ps. 其中,Ps為始點壓力;Sm為漿體的比重;ii為壓漿時各段管道的水力坡度;li為各段管道的長度;K1為附加系數();ΔH該段管道始端與末端的高差. 本試驗選用壓漿料最大粒徑長為185 μm,寬為120 μm.漿體運輸計算參數見表1. 表1 漿體輸送相關計算參數 本試驗選用潛水泵作為進行漿體輸送的動力裝置,外接2 m 長的塑料鋼絲軟管作為導管,將測試的不同管道外接在此軟管上,保證每次測量啟動水泵時的水位和軟管位置一致,試驗管道為10 m 長的PVC 管.通電待漿體從軟管口穩定流出后開始計時,在水位達到140 L 刻度時,停止計時并關閉電源,可得到穩定流速下灌滿140 L漿體所需要的時間,進一步計算得到出管速度的大小,重復試驗取均值,用以減小誤差.本驗證試驗以管徑及傾角為變量.試驗裝置見圖2. 圖2 不同管徑和傾角的試驗裝置 試驗過程中,對管道入口測得壓力P1,外接試驗管道即管徑50 和75 mm 的管道,分別測出各管道在各濃度下的出管壓力P2,從而求得壓力差ΔP,再與公式(16)的計算理論值相比較,結果見圖3. 由圖3 可知,在不同管徑、濃度、傾角情況下計算壓力差與理論壓力差大致相近,最大誤差為17%,最小誤差為1%,且一部分誤差來源于試驗器材的精度和測量時的誤差. 圖3 各試驗工況計算壓力差與試驗壓力差 在只考慮管道類型對漿體在管道運輸速度的影響試驗中,對比2 種不同管道所得到的漿體出管速度,從而得到預應力波紋管影響下漿體出管速度衰減系數值.試驗裝置見圖4. 圖4 不同類型管道漿體出管速度測定裝置 通過控制管徑(50 和75 mm)、濃度(0%,10%,20%和30%)等變量來進行對比試驗,試驗方法同驗證試驗.試驗結果見圖5. 圖5 預應力波紋管在不同條件下的出管速度 通過對比不同濃度的漿體在兩種管道輸送的出管速度,得到預應力波紋管影響下漿體出管速度衰減系數見表2. 表2 不同管徑、濃度條件下漿體出管速度衰減系數 由表2 可知,在不同漿體濃度和管徑的條件下,預應力波紋管中的漿體出管速度與光滑管壁中的漿體出管速度比值基本保持不變.為保證壓漿過程的通順性,選取較小的0.88 作為其出管速度衰減系數來進行計算,即 為探究預應力筋對漿體在管道中輸送速度的影響,在使用預應力波紋管的條件下,通過改變管內濃度以及預應力筋的數量,對比不同情況下的漿體出管速度,得到預應力筋對漿體輸送速度的影響關系,試驗結果見圖6,加入預應力筋條件下漿體速度衰減系數見表3. 圖6 添加預應力筋條件下的漿體出管速度 表3 加入預應力筋條件下漿體速度衰減系數 由表3 試驗數據可知,在50 mm 管徑的預應力波紋管中加入預應力筋,漿體速度衰減系數在不同漿體濃度的情況下基本保持不變,為保證壓漿過程順暢,因此選用濃度為0%時的速度衰減系數作為計算系數;對于75 mm 管徑的預應力波紋管,計算系數取摻入預應力筋條件下的漿體速度衰減系數平均值作為代表值.衰減系數與管內面積衰減系數對比見表4 及表5,摻入預應力筋的漿體速度衰減系數與管內面積衰減系數基本保持一致. 表4 摻入預應力筋條件下漿體速度衰減系數與管內面積衰減系數(50 mm 管徑) 表5 摻入預應力筋條件下漿體速度衰減系數與管內面積衰減系數(75 mm 管徑) 計算漿體輸送的均質流界限速度VH,再將均質流界限速度VH用試驗所得系數ζ1、ζ2進行修正,確定預應力管道壓漿時的均質流界限速度. 其中,ζ=ζ1*ζ2;ζ2為摻預應力筋時漿體速度衰減系數. 1)水力坡度驗證試驗中的計算壓力差與實測壓力差相近,且計算壓力大部分大于實測壓力差,對于壓力的適當增大更有利于漿體的輸送. 2)濃度、管徑、管壁的類別都會影響出管速度,管內濃度的增加或管徑減小會導致出管速度減小,其中導致出管速度減小的主要影響因素是管壁類別,其對應速度的衰減系數ζ1=0.88. 3)隨著預應力筋的加入,出管速度也會隨之減小,因速度衰減系數ζ2與管內面積衰減系數相近,使用管內面積衰減系數代替摻入預應力筋的漿體速度衰減系數ζ2,既可方便現場計算也更有利于壓漿的平順. 4)得到修正的均質流界限速度后,再通過修正公式及兩端高差來計算預應力管道壓漿施工過程中的壓漿壓力,并可使用此壓力作為壓漿過程中的最低壓力.


1.3 固液兩相流的伯努利方程

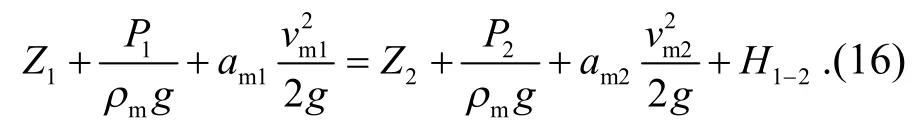
1.4 管道漿體輸送壓力

2 預應力管道壓漿的理論驗證及壓力修正
2.1 漿體輸送條件計算參數

2.2 水力坡度公式驗證試驗


2.3 預應力波紋管對均質流界限速度的影響研究
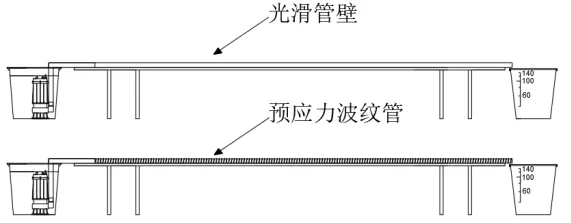



2.4 預應力筋對均質流界限速度的影響研究


3 結論

