考慮時空相關隨機行駛時間的車輛路徑問題模型與算法

張冬青， 郭釗俠， 張殷杰

(四川大學商學院， 成都 610065)

1 引 言

城市化加快了電子商務產業的發展，也催生了以及時、快捷、高效為目標的電商快遞、生鮮配送、冷鏈物流等行業. 在城市物流體系中，最后一公里配送是對接顧客的重要環節，其質量直接影響顧客的體驗和滿意度. 因此，如何制定最優的車輛配送方案和行駛路徑，高效地完成配送任務，一直是學術界研究的重要課題. 學術界通常將最后一公里配送問題建模為車輛路徑問題[1].

城市物流配送過程中存在著各種隨機因素. 根據所考慮的隨機元素的不同，隨機車輛路徑問題(Stochastic Vehicle Routing Problem, SVRP)主要可以分為考慮隨機顧客需求的車輛路徑問題[2]、考慮隨機顧客的車輛路徑問題[3]和考慮隨機時間(包含隨機的顧客服務時間、隨機的車輛行駛時間)的車輛路徑問題[4-5].

根據所考慮的道路網絡上車輛行駛時間是否具有時間依賴性，即車輛通過一條路段的時間是否會隨著從該路段端點出發時間的不同而發生改變，考慮隨機車輛行駛時間的SVRP又可以分為非時間依賴的SVRP[5]和時間依賴的SVRP[1]. 絕大多數考慮隨機車輛行駛時間的SVRP文獻都假設各路段的車輛行駛時間是服從于某種概率分布的獨立隨機變量，如正態分布、gamma分布和log-gamma分布等. 但是這些文獻并沒有考慮真實道路網絡中車輛行駛時間所存在的相關性.

基于真實的車輛行駛時間或速度數據，有學者[6-8]發現交通流在道路網絡上的演變會導致各路段的車輛行駛時間(或速度)之間存在時間和空間上的相關性(簡稱時空相關性)，即某一路段某一時段與另一時段另一路段的車輛行駛時間之間存在相關性. 雖然，道路網絡車輛行駛時間的時空相關性已經在隨機最短路徑問題[9]和交通預測[10]等領域中被廣泛考慮和研究，并且，Gendreau等[4]也指出考慮隨機量之間的相關性是SVRP未來重要的研究方向，然而，考慮隨機相關行駛時間的SVRP研究在國內還未見報道. 在國外，現有SVRP研究中考慮相關性的文獻也非常有限. Rostami等[11]研究了考慮隨機相關行駛時間的SVRP，以最大化行駛時間的可靠性為目標，提出了一種分支-定價-分割算法進行求解. Rajabi-Bahaabadi等[12]進一步考慮了軟時間窗約束，并以最小化車輛的行駛成本和違反時間窗的懲罰的總和為目標，提出一種最大-最小蟻群系統算法來求解. 然而，這兩篇文獻都沒有考慮真實的道路網絡和行駛時間的時間依賴性以及在時間維度上的相關性.Avraham和Raviv[13]進一步考慮了時間依賴的行駛時間和時空相關性，并研究了單個車輛的隨機相關SVRP，但是他們同樣沒有考慮真實的道路網絡.

基于真實道路網絡，本文考慮車輛行駛時間存在的時空相關性和時間依賴性，對相應的SVRP進行了研究. 該問題旨在將顧客所需要的產品分配到合適的車輛上，并安排每一輛車的行駛路線，來達到最小化司機加班費用與車輛CO2排放成本的總和的目標.

一方面，SVRP集成了整數規劃和隨機規劃的性質，是典型的NP-hard類組合優化問題. 因此，精確算法往往無法在合理的計算時間內進行求解，而啟發式方法和智能優化算法是廣泛應用于求解規模較大路徑優化和分配調度等問題的主流方法. 另一方面，隨機行駛時間之間的時空相關性會導致高維相關隨機量. 例如，一個包含1 000條路段和10個時間周期的道路網絡共有10 000個相關隨機量. 當處理如此高維度的相關隨機量時，傳統的蒙特卡洛仿真方法往往需要大量的場景才能反應出隨機變量之間的相關性[4]，進而導致過長的求解時間. 而基于copula的情景生成(Scenario Generation, SG)技術[14]已經被證明能以很少數量的場景有效地反映高維隨機變量之間的相關性[15]. 因此，本文旨在結合智能優化算法良好的尋優能力和SG技術處理高維相關隨機變量的優異性能，提出一類適用于不同規模SVRP的智能隨機優化方法，解決考慮時空相關隨機行駛時間的SVRP.

2.1 問題描述

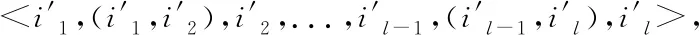
在目標函數中，本文綜合考慮了以司機加班成本為代表的經濟成本和以二氧化碳排放成本為代表的環境成本. 針對經濟成本，物流企業的運作中，除了人力成本，還存在油耗成本、維修成本、折舊成本等. 然而，由于汽車的油耗量與二氧化碳排放量近似成正比[16]，本文優化二氧化碳排放成本可以間接地降低油耗成本. 其次，車輛的維修成本和折舊成本受多種因素影響，如貨物的類別和司機的駕駛技術等，而難以在數學模型中準確地進行定量化表達. 因此，本文選取人力成本(司機加班成本)作為經濟成本的代表. 另一方面，針對環境成本，雖然汽車尾氣中包含二氧化碳、碳氫化合物、一氧化碳等多種氣體，但與二氧化碳排放量(對于輕型車，與油耗量的比值約為2.3 kg/L)相比，尾氣中的碳氫化合物和一氧化碳等氣體的排放水平很低(與油耗量的比值約0.01 kg/L)[16]. 并且，由于碳交易市場的建立，二氧化碳排放量可以直接轉化為企業的一項經濟成本來進行優化. 因此，本文選取二氧化碳排放成本來代表環境成本.

本文利用運輸排放和能源消耗計算方法(MEET)[17]來計算車輛行駛過程中CO2的排放量. 對于以速度v(單位： km/h)行駛的7.5～16 T的卡車，式(1)計算了其行駛單位距離的CO2排放量e(單位： g/km).

e=871-16v+0.143v2+32031/v2

(1)

2.2 數學模型

所研究的SVRP的兩階段隨機規劃模型如下式.

(2)

s. t.

(3)

(4)

(5)

(6)

(7)

(8)

2≤|S|≤n-1, k=1,...,K

(9)

xijk,yik∈{0,1},?i,j=0,...,n,i≠j,

k=1,...,V

(10)

對于每一個場景ξm：

(11)

[Lp,Up], m=1,...,M

(12)

(13)

sj, ?j=1,...,c,m=1,...,M

(14)

?j=c+1,...,n, (i′,j′)

∈E, m=1,...,M

(15)

(16)

?k=1,...,V, m=1,...,M

(17)

?m=1,...,M

(18)

m=1,...,M, (i′,j′)∈E

(19)

3 智能隨機優化方法

本文旨在針對考慮時空相關隨機行駛時間的SVRP提出一個高效的算法求解框架. 為了適用于現實中問題規模較大的SVRP，本文利用智能優化算法進行解的尋優，并創新性地將其與SG技術相結合，提出一種智能隨機優化方法. 該方法首先利用適用于車輛路徑問題的智能優化算法在解空間中搜索候選解；然后，利用SG技術產生的代表時空相關隨機行駛速度的場景集合對候選解進行評價. 混合粒子群優化(Hybrid Particle Swarm Optimization, HPSO)算法具有局部優化解與全局優化解相互結合的尋優機制，能夠成功地求解確定環境中的車輛路徑問題等離散優化問題. 因此，本文設計了一種HPSO算法來進行解的尋優. 在HPSO算法中，我們設計了一種貪婪的啟發式方法來得到真實道路網絡中兩個顧客點之間的具體行駛路徑；引入了可變鄰域下降算法來對粒子群優化算法搜尋到的解進行局部提升；并設計退火策略來更新自身最優解以避免陷入局部最優.

圖1 基于HPSO的智能隨機優化方法流程圖Fig.1 Flow chart of the HPSO-based intelligent stochastic optimization method

圖1展示了本文提出的基于HPSO的智能隨機優化方法的流程. 其中，我們首先利用SG技術產生能夠代表真實道路網絡中時空相關隨機速度的M個隨機場景；然后，利用HPSO算法搜尋解空間，找到候選解；再基于SG技術產生的隨機場景計算并返回給HPSO算法該候選解的適應度值，以幫助HPSO算法繼續搜尋解空間找到最優解. 算法的主要部分介紹如下.

3.1 隨機速度場景的產生

在隨機優化的框架下，首先我們使用基于copula的SG技術[16]產生能代表時空相關的隨機行駛速度的隨機場景集合. 在給定相同輸入數據的情況下，每次運行此SG技術會產生相同的隨機場景集. 因此，當所研究的時空道路網絡不發生改變時，隨機場景只需要產生一次. 利用SG技術產生隨機場景集的具體操作步驟如下.

Step1： 輸入所有隨機速度變量的邊際分布函數；

Step2： 輸入能代表隨機速度變量之間時空相關性的相關系數矩陣；

Step3： 使用基于copula的SG技術產生隨機場景集合ξ={ξ1,ξ2,...,ξM}，其中每個場景的發生概率為1/M.

3.2 粒子的編碼與解碼

本文采用沒有分隔符的所有顧客節點的序列來編碼所有粒子. 然后，利用傳統的隨機分割算子進行解碼，即將粒子隨機分割為與車輛數相等的V段. 如圖2所示，需要配送的10個顧客節點被依次劃分到3輛車上進行配送.

圖2 粒子表示方式Fig.2 Representation of a particle

3.3 種群初始化

為了更好地引導解的搜尋方向，我們首先利用最近鄰點啟發式方法得到一個初始粒子. 在這個啟發式方法中，車輛總會選擇距離當前節點最近的顧客點作為下一個配送目標，若配送下一個顧客點的貨物會導致車輛超載，則安排下一輛車從車場出發以下一個顧客點為第一個配送點繼續進行配送，直至所有顧客點的貨物全部配送完畢. 然后，種群中剩余的其他粒子均隨機產生.

3.4 粒子的評價

為了增強算法搜索的多樣性，本文允許非可行解以一定的懲罰費用進入尋優過程，并利用式(21)對候選解進行評價. 其中，F為SVRP的原始目標函數(式(2))的值；cl為對超載貨物的懲罰系數；OL為當前粒子超載的貨物量；t為算法迭代的次數.

Z=F+cl·OL·t

(21)

基于SG技術產生的隨機場景集ξ，分別對每一輛車的配送路線進行評價. 具體過程如下.

Step1： 令m=1；

Step2： 若m≤M，重復step3和step4，否則轉到step5；

Step3： 在場景ξm中，對所有相鄰的顧客點對(i,j)，利用3.2節所述方法計算顧客點i到顧客點j之間的行駛路徑，并根據式(12)計算hξm的值；

Step4： 置m←m+1；

Step5： 根據式(2)計算F的值，然后根據式(21)計算Z的值.

由于在隨機環境中對一個粒子進行評價需要計算其在M個場景下的適應度值，所以隨機問題中解的評價時間會比其對應確定問題中解的評價時間長很多. 為了節約計算時間，在用于全局搜索的粒子群優化算法中，我們使用M個場景對解進行評價，而在用于局部提升的可變鄰域下降算法中，我們僅使用一個確定場景. 在此確定場景中，各路段各時間周期的車輛行駛速度設置為相應隨機速度變量的均值.

3.5 粒子位置的更新

用于全局搜索的粒子群優化算法根據一定的執行概率利用三個作用于粒子的隨機變化操作，即突變、與自身最優解交叉和與種群最優解交叉，來更新粒子的位置. 具體使用的算子分別是swapmutation算子、erXover算子和erXover算子. swapmutation算子是經典的變異算子，即隨機選擇粒子中的兩個顧客點交換其位置；erXover算子基于所選父輩粒子中每一個節點的鄰居節點數量，通過循環地選出當前節點的相鄰節點中具有最少剩余鄰居節點數量的節點，來進行邊的重組以得到交叉后的粒子位置.

用于局部提升的可變鄰域下降算法依次使用三種路徑間變化算子crossover、swap(2, 2)和shift(1, 0)，以及兩種路徑內變化算子2-opt和relocate.對于以一定概率從種群中隨機選擇出的一個粒子，首先對其執行crossover算子，如果找到更好的解就更新當前粒子位置，并依次執行2-opt算子和relocate算子；如果沒有找到更好的解就按此規則依次執行路徑間變化算子swap(2, 2)算子和shift(1, 0)算子. 以此類推，直至執行完shift(1, 0)算子且沒有找到更好的解，則結束該可變鄰域下降算法，返回粒子的當前位置.

其中，路徑間變化算子crossover是隨機選擇分段點，將兩個父輩粒子都分割為前后兩部分，再將父輩粒子1的前一部分和父輩粒子2的后一部分組合成為改進的粒子，并將剩下的兩部分組合成為另一個改進的粒子.swap(2, 2)算子是從兩個父輩粒子中分別選擇兩個相連的節點片段，并交換這兩個所選片段的位置以組成改進的粒子.shift(1, 0)算子是將一個父輩粒子中的一個顧客節點插入另一個父輩粒子中，以得到改進的粒子. 路徑內變化算子2-opt算子先將當前粒子的兩條邊斷開，并組成另外兩條新的邊來代替斷開的邊，得到改進的粒子.relocate算子是將一個顧客節點從粒子中移除，再重新插入到當前粒子的其他相鄰節點之間以改進粒子性能.

3.6 更新自身最優解和種群最優解

每次迭代后，檢查是否達到了給定算法的最大迭代次數或達到種群最優解連續未更新的最大迭代次數. 如果滿足任一條件，算法運行終止，返回種群最優解作為此智能隨機優化方法找到的最佳解.

4 數值實驗

4.1 算例描述

為了驗證設計的智能隨機優化方法的有效性，本文基于Augerat等[18]提出的帶有裝載限制的車輛路徑問題算例A-n36-k5，構建了車場和顧客數量的總和分別為19、27和36的三個算例集. 這3個算例集的顧客需求分別為A-n36-k5中前19、27和36個顧客的需求，其中第一個節點為需求等于0的車場. 車場中可利用的車輛數分別為3、4、5，且每輛車的最大載重與算例A-n36-k5中的設置一致. 所有測試算例均定義在包含327個節點和1 207條邊的北京市區道路網絡上. 在每一個算例集中，利用Huang等[1]使用的方法得到顧客隨機分布(R)、集中分布(C)、一部分隨機分布另一部分集中分布(RC)的3個算例.圖3展示了在簡化的北京道路網絡中算例R36的顧客分布情況.

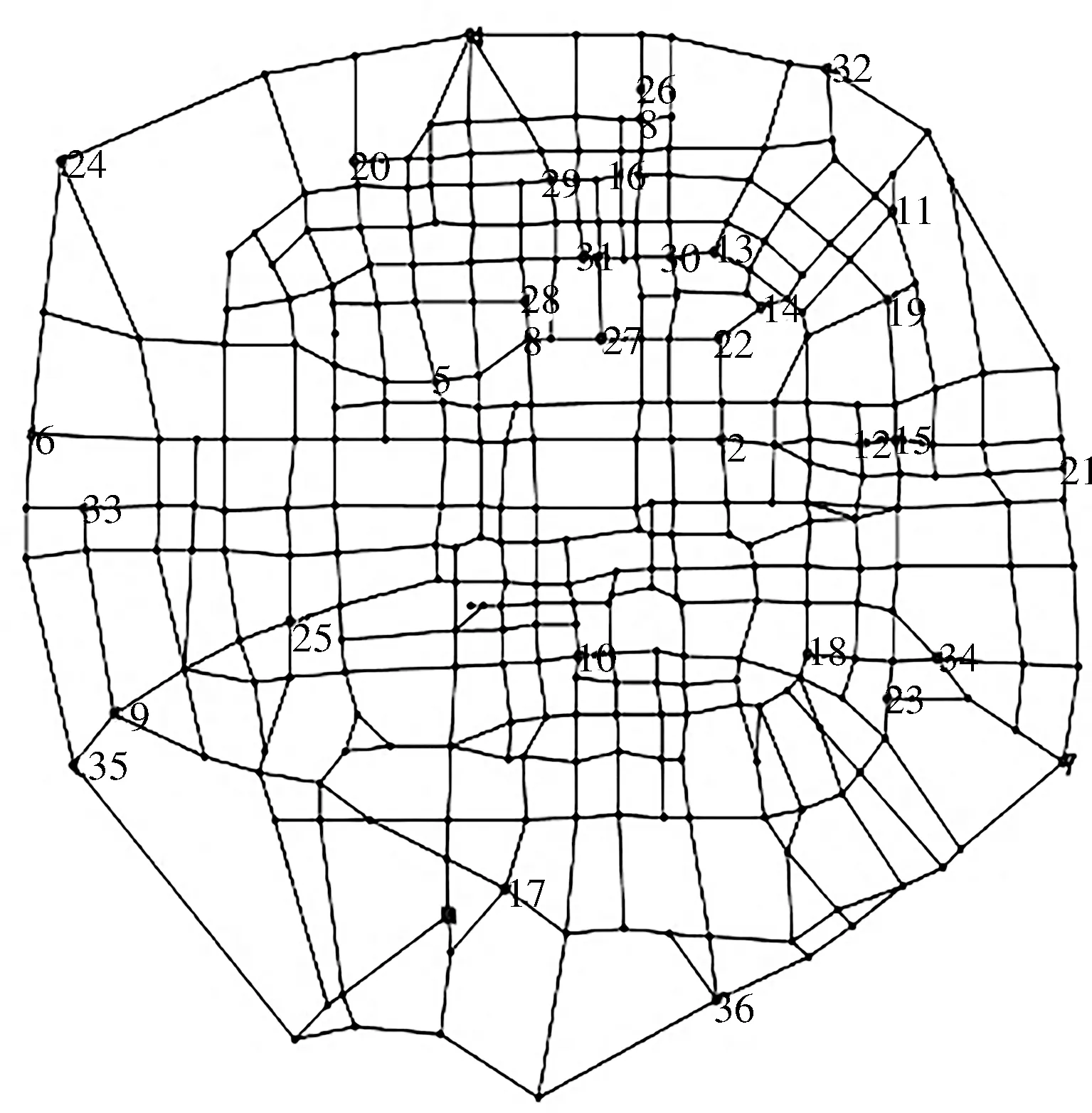
圖3 算例R36的顧客分布

司機的單位時間加班費用c1設置為25元/h. 根據報告[19]，單位CO2排放成本c2設置為248.15元/噸. 以早班為例，設定車輛在早上8∶30離開車場，中午12∶00返回，則司機的工作時長WT為3.5 h. 每位顧客的服務時間設為20 min. 道路交通情況變化的時間周期設置為30 min，則整個計劃期有8個時間周期(如表1所示). 因此，本文需要處理含有9 656(1 207×8)個相關隨機量的時空網絡.

與文獻[15]一致，本文設定每條路段每個時間周期的車輛行駛速度服從有界beta分布.其中,參數α和β等于Dmax/(l·Kp)，Dmax表示道路網絡中距離最長的路段長度，l為當前路段的長度，Kp為當前時間周期道路擁堵程度的常數，且Kp越小代表道路越擁堵. 每一個時間周期道路網絡的Kp值、最大、最小和平均的車輛行駛速度如表1所示. 為了表示道路網絡行駛時間的時空相關性，本文設定兩個連續時間周期之間的時間相關系數為0.4；兩個相鄰路段之間的空間相關系數為0.4；相鄰路段在相鄰時間周期的時空相關系數為其時間相關系數與空間相關系數的乘積；其他情況下的相關系數為0. 利用樣本內外測試方法，發現對于所構建的測試算例，10個隨機場景即可保證對解評價誤差在2%以內，因此本文設定隨機場景數量M為10.

通過多次實驗比較，設定智能隨機優化方法的參數如下：種群中的粒子總數為20，超載貨物的懲罰系數cl為0.5，用于更新粒子位置的swapmutation算子的執行概率為0.2，erXover算子的執行概率為0.6，執行可變鄰域下降算法時從種群中選擇粒子的概率為0.3，更新自身最優解時的初始溫度T(0)為30，程序的最大迭代次數為500，種群最優解連續未更新的最大迭代次數為100. 所有程序使用MATLAB R2016b編寫，程序運行環境為Inter Core i5-6200U CPU @ 2.30 GHz和12 GB RAM的筆記本電腦.

表1 各時間周期速度分布的設定

4.2 實驗結果

4.2.1 算法比較 為了檢驗設計的HPSO算法的求解性能，本文將其與單純的粒子群優化算法和混合遺傳算法進行對比. 其中，提出的HPSO算法中若不使用用于局部提升的可變鄰域下降算法，即為粒子群優化算法；傳統的遺傳算法結合上述可變鄰域下降算法，即構成混合遺傳算法.其中所用到的選擇算子為錦標賽選擇算子，交叉和變異算子分別為erXover算子和swapmutation算子. 所有算法運行10次，結果的平均值如表2所示. 由于對于同一個時空網絡，利用SG技術產生的隨機場景可以重復使用，表格中的程序運行時間不包含產生隨機場景的時間.

表2中的結果表明,混合粒子群優化算法在求解質量和計算效率上均具有一定的優勢. 雖然，粒子群優化算法所用時間很短，但由于沒有對解進行局部提升，其求解性能明顯差于另外兩種混合算法. 混合粒子群優化算法和混合遺傳算法的求解時間差異不大，但是很明顯，對于所有算例，混合粒子群算法的求解性能總是更優.

4.2.2 時空相關性分析 為了進一步分析在SVRP中考慮道路網絡車輛行駛時間的相關性的意義，本文以算例R27為例比較了不同的時間和空間相關系數組合下的求解結果. 取10次運行的最佳解，結果如表3所示. 在相關系數不同的隨機場景中，同一個解的評價值會存在差異；為了研究不同相關系數組合對解的影響，本文利用時間和空間相關系數均為0.4的隨機場景重新計算了所有解的目標值，并將其作為比較基準值.

表3中的結果表明，考慮與不考慮時空相關性所得到的解會存在一定差異；考慮不同的時間和空間相關系數組合往往會得到不同的解，進而導致不同的總成本；并且，若考慮的時間和空間相關系數與實際情況不符，往往會得到在實際中表現更差的解. 因此，準確地考慮真實道路網絡中車輛行駛時間所存在的時空相關性才能得到適用于實際交通環境的最優路徑決策方案.

本文進一步分析了不同空間和時間相關系數分別對各項成本的影響. 圖4展示了時間相關系數(或空間相關系數)為0.4時，不同空間相關系數(或時間相關系數)下各項成本的數值. 由圖4可以看出，總成本的波動主要來源于加班費用的波動，這說明相比于CO2排放成本，司機加班時間(費用)受不同空間和時間相關系數的影響較大. 因此，考慮道路網絡車輛行駛時間的時空相關性對企業減少司機的加班時間和提高物流配送效率有重要的現實意義.

表2 不同算法結果比較

表3 不同時空相關系數組合下的總成本(單位：元)

本文以真實的城市道路網絡為背景，以最小化司機加班費用和車輛CO2排放成本的總和為目標，研究了考慮時空相關的隨機行駛時間的車輛路徑問題. 首先，建立了該問題的兩階段隨機規劃模型. 然后，結合智能優化和隨機優化技術，提出了一種智能隨機優化方法. 該方法利用一種結合了可變鄰域下降算法的HPSO算法進行解的尋優，并利用基于copula的SG技術產生隨機場景來對候選解進行評價.

基于北京市區道路網絡，本文進行了一系列的數值實驗. 實驗結果驗證了所提出的智能隨機優化方法的有效性. 同時，結果表明對于所研究的問題，提出的混合粒子群優化算法的尋優性能優于混合遺傳算法以及傳統的粒子群優化算法；考慮真實道路網絡中車輛行駛時間之間的時空相關性能夠得到更加符合實際交通環境需求的車輛路徑方案，從而幫助企業在綜合考慮經濟和環境成本的情況下做出更高效的車輛路徑決策.

本文的數值實驗是基于假設的時空相關車輛行駛速度數據，未來的研究將通過獲取真實的交通數據來進行實證研究. 另一方面，近年來，一些精確算法被提出求解具有特定特征的VRP. 未來的研究可以在本文提出的算法框架下，利用這些精確算法替換本文用于尋優的HPSO算法，來求解考慮時空相關的隨機行駛時間的SVRP，并對比研究其與本文提出的智能隨機優化方法的性能差異以及各自的適用場景. 未來的研究還可以集中在考慮更多的實際應用場景，比如多個優化目標、異質型的車輛、顧客服務時間窗的限制等.