線性調頻相參脈沖雷達信號模糊函數仿真分析

郭徽東

(解放軍92403部隊，福建 福州 350007)

0 引 言

相參脈沖串信號是現有雷達信號中應用最廣的一種。相參脈沖線性調頻雷達具有時頻耦合性和“釘板”型模糊圖，在距離、速度上同時具有良好分辨率和測量精度[1]。從雷達信號模糊函數的角度，仿真分析了相參體制下大時寬大帶寬脈沖線性調頻雷達信號距離/速度分辨率、低截獲和抗干擾特點。

1 模糊函數

模糊函數作為重要的信號時頻分析工具，具有唯一性、原點對稱性和體積不變性等特性[2-3]。根據模糊函數的性質，利用固定載頻矩形脈沖信號的特點，計算線性調頻矩形脈沖信號模糊函數，即:

χu(τ;fd)=

(1)

|χu(τ;fd)|2=

|τ′|≤τ

(2)

如果雷達接收到的點目標回波信號表示為：

(3)

式中：Xμ(τ;fd)為模糊函數,τ為時延,fd為多普勒頻移；τ′為矩形脈沖寬度；t為時間;μ為瞬時頻率的變化斜率。

2 雷達信號與仿真

2.1 雷達信號

現有雷達通常采用相參脈沖處理技術，脈內為線性調頻體制。選用2個相參雷達脈沖信號仿真模擬，進行載頻固定。其中，信號樣式A的重復周期為3 000 μs，脈寬50 μs，帶寬2～5 MHz；信號樣式B的重復周期為2 000 μs，脈寬180 μs，帶寬150～200 MHz。雷達脈內參數如表1所示。根據模糊函數理論性質，在仿真計算中采用相參線性調頻波形方式比較兩類信號模糊函數值，為減少計算量，假設1組脈沖序列數為5～20個。

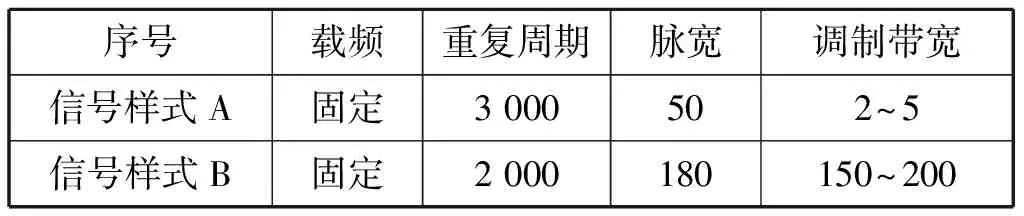
表1 仿真雷達信號參數

2.2 模糊函數計算

信號樣式A:重復周期3 000 μs，脈寬50 μs，帶寬2～5 MHz。當信號樣式A的脈沖個數N=5時，相參線性調頻信號的模糊函數計算結果見圖1，雷達主瓣寬度在時延軸上的投影對應雷達的距離分辨力；主瓣寬度在頻移軸上的投影對應雷達的多普勒速度分辨力。當信號樣式A的脈沖個數N=10時，數值計算結果見圖2～圖4；圖3(a)、(c)為相參線性調頻-時間模糊切片圖(N=10)，圖3(b)、(d)為相參線性調頻-速度模糊切片圖(N=10)。可以看出，雷達信號樣式A的相參脈沖信號周期重復特性使得模糊函數投影平面出現尖峰排列，模糊帶包絡寬度為1/τ，寬度與單脈沖一致，距離模糊瓣數目為時延與脈寬比。由圖3的速度模糊圖可以看出，速度模糊瓣間隔為1/T，寬度為N倍間隔，速度分辨率計算與圖中的主瓣尖峰寬度基本符合。由圖1和圖2可知，該信號樣式模糊函數尖峰不明顯，距離和速度上旁瓣現象明顯，旁瓣高度約為模糊瓣高度的1/N。此外，從二維平面投影看，速度和距離分辨率較低，信號響應區與雜波區分離度差。圖4為副瓣電平圖。旁瓣歸一化電平(-25 dB～-35 dB)能夠提供一定的距離和速度分辨率，對截獲接收機匹配截獲處理能力較弱。比較圖1、圖2，脈沖個數增加后，時域頻域切面的尖峰分離，主副瓣比提高，但總體上模糊函數釘板不明顯，模糊性大。

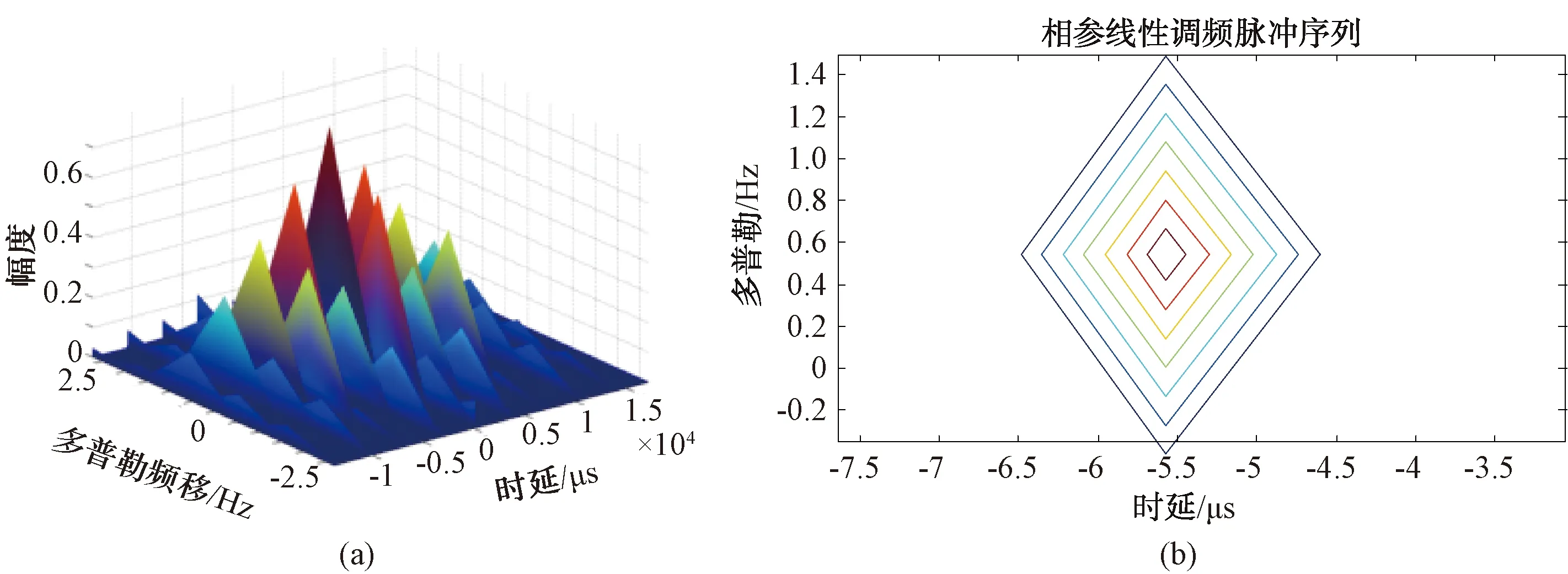
圖1 相參線性調頻脈沖序列模糊函數及投影圖(N=5)

圖2 相參線性調頻脈沖序列模糊函數及投影圖(N=10)

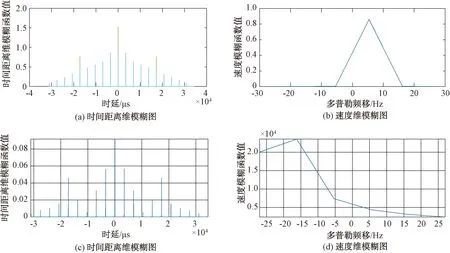
圖3 時間與速度模糊切片(N=10)

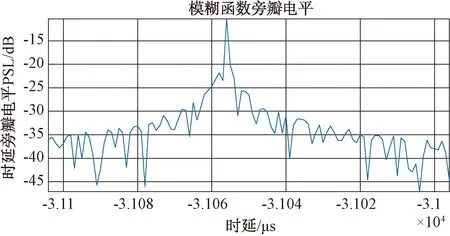
圖4 模糊函數旁瓣歸一化電平

信號樣式B：重復周期2 000 μs，脈寬180 μs，帶寬150～200 MHz，脈沖個數N=3、N=10。圖5、圖7分別為雷達信號樣式B單脈沖N=3和N=10時相參線性調頻脈沖序列線性調頻-模糊函數三維圖，圖7說明單脈沖模糊函數尖峰明顯，時頻域耦合性較信號樣式A弱，單脈沖模糊函數投影圖顯示線性調頻斜率的刀刃現象不明顯；在N=3和N=10的三維圖中，時域尖峰圖釘非常明顯，峰值幅度約為20～30，模糊函數在最大值的尖銳度大。理論上，距離模糊函數的主峰越窄，對相鄰目標分辨能力就越強。雷達信號樣式B帶寬200 MHz，具有大壓縮比大調頻帶寬，其時間軸上脈沖寬度變窄，距離切片中分辨率得以提高，主瓣寬度2～3 μs；圖8中的線性調頻-速度模糊切片的速度域主瓣寬度為1～2 Hz,脈沖數的變化與分辨率無關，與信號帶寬有關。圖9為模糊函數時延旁瓣電平，最低副瓣電平為-40～-190 dB，說明帶寬越大，旁瓣電平越低。信號樣式A和B的性能比較見表2。

表2 信號樣式性能比較

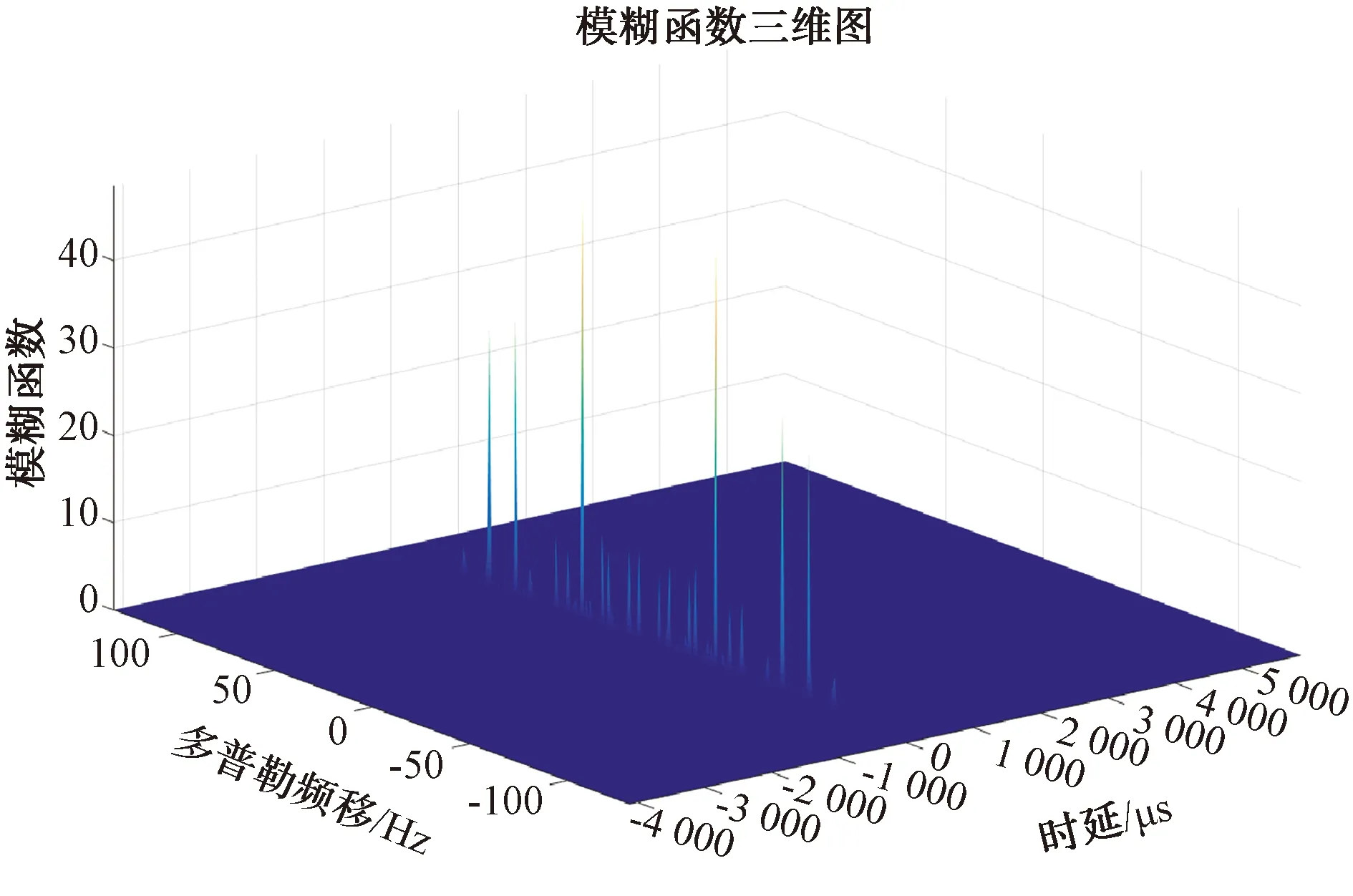
圖5 樣式B脈沖數相參線性調頻-模糊函數圖(N=3)

由圖1、圖2、圖6、圖8可知，脈沖線性調頻雷達信號τ-fd平面上呈現排列模糊釘板尖峰；時間距離τ=0模糊切片決定距離分辨率，fd=0速度模糊切片決定速度分辨率力，且信號模糊尖峰尖銳度、邊峰和主峰容積與空白區決定了雜波分辨能力和目標區分響應。總體上，信號樣式A的時頻耦合性強，具有較明顯的線性調頻特點，模糊主瓣寬，分辨率低，旁瓣多，副瓣現象較嚴重，且模糊函數釘板不明顯，尖峰幅值為0.4～0.6；信號樣式B脈沖個數增加后，峰值陡峭，圖釘明顯，幅度稍增加，脈沖序列的時域展寬大，τ-fd軸上單個脈沖信號分辨能力強，理論上具有較高的低截獲特性。

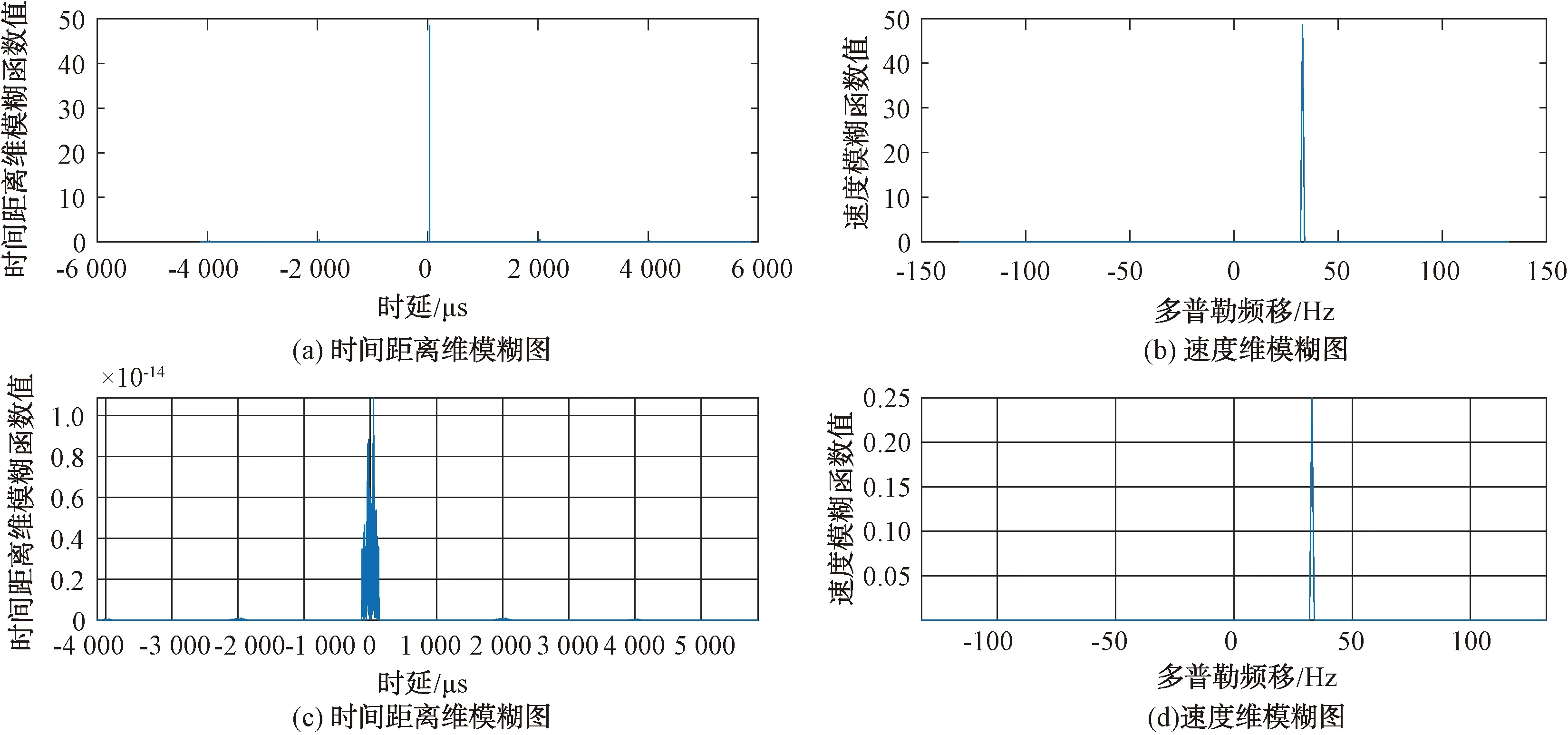
圖6 樣式B時間模糊切片與速度模糊切片(N=3)

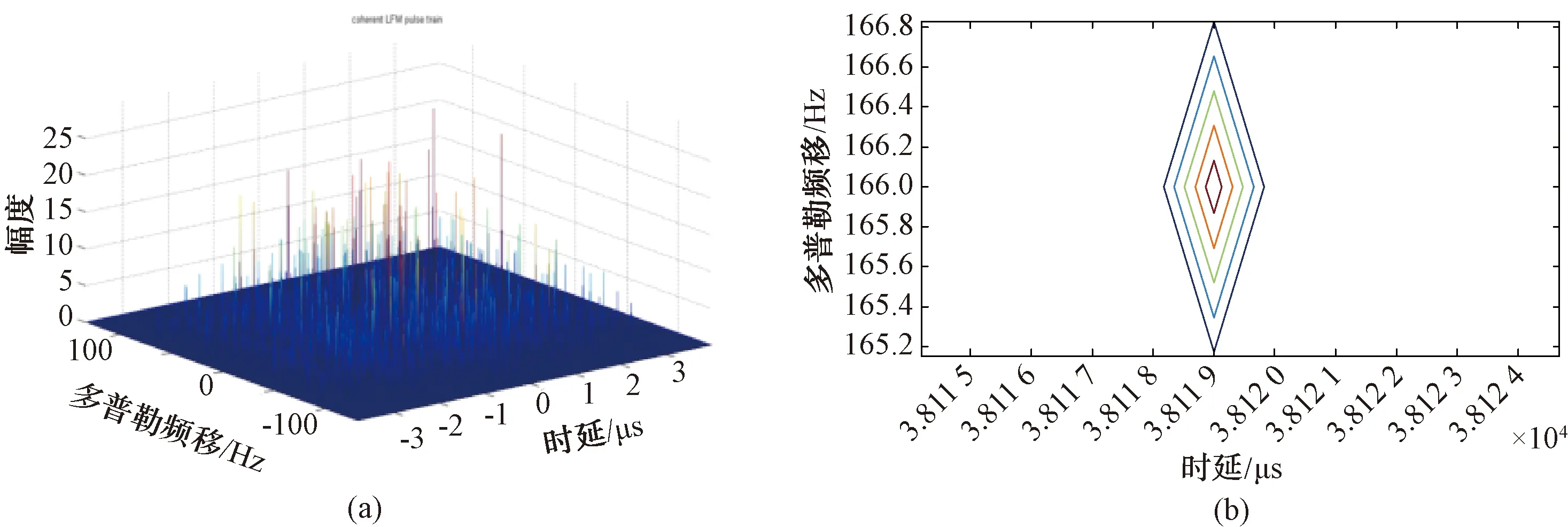
圖7 相參線性調頻雷達脈沖序列三維模糊函數圖平面投影圖(N=10)

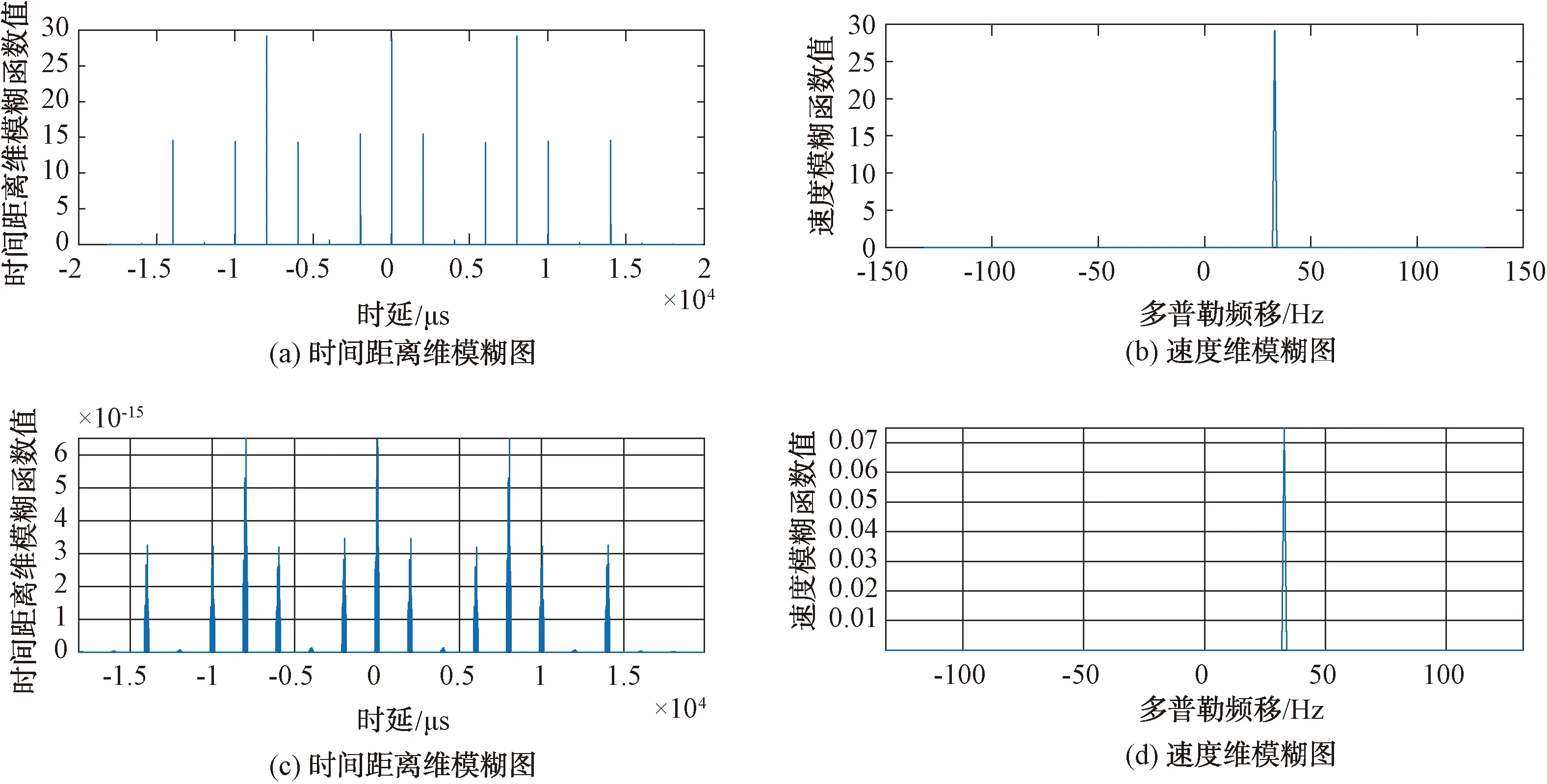
圖8 脈沖數相參線性調頻-時間模糊切片與時間模糊切片放大圖(N=10)

圖9 模糊函數旁瓣歸一化電平

3 結束語

通過不同信號樣式的仿真計算，受脈沖序列和波形不連續等影響，脈沖體制雷達均存在距離和速度模糊的可能，可采取重頻參差、滑變和抖動等方式來解決多值性、模糊問題，如附加其他調制，可改變模糊函數的形式，使之趨于圖釘型。