基于多值關聯規則的編隊作戰案例調整方法研究

孟慶林，陳 健，毛建舟

(海軍大連艦艇學院，遼寧 大連 116018)

0 引 言

目前，案例推理技術已經逐步應用于艦艇編隊作戰決策系統設計，它能夠很好地處理海上作戰指揮過程中的不良結構決策問題，為艦艇編隊作戰決策提供了新思路。但是，將歷史案例直接應用于決策問題時還存在不適宜的情況，如何將案例檢索中相似度不高的案例調整為適合當前態勢的決策是案例調整的關鍵。目前，案例調整的主要方法分為3種：(1)基于統計型的調整方法[1]，存在調整能力有限，誤差過大的問題；(2)案例推理和規則推理相結合的調整方法[2-3]，大量規則由領域專家制定，存在不夠客觀、規則庫龐大等問題；(3)基于機器學習的調整方法[4-6]，樣本需求大、計算量大，且僅能處理數值型數據。鑒于海上編隊作戰決策具有態勢屬性多、數據類型豐富的特點，使用以上方法不能很好地解決編隊作戰案例的調整問題。

本文運用數據挖掘中多值關聯規則算法挖掘作戰案例中的潛在知識，建立相應的關聯規則庫，根據編隊作戰特點制定消解沖突規則的方法，解決了案例調整時的規則沖突問題，避免了領域專家設置決策規則偏主觀、工程量大的問題，也彌補了機器學習類方法僅能調整數值型數據的局限。通過仿真實驗，證明該方法是有效的。

1 編隊作戰案例表示

案例表示是案例推理的基礎，編隊作戰案例形式如表1所示，{C1,C2,…,Ch}為歷史案例庫，Co為目標案例，也即待決策的問題；P={P1,P2,…,Pn}，為編隊作戰案例的態勢屬性；S={S1,S2,…,Sm}為編隊作戰案例的決策屬性。Ci={P,S}={xi1,xi2,…,xin;yi1,yi2,…,yim}表示某一個完整的作戰案例，xin為第i個案例中第n個態勢屬性，yim為第i個案例中第m個決策屬性，xin、yim可以是具體屬性值也可以是具體屬性的分類。態勢屬性主要為艦艇類型、艦艇數量、編隊類型，決策屬性主要為編隊前出接敵的展開方式、攻擊目標、編隊發射導彈數量等。

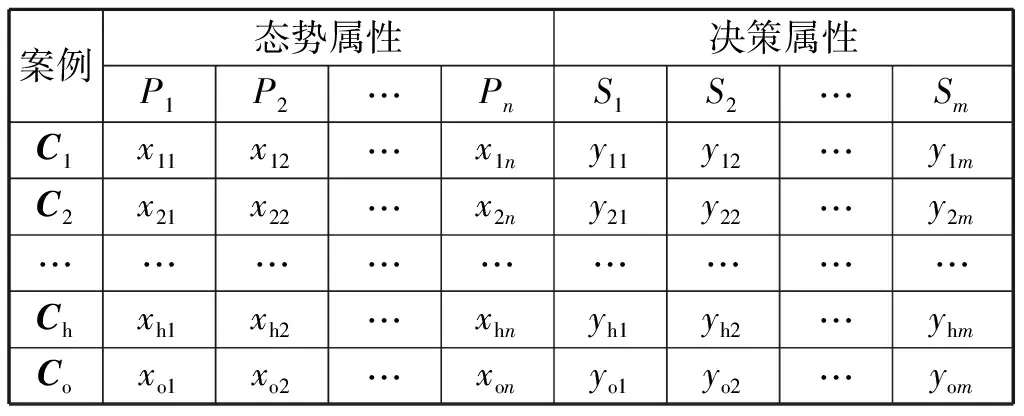
表1 編隊作戰案例

2 多值關聯規則算法挖掘編隊作戰案例的潛在知識

關聯規則是數據挖掘中的經典算法，它能很好地發現數據之間的潛在關系。如果能挖掘編隊作戰案例中態勢屬性和決策屬性之間的關系，就能利用挖掘的知識為編隊作戰決策提供依據，同時也可用于調整編隊作戰案例。

2.1 關聯規則的基本模型

R.Agrawal提出關聯規則并創立了經典的Apriori算法[7]，為數據挖掘奠定了理論基礎。

關聯規則的核心是從大量非相關數據中挖掘數據中的潛在知識，它是逐步掃描滿足支持度和置信度閾值的迭代算法。其主要分為2步：(1)通過掃描、計算、產生頻繁項集、連接及剪枝等步驟產生候選項集，進而尋找所需的頻繁項集，重復上述步驟，直到不能產生更大的頻繁項集為止；(2)產生關聯規則結果，對于每個頻繁項集，計算其置信度，輸出大于最小置信度閾值的關聯規則。

關聯規則的邏輯形式為X?Y。

支持度為屬性X在數據庫中出現的頻率：

Dsupport(X)=P(X)

(1)

置信度(信任度)為屬性Y在屬性X的條件下出現的頻率：

(2)

提升度用于判斷挖掘的規則是否有用，大于1時，認為關聯規則X?Y可信度較高：

(3)

2.2 改進的多值關聯規則

多值關聯規則(Q-Apriori)是在Apriori算法上的延伸，由于Apriori算法主要用于挖掘布爾型關聯規則[8]，對于數據集中每種屬性含有不同數值時，Apriori算法則無法處理，一般會將多值數據轉換為布爾型數據，再使用Apriori算法。在編隊作戰案例中，每種態勢屬性可能有不同的值，顯然是多值數據，如果將多值數據轉換為布爾型數據，勢必會導致頻繁項集的數量呈指數增加，進而加大計算量。因此，重點是將多值關聯規則改進為適合編隊作戰的案例。

在編隊作戰案例中，多值數據存在明顯的從屬關系、因果關系，并且絕大多數屬性值不大于5、分類屬性可列舉且不大于10，例如編隊中同種軍艦的數量、編隊的類型。基于上述特點，無需將多值數據轉換為布爾型數據，而是在Apriori算法的基礎上，通過優化確定頻繁項集的剪枝環節，減少大量非必要的運算，實現挖掘多值數據之間的關聯規則。

在挖掘關聯規則時，會形成大量頻繁項集，由于相同屬性的不同數值構成的頻繁項集無意義、只含有條件屬性或者決策屬性的頻繁項集也無意義，所以在剪枝環節中刪除上述可能的候選頻繁項集，減少生成頻繁項集的數量，避免無用的運算。例如候選頻繁項集：{驅逐艦-2，驅逐艦-1，導彈發射-8}，因同一候選頻繁項集中，同種屬性包含了不同值，在案例中不可能存在，它是支持度為0的無效候選集，應刪除。

此外，由于導彈發射數量比較離散，不利于挖掘{態勢屬性}?{導彈發射數量}的關聯規則，因此，需將導彈發射數量(決策屬性)進行等距轉換，從而挖掘到更加全面的關聯規則。等距轉換公式為：

(4)

改進的多值關聯規則算法流程如圖1所示。

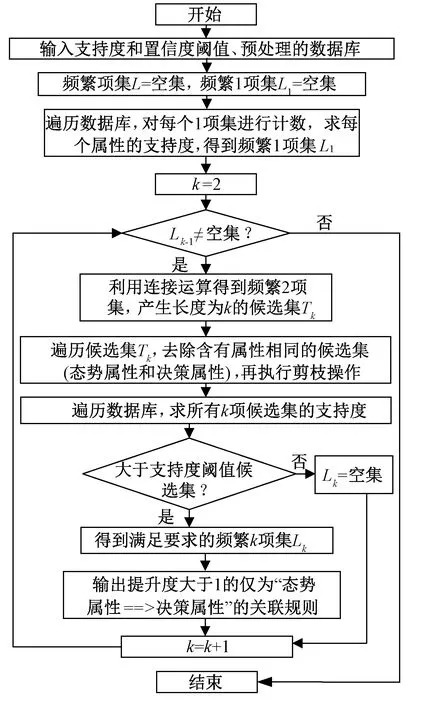
圖1 多值關聯規則流程圖

3 編隊作戰案例的調整方法

編隊作戰案例調整分為3步，如圖2所示。(1)編隊作戰案例庫中挖掘關聯規則(第2節)，建立相應的規則庫；(2)依據當前態勢，檢索案例庫，得到最相似的案例，判斷相似度是否大于閾值，大于閾值時，直接使用檢索的案例作為當前態勢的解決方案；小于閾值時，進入案例調整階段；(3)依據當前態勢遍歷已挖掘的規則庫，將與當前態勢相匹配的規則用以調整案例，當匹配的規則存在沖突時，根據編隊作戰特點制定相應的消解方法，從而解決了規則沖突問題，保障案例調整的可靠性。關聯規則對案例的調整原則：和當前態勢相匹配的規則生成相應的決策，將該決策替換原案例中相應的決策，對原案例中未調整的部分保留。

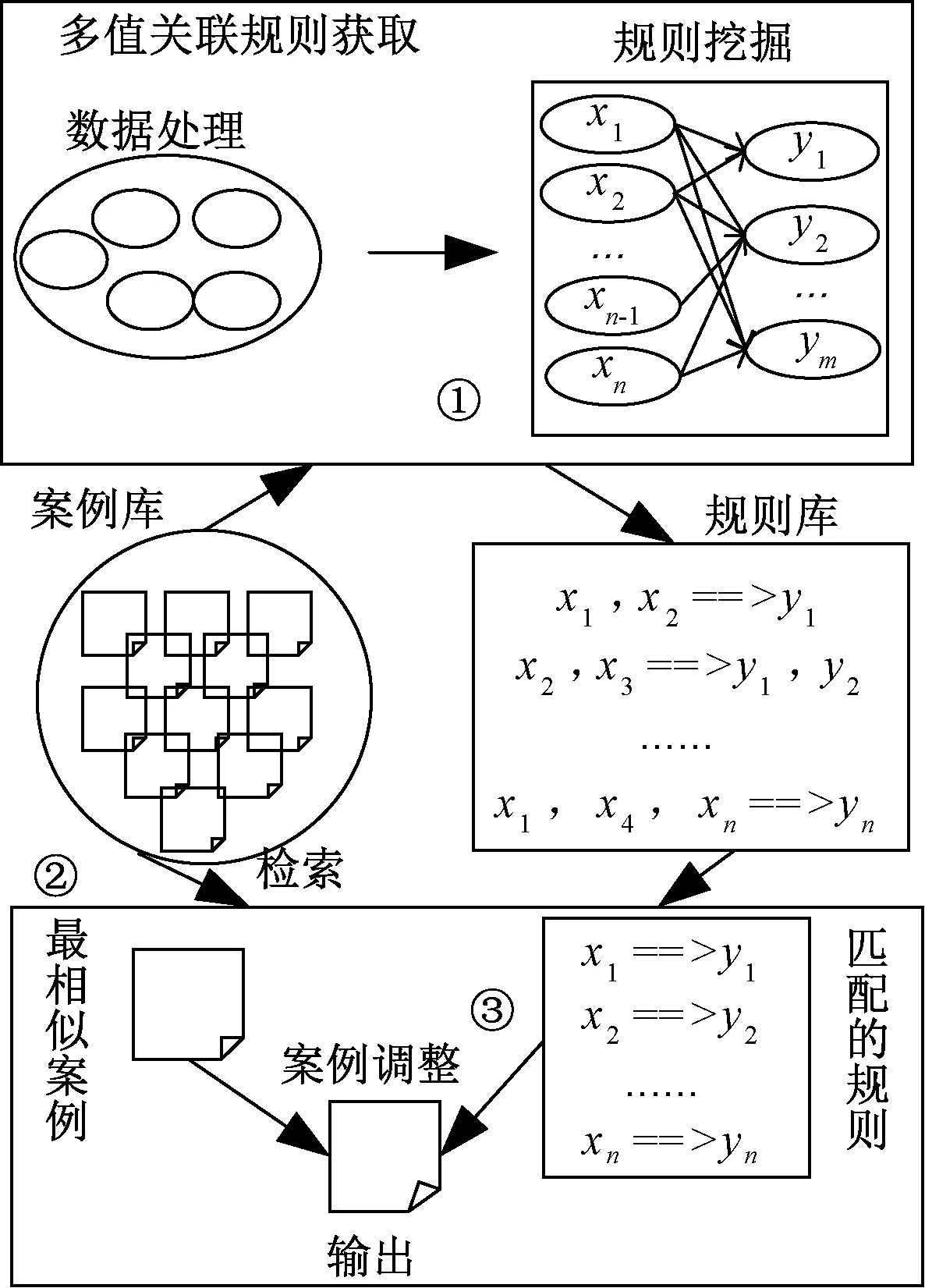
圖2 案例調整過程

3.1 獲取最相似案例

基于案例推理的編隊作戰決策，首先就是案例檢索，案例檢索的閾值為0.9，保證能夠檢索到足夠相似的案例，單個屬性的相似度計算公式為：

(5)

式中：xhi為第h個案例中的i個屬性值;xoi為當前態勢的i個屬性值。

全局相似度計算公式為:

(6)

式中：Ch,Co分別表示歷史案例和目標案例；wi為對應特征屬性的權重，和為1；Ds(Ch,Co)為全局相似度，值越大，案例相似度越高。

3.2 沖突關聯規則的消解

在利用挖掘的關聯規則制定決策時，關聯規則之間可能存在沖突，使得無法制定有效的決策。為了保障決策的可靠性，需要進一步消解規則之間的沖突。

3.2.1 關聯規則沖突情況

同種決策屬性存在決策的具體值不同的情況，這就造成了規則沖突，例如:

規則1表示決策屬性D1屬性值為1，規則2表示決策屬性D1屬性值為2。當條件同時滿足規則1和規則2時，結果卻產生了沖突。為了保證決策的可靠性，制定了符合編隊作戰決策的沖突規則消解方法。

3.2.2 沖突關聯規則的具體解決方法

在海上編隊作戰時，遵守一個戰斗原則：集中核心力量消滅敵方核心兵力部署。此外，研究發現我方兵力與兵力展開類型呈正相關，敵方兵力與我方決定的攻擊目標和導彈發射數量呈正相關。基于上述2點原因，現做出消解沖突規則的方法。

方法1：關聯規則的優先級與規則中態勢屬性的作戰力量優先級相對應(海上作戰力量的排序：航母>驅逐艦>護衛艦>導彈艇>作戰支援艦)。例如存在A1>A2>A3的優先級順序，則3.2.1小節中的沖突規則就可以確定使用規則1，棄用規則2。

方法2：用含我方兵力態勢屬性的規則推導我方兵力展開類型，用含敵方兵力態勢屬性的規則推導發射導彈數量和攻擊目標，并且是多屬性推導單個決策。

4 仿真實驗

本文選取了35個編隊作戰案例，其中30個案例用于挖掘關聯規則，另5個用于測試案例調整的精度。如表2所示，其中字母表示態勢屬性，數值表示相應屬性的數量或屬性的類型。

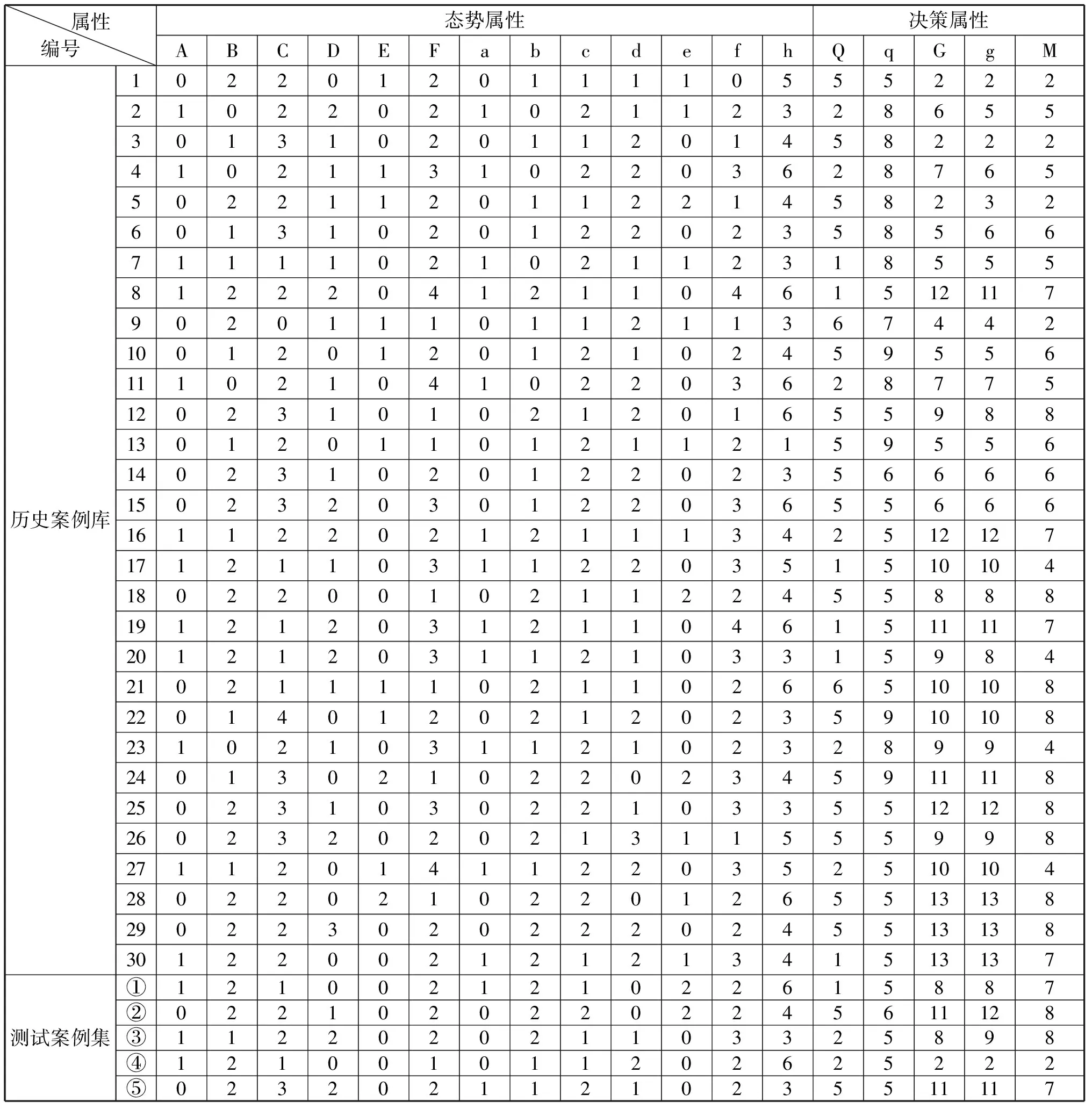
表2 艦艇編隊作戰案例

我方兵力：A：航母，B：驅逐艦，C：護衛艦，D：導彈艇，E：作戰支援艦，F：直升機。

敵方兵力：a：航母，b：驅逐艦，c：護衛艦，d：導彈艇，e：作戰支援艦，f：直升機，h：編隊類型。

艦艇編隊類型可分為單橫隊、單縱隊、V字隊形、左右梯形、交錯隊形、楔形隊形，表中分別用1、2、3、4、5、6表示。

決策屬性：Q：集群1，q：集群2，G：集群1導彈攻擊，g：集群2導彈攻擊，M：攻擊目標。

編隊在海上對敵攻擊時，一般分為2個集群兵力展開。可以按照1：航-驅(航母-驅逐艦為主的集群兵力展開)、2：航-護、3：航-導、4：航-作、5：驅-護、6：驅-導、7：驅-作、8：護-導、9：護-作、10：導-作為主的集群進行兵力展開。

攻擊目標通常選擇敵方核心力量，這里用相應的數字代替，1：航母，2：驅逐艦，3：護衛艦，4：航-驅(航母和驅逐艦)，5：航-護，6：驅-護，7：航-驅-護，8：驅-驅，9：護-護。

對海武器：YJ-18反艦導彈和YJ-83反艦導彈，每個集群的載彈量肯定能支撐一場戰斗。對海攻擊采用飽和式打擊方式，只需1枚導彈命中目標，對目標也能造成毀滅性的打擊。

4.1 編隊作戰案例調整

為了從案例庫中挖掘相對全面的規則，經過反復實驗后，將Q-Apriori程序中的最小支持度設置為0.133(4/30)、最小置信度為0.5，得到的關聯規則效果最好。

為了使讀者更好地明白本文案例調整的原理，本文給出了測試案例③的調整過程和結果。

通過案例檢索得到最相似的案例為16，相似度僅為0.835 2，低于相似度閾值0.9，所以歷史案例16的作戰方案不能直接使用，需要對作戰方案進行調整。

用測試案例③的態勢屬性遍歷規則庫，可以得到如表3所示的關聯規則。

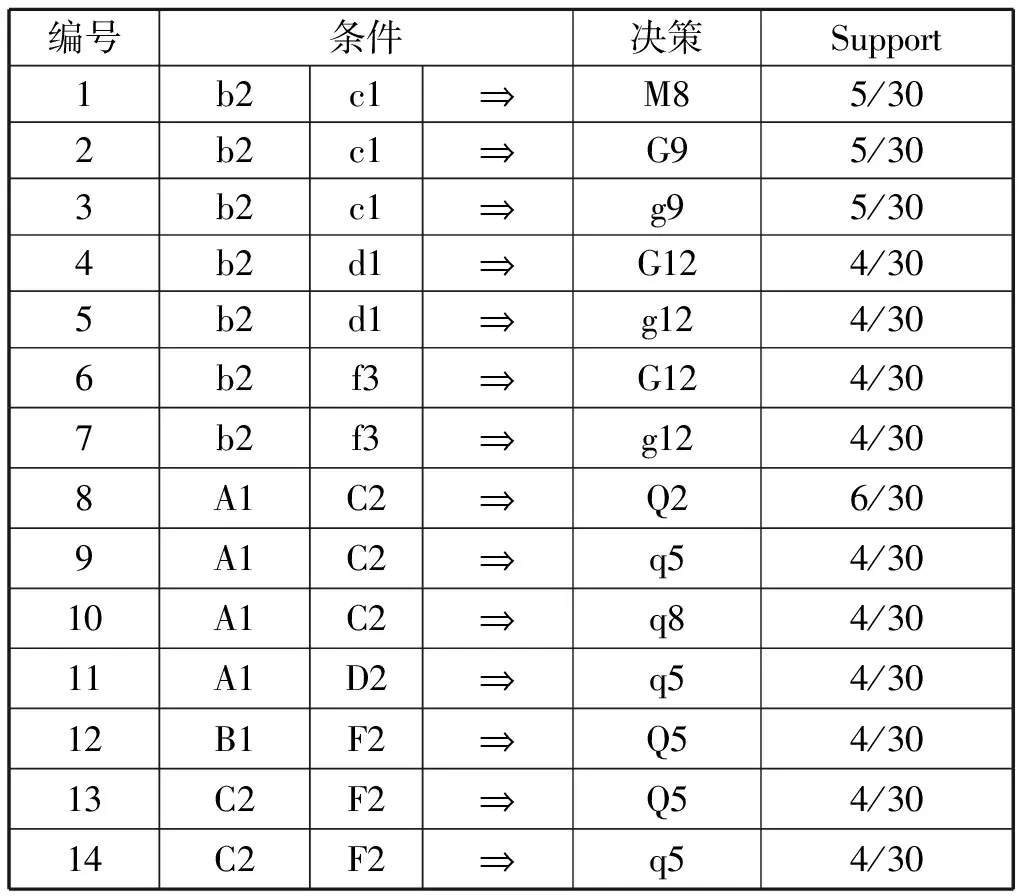
表3 與態勢匹配的關聯規則

根據3.2節沖突規則的消解方法，可以生成的決策為Q2(集群1：航母-護衛艦為主)、q5(集群2：驅逐艦-護衛艦為主)、G9(集群1發射導彈數量：9枚)、g9(集群2發射導彈數量：9枚)、M8(攻擊目標：驅逐艦-驅逐艦)。將生成的決策替換歷史案例16的決策，案例調整完成，調整前后的結果對比如表4所示。對比測試案例③，經過調整后的決策方案和測試案例的決策方案非常接近，證明此方法對編隊作戰案例調整有效。

表4 案例調整前后對比

最后將調整后的案例用于實際決策，指揮決策內容如表5所示。表中的海區和各階段時刻需要根據實際情況制定。

表5 編隊作戰決策

4.2 案例調整精度分析

為了衡量本文方法的調整精度，引入平均絕對誤差百分比(MAPE)，計算數值型數據的調整精度:

(7)

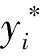
針對非數值型數據，定義如下計算精度的公式：

(8)

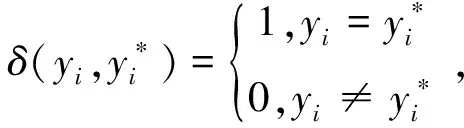
總體調整精度公式：

(9)

由上述5個測試案例，再利用本文所提的案例調整方法和調整精度公式繪制了5個測試案例的調整精度圖，如圖3所示。由圖3可知，案例的調整精度可以保持在0.8左右，調整精度相對較高。

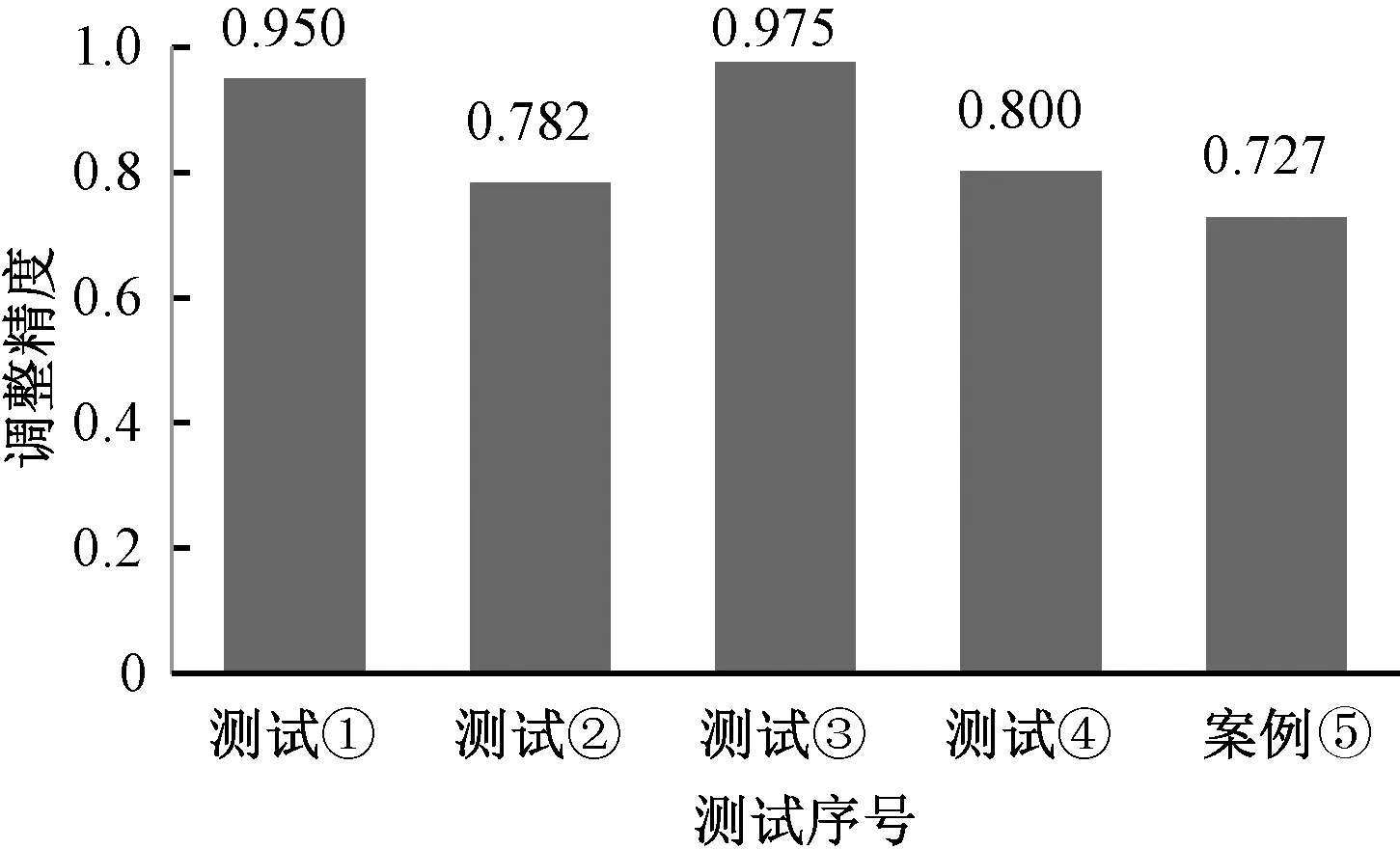
圖3 調整精度

5 結束語

本文采用多值關聯規則的方法挖掘編隊作戰案例中的潛在知識，用關聯規則去調整案例，并解決了案例調整時的規則沖突問題，保證了案例調整精度。通過仿真實驗，證明該方法對海上編隊作戰案例的調整有效。如果經過案例調整后的決策還不能滿足指揮員的要求，那就需要指揮員憑借自身作戰經驗進行調整，制定決策。